“一题多解”与初中数学核心素养培养

曾昭党

(福建省三明市尤溪县第五中学,福建 三明 365100)

传统教学注重对基础概念、常规解题方法的讲解,意在让学生掌握解题套路,从而应对相关数学题目.然而,初中数学题千变万化,若学生长期处于被动学习的状态,使用一成不变的套路解题,势必会影响学生逻辑推理、数学抽象、数学建模等核心素养的提高.教师应该认识到一题多解教学的必要性,并采取针对性的教学措施在一题多解教学中有效渗透核心素养,在活跃学生解题思维的同时,提高学生的数学解题能力.

1 概念界定

1.1 一题多解

一题多解指的是呈现问题后,学生使用不同的方法解决问题,通过从不同的视角分析问题,培养学生发散思维与创新思维.在教学中,一题多解与一题多变教学存在深入关联,通过问题变式、问题关联等方式揭示数学概念、数学算理、数学算法的本质属性与非本质属性,从而提升学生的学习层次,开拓学生的解题思路[1].

1.2 数学核心素养

数学核心素养指的是学生在数学学习过程中应具备的关键能力,包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六项内容.其中,数学抽象指的是能够透过数学事物的表面属性总结出一般规律,并使用数学语言将其表达出来[2].逻辑推理指的是能够根据数学事实、数学命题按照具体的逻辑规则完成证明命题为真(或假)的能力.数学建模指的是应用数学语言、数学知识、数学方法构建数学模型并解决问题的一种能力,包括分析问题、模型构建等.直观想象指的是基于几何直观、空间想象的基础上联想数学事物的形态、变化过程的一种能力,包括图形描述、数形转化等.数学运算指的是基于明确的运算题目,按照具体的运算法则完成题目解析的能力,包括运算理解、运算应用等.数据分析指的是基于统计的相关知识分析、推理数据信息,并形成新的结论的一种能力,包括数据收集、数据整理等.

2 基于“一题多解”培养数学核心素养的策略

2.1 设计融合教学目标,奠定素养培养基础

教学目标是对课堂教学的预设,对组织教学活动、衔接教学环节、填充教学内容具有指导意义.实际教学中,教师根据数学学科核心素养的教学要求融入一题多解的教学过程中,将两项教学目标融合,设计综合性的教学目标,为推动一题多解教学顺利进行和强化核心素养渗透奠定基础.目标设计过程中,教师需结合学生的最近发展区设计符合其学习需求的目标,确保教学目标发挥其导向作用[3].

以 “有理数的加减混合运算”这节课的教学为例,首先,教师分析教学目标:①了解代数和的概念;②理解有理数加减法可以相互转化,会进行加减混合运算;③渗透化归与转化思想.然后,教师挖掘解题目标中蕴藏的一题多解教学元素,同时找准教学目标与核心素养培养要求的契合点,如与运算素养、逻辑推理素养、数学抽象素养的契合点等.找准契合点后,教师再融合教学目标,预设一题多解教学思路与教学效果:①布置简单计算习题,让学生从有理数加的角度、有理数减的角度分别计算习题答案,激发学生的多解意识,并提升学生的数学运算素养;②布置有理数加减混合运算的应用题,让学生在解题时提炼有理数信息,并通过不同方式解决问题,使学生掌握多种解法的同时,形成良好的逻辑推理与数据分析素养.教师根据教学目标、教学设计有序组织解题教学活动,能够进一步提高一题多解的教学效率.

上述案例,通过融合解题教学目标、核心素养培养目标找准一题多解的教学方向,并根据融合目标搭建教学框架,实现了一题多解教学与素养教学融合发展的教学目标,奠定了习题教学顺利展开的基础.

2.2 围绕问题发散讨论,培养学生的逻辑推理素养

初中数学教学过程中,要使学生具备一题多解的能力,首先要解决传统灌输式教学造成的学生思维单向、思维僵化问题.针对某一类型题目展开一题多解教学时,教师首先要革新教学观念,将学生作为习题教学的主体,鼓励其围绕问题提出问题,主动与教师、其他学生展开讨论.通过组织师生互动、生生互动等多种讨论活动,在课堂上发散学生的思维,使其学会从不同角度分析、推理数学问题,在培养学生逻辑推理素养的同时活跃其解题思维.

以 “平行线的性质”一课的解题教学为例,完成基础知识点的教学后,教师呈现例题:如图1,已知CD是∠ACB的平分线,DE∥BC,∠B=70°,∠ACB=50°,求∠ADE、∠DEC、∠EDC三个角的度数.这一题目要求∠ADE、∠DEC、∠EDC的度数,需要学生从不同角度分析这一题目,形成不同的解题思路.对此,教师可组织生生讨论活动,让学生以小组为单位结合已掌握知识点、已知信息确定解题思路.比如,有学生结合“两直线平行,同位角相等”的概念确定图中∠ADE的度数,解出∠ADE=70°的答案.讨论时,学生通过提出自己的见解给其他学生启发,使学生联想两直线平行,同旁内角互补;两直线平行,内错角相等的知识,并从不同角度进行推理,确定解题思路.

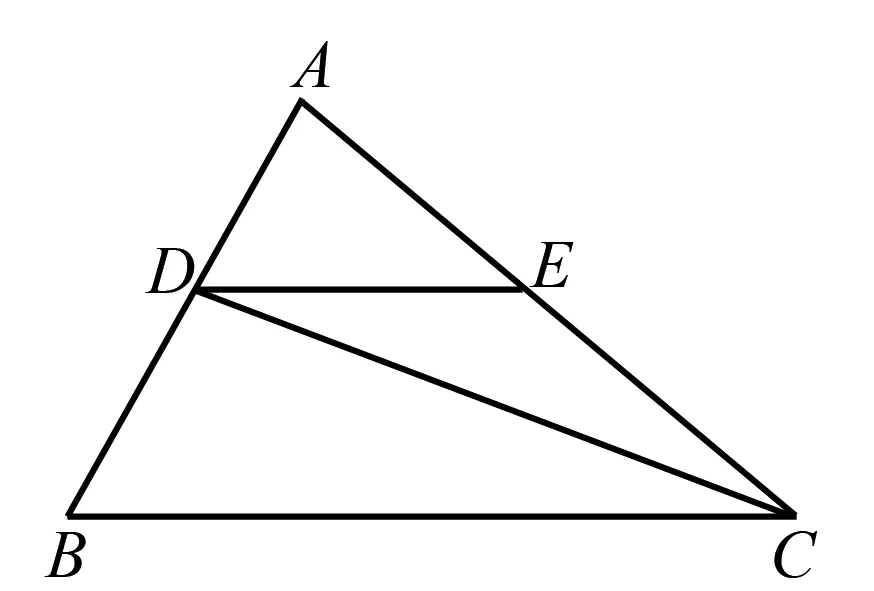
图1 例题用图

上述案例,教师围绕典型例题组织生生讨论活动,让学生结合已掌握的知识点提出看法,以抛砖引玉的形式启发学生的一题多解思维,在广泛交流、深度思考的过程中发散学生的解题思维,提升学生的逻辑推理素养.

2.3 围绕问题对比分析,培养学生的数学抽象素养

一题多解的教学目的并非“多解”,而在于培养学生多角度、多层次、多方位思考问题、探究问题的解题思维.教师在展开一题多解教学时,应拓宽教学思路,将围绕着某一题目的多种解法教学转向类型题的分析教学,使学生明确不同题目的异同处,题目中条件与结论的内在关联,使学生掌握从不同角度探究问题的方法[4].对此,教师有必要在解题教学中进行对比分析教学,使学生在题目对比的过程中总结规律,进一步培养学生的数学抽象素养.

上述案例,教师结合教学内容的考点呈现多种类型题,让学生通过对比分析探究解题本质,既提升了学生解题思维的灵活性,又提升了学生的抽象素养.

2.4 围绕例题展开变式,培养学生的数学运算素养

要真正摆脱解题方法单一的问题,使学生能够全面的、多角度地探究数学问题,需要教师围绕典型例题展开变式教学.在学生掌握问题的常规解法后,组织学生从其他角度探索问题的解决方法,使学生认识到问题解法的不唯一性,增强其灵活应变的解题意识.基于此,教师再出示类型变式题,让学生在读题、解题、运算的过程中总结一题多解的经验,同时提升其数学运算素养.

2.5 应用导图总结方法,培养学生的数学直观素养

思维导图是一种直观、有效的思维教学工具,将其应用到初中数学的一题多解教学,可以使学生的解题思维更加清晰、直观,有助于在解题教学中培养学生的数学直观素养.应用导图时,教师可将待解决的数学题目作为导图的锚点,围绕问题搭建多解框架,组织学生将不同解题思路填充到思维导图的结构框图上,并总结这一方法的优缺点[5].这样,学生能够充分掌握题目的不同解法,一题多解的能力得到增强.

以“一元二次方程的应用”一课的教学为例,教师出示典型例题:制造一种产品,原来每件的成本是120元,由于连续两次降低成本,现在成本为78元,求平均每次降低成本百分之几?围绕这一问题设计思维导图,让学生将题目的已知量与未知量、列方程解应用题的步骤、解方程的方法(配方法、公式法、因式分解法)等内容填充到思维导图上.借助思维导图直观呈现不同解题方法及其解题依据,进一步强化一题多解教学效果.

综上所述,初中数学一题多解教学与核心素养培养教学存在教学关联,融合两项教学工作对于提升初中学生的数学综合素养有着积极意义.实际教学中,教师应充分理解一题多解、数学核心素养的教学内涵,同时根据初中学生的认知发展规律采取多样化的解题教学方法,使学生在独立思考、综合讨论、对比分析的学习过程中形成灵活的解题思维,进一步提升学生的数学核心素养.