基于分类探讨思想的初中数学解题教学改革研究

徐 芳

(江苏省徐州市大屯矿区第二中学,江苏 徐州 221611)

进入二十一世纪以来,随着新课程标准的出台及实施,国家对基础教育教学工作提出了更高的要求,尤其对数学而言.由于数学是与科学发展息息相关的学科,在初中数学的解题教学中,不仅要教给学生解题的方法与技巧,更要教给学生问题的解决思路,从而习得推理思维以及能力[1].在这样的学习环境下,强化对基于分类探讨思想的初中数学解题教学研究尤为重要且迫切.

1 分类探讨思想应用于初中数学解题教学的必要性及原则

1.1 分类探讨思想应用于初中数学解题教学的必要性

分类探讨思想是初中阶段最重要的数学思维方法之一,也是近年来中考的重点以及热点.它要求教师循序渐进地引导教学,认真总结、启发以及揭示分类探讨的本质.目前,分类探讨的思想已经成为一种非常重要的数学思想,它不仅是一种独特的数理逻辑方法,而且是一种有效的解题策略.由于分类探讨具有综合考虑各种问题的逻辑优势,对培养学生的学习能力,提升学生的思维严谨性起到了很好的作用[2].在回答一道数学题时,假设题意存在一系列不确定因素,无法解出,则可以将问题分解为几个小问题,进行分类探讨.因此,在初中数学教学实践中,教师应基于分类探讨思想,逐步深入培养学生的数学思维,以进一步提升学生的思维能力,使学生养成良好习惯,这符合新课标的要求.

1.2 分类探讨思想应用于初中数学解题教学的原则

在解决初中数学问题时,分类探讨思想的运用必须符合相关原则,才能充分发挥分类探讨思想的作用,提升学生学习的有效性.在运用分类探讨思想进行初中数学教学过程中,教师应该有必要详细了解学生的学习状况,引导学生将思路运用到问题的解决中.此外,还要充分关注学生的学习过程,将日常生活与数学问题巧妙地结合起来,帮助学生理解数学知识.用栩栩如生的内容提出数学问题更有可能影响学生[3].另外,在运用分类探讨思想时,教师要能够以教学内容为主要媒介,将其与各个教学环节的特点联系起来,进而将分类探讨思想融入各个环节[4].以科学的方式,学生可以理解及吸收这种解决问题的思想.教师还应能有效地引导学生,使学生充分关注与自问相关的问题,使学生在分类探讨思想中真正掌握解决问题的方法.在新时期,在将分类探讨思想应用于初中数学教学实践中,教师应当对这些原则给予充分的重视,确保教学实施的效率与效益.

2 分类探讨思想应用于初中数学解题教学的步骤

为了在初中数学教学中有效运用分类探讨思想,必须按照科学的步骤来实施.在教学中,必须根据相同的度量来分析每个类别,并且必须避免重复和遗漏.在分类探讨过程中,探讨要系统、全面,每一步主要是根据研究目标,分类分析探讨详细结果.在初中数学解题教学过程中,分类探讨的实施要与主题要求一致,能够有效界定探讨的目的,然后进行实施探讨.在探讨一系列相对复杂的数学问题的过程中,需要对问题进行详细的分析,并具备将状况融入任何探讨的能力.然后,总结探讨的结果,以便从探讨中得出结论.

3 基于分类探讨思想的初中数学解题教学实践

3.1 初中数学解题中的分类探讨思想方法

在解决中学数学问题的过程中运用分类探讨的思想时,教师要能够根据实际教学状况进行指导,充分发挥这种方法的优点,使复杂的问题得以简化.通过有效运用分类探讨思维方法,可以有效提升学生学习数学知识的有效性,有效发展学生的数学思维及逻辑能力.其中,需要特别注意的是,分类探讨思路的运用要侧重于方法的科学性,使学生对数学定理、公式以及概念有一个全面的了解,以得到一个有效解决方法.教师要能够考虑不同的教学情境,用分类探讨思想是学生紧张的心理活动的过程,这就要求能够找到可能的情境来一一证明,而不是解决问题.管理中的头脑风暴法可以使学生在有限的时间内找到实际问题的解决方案,教师可以提出具体而多样的数学题目以及头脑风暴,使学生能够有效地将分类思想应用到解题中.总而言之,在应用这种方法的过程中,要侧重于学生的主体性,在此基础上开展教学活动,旨在获得良好的教学效果.

3.2 基于分类探讨思想的初中数学解题教学实践

3.2.1 在解方程中运用分类讨论思想

由于数学概念的限制引起的分类探讨.例如,方程是中学数学中常见的内容,不少学生在学习一元二次方程后往往会存在思维定势的问题,懒于思考,从而降低了学习成绩.运用分类探讨的思路,可以很好地判断解方程的状况.因此,教师应着重教学生如何利用分类探讨来解决练习难题.

例1 已知关于x的方程kx2-2x-1=0有实数根,求k的取值范围是____.

解析为了更好地引导学生,使学生养成用分类探讨思想的习惯.将中学学过的方程总结为:一元一次方程、二元一次方程、分式方程和一元二次方程.从形式上看出它不是二元一次方程也不是分式方程,应该对k进行分类探讨.当k=0时,原方程是一元一次方程,方程有解;当k≠0时,是一个关于x的一元二次方程,若方程有实数解,则必须满足△=22+4k≥0所以k≥-1.分两种状况探讨,最终答案是k≥-1.诸多学生在解题过程只考虑他们最近学习的一元二次方程的情况,而忽略了探讨当k=0时方程是一元一次方程的情况,导致失分.

3.2.2 在几何问题中应用分类讨论思想

由于几何概念的性质,分类探讨思想在几何中有广泛的应用.

例2在等腰三角形中,有一个内角是50°,求其余内角的度数.

解析这是在教学中运用分类探讨思想解决几何问题的典型例子.其中50°既可以用作等腰三角形的顶角,也可以用作等腰三角形的底角.

在讲解求三角形边长的时候,使用分类探讨的思想也是有用的.

例3当一个直角三角形有两条边长分别为3和4,求第三边的长.

另外,分类探讨也可以解决由于图的不确定性引发的问题.

例4 已知△ABC中,AB=AC,CD是AB边上的高,且AB=2CD,则∠ABC=____.

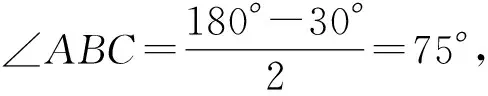
图1 例4题图

图2 例4题图

3.2.3 克服初中生对分类讨论思想的学习障碍

对于诸多初中生而言,数学是初中课程中比较薄弱的一门学科,很容易对分类探讨的思想理解不透彻,导致解题时出现不必要的失分.这也导致学生对数学学习缺乏信心.为了更好地应对这种状况,教师应在课堂上营造良好的氛围,充分发挥学生的主观能动性,将所学知识系统地总结出来,使学生能学会运用分类探讨思想,并有效加以应用.

在中学数学中,几乎所有的知识点都与分类探讨的思想有关.基于此,应用时要让学生知道为什么分类,制定明确的分类标准,分析中学数学中可能出现的一系列因素,仔细分类,一一探讨,最后得出正确答案.在初中数学解题教学中,分类探讨是一个非常重要的数学思想,通过强化训练,可以培养学生严谨的思维,也可以增加学生学习数学的兴趣,提高学习效率.

综上所述,在初中数学教学中运用分类探讨思想,需要考虑不同的情况,才能成功解决问题.本研究系统性地分析了分类探讨思想应用于初中数学解题教学的必要性及原则,分类探讨思想应用于初中数学解题教学的步骤,并开展了基于分类探讨思想的初中数学解题教学实践.希望通过具体的理论研究以及案例分析,对提升初中数学解题教学水平起到积极的作用.