面向巷道环境的稀疏锚节点UWB定位方法

汪 亮，李宗林，石繁荣

(西南科技大学 信息工程学院，四川 绵阳 621010)

0 引言

依据国家安全监管总局制定的《金属非金属地下矿山安全避险“六大系统”安装使用和监督检查暂行规定》，井下人员定位系统是矿山安全避险的重要组成部分。针对智慧矿山建设，无线传感器网络、无线定位等技术正发挥重要作用。我国是资源消耗大国，尤其是对煤矿的开采与消耗更加明显[1]。但煤矿能源大部分存在于井下，使得其开采具有更大的难度[2]。由于井下巷道环境较为复杂，空间狭窄，不确定因素众多，使得矿井事故的发生具有不确定性，且其发生危险的可能性大大增加。因此需要对井下工作人员实时监控其位置信息，从而能够及时对遭遇矿井事故的人员展开高效、迅速、准确的救援任务[3]。井下巷道环境不同于地面，无线电信号的传输存在较多的干扰因素，尤其是非视距的影响，会使得定位精度降低，因此需要选择合适的无线通信技术和节点定位算法。

目前，随着无线传感器网络的快速发展，无线定位技术作为其主要技术之一，也被广泛应用于各个领域，其发展也越来越迅速，常用的井下定位技术[3-4]主要有ZigBee[5-6]、Wi-Fi[7-9]、射频识别(RFID)[10-11]、超宽带(UWB)[12-13]和蓝牙技术[14]。其中UWB技术具有抗干扰性强、定位精度高等优点可作为井下定位技术，而ZigBee技术具有低功耗、低成本、易于组网等特点可用于井下无线通信。基于测距的无线定位算法是目前高精度定位采用的主要技术[15]，主要有达时间(TOA)[16]、到达时间差(TDOA)[17]、到达角度(AOA)以及接收信号强度指示(RSSI)[18-19]，其中TOA和TDOA可用于UWB定位技术，但是TDOA算法需要满足基站设备间的时间同步，且其计算较为复杂，但TOA算法测量方法简单且容易实现，因此选择TOA作为井下定位算法。TOA定位算法通过记录型号的发送时间和接受时间来计算信号在两个设备间的传播时间，从而得到设备间的距离，再使用位置坐标计算方法来获得节点的位置坐标。常见的TOA测距算法有：单边双向测距算法和双边双向测距算法，这两种测距算法都解决了时间同步的问题，而常见的位置坐标计算方法有：三边测量法、极大似然估计法、三角计算法、Chan氏算法。

当前的节点定位都是依靠锚节点来进行定位的，现有的定位算法均表明，锚节点比例越高，定位的精度越高[20]，但是锚节点的增多会使无线传感器网络的成本增加，不利于节点的部署，而且井下不同于地面，需要单独测量锚节点的坐标，使得锚节点部署更加困难，因此如何在巷道中使用更少的锚节点获得精确的定位成为了本文的研究重点。本文在井下布置的节点较为稀疏[21-23]，其定位方案是：首先，利用巷道环境的特殊地形，使用两点定位；其次，本文提出了在锚节点上安装双测距模块的锚节点的方法，以获得不同的测距信息；最后，引入虚拟锚节点[24]，增加锚节点的密度，提高节点定位精度。

本文的后续章节如下，第一章节介绍了本文所使用的测距算法即双边双向测距，第二章介绍了本文所使用的位置坐标估计方法即三边测量法和极大似然估计法，第三章介绍了本文解决井下稀疏锚节点问题所使用的3种方法。

1 双边双向测距算法

DWM1000可实现TOA双边双向测距，其测距过程如图1所示，其中TX代表的是发送，RX代表的是接收。首先，标签节点广播poll包到整个网络，并记录时间T1；锚节点接收到poll包并记录时间T2，响应一段时间后再向标签节点发送resp包并记录时间T3；标签节点接收到resp包并记录时间T4，响应一段时间后再向锚节点发送final包并记录时间T5；锚节点收到final包，并记录时间T6。

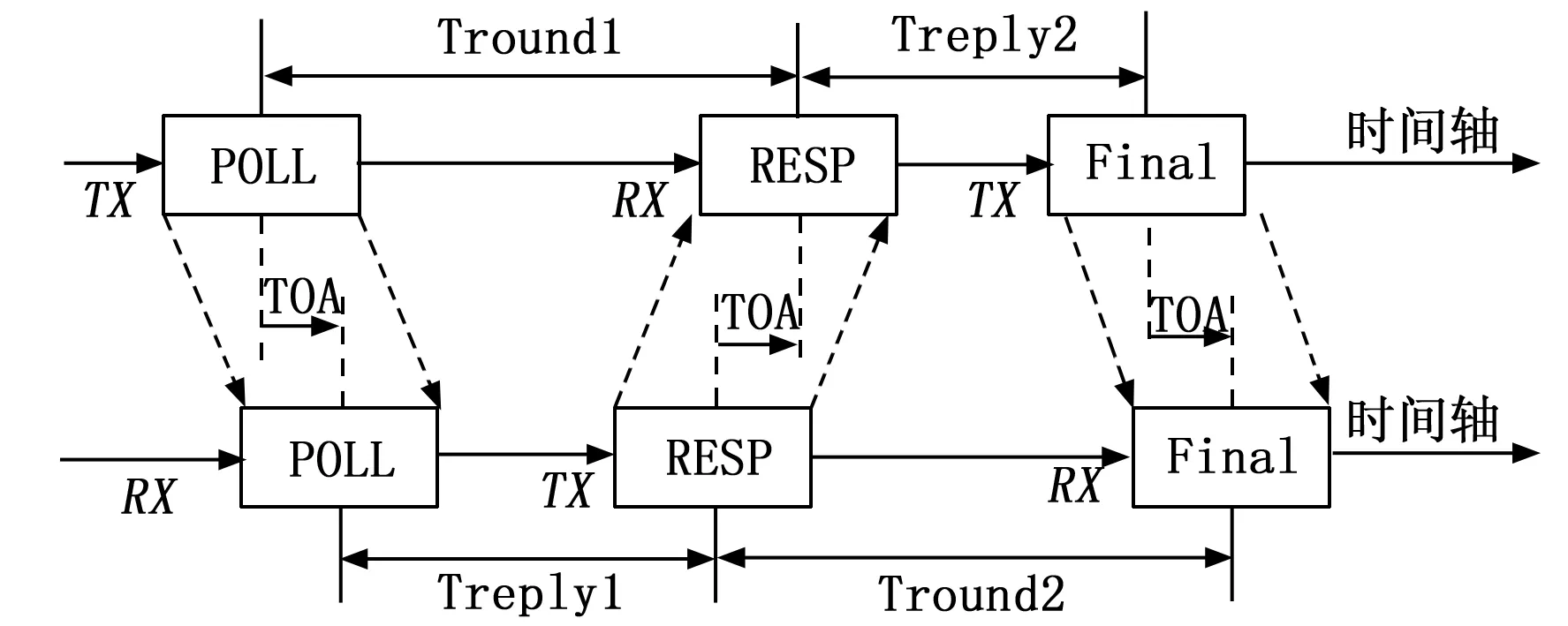
图1 双边双向测距方法

Tround1=T4-T1

(1)

Tround2=T6-T3

(2)

Treply1=T3-T2

(3)

Treply2=T5-T4

(4)

然后计算出节点间的传播时间为：

(5)

最后再将传播时间乘以光速可求出距离为：

d=Tprop·c

(6)

2 位置估计方法

2.1 三边测量法

三边测量法如图2所示，设未知节点D的坐标为(x，y)，已知锚节点A、B、C的位置坐标分别为A(xa，ya)、B(xb，yb)和C(xc，yc)，则未知节点D距离3个已知坐标信息的锚节点的长度可以表示出来，设它们的距离分别为da、db、dc，则存在以下公式：

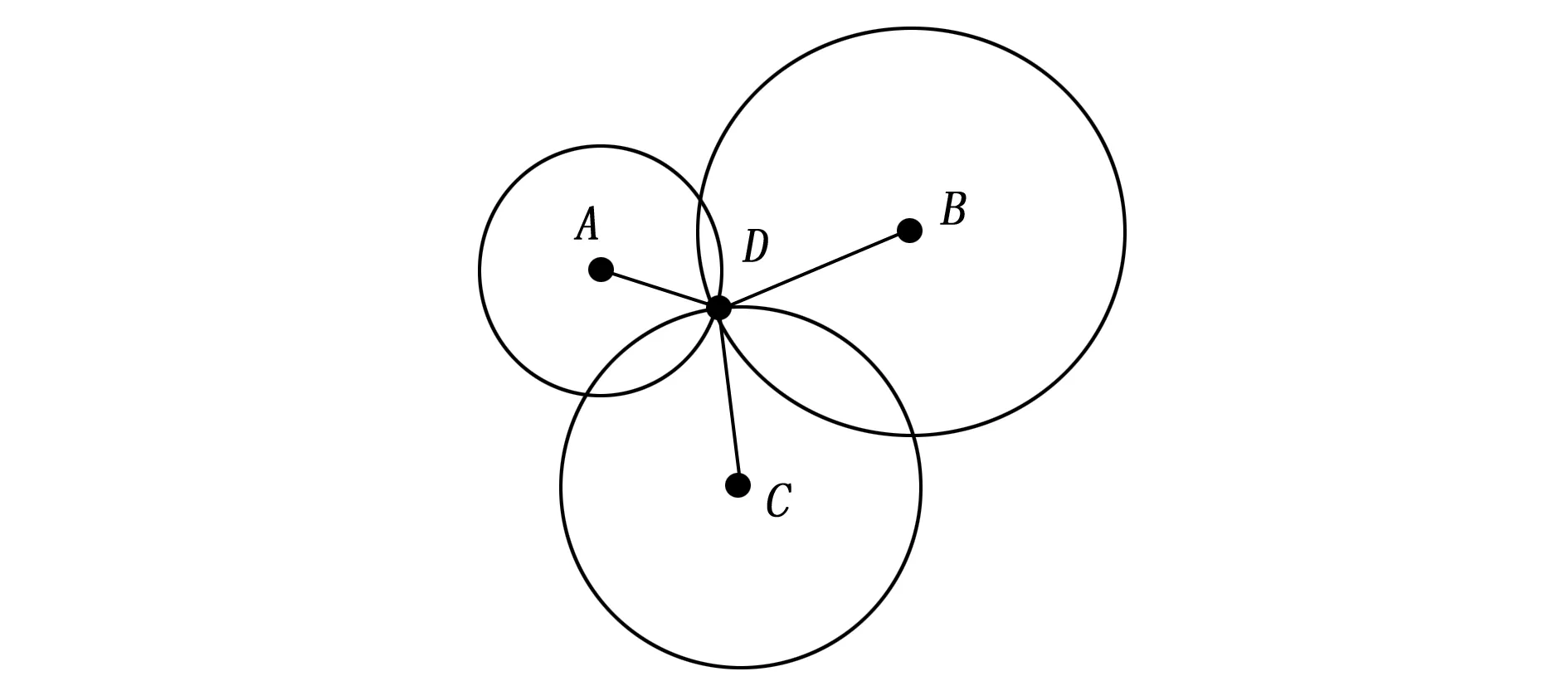
图2 三边测量法原理图

(7)

进一步推演出位置节点D的坐标信息，如下式所示：

(8)

为了便于计算，将坐标设置为(0，0)、(a，0)、(0，b)，距离分别为da、db、dc，可得待测节点D的坐标：

(9)

由式可知，x和y坐标都与距离的平方成正比，而x和y坐标的误差就与距离和距离的误差成正比。

2.2 极大似然估计法

极大似然估计法原理如图3所示，假定有一个未知节点的坐标为(x，y)，同时已知定位范围内的锚节点1，2，3，…，n的位置坐标分别为(x1，y1)，(x2，y2)，(X3，y3)，…，(xn，yn)，同时设未知节点距离这n个锚节点的长度分别为d1、d2、d3、…、dn，则可以得到以下公式：

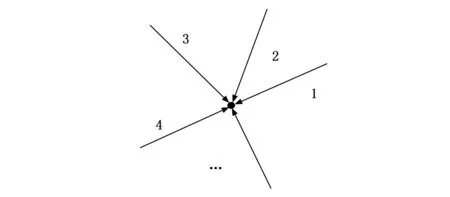
图3 极大似然估计法原理图

(10)

可以将上式转化成线性方程组AX=b的形式，其中有：

(11)

(12)

(13)

则待定位的未知节点的坐标可由标准最小均方差估计法进行计算得出：

X=(ATA)-1ATb

(14)

3 井下稀疏锚节点定位方法

图4介绍了本节的整体框架，以及巷道环境中，解决稀疏锚节点定位问题的3种方法，分别是：1)采用两点定位法；2)提出了锚节点上安装双测距模块的锚节点的方法；3)提出设置虚拟锚节点的方法。其中，稀疏锚节点是指锚节点的数量少且间隔比较远；虚拟锚节点是指位置固定且已被定位的标签节点，用来充当锚节点的作用。其总体流程是：在巷道中，由于所使用的锚节点比较少，很难准确地获得标签节点的位置信息。因此，可利用巷道的特殊环境使用锚节点上安装多个测距模块的锚节点，就可以获得多条测距信息，两个锚节点就可以获得3条及以上的测距信息，再采用两点定位法和三边测距法定位部分标签节点，其中一些位置固定的且已被定位的标签节点可以设置成虚拟锚节点，从而增加锚节点的密度，提高节点的定位率以及定位精度。虚拟锚节点与锚节点共同定位标签节点，如此循环，直到网络中所有的静态节点的位置坐标趋于稳定。

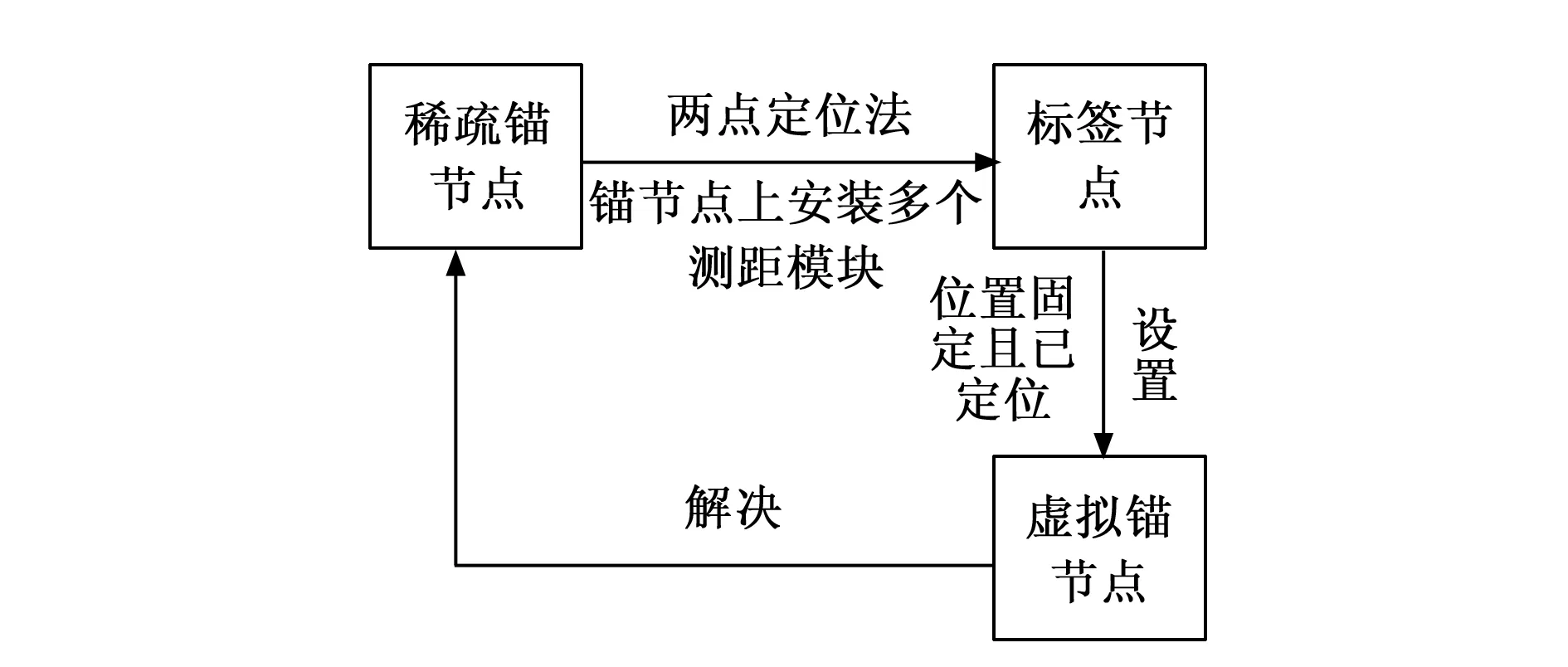
图4 整体框架

3.1 两点定位法

一般的定位算法至少需要3个锚节点与标签节点通信，才能获取标签节点的位置信息，但是井下巷道环境较为特殊，其环境不同于室内环境，在该环境中可以使用两点定位法来获取部分节点的坐标。两点定位法计算过程如下。

假设使用两点定位算法的基站坐标分别为(x1，y1)、(x2，y2)，未知节点坐标为(x，y)，未知节点到基站的距离为d1、d2。则距离方程组可获得下列公式：

(15)

对该公式求解可得出未知节点的坐标。

图5介绍两种情况下的两点定位，两条黑线表示巷道的两边，圆代表两种节点，其中白色表示锚节点，黑色表示标签节点。图5(a)表示将两个锚节点放置在巷道的一边，通过两点定位算法可以计算出两个坐标，然后将不满足条件的坐标舍去。图5(b)表示将锚节点放置在巷道的两边，可能出现两个位置，如果两个位置比较近，可取两个位置的中点表示该节点的估计位置，否则无法准确定位标签节点。

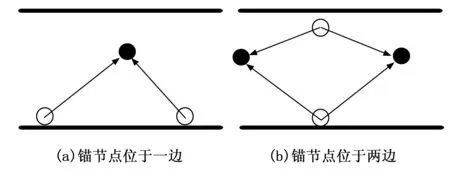
图5 两点定位法

3.2 锚节点上安装双测距模块的锚节点

一般的一个锚节点只能获得一条测距信息，但如果在锚节点上安装双测距模块时，可以获得两条测距信息，其中这两条测距模块之间的距离是固定不变且已知的，就可通过一个测距模块的位置信息来计算出另外一个测距模块的位置信息，那么安装了双测距模块的锚节点可以被看做两个锚节点，从而可以减少锚节点的人工部署数量。但是当标签节点距离锚节点越远，两条距离形成的角度也就越小，其误差可能会增大。

其中图6划分了该锚节点的两个通信范围即实线圈以内的范围和实线圈以外的虚线圈以内的范围。该图中，椭圆表示具有双测距模块的锚节点，标号为1和2的两个圆是两个测距模块，标号3是指标签节点，1和2之间的距离被叫做通信臂长。在第一个通信范围中，该锚节点可以获得两条测距信息；在第二个通信范围内，锚节点可以获得一条测距信息及一条方位信息，这条方位信息是确定标签节点在其虚直线的左边或者右边，那边测距模块所获得的距离小，可确定其标签节点在虚实线的那边。

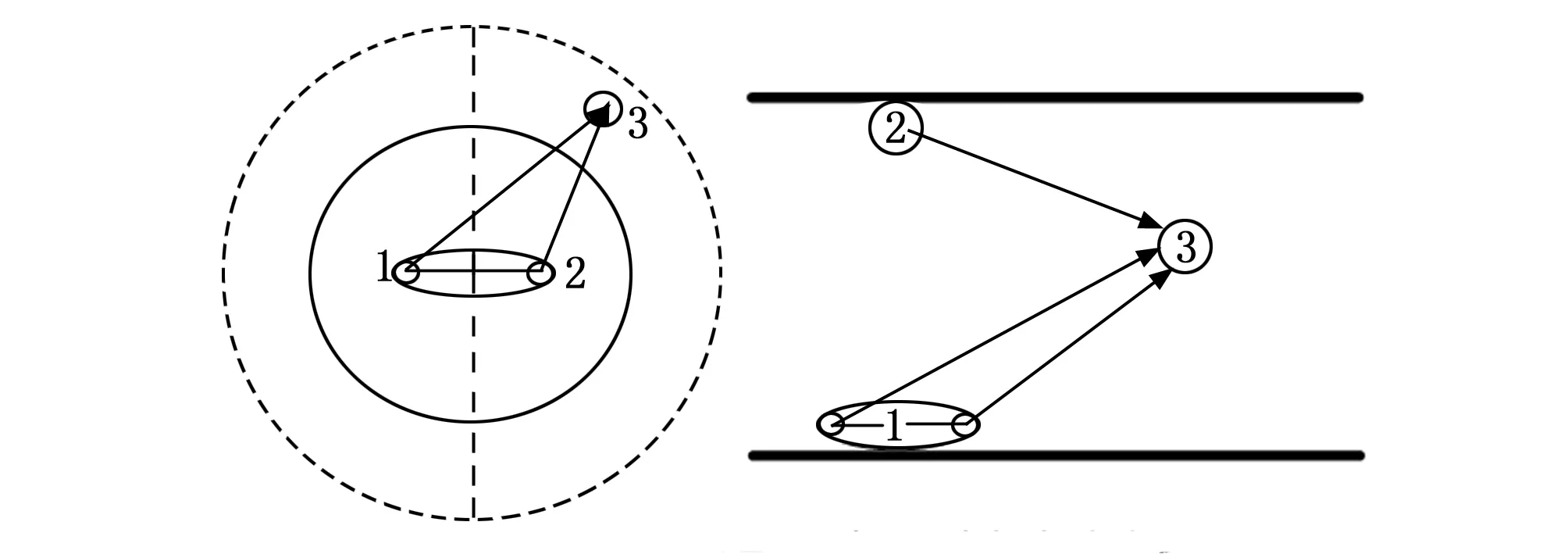
图6 锚节点通信范围 图7 两个锚节点定位

图6为两个锚节点定位标签，1号为具有双测距模块的锚节点，2号为普通锚节点，3号为标签节点，这两个锚节点可以获得三条测距信息或者两条测距信息以及一条方位信息，就可以使用三边测量法或者两点定位法计算出标签节点坐标，从而解决锚节点放置两边的问题。

3.3 设置虚拟锚节点

前两种方法虽然能解决一部分稀疏锚节点定位问题，但由于锚节点的密度比较小，其定位精度可能比较低，无法满足定位需求，这时就需要采用第三种方法。第三种方法将一部分标签节点设置成虚拟锚节点，让这部分节点充当锚节点的作用，从而可以相对增加锚节点的密度，进一步提高其定位精度。由于虚拟锚节点的位置信息是由锚节点估计获得的，其坐标本来就存在误差，让其定位其他标签节点时，会存在误差累积，导致误差增大，为降低误差累积的影响，因此需要选择定位精度高的部分标签节点作为虚拟锚节点。通过锚节点直接定位的一些标签节点，该类节点不存在累积误差，其定位精度较高，位置坐标较为准确，可直接作为虚拟锚节点。而通过锚节点和虚拟锚节点定位得到的标签节点就需要分析其定位误差，以及对后续标签节点定位的影响大小得的来决定是否成为虚拟锚节点。

图8介绍了井下的两种地方对虚拟锚节点的应用，一种是巷道，一种是房间。其中1号节点为锚节点，2号节点为虚拟锚节点，3号节点为标签节点。图8(a)表示的环境是井下巷道，在图8(a)中，3号标签节点无法直接被锚节点定位，但是2号节点在两个锚节点的范围内，可以获得该节点的位置信息，将其设置为虚拟锚节点，使用该虚拟锚节点与其中一个锚节点共同定位3号标签节点。图8(b)表示的环境是井下的房间，在图8(b)中，该房间体积大，锚节点布置得比较少，其中存在很多不确定的因素比如非视距等会影响定位效果，导致其定位精度较差，但是如何房间有一部分静止的标签节点，可以首先定位这些节点，并将其设置为虚拟锚节点，相对增加已知节点的密度，降低干扰因素的影响，从而进一步提高定位精度。

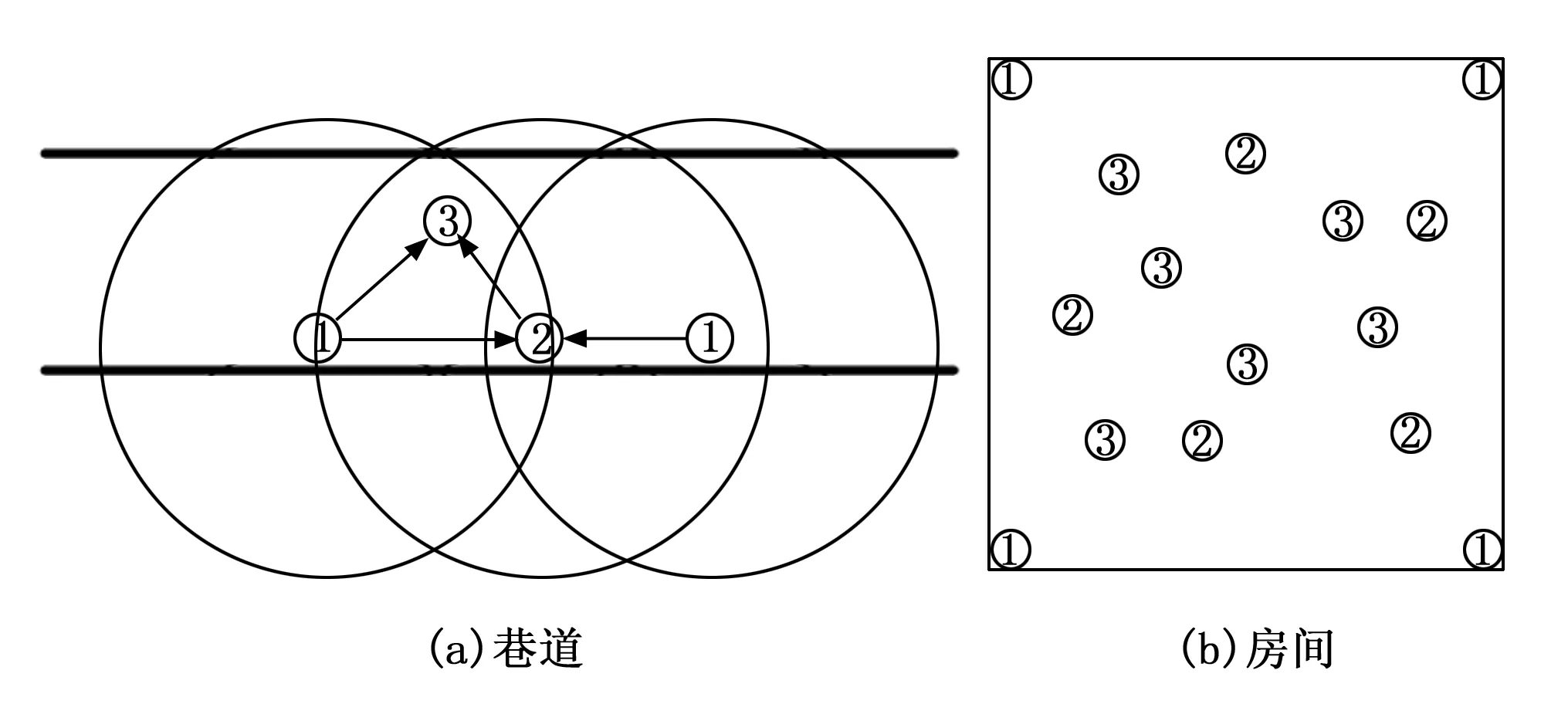
图8 虚拟锚节点的应用

4 实验与仿真

4.1 安装双测距模块的锚节点测距

锚节点的通信臂长是指具有双测距模块的锚节点中两个测距模块之间的距离。当锚节点的通信臂长分别为1 m和2 m时，其误差与测距距离的关系以及误差的累计分布函数见图9和图10，其中图9和图10中左边的图是第一个测距模块，右边的图是第二个测距模块。从图9和图10的第一个和第二个子图可以看出测距误差可以控制在0.2 m左右，这表明一个锚节点上的两个测距模块的测距误差在正常范围内，即执行测距任务时两个测距模块之间不会相互影响。图9和图10中的第三个到第四个子图展示了测距误差的累计分布函数，可以看出其误差主要集中在0.2 m以内。从这些图中也可分析出具有双测距模块的锚节点上的测距模块之间基本不会影响彼此的测距。

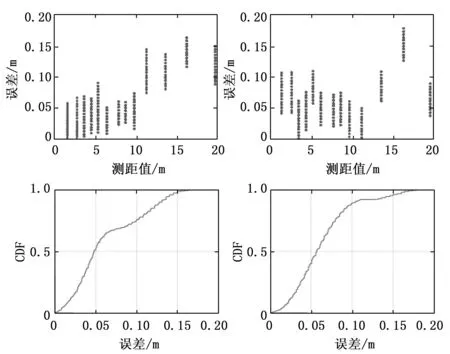
图9 通信臂长1 m

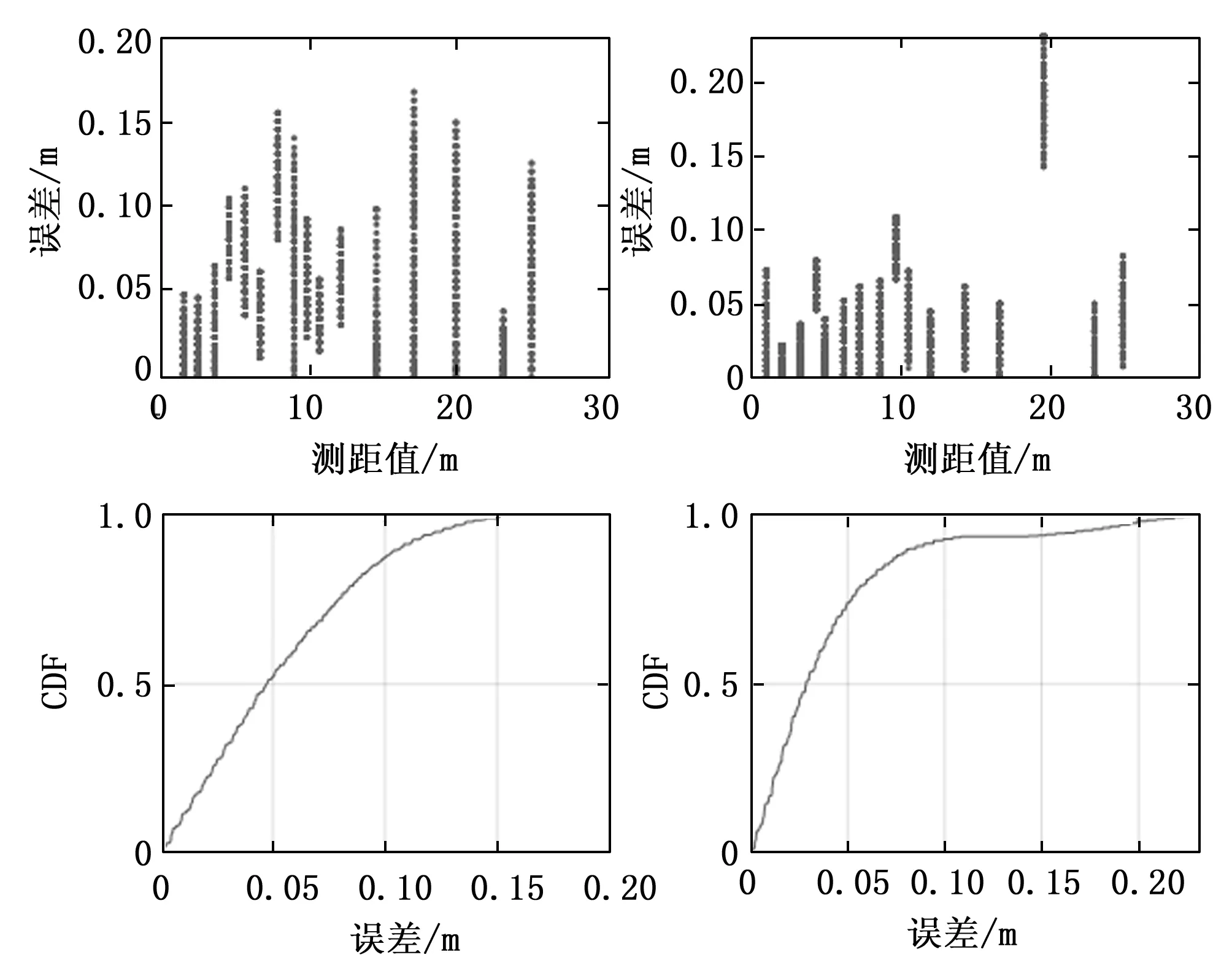
图10 通信臂长2 m

4.2 三边测量法

三边测量法计算简单，容易实现，但是，由于其只能够使用三条测距信息，使得其他的测距信息无法使用，导致其精度不是太高，该方法对测距要求也较高，测距误差较大可能导致其定位精度太低，该算法的好处是不需要太多的锚节点，锚节点的个数只需要满足3个即可。图11展示了锚节点放置不同的位置，定位误差随着标签节点位置的变化而变化的情况。从图中可以看出，定位误差一般是随着第一个锚节点与待测节点间的距离增大而增大，而且锚节点所放的位置不同其定位误差也是不一样的，一般在定位范围内的两个锚节点所处的距离越远，测距误差影响就越小，使得定位误差也越小，在锚节点所围成区域范围内，其定位误差能在0.5 m左右。

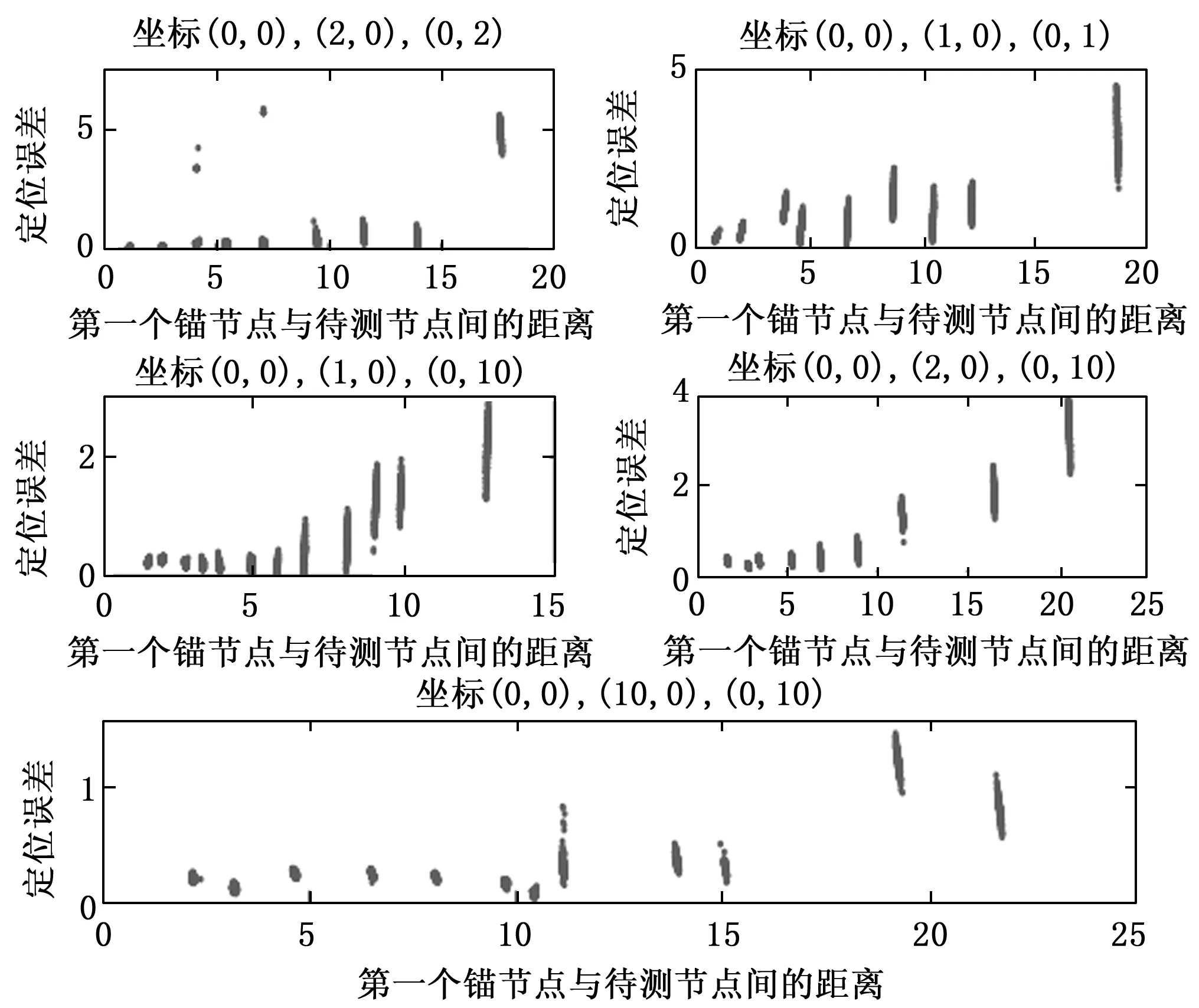
图11 三边测量法

4.3 极大似然估计法

极大似然估计的好处是可以利用更多的测距信息，在锚节点个数多的时候，精度相对较好，当只有3个锚节点参与定位时，其计算结果和三边测量法是一样的。由于极大似然估计法是通过矩阵计算得出的，当锚节点较多时，该方法计算较为复杂，单片机不易实现，图12为极大似然估计法的误差图，该图所使用的锚节点个数为4个，锚节点坐标分别(0，0)、(10，0)、(0，10)、(10，10)，从图中可以看出，该方法的定位误差可以控制在0.3 m左右，当其在锚节点所围成区域范围内时，大部分误差可以控制在0.2左右，而且该方法的定位误差跳动较小，其误差分布较为均匀。

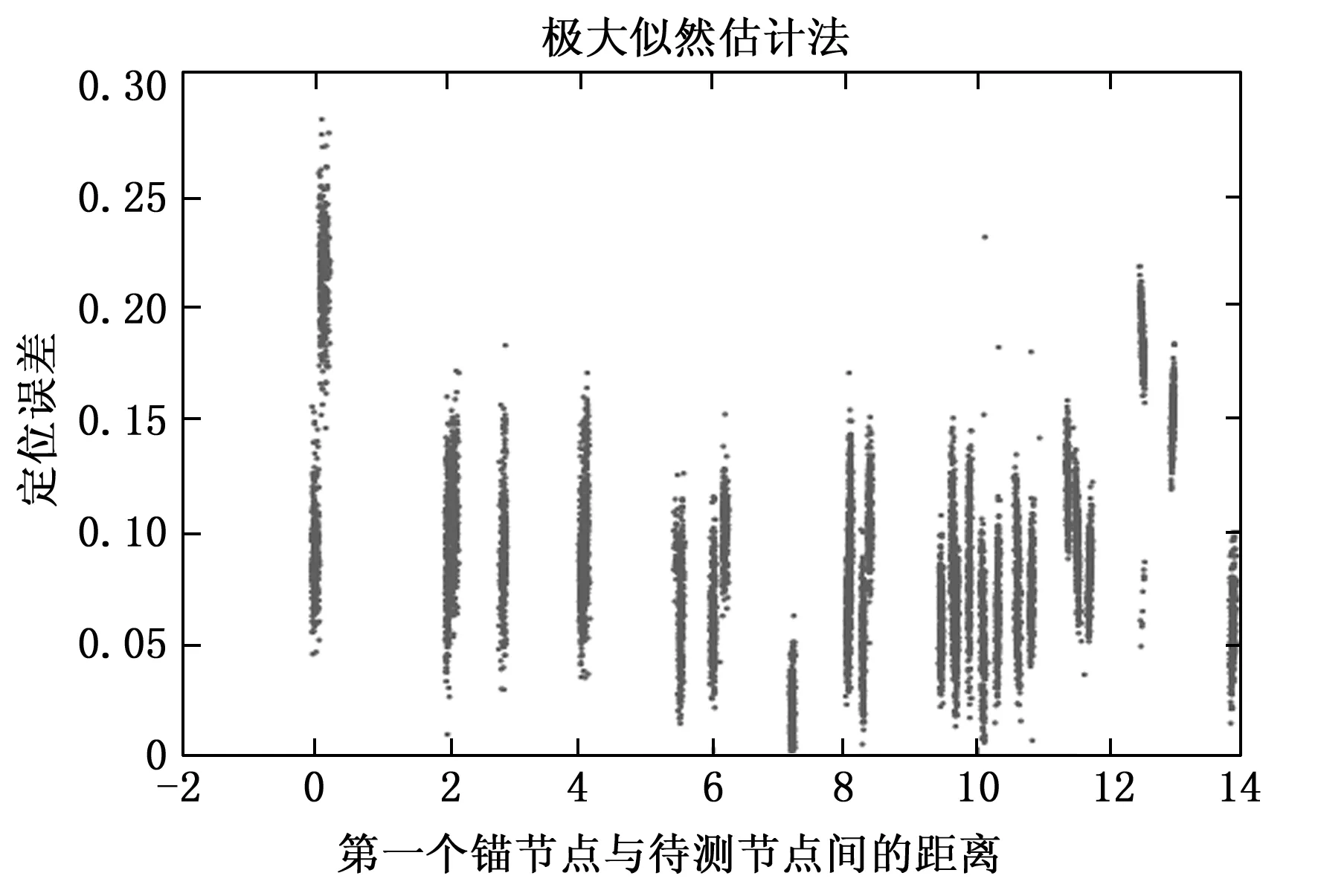
图12 极大似然估计法

4.4 运动轨迹

图13为标签节点沿着锚节点所围成的圈进行移动了两圈，锚节点的坐标分别(0，0)、(10，0)、(0，10)、(10，10)，由于移动过程中，标签节点与实际路径本来就存在偏差，使得其定位过程中的偏差相较于静止的时候会更大，但从图中可以看出，该标签节点在移动过程中的轨迹是连续的，其轨迹不会出现断断续续的，也能大致了解该节点的实际路径。

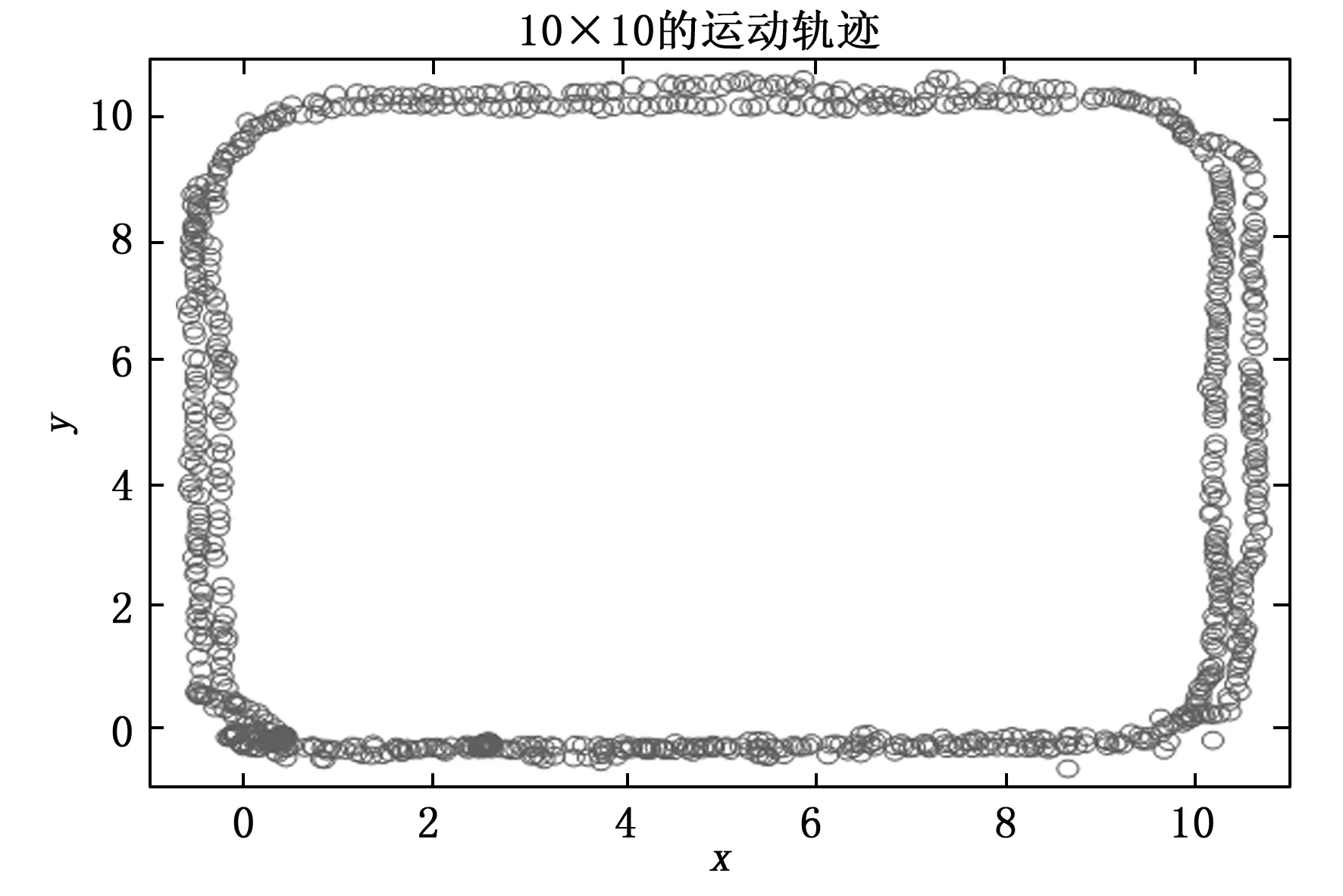
图13 10×10运动轨迹

4.5 具有双测距模块的锚节点定位实验

图14～图17为具有双测距模块的锚节点与普通的锚节点来定位标签恶点，这些图主要是锚节点的位置放置的不同，该写图中横轴和纵轴分别表示标签节点的横纵坐标值。由于4.1节已经得出具有双测距模块的锚节点的通信臂长与测距误差没关系。因此这些图是为了得出具有双测距模块的锚节点的通信臂长与定位误差的关系其中图14和图15中的锚节点通信臂长为1 m，图15和图17中的锚节点通信臂长为2 m。从图中可以看出，具有双测距模块的锚节点的通信臂长越长，其定位误差相对越小，而且锚节点间的距离越大其误差相对也越小，距离其锚节点所围区域的中心越远其误差一般也越大。从这些图中还可以看出，锚节点所围成的形状也会影响定位精度。

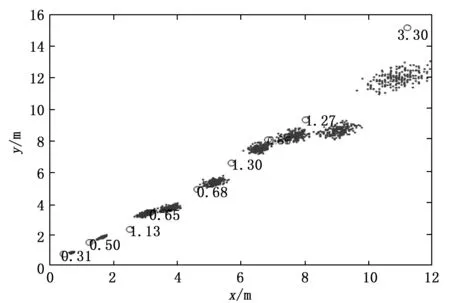
图14 测距模块坐标(0，0)(1，0)(0，1)

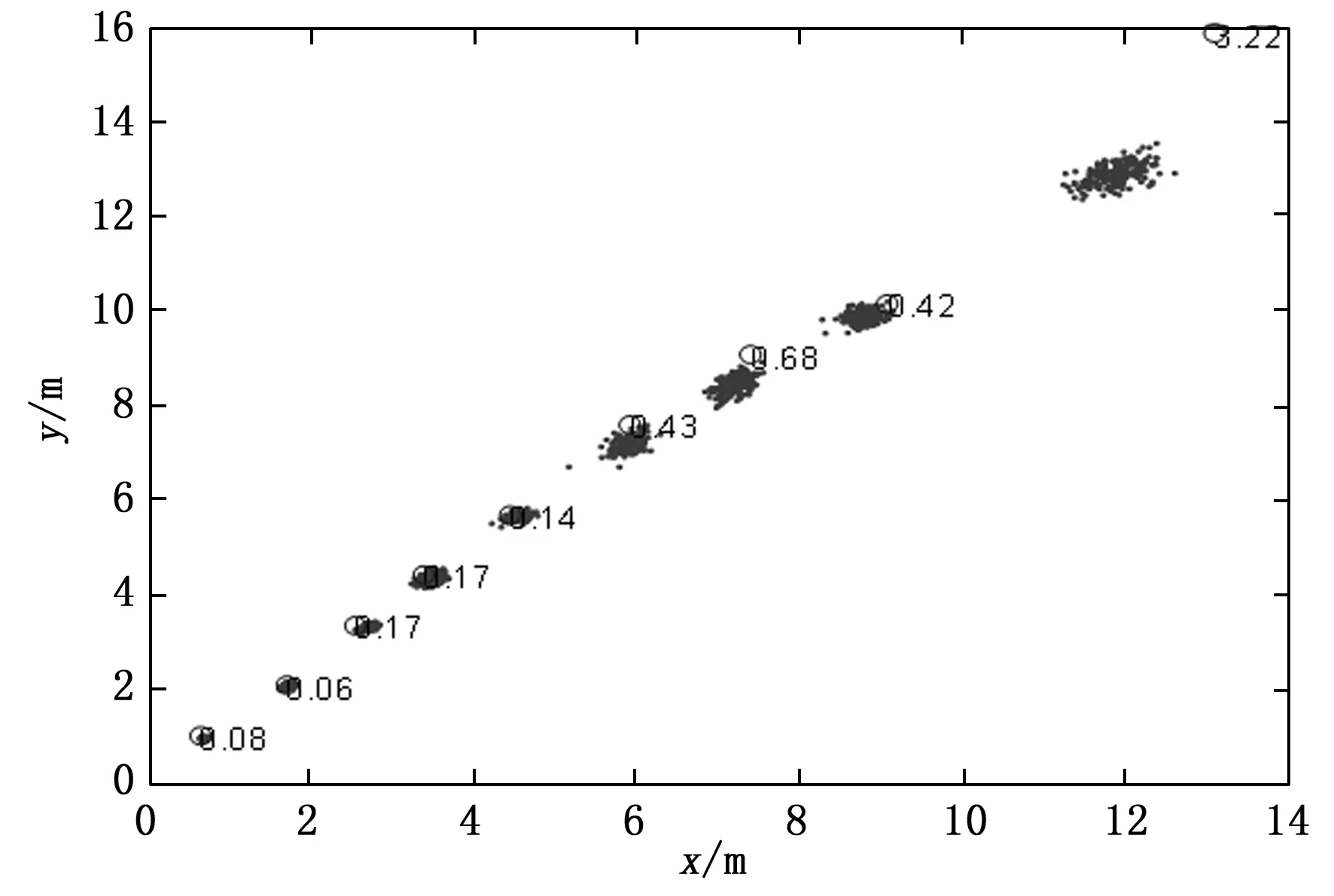
图15 测距模块坐标(0，0)(2，0)(0，2)

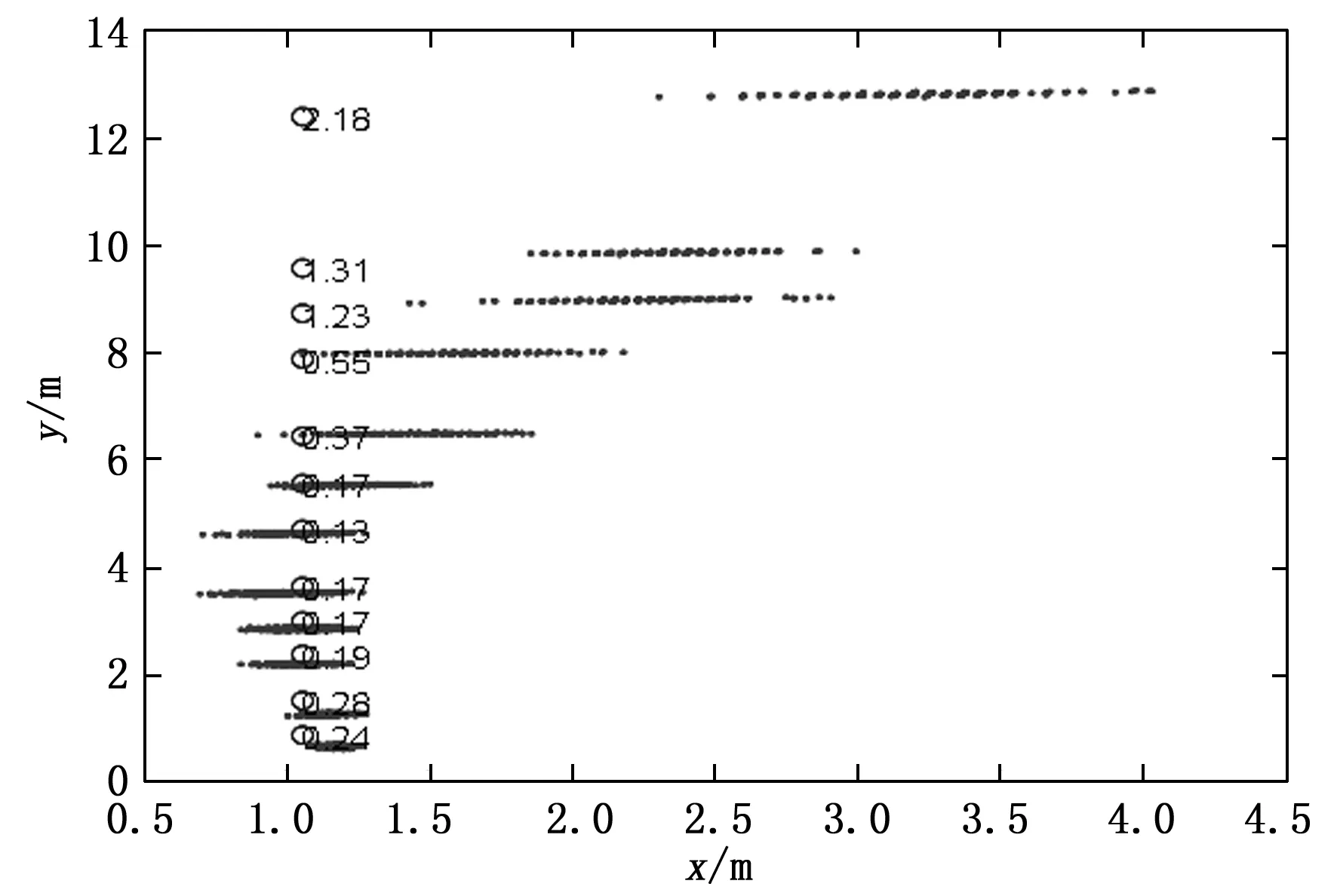
图16 测距模块坐标(0，0)(1，0)(0，10)

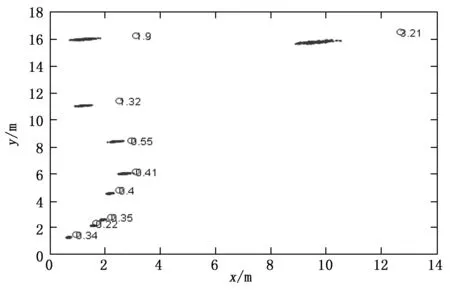
图17 测距模块坐标(0，0)(2，0)(0，10)

5 结束语

针对井下巷道的复杂环境，本文提出了稀疏锚节点情况下定位标签节点的解决方法，主要有3种：使用两点定位法和设计锚节点上安装双测距模块的锚节点测距的方法，最后再提出了引入虚拟锚节点的方法。通过分析及实验仿真可得出，这3种方法能够在锚节点稀疏时有效地提高节点的定位率以及定位精度，后续还需要进一步讨论来提高节点定位精度。