FPGA中基于空间连续性的碎片度量及任务放置

饶 广，饶云波

(1.内江职业技术学院，四川 内江 641000；2.电子科技大学 信息与软件工程学院，成都 610054)

0 引言

现场可编程门阵列(FPGA，field-programmable gate array)通常是部分可重构的，允许在运行时对芯片的各个部分进行配置，其中每部分可以执行一个独立的任务[1-2]。具有这种特性的设备可以同时容纳多个应用，其中每个应用可以由多个任务构成。要充分利用部分可重构结构的优势，就必须充分利用芯片资源[3-6]。不合理放置到达任务会导致芯片区域的一些部分浪费，因为这些部分尽管是空闲的，但它们太小而无法容纳另一个到达的任务。通常把这些空闲的较小部分称为碎片，类似于传统存储系统中的碎片，这些碎片可能占芯片区域的很大比例[7]。因此，区域碎片是获得良好的芯片资源利用的最大障碍之一。一方面，高区域碎片化表示芯片上占用部分的分散，因此可能导致低的芯片利用率；另一方面，低区域碎片化使得到达任务能够被放置，从而提高芯片利用率。

在一个在线放置系统中，由于矩形任务的动态添加和删除，使得FPGA的空区域变得高度碎片化，因而无法有效地利用FPGA区域。一个高度碎片化的芯片是指其中包含了大量的由一些被占用单元所分割形成的孔洞[8]，即任务矩形边界以外的区域资源的碎片。如果一个任务的矩形区域没有可用的足够的相邻资源，则该任务可能被拒绝放置。图1所示为这样的一个例子，其中任务T1和T2导致FPGA区域碎片化，因此，即使FPGA上的总的空闲区域大于任务T3的区域，但任务T3也不能放置在FPGA上。

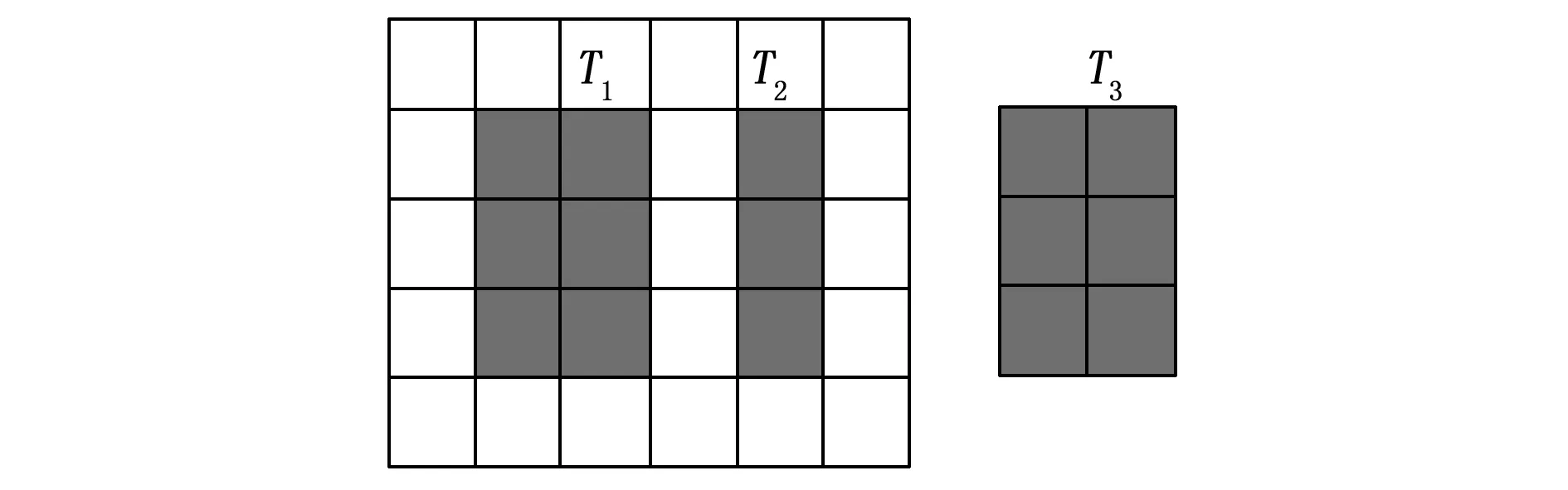
图1 FPGA区域的碎片化

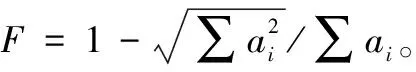
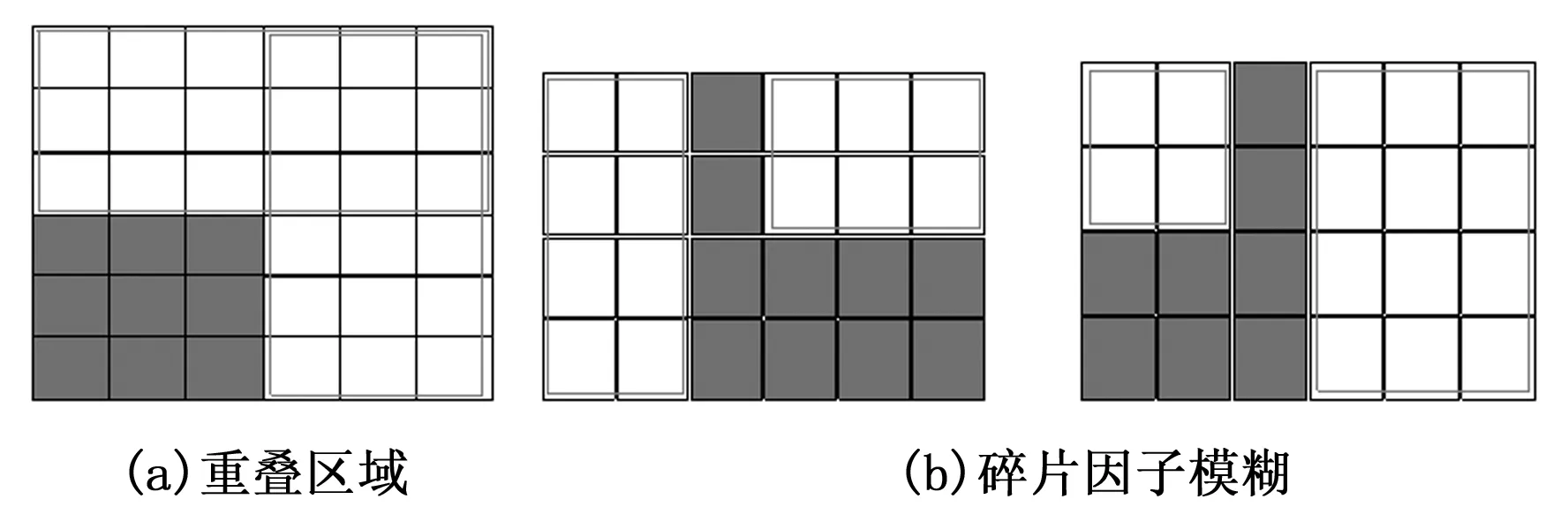
图2 碎片计算示例

上述这些方法都给出的是绝对的碎片度量，仅考虑了可重构单元的分布。

另一种发展趋势是相对碎片度量，它基于到达任务的大小考虑可重构单元的状态。作为相对碎片度量的一个例子，文献[15]根据任务的平均大小来进行计算。他们在一个空单元的垂直和水平附近使用空单元数量，如果这个数量大于或等于到达任务平均大小的2倍，则该单元的碎片贡献为0。总的碎片由可重构芯片区域内所有空单元的垂直碎片和水平碎片之和来计算；文献[16]基于多FPGA的动态可重配置的多任务调度和放置方法，通过任务级和子任务级的两阶段调度和放置方法，实现了在多FPGA系统的多任务调度和放置。在任务调度阶段，考虑任务相似性和资源需求相似性，为每个任务选择合适的计算单元，以减少重新配置和资源争用的可能性，在子任务调度阶段，综合考虑子任务的调度顺序和放置位置，以充分利用FPGA的硬件资源，利用FPGA可重配置能力使任务高度并行化，从而减小多任务的最小完工时间；文献[17]提出了一种HRCA系统的可重构单元的二维任务放置方法。方法结合3种影响HRCA系统的可重构单元的碎片产生因素，包括当前任务与其邻接任务在时间上的重合度，当前任务与其邻接任务的边长的重合度以及当前任务对其它空闲块的影响程度，依次计算当前任务的长、宽分别沿每个空闲块的每两条相邻边放置时的合适度，选出所有空闲块的所有位置中合适度最大的位置作为当前任务的最终放置位置。提出的可重构单元的二维任务放置方法，可以使任务放置更为紧凑合理，减少可重构单元中的碎片，提高可重构单元的空间利用率；文献[18]针对最佳匹配(BF，best fit)算法存在的缺陷，在目标处理器结点的局部调度下和避免最大入侵原则下，提出了一种避免入侵最佳匹配算法AIBFA。AIBFA算法分别降低了全局系统调度的平均时间负载率和目标处理器结点局部调度的任务拒绝率。针对寻找空闲资源全集的问题提出了一种基于单向栈的算法来寻找最大空闲矩形，利用可重构计算单元的不同M值进出单向栈来搜索到所有最大空闲矩形。实验表明，算法通过使用单向栈与算法优化，有效提高了查找空闲资源全集时的性能，减少了FPGA资源的碎片率；文献[19]针对目前可重构系统任务在线调度方法的不足，提出了一种基于放置代价的可重构系统软/硬件任务统一调度方法。方法考虑了3种代价，分别为硬件任务在FPGA上的执行时间、占用的FPGA面积以及FPGA的碎片情况，还考虑了软/硬件任务的统一调度方法。在调度过程中，当硬件任务的代价超过设定的阈值时，就拒绝其在FPGA上运行，并由CPU执行其相应软件任务实现.通过合理地拒绝一些代价较大的任务，从而从整体上提高任务调度成功率。实验表明，提出的方法能够获得更高的任务截止保证率。

相对碎片度量对特定时间到达任务的大小不敏感，所以对于相同的芯片碎片状态，可能在不同时间得到2种不同的碎片度量，而到达任务的大小也可能是高度变化的。因此，绝对度量更准确，它不需要给出芯片是满的或空的任何指示，相反，仅给出整个芯片区域的孔(或空区域)的分散程度。

对此，本文提出了一种测量区域碎片的新方法和利用这种碎片度量的在线任务放置。提出的碎片度量方法考虑的是可重构芯片上被占用(或空闲)空间的连续性，而不是被占用(或空闲)空间的数量。这样，可用于监测芯片区域和选择最佳的空区域来放置新任务，从而减少总的芯片区域碎片。基于一个二维结构的FPGA的仿真实验结果表明，相比于一般的左下角、第一匹配和最佳匹配放置策略，本文提出的碎片度量及放置方法不仅在等待时间、分配时间和响应时间方面有所改善，而且提高了芯片的利用率，降低了失配率。

1 系统模型

这部分给出本文所采用的部分可重构系统的任务和系统模型。

一个H×W的部分可重构FPGA芯片由H行和W列构成，左下角是芯片原点，在不影响芯片其余部分的情况下对芯片的一部分进行配置。由于单元按顺序配置，故FPGA是部分可重构的，重构时间与重新配置的单元数量成正比，配置延迟是配置一个单元及其相关路由资源所需要的时间。

系统假设任务在线到达，并按到达顺序排队和放置。只要在FPGA区域中有可用的空闲单元，服务器就会继续为到达的任务提供服务，方法是将每个任务放置在FPGA芯片的一个未被占用的区域上。如果由于没有可用的相邻资源(空闲单元)，队列顶部的任务被拒绝放置，则放置队列将处于停顿状态，直至存在足够的相邻空空间。

任务是非抢占的[20]。一旦任务被放置在可重构芯片区域的任何空闲区域，就停留在这个地方直至完成执行；任务参数事先是未知的，这些任务参数定义为：对于一个任务ti，ti=(hi，wi，ai，si，di，xi，yi)，hi和wi分别代表其高度和宽度，是用单元数量来度量的，ai、si和di分别为任务到达时间、任务服务时间和任务截止时间。分配给任务的矩形区域由其左下角(xi，yi)给出，其中xi表示行号，yi表示列号。这些特征能够反映一个通用计算系统。任务的大小、到达时间、服务时间和截止时间在一个预定义的区域都是均匀分布的，且事先未知的。

从形式上说，任务ti在时刻ai到达，在时刻si开始执行，在时刻fi完成执行，因此，任务ti的等待时间为w(ti)=si-ai给出，响应时间为r(ti)=fi-ai。任务的分配时间al(ti)是任务在等待队列的顶部等待直到它在可重构区域中找到一个位置的时间。

2 碎片度量

本节提出一种新的多维结构的碎片度量方法。假设单元是区域资源的最小单位，已使用的单元是指已占用的单元，未使用的单元称为空单元。我们从一维结构的度量开始，然后将它扩展到二维结构和更高维的结构。

2.1 一维碎片度量

首先给出一些定义。

考虑一个一维结构S，由L个单元构成，每个单元可以是占用的或空闲的两种状态之一，称这种结构为单元流。

定义1：长度为L的单元流S是一组L个连续单元。

备注：一个单元流表示一组连续的单元，而不考虑每个单元的状态。

定义2：长度为K的单元序列Q是一组K个连续的空单元。

在图3(a)中，存在长度分别为2、3的两个单元序列，而在图3(b)中，存在长度分别为1、4、5的3个单元序列。令c(S)为单元流S中单元序列的数量，QS(x)为单元流S中第x个单元序列，l(QS(x))为其长度(0≤x≤c(S))。

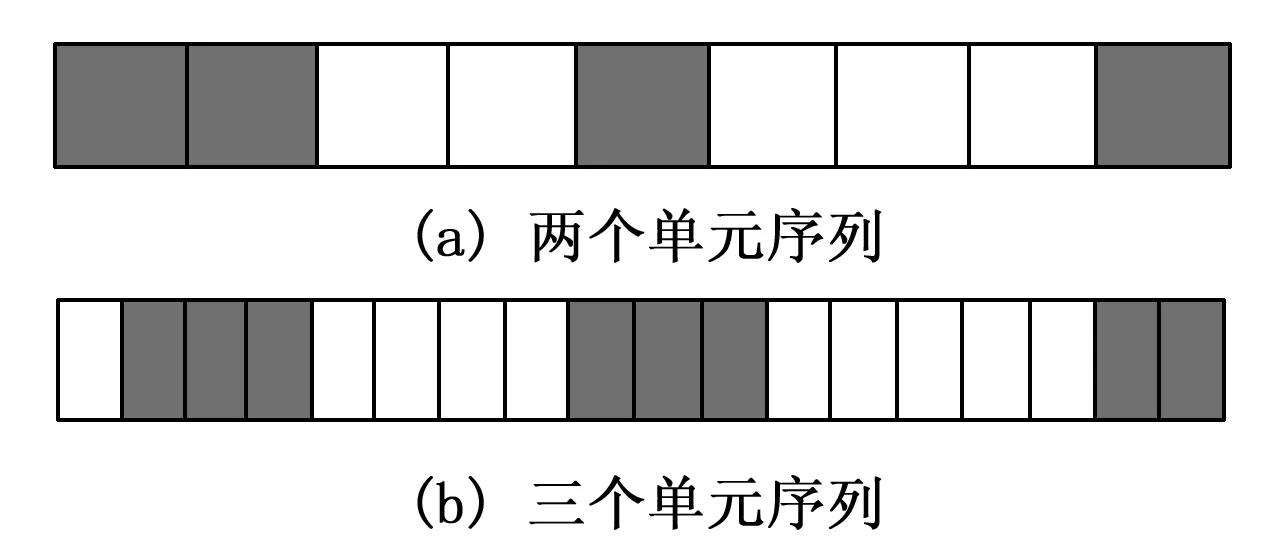
图3 一维碎片度量说明

引理1：在长度为L的单元流S中，单元序列数量c≤S[L/2]。

证明：当每个单元流的长度为1时，就会出现最大的单元流数量，即当单元序列中有一个空单元，然后是一个已占用的单元时，等等，就会发生这种情况。空单元的数量表示单元序列的数量，对于一个长度为L的单元流来说，它为L/2。

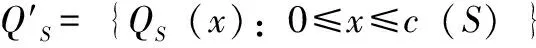
我们的度量指标测量在单元流内被占用区域的连续性，而不是测量有多少个单元是空的。因此，并不与具体的问题相关联，而是一个通用的度量指标，可以在不同的情况下使用。测量单元流中被占用单元的连续性，可转化为测量在单元流中有多少单元序列。具有小长度的许多单元序列的存在是高度碎片化的一个标志，我们建立在这一观察的基础上。

令FS表示单元流S的碎片度量，随着单元序列数量的增加，S的碎片也增加。每个单元序列的长度是计算S的碎片化的另一个重要因素，随着每个单元序列长度的减小，单元序列对碎片度量的贡献就更大。一个单元序列对FS贡献的值为1/l(QS(x))，则一维碎片度量为：

(1)

在图3(a)和(b)中，分别有F1-d=1/2+1/3=5/6，F1-d=1/1+1/4+1/5=29/20。

2.2 二维碎片度量

将上一节得到的一维碎片度量扩展到二维结构。考虑一个二维结构(阵列)A，由H×W个单元构成，每个单元可以是被占用的或空闲的两种状态之一。

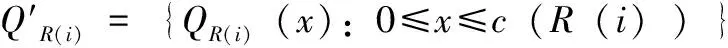
令FR(i)和FC(j)分别表示第i行和第j列对芯片的碎片度量F2-d的贡献，单元序列QR(i)对FR(i)贡献的值为1/l(QR(i)(x))，则：

(2)

在FPGA环境下，每行i对总的区域碎片度量贡献的值为FR(i)。令FR表示芯片中全部行的贡献值，则：

(3)

同样，每列对总碎片度量的贡献值为：

(4)

令FC表示芯片中全部列的贡献值，则：

(5)

最后，二维碎片度量F2-d可以计算为F2-d=FR+FC，即：

(6)

2.3 高维碎片度量

现在将前面的结果推广到n维结构，如超立方体。考虑一个n维单元阵列m1×m2×...×mn，令d1，d2，...，dn表示n维。这种结构中的基本单元是基本逻辑块(单元)。每个单元要么被占用，要么是空的。我们将考虑每个维度，并计算这个维度对碎片度量的贡献，将2.2节中的做法扩展到n维。可以通过确定单元所在的每个维度中的值来定义阵列中的单元。例如，单元C(x1，x2，...，xn)是位于d1维的x1，d2维的x2等等的一个单元，其中0≤xi≤mi-1，1≤i≤n。令Fd1，Fd2，...，Fdn分别表示d1，d2，...，dn维对碎片度量的贡献，令Qdr(x1，x2，...，xr-1，xr+1，...，xn)(k)表示维dr中第k个单元序列，1≤r≤n，且沿维d1，d2，...，dr-1，dr+1，...，dn的值分别为x1，x2，...，xr-1，xr+1，...，xn，令

{Qdr(x1，x2，...，xr-1，xr+1，...，xn)(k)：0≤k≤c(dr)}

(7)

为在维dr中单元序列的集合，同时令l(Qdr(x1，x2，...，xr-1，xr+1，...，xn)(k))为该单元序列的长度，把4.2节的结果进行扩展(这里1≤r≤n)，得到：

(8)

总的碎片度量是每维贡献的总和：

(9)

当n=3时，这个度量的一个直接应用是测量超立方体中的活跃节点有多分散。

2.4 碎片度量计算及实例

本节提出一种运行时间高效的算法来计算在给定时间的碎片度量。我们用一维阵列R(或C)的形式来保存行(或列)的碎片信息，碎片信息的更新是在每次添加和删除任务到FPGA之后。最初，当FPGA为空时，R和C中每个元素的值为零。

图4所示为有一些正在运行任务的一个芯片，代表芯片区域的阵列R和C在图中是沿列和行显示的，R(或C)的每个元素保存每行(或列)中相邻空单元的数量。元素R(i)(或C(j))包含行i(或列j)的碎片信息。R(或C)中的每个元素可能包含多个值，因为一行(或一列)可能有多个空单元序列。图4给出了一个6行6列的FPGA设备的示例。在图4中，R(0)=4表示第一行中相邻空单元的数量。C的第一个元素C(0)=[2，1]分别表示长度为2和1的两个不同的空序列。

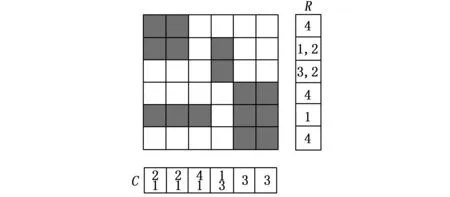
图4 计算碎片度量

芯片的碎片度量F2-d=FR+FC，其中，FR=1/4+1/1+1/2+1/3+1/2+1/4+1/1+1/4，FC=1/2+1/1+1/2+1/1+1/4+1/1+1/1+1/3+1/3+1/3。

3 基于碎片度量的任务在线放置

3.1 任务的添加和删除

在添加或删除任务之后，可以非常高效地更新碎片阵列R和C。当一个任务被添加或删除时，它只影响R和C的相应元素。如果将任务添加到芯片或从芯片中删除，已占用的行ri到rj和列ci到cj，则元素R(ri)到R(rj)将相应改变，以反映这些行的新的状态。对于元素C(ci)到C(cj)也是同样的分析。

3.2 任务的在线放置

根据其前面的讨论，碎片度量测量的是被占用(空闲)区域的连续性，也就是说，具有较低碎片度量值的芯片状态表示空闲空间的更多连续性，我们据此来选择到达任务的位置。

一旦一个任务位于队列的顶部，放置引擎就检查该任务的全部可能位置。放置引擎选择能够得到新状态较低碎片度量的位置，这将得到更多连续的空间，将有助于为下一组到达任务腾出空间。

碎片度量采用前述的阵列R和C快速计算，主要是找到最佳候选位置来放置任务，以减少新状态的碎片度量。可以根据任务大小、任务间到达时间和任务执行时间的不同分布，通过多次运行来观察这些参数对系统性能的影响。

4 实验结果

本节在二维结构上，通过对一个综合任务集的一系列实验来测试算法的性能。对于每个实验，生成1 000个任务的集合，任务由4个独立选择的均匀分布随机变量来描述，其中2个变量表示随机选择(均匀分布)的到达任务的长度和宽度，允许从1～32个单元不等；一个变量表示任务的服务时间，在1～1 000个时间单位之间随机生成(均匀分布)；任务的终止时间是通过在任务的服务时间中添加一个随机变量(在1～50之间均匀分布)来形成的。对均匀分布在1～(10，20，30，40，50，60，70，80，90，100)时间单位之间不同的任务间到达时间间隔重复实验；对这些任务进行排队，并按到达顺序放置到一个大小为64(64的仿真FPGA上。加载一个任务所需要的时间由芯片上空位置的可用性以及用于配置任务所需单元的时间确定，因此，每个单元的配置延迟也是一个参数，这里选择固定值1/1 000时间单位。

首先，在不采用实时截止时间测试的情况下，对于相同的数据集，将本文提出的碎片度量和放置方法与传统的放置策略左下角(BL，bottom-left)、第一匹配(FF，first first)和最佳匹配(BF，best fit)放置方法的性能进行比较，其次，在实时环境下对失配率进行测试。

图5和图6比较了传统的放置策略BL、FF和BF与本文提出的碎片度量及任务放置方法的不同性能。采用的一组输入数据任务侧可达32个单元，服务时间最大为500个时间单位，得到的不同任务间到达时间对各种性能的影响。

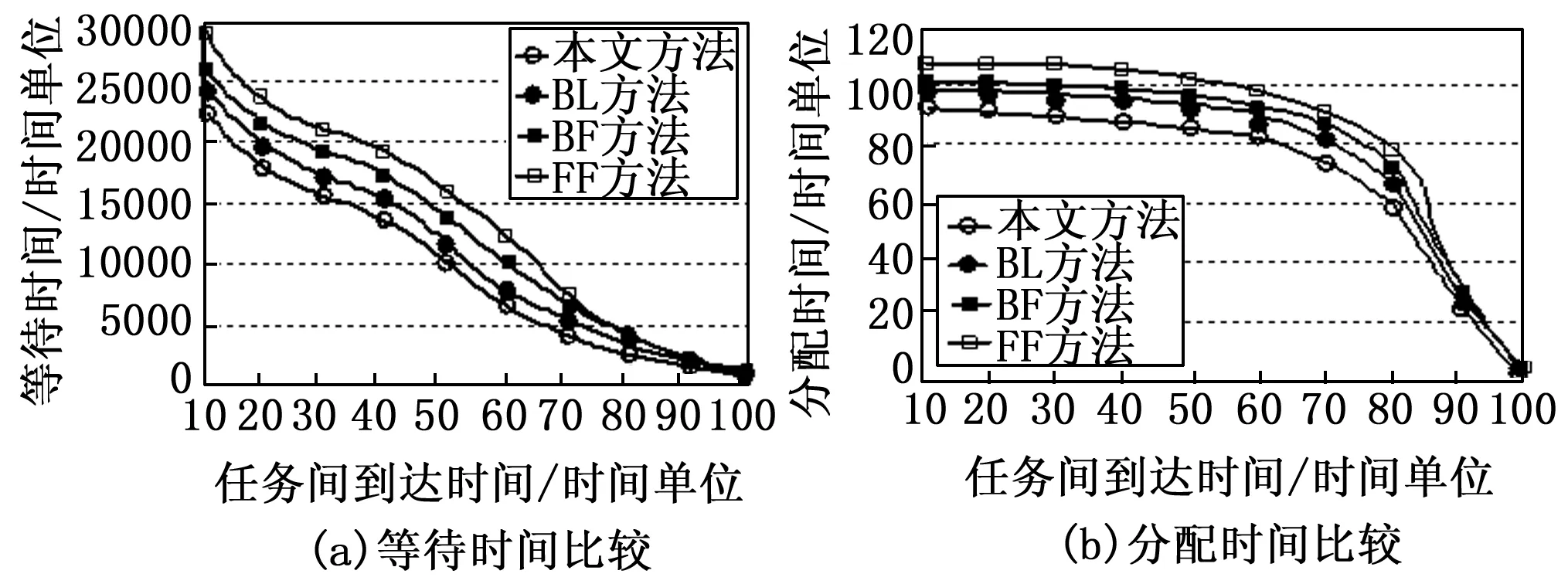
图5 性能测试1

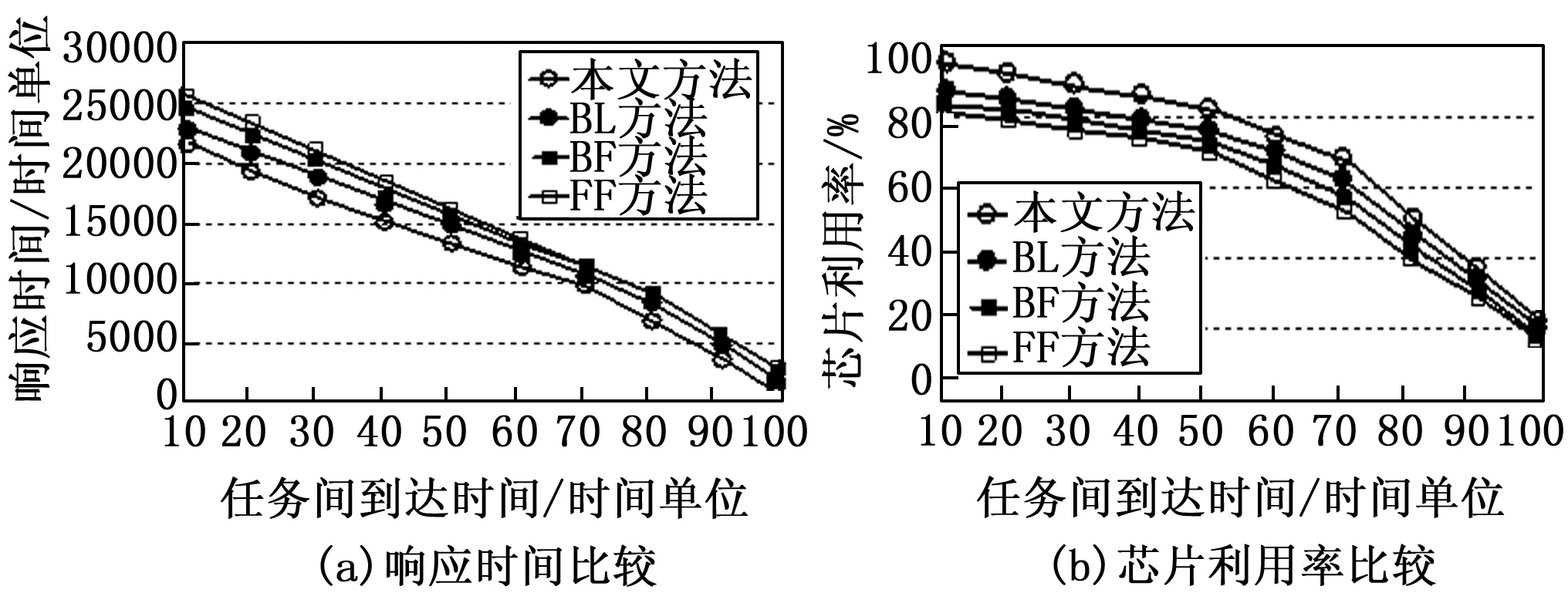
图6 性能测试2

图5(a)所示为不同放置放法的等待时间的比较。可见，本文提出的碎片度量及任务放置放法比BL平均降低了约10%，比FF平均降低了约25%，比BF平均降低了约13%；图5(b)所示为不同放置放法的分配时间的比较。可见，本文提出的碎片度量及任务放置方法比BL平均减少了约5%，比FF平均减少了约9%，比BF平均减少了约6%；对于响应时间，从图6(a)可以看到，本文提出的碎片度量及任务放置方法比BL平均降低了约10%，比FF平均降低了约16%，比BF平均降低了约12%；对于芯片利用率，从图6(b)可以看到，本文提出的碎片度量及任务放置方法比BL提高了约5%，比FF提高了约17%，比BF提高了约13%。

表1所示在实时环境下，本文提出的碎片度量及任务放置方法与BL、FF和BF相比在失配率方面的改进。第一列的任务大小从1×1到32×32、第二列从8×8到32×32，等等。从表1可见，在第一列的任务大小中，任务间到达时间为90个时间单位时有最佳的改进。随着最小任务边长的增加，失配率有更大的改进，这是因为小任务可以放在芯片中的一些碎片中；当最小任务侧为24个单元时，本文提出的碎片度量及任务放置方法的失配率改进效果较好。

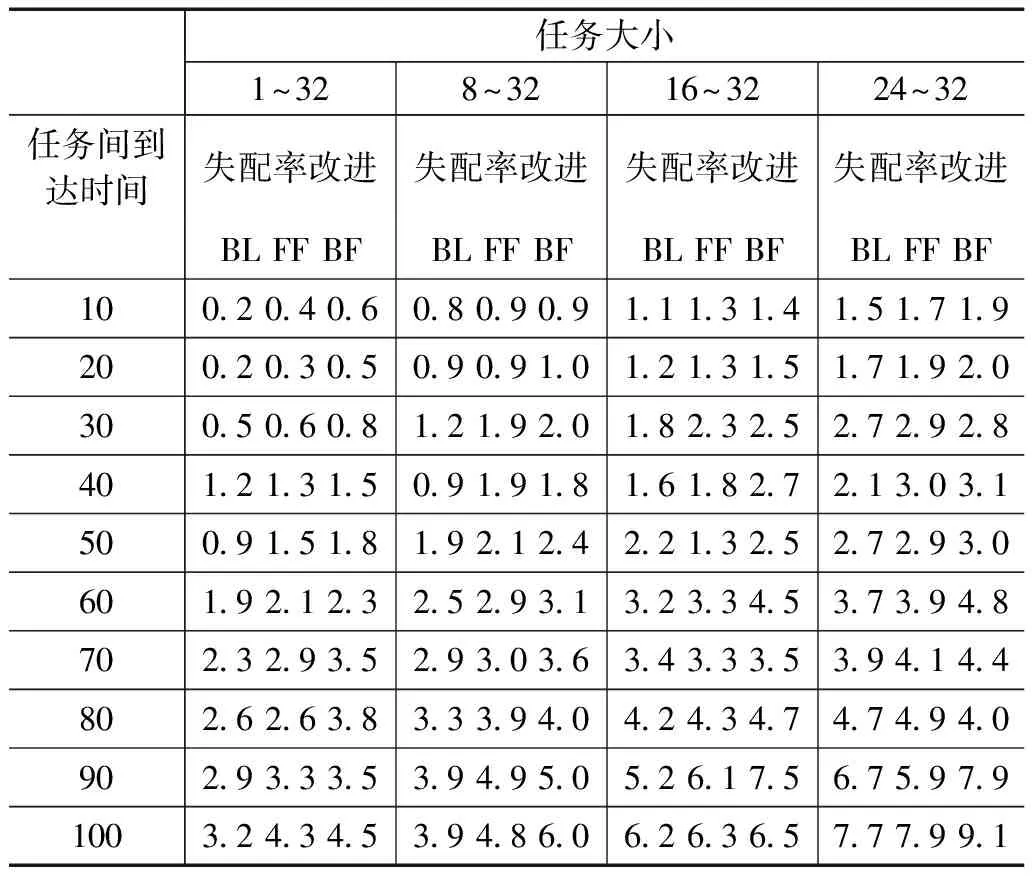
表1 本文方法相比于BL、FF和BF的失配率改进 %

5 结束语

本文针对部分可重构FPGA提出了一种多维碎片度量及任务的在线放置，并在二维结构中采用这个度量来提高FPGA的区域利用率。实验结果表明，本文提出的碎片度量及任务在线放置方法与常用的放置策略如左下角、第一匹配和最佳匹配相比较，在芯片利用率方面提高了约5%～17%，在响应时间方面降低了约10%～16%；在实时系统中的测试表明，失配率最大可改进约9%。

将本文提出的放置方法应用于异构可重构系统将是我们未来一段时间的研究方向。