基于不同内膛结构参数的弹带挤进阻力特性研究*

刘 琦 王育维 朱文芳 郭映华

（西北机电工程研究所 咸阳 712099）

1 引言

身管在火药燃气作用下内表面发生周期性的冷热循环作用，导致内膛表面发生磨损，尤其身管膛线起始部最为严重，当这种磨损作用达到一定程度，身管就会失去应有的弹道性能［1］。造成这种磨损的原因是复杂的，其中弹丸的摩擦作用、弹丸的挤压作用及弹带定心部与身管膛线的高速摩擦作用为主要方面。身管磨损导致弹丸出炮口不再满足旋转稳定与初速或然误差的要求，从而导致火炮技战术水平难以发挥［2］。

图1 为某大口径火炮最大膛压及初速随内膛磨损量的变化规律曲线，最大膛压及炮口初速均随身管的磨损量增大有不同程度的降低。可见，内膛烧蚀磨损量对最大膛压及初速有着重要影响，因此，深入研究身管磨损规律及其所造成的膛线结构变化，对身管武器一体化设计、身管结构优化、弹带材料的选择、内弹道初速稳定性分析、内弹道与装药结构设计与优化等具有巨大的理论意义与工程实用价值。

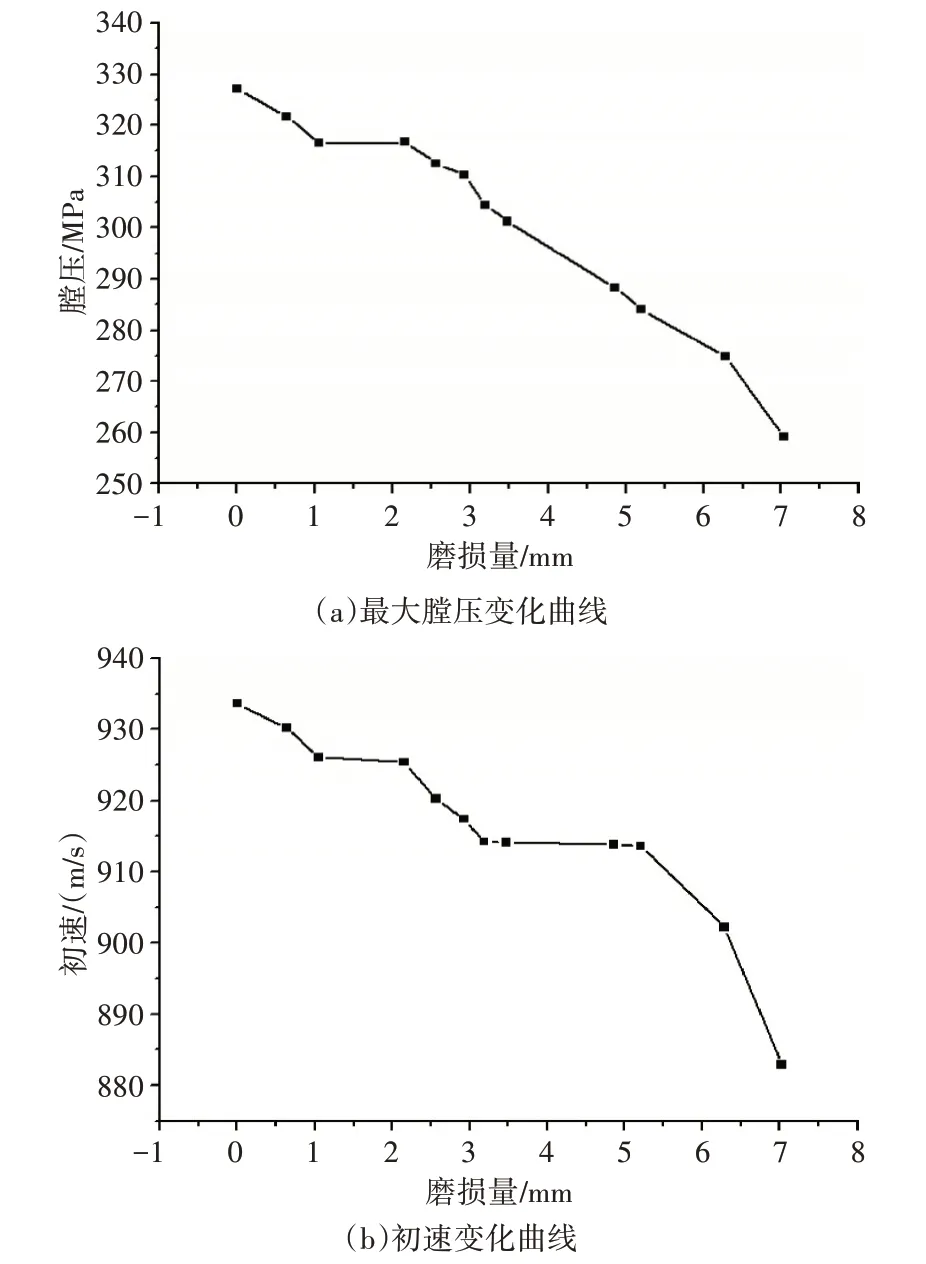
图1 某大口径火炮最大膛压及初速随内膛磨损量的变化曲线

本文在前期研究工作基础上，以某大口径榴弹炮为研究对象，考虑高速高压环境中的滑动摩擦力变化，同时考虑挤进过程中的能量守恒准则，将经典内弹道方程组与弹带挤进过程耦合起来，进行直接耦合求解。同时运用显式动力学算法对比不同膛线结构参数下弹带挤进过程的差异。分析不同膛线结构参数对弹带挤进过程受力状态的影响，得到挤进系统主要结构参数对弹带挤进过程的影响规律，从而为身管武器一体化设计、身管结构优化、弹带材料的选择、内弹道初速稳定性分析等提供参考。

2 理论基础

2.1 内弹道方程组

挤进时期经典内弹道方程如下［3～4］：

将上述公式合并后，得到以下微分方程：

式中：lψ=l0[1-Δ(1-ψq)/ρq-αqΔψq]；l0为药室容积缩径长；fq为火药力；ρq为火药的密度；αq为余容，As为炮膛橫截面积；u1为燃速系数；sn为压力指数，e1为火药弧厚，χ、λ、μ均为火药形状特征量，θ为内弹道参量。采用四阶龙格库塔方法求解式（2），初始值设为弹丸启动压力。

2.2 膛内运动时期弹丸受力分析

弹丸膛内运动时期，若弹丸质量为m，则弹丸的转动惯量为I=mρ2，ρ为惯性半径，弹丸的转动角速度为Ω，参照牛顿第二定律，则［5～6］：

其中，后坐质量为M，发射药质量为w，则有：

其中，νw为未燃尽药粒及燃气的平均速度，可取，由于：

则弹丸运动方程为

2.3 Johnson-Cook本构模型

弹带挤进过程的受力和变形情况非常复杂，不仅产生塑性变形，还受到火药气体高温以及高应变率的作用，在本文所建立的有限元模型中，弹带材料采用的本构模型为Johnson-Cook 模型，Johnson-Cook材料模型由两部分组成。

第一部分：Johnson-Cook塑性模型

在此模型中，Von Mises 屈服应力是塑性应变、应变率以及温度的函数［7］。式中，εp为等效塑性应变；为等效塑性应变率；为参考应变率；T为温度；Tr为参考温度，一般取室温；Tm为熔化温度；A、B、C、m和n是常量。绝热形变所造成的温度改变为［8］

式中，ρ为材料密度；cp为定容比热；χ为Taylor-Quinney系数。

第二部分：Johnson-Cook断裂失效模型

Johnson-Cook 断裂模型通过等效塑性失效应变界定损伤［9～10］：

D1～D5为材料断裂失效参数；σ*为应力三轴度［11］：

3 弹带挤进过程耦合模型

3.1 几何模型

弹带挤进过程几何模型如图2 所示，弹丸从卡膛初始位置起，受到膛内火药气体的推动作用，克服弹带变形阻力沿坡膛轴向推进，直到弹带刻槽完成，弹丸全部进入全膛线深。

图2 弹带挤进过程示意图

3.2 有限元模型

应用动力学分析软件建立有限元模型，应用HYPERMSEH 软件对弹带刻槽部分采用无网格光滑粒子流体动力（SPH）算法进行处理，划分的身管与弹体有限元模型分别如图3、图4。有限元模型中弹带刻槽SPH粒子与弹带不刻槽部分采用点-面绑定接触，SPH 粒子与身管内壁的接触定义为自动点对面接触，弹带不刻槽部分与弹体之间、弹体前后定心部与身管内壁之间的接触定义为自动面对面接触［12］。采用罚函数法进行计算以及检测点-面及面-面接触［12］，相当于在主从节点的接触面之间设置一个法向弹簧，以限制从节点对主表面的穿透，最终划分的弹带有限元模型如图5。

图3 身管有限元模型

图4 弹体有限元模型

图5 弹带有限元模型

3.3 材料参数

本文的模型中弹体材料为合金钢，身管材料为炮钢，在本次模拟中均采用弹塑性本构模型，材料参数如表1所示。

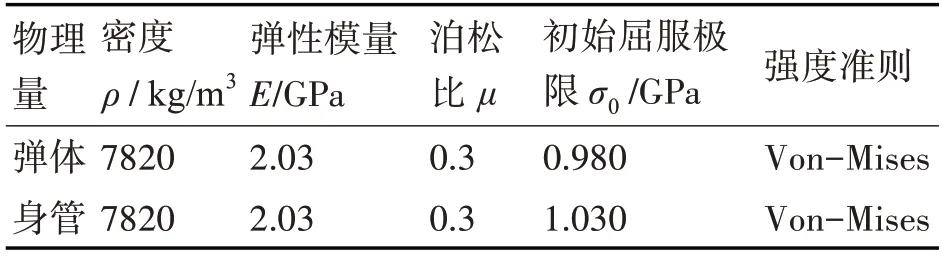
表1 弹体及身管材料参数

由于高应变率变形通常伴随应变硬化、应变率硬化及温度软化，因此本构模型中通常将应力与应变、应变率和温度联系起来，通常表示为［7］

其中，σ是应力，ε是应变，˙是应变率，T是温度。Johnson 和Cook 提出了一个考虑应变、应变率和温度对应力影响的经验模型［12］：

其中，A，B，n，C，m是材料常数；σy为等效应力，，sij为偏应力张量；为等效塑性应变，，εij为应变张量；为无量纲化的应变速率，˙为应变率；为参考应变率；T*=(T-Tr)/(Tm-Tr)为无量纲化的温度，Tr为室温，Tm为材料的熔点，通过试验数据可以回归出材料常数A，B，n，C，m［12］。所谓的回归分析法，就是寻找最优的参数A，B，n，C，m，使得：

本文在冲击试验的基础上，经非线性拟合得到：A=133 MPa，B=324 MPa，n=0.48，m=1.21，C=0.043，将该材料属性输入到有限元模型中用于弹带挤进过程的计算。

3.4 计算工况

为了简化模型，忽略次要影响因素，对弹带挤进过程作如下简化：不考虑卡膛过程，即弹丸初始位置为弹带与坡膛起始段接触位置，忽略弹带的初始应力与变形；卡膛到位后，认为弹带和坡膛倾角紧密配合，并将此位置作为弹丸挤进过程的开始；忽略不均衡问题，假定弹丸与身管轴线共心，摩擦力与运动阻力都沿轴线方向；忽略弹丸前部的空气阻力和激波的影响；不考虑身管与弹丸在重力下产生的应力与变形；不考虑身管的后坐运动。目前，对身管损伤，尚缺乏有效描述方法。身管在使用过程中，烧蚀磨损导致的典型损伤有两种：坡膛损伤和线膛损伤，以特征量值来表征，具体包括坡膛长度变长和膛线形状变化（阳线高度减小和阳线宽度变窄）等情况，本文分别对这两种典型损伤的三种情况下的弹丸挤进过程进行数值模拟和分析研究。本文所计算的某大口径榴弹炮坡膛长度为101mm，而模拟磨损坡膛取坡膛长度为120mm；正常膛线阳线高度为1.27mm，而模拟磨损膛线高度为1.1mm，正常阳线宽度为3.81mm，而模拟磨损膛线宽度为3.5mm。

4 结果分析

4.1 数值计算结果

本文计算了坡膛长度为101mm、阳线高度为1.27mm 及阳线宽度为3.81mm 时某大口径榴弹炮的弹带挤进过程，计算结果如图6～图10，其中图6为挤进完成时弹带温度场分布，可以看出，弹带最高温度为189℃，远低于弹带材料的熔融温度1086℃。图7 为挤进完成时弹带应力场分布，最大应力为569MPa，超过了弹带材料的静态屈服应力123MPa，材料发生屈服变形。图8为挤进完成时弹带的塑性应变分布，刻槽完成时，弹带的最大塑性应变率为1.528，且后弹带的应变率大于前弹带。图9 和图10 分别为耦合计算的弹丸膛内速度与加速度曲线，图11 为挤进过程挤进阻力变化曲线，从图11 可以看出，在两条弹带刻槽时刻之间，弹带挤进阻力有一段波谷；弹带动态挤进阻力变化规律与经典理论中准静态模型的挤进阻力曲线有较大差别，最大挤进阻力为88.9KN，而准静态值为86.68KN，动态挤进阻力值略高于准静态挤进阻力。

图6 挤进完成时弹带温度场分布

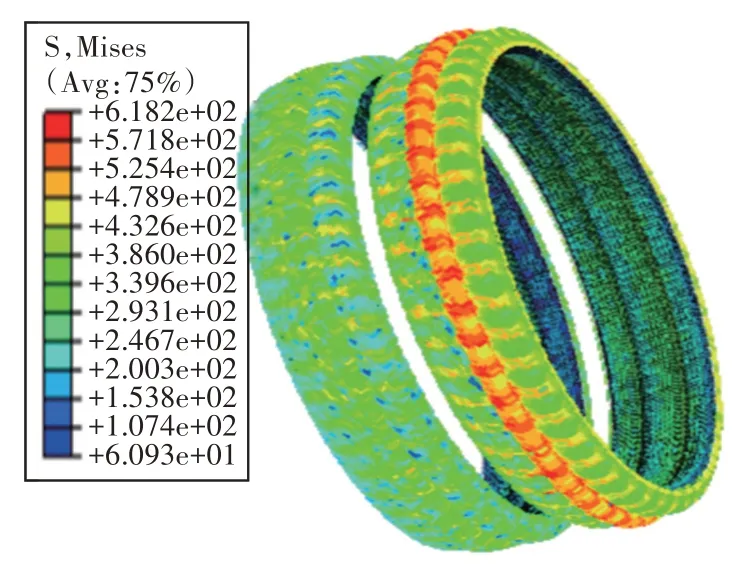
图7 挤进完成时弹带应力场分布

图8 挤进完成时弹带塑性应变场分布

图9 弹丸速度曲线

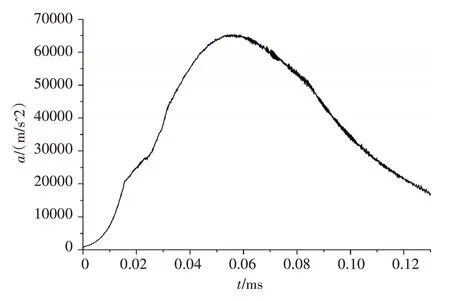
图10 弹丸加速度曲线

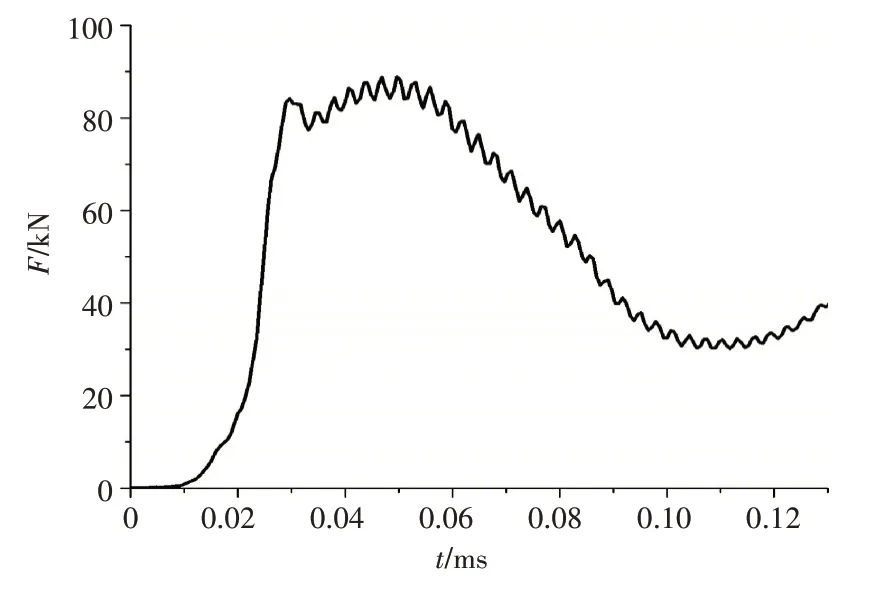
图11 挤进阻力变化曲线

4.2 坡膛磨损对挤进阻力的影响

用坡膛长度的减小模拟身管在使用过程中的坡膛磨损，弹带、弹丸及膛线高度的尺寸均保持不变。图12 为坡膛长度分别为101mm 和120mm 时弹带沿程挤进阻力的变化，从图中可以看出，坡膛长度变长，弹丸运动阻力减小，挤进压力变小。

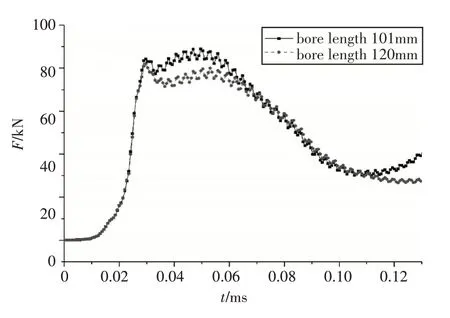
图12 不同坡膛长度挤进阻力对比

用身管膛线阳线高度的减小模拟身管在使用过程中的膛线磨损，图13 为阳线高度分别为1.27mm 和1.1mm 时弹带沿程挤进阻力的变化，从图中可以看出，线膛损伤后，阳线高度降低，这种情况下相当于挤进时弹带过盈量和强制量相对减小，弹丸与身管之间的作用趋缓，可以理解为坡膛相应位置最大应力较小，弹丸挤进相对容易，弹带挤进阻力的最大值由88.9KN降低为79.3KN。

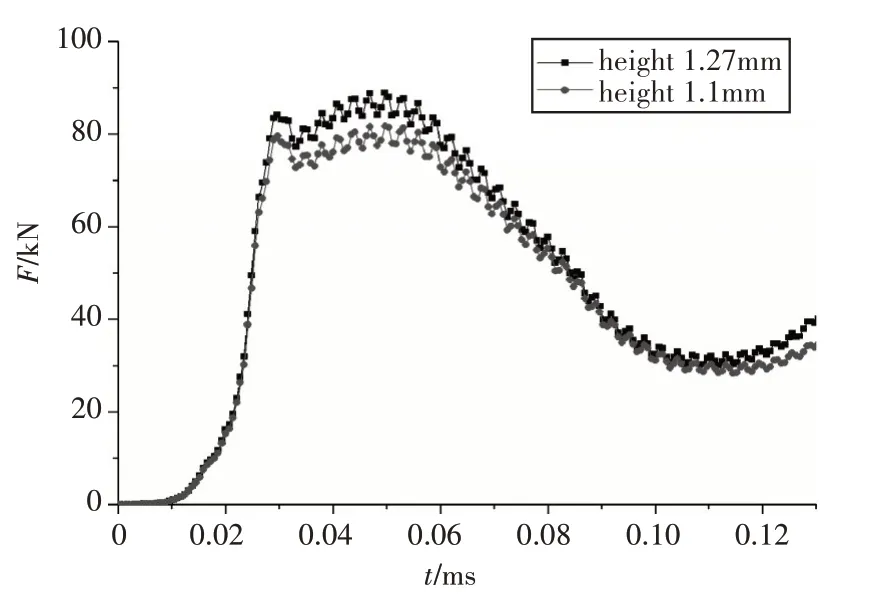
图13 不同阳线高度挤进阻力对比

用阳线宽度的减小模拟身管在使用过程中膛线导转侧的磨损，图14 为阳线宽度分别为3.81mm和3.5mm 时挤进阻力的对比，从图可以看出，阳线宽度变小，弹丸挤进过程中的初始阻力减小。阴线宽度的相对增加，给弹带提供了更大的材料流动空间，弹带挤进更加容易，最大挤进阻力降低为77.8KN。

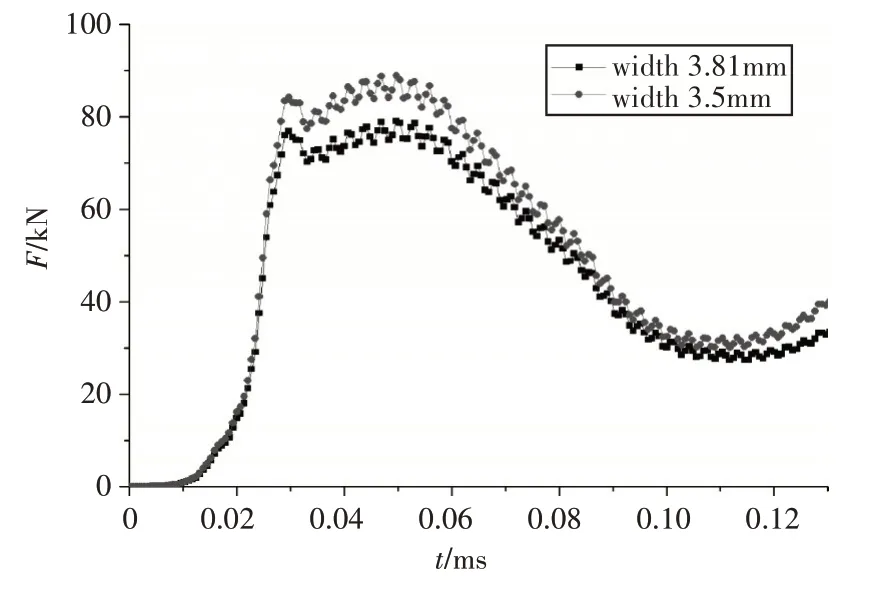
图14 不同阳线宽度挤进阻力对比

5 结语

本文将经典内弹道方程组与弹带挤进过程进行耦合，建立弹带挤进过程耦合动力学模型，对某大口径榴弹炮弹带挤进过程进行了计算，在此基础上，对比了不同坡膛结构对弹带挤进过程挤进阻力的差异，得出以下结论：

1）弹带动态挤进阻力变化规律与经典理论中准静态模型的挤进阻力曲线有较大差别，最大挤进阻力88.9KN，而准静态时此值为86.68KN，动态挤进阻力值略高于准静态挤进阻力。

2）弹带挤进完成时刻对应膛底压力为168MPa，比经典内弹道理论中挤进压力取经验值30MPa 要大得多，因此，传统的挤进压力假设误差较大。

3）挤进过程中弹带绝热变形产生的热量不足以使弹带材料熔化，最高温度为189℃，未达到材料熔化温度，因此弹带在挤进过程中未发生熔融。

4）坡膛长度变长，弹丸运动阻力减小，挤进压力变小；膛线阳线高度减小，挤进时弹带过盈量和强制量相对减小，弹丸与身管之间的作用趋缓，弹丸挤进相对容易，弹带挤进阻力降低；阳线宽度变小，弹丸挤进过程中的初始阻力减小，阴线宽度的相对增加，给弹带提供了更大的材料流动空间，弹带挤进更加容易，最大挤进阻力降低。