复杂水域中的无人艇群分散式控制*
刘 洋 王 征 尹 洋 龚谢平
(海军工程大学电气工程学院 武汉 430032)
1 引言
无人艇技术经过几十年的发展已经相对成熟,在军事和民事领域发挥了重要的作用。为了适应未来复杂的水面任务,除了提高无人艇的机动性能,还需要考虑如何以现有的技术基础,发展更加有效的无人艇管理和组织模式。考虑到单艘无人艇的功能对任务需求面覆盖窄的缺点,近些年的研究热点正在逐步由单艇向多无人艇编队协同靠拢,如:蜂拥、集群、聚集、涡旋覆盖、编队任务等。
目前协同研究大多集中在无人艇的编队、队形控制方面,其控制结构的设计方法主要有领航跟随法[1]、虚拟结构法[2]、行为分解法[3]等,试验证明这些控制结构可以较好地在空旷无干扰水域中完成队形控制运动。按照体系结构可将多无人艇系统分为集中式、分布式和分散式[4],其中部分研究为集中式或者分布式控制结构,其明显特征为结构中存在一艘或多艘领航无人艇,这样的结构可以比较快地找出全局最优路径,有较高的多边协商效率,但也可能会有如在通过狭窄航道时灵活性较差、单个无人艇意外损耗影响整个集群效率的问题,且随着无人艇的数目增加,无人艇间的相互协调工作的难度也会随着群体的复杂性、动态性及耦合性指数倍增长。
而分散式控制结构有较好的稳定性以及故障冗余的特点。因此,本文试图采用分散式结构,在Boid群集模型的基础下设计无人艇集群控制结构,通过短程斥力避免个体碰撞,利用隐含的类粘性摩擦对齐规则项来抑制系统缺陷导致的振荡,同时通过引入软控制的概念建立虚构的“shill”无人艇对全局的无人艇进行约束以及避障,以提高无人艇集群的扩展能力以及降低群体复杂性。
2 无人艇建模
无人艇作为一个具有横摇、纵摇、艏摇、横荡、纵荡、垂荡六个自由度的刚体模型,控制耦合会非常的复杂。而无人艇的控制主要在于方位,因此本文在纵荡、横荡以及艏摇三个自由度上建立欠驱动的以螺旋桨为推力的无人艇的数学模型[5]。其运动学模型可以表示为
式中,η=(ηx,ηy,ψ)中ηx和ηy表示船体在北东坐标系下的位置,ψ表示艏向角;ν=(w,ν,r)中w和ν分别表示船体在船体坐标系下的前向速度和横向速度,r表示艏向角速度。
其动力学公式表述为
式中,M为惯性矩阵;C(ν)为科氏力和向心力矩阵;D(ν)为水动力阻尼矩阵;τ=[τu0τr],是无人艇所受的推进力和转向力矩;τe=[τeu τeν τer]为外界环境干扰。
以固定距螺旋桨为动力的无人艇的推力和转向力矩由螺旋桨转速δn和推力偏转角δs决定,Fossen指出一般情况下,推力T是船速V和螺旋桨转速δn的函数[6]:
式中,c,d是与海水密度、螺旋桨螺距相关的常量。因此τu,τr分别为
式中,xcenter为螺旋桨到船质心的距离,为动力臂。因此在T+1 时刻,可以通过计算得到期望速度vdesire,同时T 时刻的速度V和vdesire作为输入通过PD控制可以得到T+1时刻的期望螺旋桨转速δn和推力偏转角δs,式(2)、(3)联立从而实现无人艇的动力学控制。
3 无人艇集群运动分散式控制策略
如图1 所示,分散式控制中的每艘无人艇可以相互观察、交换信息,但它们不发送和接受直接控制命令,原因是分散式控制旨在避免群体中存在主从关系,这点是与集中式和分布式结构不同的地方。本文设置无人艇不存在主从关系,即每艘无人艇都遵从同样的运动控制准则,控制律由整体结构所控制。
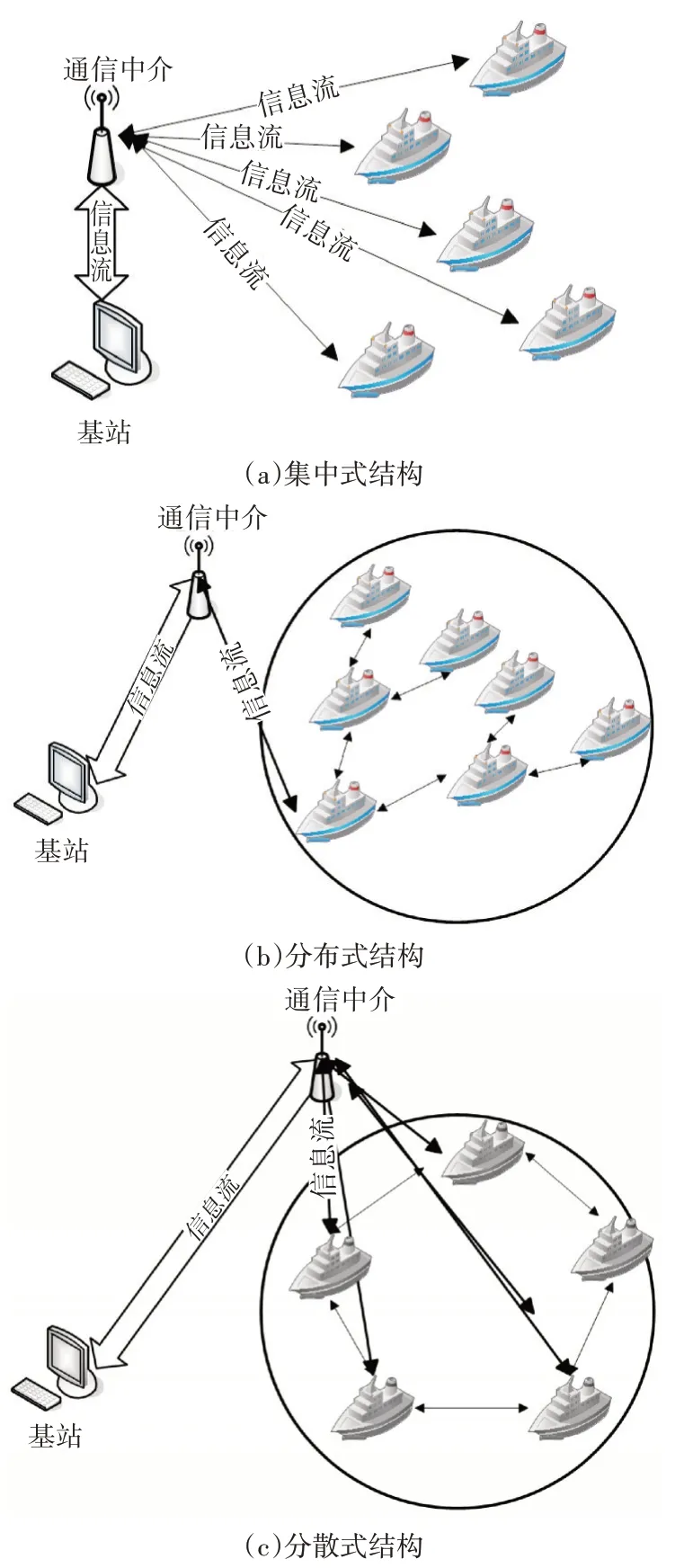
图1 集中式结构、分布式结构和分散式结构
自然中有很多生物聚集行为,例如飞翔鸟群,它们没有统一的控制平台,也没有固定的领航者,每只鸟都是一个独立的个体,通过对动态环境的局部感知完成复杂优美的集群运动。类似这样的集群,Gábor Vásárhelyi 等[8]将其称之为自组织系统(the Self-organized System)。自组织系统中对象采取的行为模式由系统中的其它单元的集体效应决定,相邻个体的物理量倾向于彼此对齐,这种行为和潜在的控制机制应该是安全、稳定和无碰撞运动的先决条件[8]。
基于Boid蜂拥运动模型,这种控制结构可描述为以下三条基本准则:
1)避免碰撞:短距离内要保证无人艇个体不发生碰撞;
2)速度匹配:通过局部交互使无人艇个体与局部小群落速度对齐;
3)全局约束:保证无人艇集群在一个约束范围内。
3.1 短程排斥项
为了避免无人艇之间的碰撞,且防止传感器位置测量误差高阶项而导致斥力的突变或产生奇点,本文设置一种类似于势场力的短程分段斥力:
式中,R是斥力常数,rij是无人艇i和无人艇j的距离矢量;r0是短程斥力的影响范围,也就是说,超过这个距离的无人艇之间不存在短程斥力;γ即为短程斥力的宽度,避免无人艇之间激发过度互斥。
3.2 局部速度调整项
在无人艇的集群中,无人艇的通信范围通常是有限的,只能向通信半径内的其它艇发送信息,最简单的基于agent的集群模型将对齐规则描述为明确的数学公理:即每个单元将其速度向量对齐到临近单元(包括自身)的平均速度向量。Yoram Koren[9]势场法是一种简单明了的避障方法,但其自身明显的缺点是当无人艇及障碍物分布过多时会造成不稳定的振荡运动。因而提出对齐规则应是基于过阻尼动力学的相互作用力或速度项的结果,以避免短程斥力可能会出现的不稳定振荡,同时促进局部镇定[10]。
因此设置一个类摩擦粘滞力,使一艘无人艇跟随周围影响半径内无人艇达到同步,同时该项作为减震媒介,减少由于排斥等延迟和嘈杂的环境而出现的自激振荡,并且可扩展到比较高的速度的情况。
式中,表示无人艇i和j在欧氏距离‖rij‖下的可允许最大速度差值,一旦无人艇i和j和的速度差‖vij‖大于该值,局部调整就要作用于无人艇i从而使其状态向j靠拢;是最大速度差的临界点,如果两者之间的距离小于该值,则该范围内的任何两艇的最大速度差都维持在一个较低的速度值νfrict上,使在一定近距离范围内的无人艇都会受到较大的局部速度调整影响;K是耦合系数,K>0;d则是调整函数f(rij,,d)的衰减速度,以用来适应不同速度的集群行为;N是在局部速度调整范围R下与无人艇i邻接的其它艇的个数;νij是无人艇i和j的速度矢量差。
f(rij,,d) 基于Cucker-Smale 的N-体运动模型[10]提出,薛小平[12]证明参数β<1/2 时,任何状态下的个体均可达到渐近群体效应,即:
1)相对速度趋于0,即
2)相对位移聚集,即
图2 是可视化作用力,其中红线表示了无人艇之间的排斥力与距离之间的分段函数关系;绿线是无人艇i和j在某距离下的最大速度差,如果两艇的速度差位于绿线之上(如图中红点‖νij‖),则局部调整速度项会作用于无人艇i,直至‖νij‖位于绿色区域。此函数可以通过改变允许无人艇在某距离下之间的最大速度差来调整适应不同的无人艇群的数量和集群速度等,具有较好的扩展性。
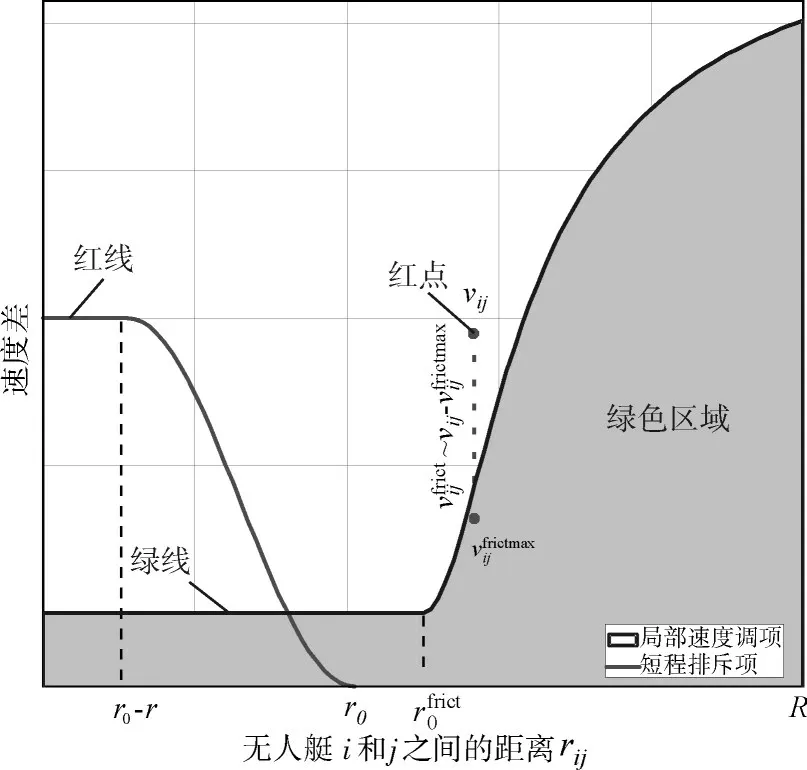
图2 可视化作用力
3.3 全局位置约束项
韩晶[13]提出了“soft control”、“shill”的概念,其思想即:集群行为是多智能体系统的一种宏观特征,在一个多智能体系统中,多数智能体是具有局部规则的普通智能体,当在群体中加入一些受控制的“shill”诱导无人艇单元后可以使集群行为随着受控“shill”改变,实现所谓的软控制(软控制和分布式控制的区别在于:分布式控制中每个智能体是一个控制系统且有它自身的控制律;而软控制中将所有的智能体看作一个系统,控制律是作用于“shill”而非直接作用于单个智能体)。
因此本文设置一个虚拟的“fence”的概念,将构成凸多边形的边上的每个点视作一艘shill 无人艇,对整个无人艇集群行为进行软控制。为了使无人艇群能够像生物群体一样完成集群运动,每一个shill 无人艇,它们均有一个指向fence 内部的速度,从而诱导无人艇集群收缩至设定的范围内;同样栅栏内的障碍物也可以将其视作shill无人艇,它的诱导方向是由障碍物向外发散,由于分散控制中每个智能体遵循的控制律都一样,所以任意无人艇i和虚拟shill无人艇也遵循局部速度调整公式:式中,shill 是指距无人艇i最近的任意凸多边形fence 的点所形成的虚拟无人艇;是指无人艇i与shill无人艇之间的最大允许速度差异;ris是指无人艇i和shill 的欧氏距离;x是无人艇i与fence 的相对中心点的欧氏距离,Rs是该shill 无人艇与fence 的相对中心点的欧氏距离,b是缓冲宽度。当无人艇在该距离之外时,通过shill无人艇的诱导使其逐渐向fence 靠拢,通过调节缓冲宽度b可以适应不同的聚集程度和集群速度;Robstacle是允许的无人艇与障碍物之间的极限距离,小于这个距离将会通过局部调整避开障碍物。
3.4 集群速度项
为使无人艇群完成集群运动,将fence 视作一个刚体运动,通过作用于刚体中心的控制律来控制无人群进行定向、定点或者是跟随等等任务。在定向集群运动的情况下,本文为无人艇设置一个自驱动速度项[14],保持无人艇拥有值为Vflock的恒定群集速度。
而在定向集群运动中,我们则需要设置一个朝向目标点的集群速度,因此自驱动速度为
式中,xtarget为目标点矢量;xfence为栅栏中心矢量。
3.5 最终期望速度
最后本文将上述作用项取矢量和,即可得到下一时刻无人艇i的期望速度:
4 多无人艇集群运动性能评价指标
多无人艇做集群运动应该满足这样的特点:集群的个体应该朝着目标方向排列,作为一个紧密的、连贯的类似链接起来的群体以平稳、快速的方式做不发生碰撞的移动。在集群运动模型中,集群过程是一个从无序到有序的类似相变的转变过程,本文通过借用相变理论中对物理系统的有序化程度的刻画从设定一个或者多个所谓的序参量(order parameters)的特定系统变量来描述集群的程度[15]。序参量指的是表征一个相的对称度,这个值通常在一个相(无序相)为零,在另一个相(有序相)中为非零。因此本文选择平均归一化速度和聚集态相干性两个不同方面的序参量作为评估无人艇集群运动的指标。
4.1 平均归一化速度
在集群运动的情况下,最优先选择的序参量是平均归一化速度ψνel:
其中N 是无人艇总数,ν0是无人艇集群的平均绝对速度。如果无人艇群运动是无序的,单个无人艇的速度是在随机方向指向一个小的数量级矢量;而对于有序运动,所有无人艇速度的矢量和的绝对值接近于Nν0,因此序参量ψνel可以是表示一个从0~1 的连续相变的过程。它表示了一个集群的速度指向的一致性,当该参量接近1 时表明集群正在向同一方向运动,当该参量接近0 时表明该时刻集群正在做无序运动。
4.2 聚集态相干性
群体聚集态的相干性可以衡量整个无人艇群的聚集离散程度:
该序参量捕捉了无人艇行动的速度相关性,并给出无人艇群有序程度。
5 实验结果及分析
本文在实验假设的多礁水域进行多无人艇集群运动数值仿真以验证所提出的分散式控制策略的有效性和准确性。其仿真流程图如图3 所示,本文选用的无人艇模型主要物理参数如表1所示。

表1 无人艇模型物理参数
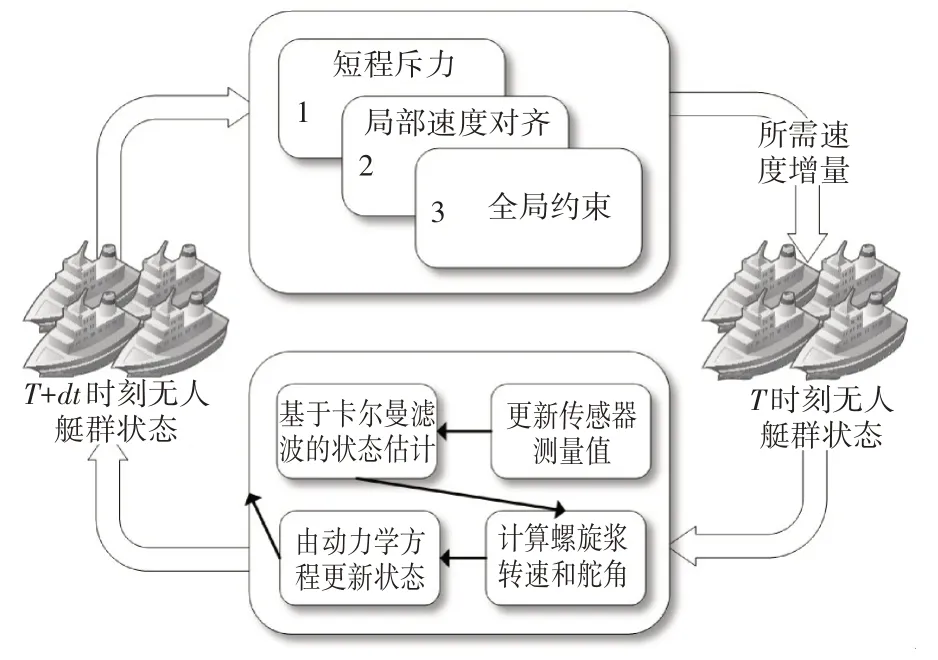
图3 分散式控制示意图
仿真实验中本文设定局部通信约束的最大范围为150m,最大邻接无人艇数量10 艘,无人艇碰撞半径1.5m,定义fence为边长为50m 的正方形,无人艇初始位置、姿态均围绕fence的中心随机分布,初速度均为0。
实验一选择7 艘无人艇完成正北向的定向无人艇集群运动实验,设置栅栏的初始位置为[170,-25]m,仿真结果如图4。从仿真中可以看出t=0s 时无人艇随机分布于fence 四周,随后聚合、避障以及定向运动。同时序参量也能够说明在一开始,群体处于比较无序的状态,而后迅速向有序过渡,在避障过程中由于需要部分无人艇调整,所以群体的序参量又迅速下降,符合群体行为本身。
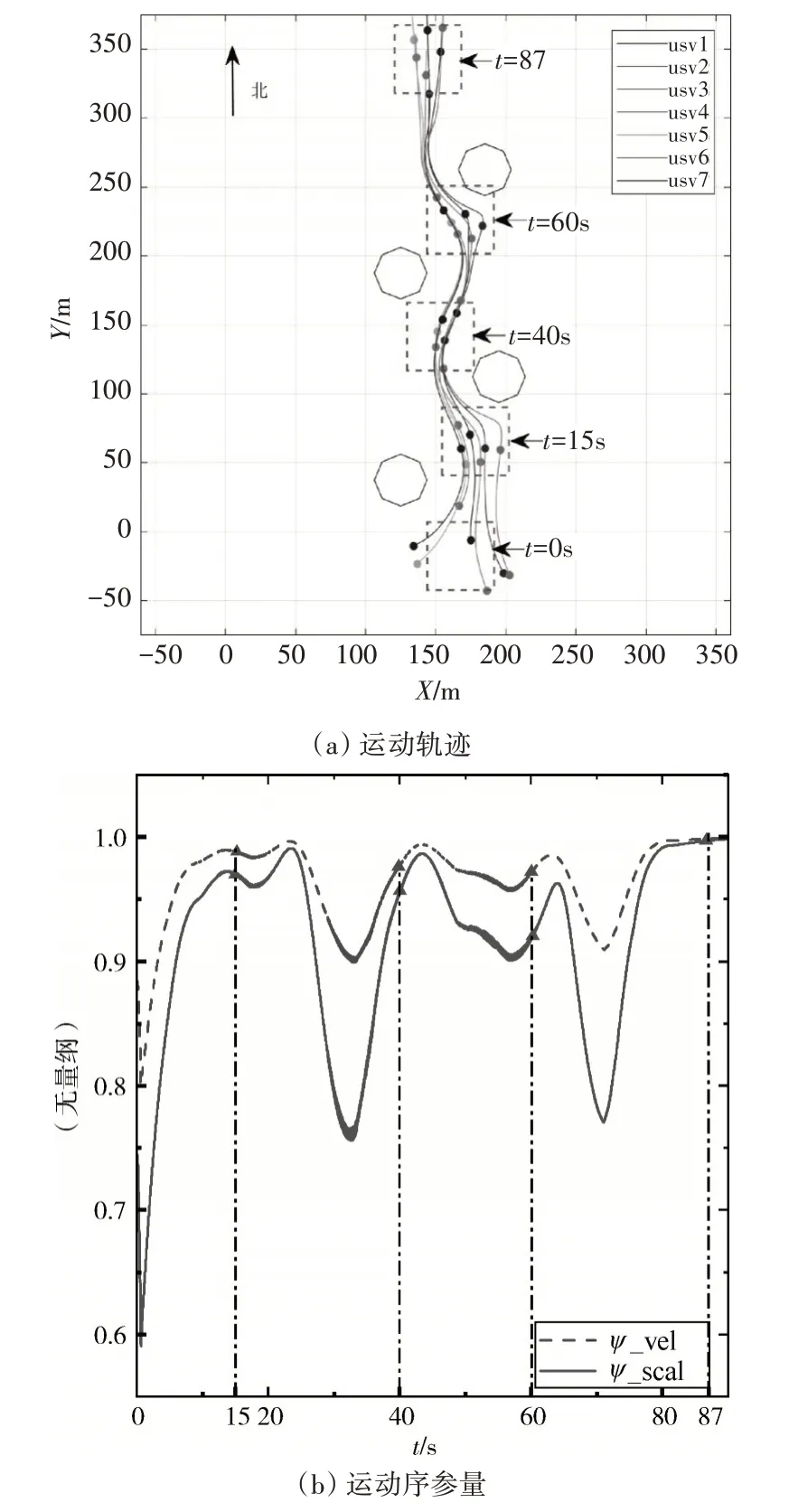
图4 设置7艘无人艇定向集群运动
实验二选择11 艘无人艇做定向的集群运动实验,其余条件与实验一相同,以验证该控制结构的可扩展性,仿真结果如图5。可以看出在无人艇数量增加后,仍可顺利完成集群运动,该分散式集群运动控制结构有较好的可扩展性。
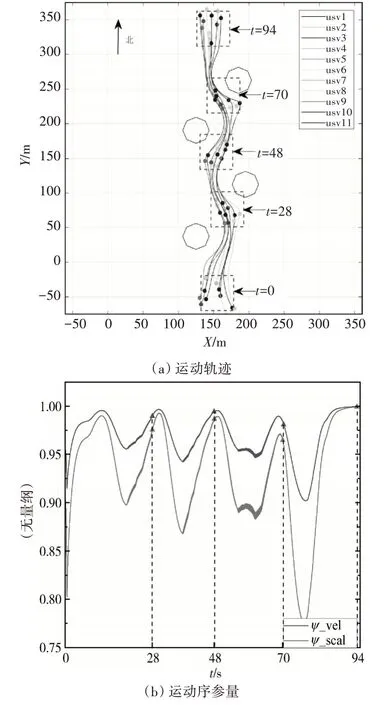
图5 设置11艘无人艇定向集群运动
实验三选择7 艘无人艇做定点集群运动,其中设置5个目标点,其坐标为target1=[330,107]m,target2=[83,236]m,target3=[67,95]m,target4=[141,74]m,target5=[150,150]m,仿真结果如图6 所示。从仿真结果看出无人艇群从t=0开始聚合并向第一个目标点移动,期间顺利实现避障;集群运动到达第一个目标点后依次访问之后的目标。结合性能指标可以看出整个集群运动过程中在密集水面障碍物水域环境下,分散式控制的无人艇集群运动可以完成迅速集结,每艘无人艇航迹稳定无明显振荡,具有较强的灵活性。
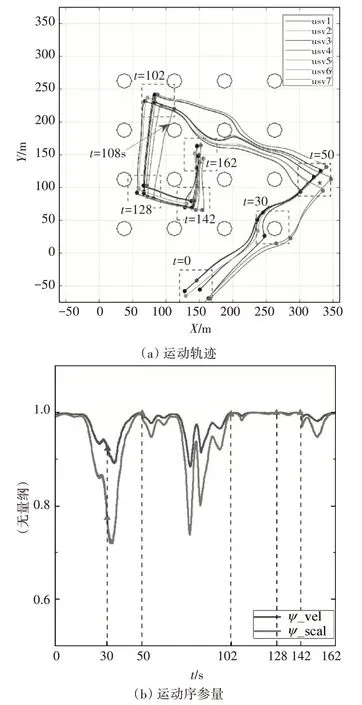
图6 多无人艇定点集群运动
6 结语
本文采用了一种分散式控制结构对多无人艇集群运动进行约束控制,引入软控制的概念,使得每艘无人艇像鸟一样只需要掌握局部信息,在局部其它艇的影响下便可完成集群运动,扩展性较强。该控制系统不像集中式和分布式控制一样存在中心控制器,无人艇之间可以交换信息,但不直接发送或者接受命令,这样的控制结构可以降低无人艇自身复杂程度和造价,且不会因为主控制单元的意外损毁而破坏整体的控制功能,具有较好的抗损毁能力。
仿真实验表明该分散式控制系统可以有效控制多无人艇定点、定向的集群运动控制,且无人艇的路线比较光滑,有一定的抗振荡和抵御外界不稳定因素的能力。且能够在复杂水域中完成集群避障任务后迅速收缩至fence 内,具有快速集群的优点。
但该系统也存在不足之处:在地形较为复杂且集群速度较快情况下,某些无人艇可能会因为局部速度调整项导致被“过度裹挟”向前运动,短程斥力不足以抵消这些艇向前惯性导致突破碰撞极限。下一步尝试加入于地形、无人艇数量以及集群速度相关的自适应参数。

