红外热成像折转光学系统的光轴静态敏感度分析

杨 丹，金 宁，杨开宇，李 晶，董树林，胡健钏，李晓君

红外热成像折转光学系统的光轴静态敏感度分析

杨 丹1，金 宁1，杨开宇1，李 晶1，董树林1，胡健钏1，李晓君2

（1. 昆明物理研究所，云南 昆明 650223；2. 空装成都局驻昆明地区军代表室，云南 昆明 650223）

红外热成像折转光学系统在复杂环境条件下，光轴容易因为光学元件的偏心或倾斜而发生漂移，影响系统对目标的指示精度。在红外热成像系统设计之初对光学系统开展光轴静态敏感度分析，能够识别出光学系统的敏感点，为满足光轴稳定性的结构优化设计提供约束条件。通过基于旋转矩阵的坐标变换，建立了光学元件旋转过程量和倾斜状态量的转换关系，从而实现了光学元件在任意方向倾斜的空间姿态模拟，确保了光轴敏感度公差分析中的蒙特卡罗采样与结构设计的约束条件相对应，并在此基础上搭建了对红外折转光学系统光轴静态敏感度分析的流程，编制了程序。用所编程序对某典型红外热成像折转光学系统进行实例分析，根据光轴稳定性的指标要求，依次对光学系统中各光学件的偏心量和倾斜量进行了光轴的灵敏度和反灵敏度分析，得出了初始公差限，再针对初始公差限数据进行了任意方向采样的蒙特卡罗分析，最终得出了各光学元件能够满足光轴稳定性指标的偏心和倾斜公差限数据，通过建立多重坐标系的方法验证了所得数据的准确性，为指导光机热优化设计奠定了基础。

红外折转光学系统；光轴漂移；静态敏感度；公差分析；蒙特卡罗采样

0 引言

红外热成像系统工作在较为严酷的使用环境中时，受安装力、高低温和冲击振动等因素影响，内部的机械支撑结构产生微小的变形，使光学元件出现空间状态的偏移（包含偏心或倾斜），导致系统的光轴发生漂移，影响系统对目标的指示精度[1-6]。红外折转光学系统具有体积小、布局紧凑的优势，但在工程实践中发现，相较于直线形光学系统，光轴在环境影响下的漂移量相对更大。为了满足使用要求，光轴的最大漂移角度即光轴稳定性必须限定在允许范围之内。因此，在系统设计阶段，需严格分析各光学元件的偏移误差对系统光轴带来的影响，识别出光学系统在静态下的敏感点，同时基于光轴稳定性指标分析出各个镜片偏心和倾斜的合理公差限，从而能够得到光学系统所容许各支撑结构件最大的形变范围，以作为结构优化的约束条件[7-14]，为光轴稳定性的设计提供指导。

对于折转光学系统，由于其非旋转对称性，光学元件的偏移状态需要考虑偏移量和偏移方向两方面信息。也就是说，在分析某个元件允许的最大偏心量或倾斜量时，需要对所有可能的偏心方向或倾斜方向进行采样，选取最严苛的情况作为结构优化的约束。国内外有关光学系统公差灵敏度的研究，在考虑元件的偏心量或倾斜量时大多仅针对-轴方向或-轴方向进行采样，而极少考虑其他倾斜方向，对折转光学系统的适用性较低[15-17]。

目前主流的光学软件具有完备分析公差的流程，但其对光学元件倾斜状态的建模是先后绕、、各个坐标轴的旋转形成，其旋转值为过程量，不能代表旋转后形成的空间状态量[18-19]。利用现有软件进行公差分析时，只能完全按照建模的输入方式，对光学元件旋转过程量采样，无法对其倾斜的空间状态量采样；而对结构优化来说，所需的约束条件为状态量，这就导致采样结果与约束条件不能对应，对结构设计的指导存在局限性。

本文基于公差分析的思想，立足于红外折转光学系统元件的偏心、倾斜静态公差，建立光学元件旋转过程量与旋转形成的空间状态量（即倾斜量和倾斜方向）之间的转换关系，实现对光学元件在任意方向倾斜状态的准确采样；在此基础上，建立光学元件偏移对光轴稳定性的影响的灵敏度分析、反灵敏度分析及蒙特卡罗分析整个公差计算流程，以获得折转光学系统的静态敏感点、以及结构优化设计所需的约束条件。

1 光学元件旋转过程量和倾斜状态量的转换关系建立

蒙特卡罗公差分析是光轴静态敏感度分析中最为重要的一步，是最终获得光学系统中各镜片偏心和倾斜合理公差限的必要过程。在红外折转光学系统光轴敏感度公差的蒙特卡罗分析中，为了和结构优化设计能够对应，需在每个元件垂直于光轴的参考平面的360°所有方向上，对倾斜量进行蒙特卡罗采样，然后根据采样的状态构建出对应的倾斜模型，从而能够对该模型进行非顺序光线追迹，计算出光轴的最终漂移情况。

对倾斜模型的构建，需要通过旋转元件来完成。在几何空间中，每个元件自带一个右手局部坐标系-，其中-轴沿光轴方向。元件的旋转运动姿态采用欧拉角来表述，旋转后的最终姿态除了与角度相关，还与旋转顺序相关[20]。在对元件的倾斜进行建模时，假设旋转按图1所规定的顺序，即元件先绕自身坐标轴的-轴左旋角度，再绕旋转后形成的坐标轴的-轴左旋角度，再绕旋转后形成的坐标轴的-轴右旋角度，得到元件的新坐标系-111，则空间中某点在原坐标系-和新坐标系-111中的坐标描述对应关系为：

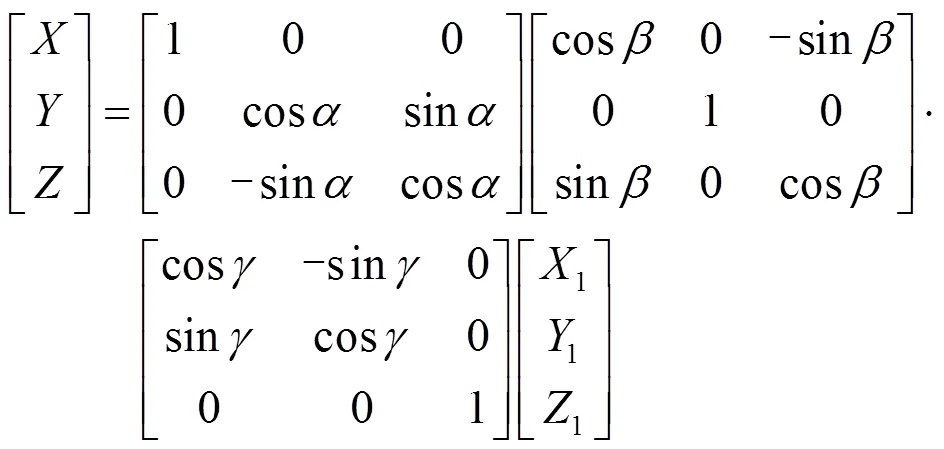
式中：[X,Y,Z]是点W在原坐标系O-XYZ中的坐标，[X1,Y1,Z1]是点W在旋转后坐标系O-X1Y1Z1中的坐标。

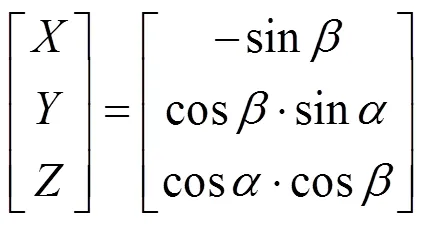
由于-轴为元件的光轴方向，因此绕-轴的旋转并不影响方向向量最后的朝向，所以由式(2)可以看到，方程组是一个与无关的等式。

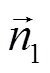
如果要实现任意方向倾斜采样的蒙特卡罗分析，需要建立光学元件旋转过程，和空间状态量的，之间的转换关系。因此联立式(2)与式(3)，得到了，与，之间的对应关系：

这样，通过旋转矩阵的推导，解出了光学元件倾斜状态量（方向角、倾斜角）到倾斜建模过程量（旋转角，）的转换对应公式。在任意方向蒙特卡罗分析中，只需对方向角和倾斜角进行采样，就可利用上述公式将采样数据转换建模需要的旋转角，，从而构建出元件倾斜的模型，进行非顺序光线追迹。

2 光轴静态敏感度分析流程构建

2.1 基本思路

对红外折转光学系统光轴静态敏感度分析，本质上是公差分析，需将光学元件的偏心、倾斜公差引入光学系统中，分析由元件偏移引起的光轴漂移与光轴稳定性指标的匹配情况。构建红外折转光学系统的光轴敏感度公差分析流程的基本思路如图3所示，输入为光学系统的仿真模型以及系统的光轴稳定性指标，经过光轴敏感度分析以后，最终输出的是光学系统中各个元件合理的公差限数据。该思路对光轴敏感度分析分解为三步：灵敏度分析-反灵敏度分析-蒙特卡罗分析[21]，每一步的分析需要基于上一步分析的结果数据作为输入，而输出的数据将作为下一步分析的输入。

流程中首先开展灵敏度公差分析，根据光轴稳定性指标进行初步分解，将光学系统的公差大致设定在某个范围，用非顺序建模实现对光学元件空间姿态的精确模拟，并通过非顺序光线追迹，仿真计算这些公差所造成的光轴漂移量数据（如图4所示），此数据即为各元件偏心和倾斜的光轴灵敏度数据，以此识别敏感元件。

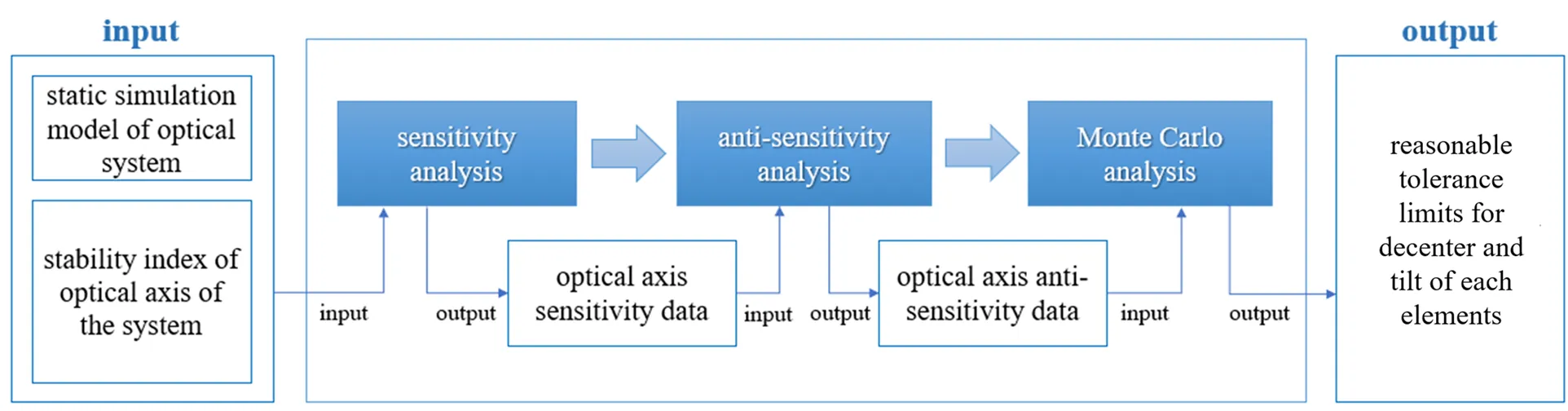
图3 构建红外光学系统光轴敏感度公差分析流程的基本思路

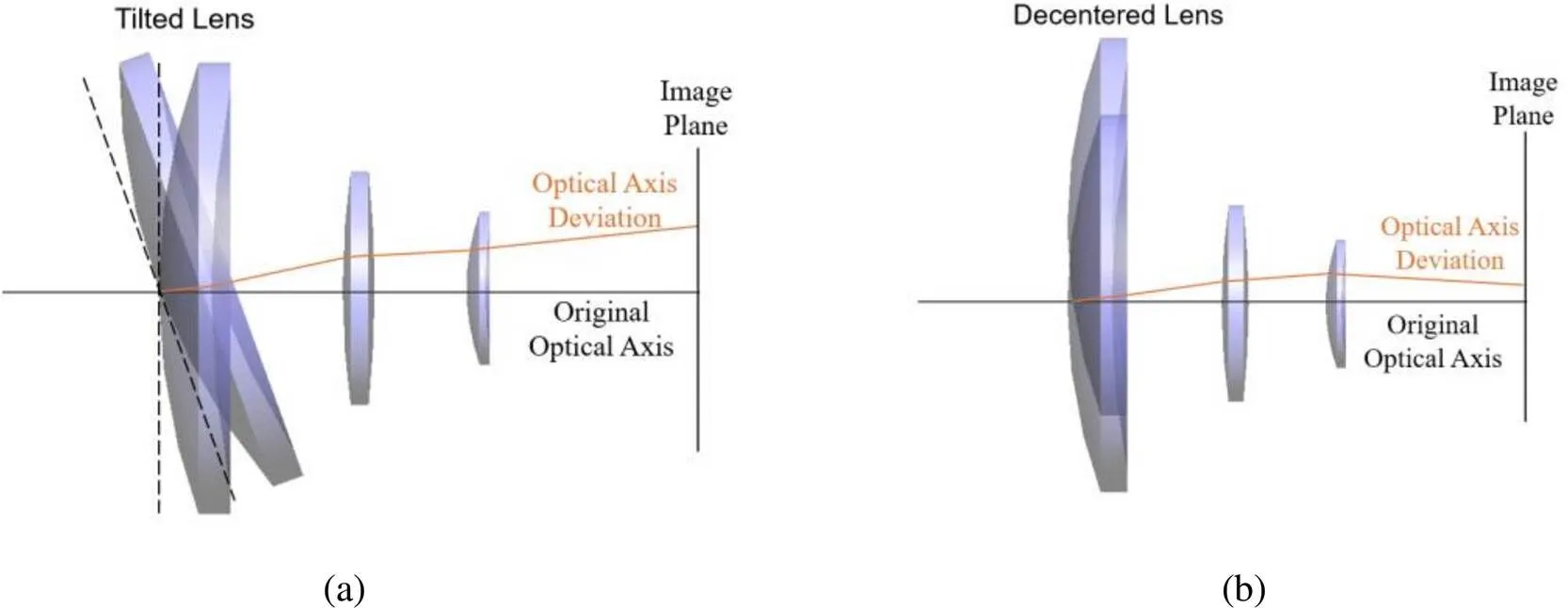
图4 透镜倾斜(a)和透镜偏心(b)引起的光轴漂移

反灵敏度分析则假设光学系统的评价标准（即光轴漂移量）变化特定的数值，评估造成相应变化的各项公差范围，称之为光轴反灵敏度数据，可根据上一步光轴灵敏度数据的多次计算迭代求得。

光轴的反灵敏度数据，可作为蒙特卡罗公差分析中的输入，即各光学件偏心和倾斜的光差限初值，以公差限初值作为反射镜各运动分量的蒙特卡洛采样区间，在区间内进行各元件偏心和倾斜随机取值并叠加成组合误差，进行了蒙特卡洛分析，得出光轴漂移量的初步统计评估结果，与系统的光轴稳定性的指标要求对比后，放宽或收紧采样区间，进行多轮分析，最终得到合理的公差限。

2.2 程序设计

根据上述思路，对光学系统进行光轴敏感度分析的程序流程如图5所示，基于Matlab编制计算程序，通过调用LightTools软件实现光学元件偏移及非顺序光线追迹，从而完成光轴漂移仿真数据计算。该流程以光学系统的光轴稳定性指标axis作为流程输入，以光学系统中各镜片的偏心和倾斜合理公差限为输出。

程序中，调取各透镜的原始偏心值0和原始倾斜值0，分别叠加标准偏心值stan和标准倾斜值stan，通过对轴上主光线追迹计算光轴漂移，并进行公差分析，得到光学元件的灵敏度数据。基于光学元件的灵敏度数据和系统的光轴稳定性指标axis，计算出光学元件的反灵敏度数据。基于光学元件的光轴反灵敏度数据，得到公差限初值0，即光学元件各运动分量的蒙特卡洛采样区间。给定循环次数loop，在公差限初值范围内对每一光学件的偏心方向，偏心量，旋转方向，旋转量四个值分别产生loop组随机数。偏心方向和旋转方向在0～360°的范围内采样，偏心量和旋转量则在公差限初值的范围内采样。由偏心方向，偏心量，旋转方向，旋转量四个值，通过上节中的数据变换，计算得出光学元件建模所需的过程量输入，即沿-轴方向的平移量，沿方向的平移量，绕-轴的旋转量，绕-轴的旋转量。

，与，的对应关系可由简单的三角函数求得：

式中：u，v与a，b的对应关系由上节中推导得出的光学元件旋转过程量和倾斜状态量的转换关系式(4)求得。

基于计算得出的位置与旋转角度输入，进行光学元件偏移状态的建模和光轴漂移的仿真分析，得到各光学元件偏心与倾斜随机采样数据搭配后的光线输出数据，对输出数据进行统计分析，得出光轴漂移量的蒙特卡洛分析结果。

将输出的蒙特卡罗分析结果与光轴漂移量的指标要求进行对比，得出新一轮蒙特卡罗分析的公差限调整系数P+1，如下式计算：

P+1＝axis/I(6)

式中：I为本轮光轴漂移量蒙特卡洛分析结果。若P+1已接近1，则说明输入的公差限已经合理，无需再调整。否则，则需按照下式放宽或收紧公差限：

+1＝P+1×(7)

式中：为本轮的公差限；+1为新一轮公差限。获取新一轮公差限后，再次展开蒙特卡罗分析，重复迭代此过程，直至公差限调整系数接近1，即光轴漂移量的蒙特卡罗统计结果与系统光轴稳定性指标要求接近，则可将该轮的公差限作为光学元件偏移的约束值。

3 光轴敏感度分析实例

根据上述搭建的光轴敏感度分析流程和计算程序，选取了光轴较为敏感的某型红外热成像光学系统作为分析对象，光学系统的仿真模型如图6所示。该系统为制冷型中波热像仪，为减少体积，采用了两个折转反射镜形成U型折转光路。本例以系统的光轴稳定性指标axis≤0.25mrad为例，对系统中8个光学透镜和2个折转反射镜的倾斜和偏心的公差限进行分析计算。

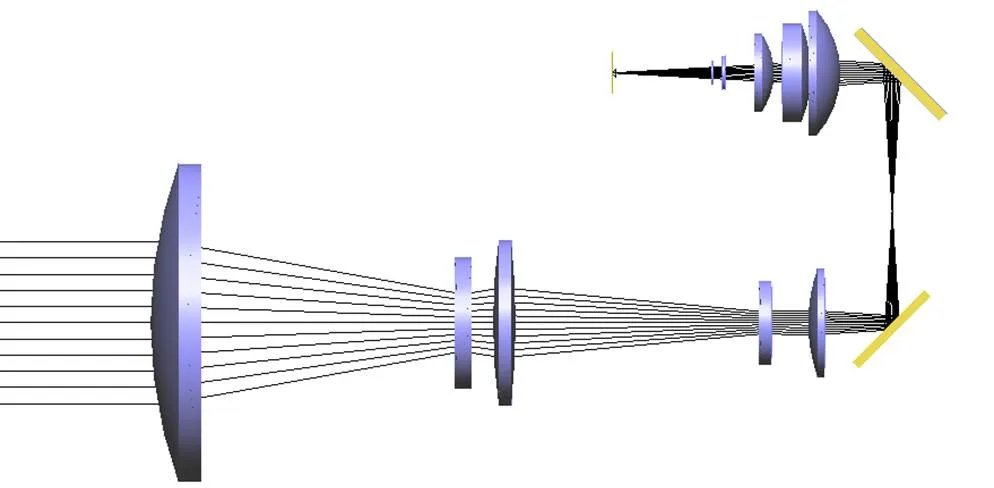
图6 光学系统的静态仿真模型

在倾斜和偏心的灵敏度分析中，本例的标准偏心值stan设置为0.01mm，标准倾斜值stan设置为0.01°。在倾斜和偏心的反灵敏度分析中，由于系统的光轴稳定性指标axis≤0.25mrad，而光学系统中包括反射镜在内，共有10个光学件，且每个光学件包含两个公差（偏心和倾斜），这样一来，共由20个公差对光轴漂移产生贡献，因此，将0.25mrad的指标均分成20份，以光轴漂移量为0.0125mrad作为反灵敏度分析的标准。

图7(a)为倾斜灵敏度分析结果，横坐标是光学元件的序号，纵坐标是光轴漂移量；图7(b)为倾斜反灵敏度分析结果，横坐标是光学元件的序号，纵坐标是光学件的倾斜量。从倾斜灵敏度折线图中可以较为直观地看出，当每个透镜同时倾斜0.01°，对光轴漂移量产生的贡献存在很大差异。对比倾斜灵敏度折线图与倾斜反灵敏度折线图中可以发现，倾斜反灵敏度的数据与倾斜灵敏度数据正好相反，第2反射镜的倾斜灵敏度最高，倾斜反灵敏度最低，第5透镜的倾斜灵敏度最低，倾斜反灵敏度最高。从图中能够识别出，第1反射镜和第2反射镜是对倾斜最敏感的关键元件。

图8(a)为偏心灵敏度分析结果，横坐标是光学件的序号，纵坐标是光轴漂移量；图8(b)为偏心反灵敏度分析结果，横坐标是光学件的序号，纵坐标是光学件的偏心量。对比偏心灵敏度折线图与偏心反灵敏度折线图中可以发现，偏心反灵敏度的数据与偏心灵敏度数据同样正好相反，第2透镜偏心灵敏度最高，偏心反灵敏度最低，第5透镜的偏心灵敏度最低，偏心反灵敏度最高。从图中能够识别出，第2透镜和第3透镜是对偏心最敏感的关键元件。

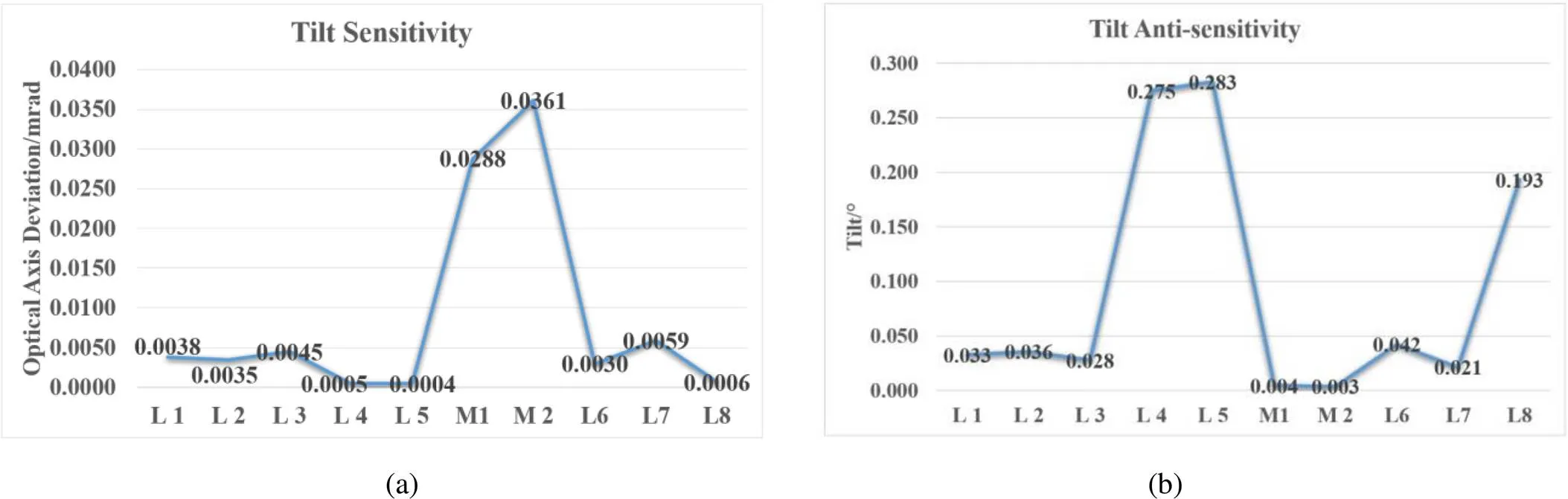
图7 倾斜灵敏度(a)和倾斜反灵敏度(b)折线图

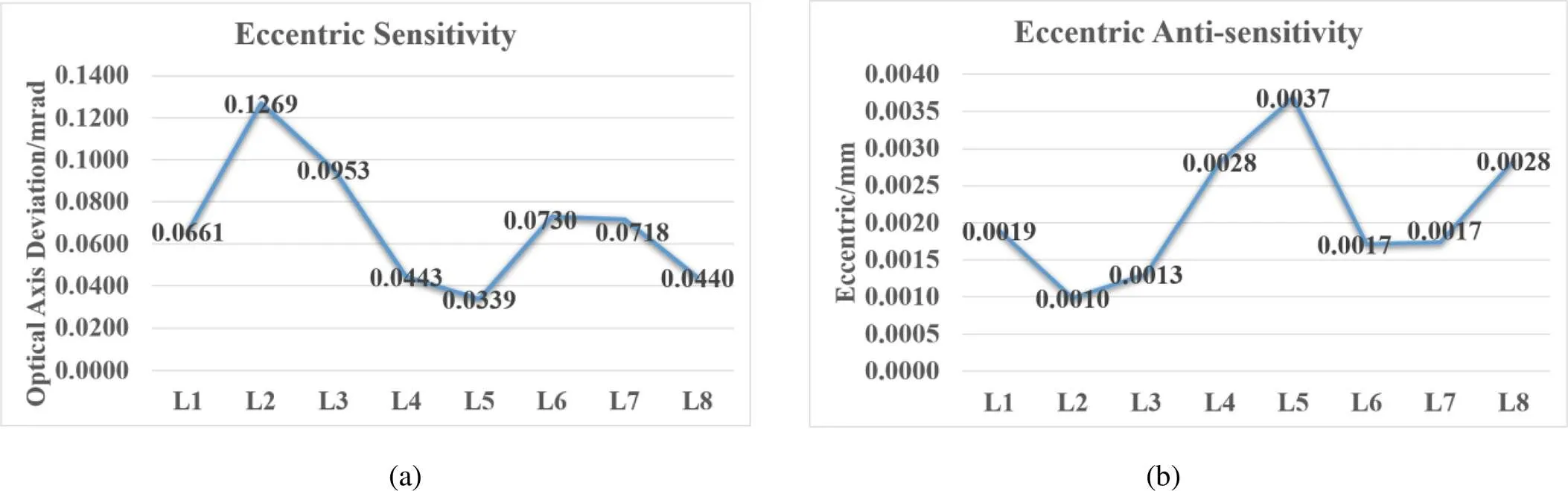
图8 偏心灵敏度(a)和偏心反灵敏度(b)折线图

将光轴反灵敏度分析数据设置为各光学元件偏心和倾斜的初始公差限，在8个透镜与2个反射镜的偏心与倾斜初始公差限范围内进行蒙特卡罗分析，本例中循环次数loop设置为10000次。图9(a)为蒙特卡罗分析后输出的10000组光学系统光轴漂移量数据的分布区间直方图，横坐标为光轴漂移量，纵坐标为分布在相应光轴漂移量区间的蒙特卡罗实验次数，由图可知，分布在光轴漂移量为0.021mrad附近区间的实验次数最多。图9(b)为数据的累积分布函数图，横坐标为光轴漂移量，纵坐标为累计分布概率，可以看到，50%的概率光轴移动量在0.025mrad范围内，70%的概率光轴移动量在0.033mrad范围内，90%的概率光轴移动量在0.0456mrad范围内。

本文中以90%的概率为例，因此基于初始公差限，光学系统的光轴移动量评估结果大概率分布在0.0456mrad范围内，而对比本例设置的指标，系统光轴稳定性axis≤0.25mrad。因此基于蒙特卡罗分析评估的光轴漂移量结果还远低于光轴一致性指标，说明设置的初始公差限过于保守，因此按照式(6)计算，公差调整系数等于5.48，并按照式(7)放宽各光学件的偏心与倾斜公差限。

根据调整后的公差限，进行蒙特卡罗随机采样。新一轮蒙特卡罗分析的输出数据分布区间直方图及累积分布函数图如图10(a)和图10(b)所示。

本轮输出的光轴漂移量数据以90%的概率分布在0～0.256mrad范围内，基本与光学系统的光轴一致性指标相匹配。因此将本轮输入的公差限作为最终各光学件的倾斜和偏心合理公差。

表1为采用本文程序对目标光学系统依次进行了灵敏度分析、反灵敏度分析、蒙特卡罗分析之后，得出的各个光学元件的合理公差限。此公差限可作为结构优化设计的约束条件，只要由结构件引起的光学元件偏心和倾斜不超过表1数据的范围，即可保证光学系统的光轴漂移量不超出系统光轴稳定性0.25mrad的指标要求。从表1数据和前面灵敏度、反灵敏度分析结果可以看出，结构优化设计需要着重考虑高低温或外力的作用下，第1、2反射镜的倾斜、以及第2、3透镜的偏心。因此，该分析识别出了光学系统的敏感点，同时能够指导结构优化设计，以满足光轴稳定性指标。

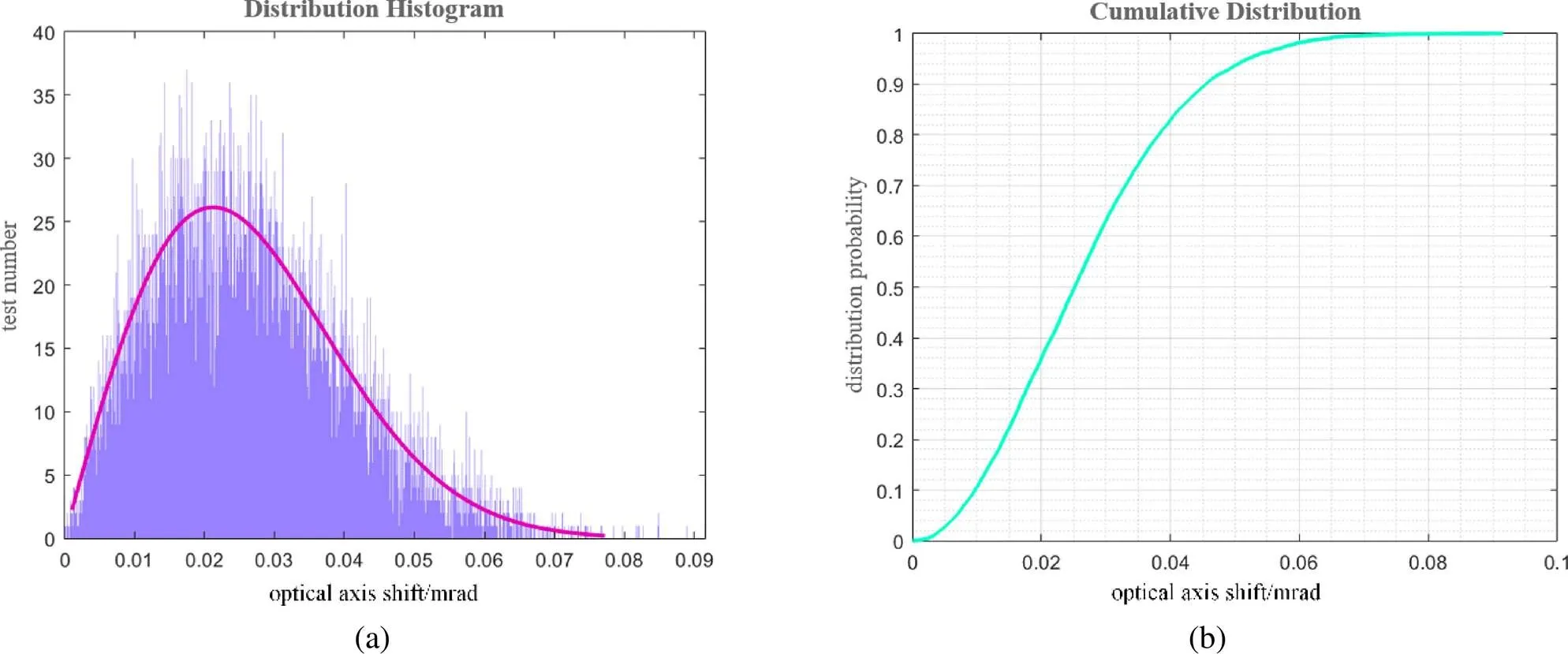
图9 光轴漂移量分布直方图(a)和累积分布图(b)

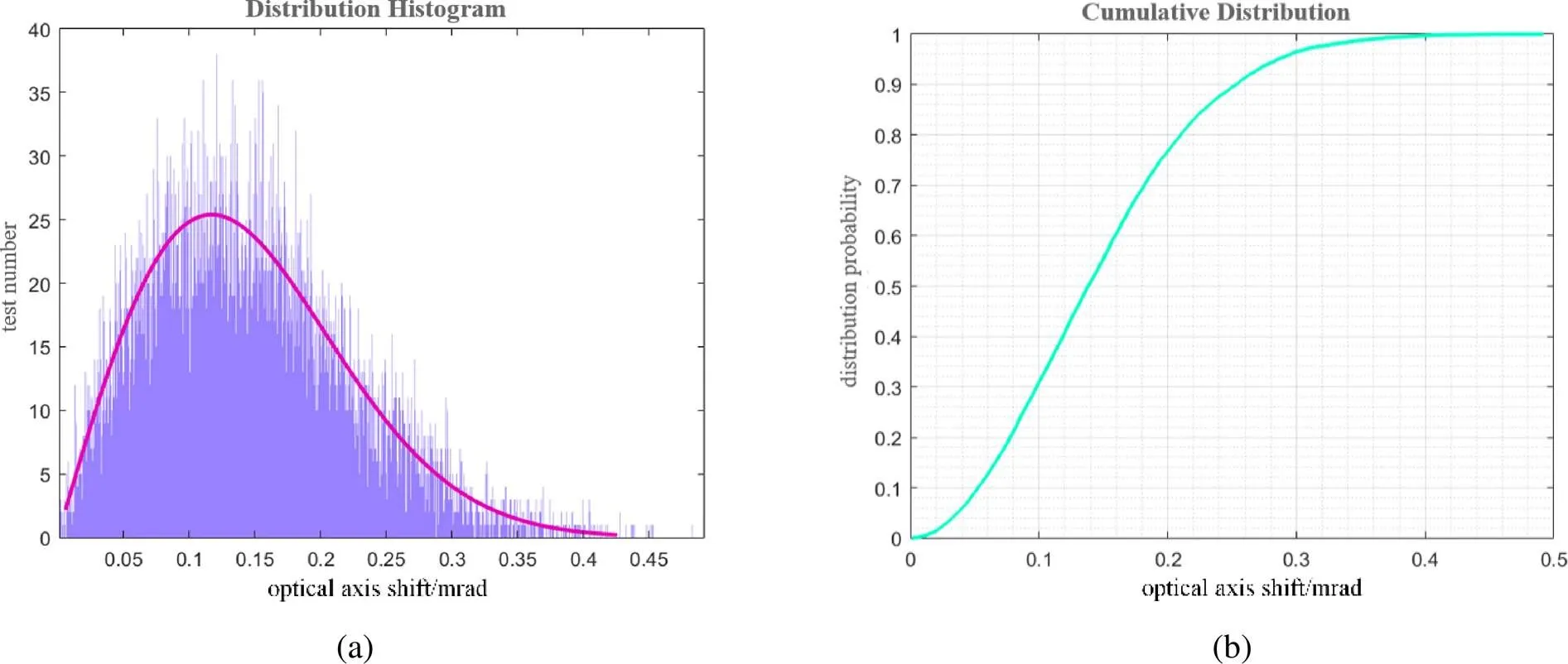
图10 调整公差限后的光轴漂移量分布直方图(a)和光轴漂移量累积分布图(b)

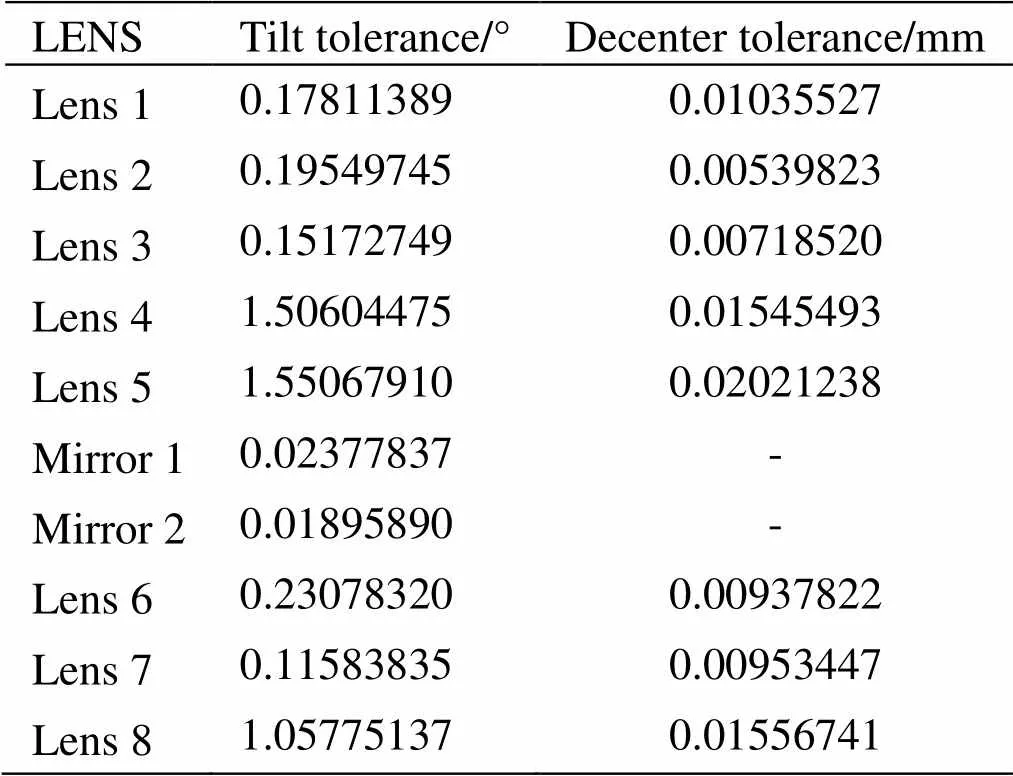
表1 各光学件倾斜与偏心最终公差限

4 数据准确度验证

本文为实现任意角度倾斜的蒙特卡罗分析，采用数据转换的思路，利用坐标变换推导出了方向角和倾斜角到旋转建模角度的转换关系式。为了对文中角度转换公式的准确性进行验证，利用上一章实例中输出的公差限，并通过上文中提到的通过手动建立多重临时坐标系的替代方法，对实例中光学系统再次进行蒙特卡洛分析，观察是否能得出一致的光轴移动量分布数据。

在仿真软件中，如图11所示，根据每一个光学元件的原始坐标系分别建立一个相同的临时坐标系，并使临时坐标系绕¢-轴左旋90°旋转，使临时坐标系的¢-轴朝向原内层坐标系的-轴，临时坐标系的¢-轴朝向原内层坐标系的-轴，临时坐标系的¢-轴朝向原内层坐标系的-轴负方向，将原始坐标系嵌套在临时坐标系的内层并绑定，让外层坐标系带动光学元件一同旋转，实现让光学件先绕光轴旋转，在绕与光轴垂直方向的坐标轴旋转。

以实例中基于最后一轮公差限产生随机采样数据，输入到临时坐标系中，进行蒙特卡洛分析。得到的数据分布区间直方图如图12(a)，与上一章中得出的数据分布区间直方图如图12(b)进行对比，可以看出，两种方法得出的结果分布完全一致，证明了数据转换方法的准确性。

此外，相较于手动建立多重临时坐标系的方法，本文建立的方法适用性更强、效率更高，省去了很多繁琐过程，不需要为每一个新的光学系统的所有光学元件手动建立与其坐标相对应的两重临时坐标系，避免了数据输入或匹配错误。

图11 临时坐标系示意图

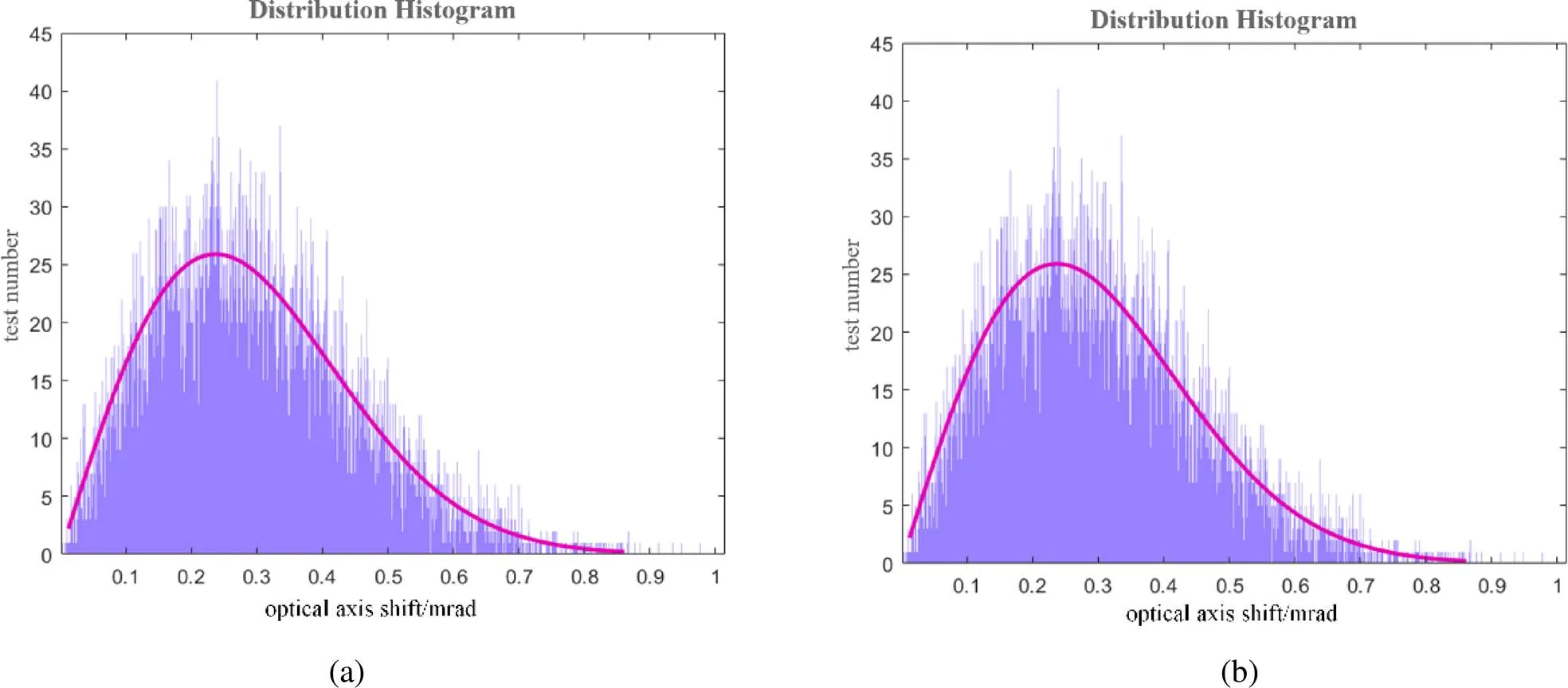
图12 数据转换方法得出(a)和临时坐标系方法得出(b)的分布直方图

5 结论

在对红外热成像折转光学系统进行光轴稳定性的结构优化过程中，非常有必要针对光学系统开展光轴的静态敏感度分析，基于系统的光轴稳定性指标分析出各个光学元件偏心和倾斜的合理公差限，从而指导结构优化。为解决蒙特卡罗分析中对折转光学系统元件的任意方向倾斜采样的难点，通过基于旋转矩阵的坐标变换，建立了光学元件旋转过程量，和空间状态量的，相互转换的方法，使蒙特卡罗分析能够模拟真实情况下的光学元件运动，计算效率高且具有通用性。在建立的数据转换方法的基础上，搭建了对红外光学系统光轴静态敏感度分析的流程，并运用Matlab对LightTools进行二次开发，实现了程序化。与此同时，以一个光轴较为敏感的实际光学系统为例，运用建立的方法对其开展了光轴静态敏感度分析，得出了光学系统的敏感点和各光学元件的合理公差限，并结合建立临时外重坐标系的方法，对数据准确性进行了验证，证实了公式推导以及程序的可靠性和准确性。

文中所建立的光轴静态敏感度分析流程为实现完整的光机热优化设计奠定了基础，它虽然是针对光学系统的光轴分析所搭建的，但与此同时，文中提出的任意方向倾斜的蒙特卡罗采样方法也为折转光学系统像质的公差分析提供了解决思路。后续将对如何优化文中方法分析出的敏感元件开展研究，以期进一步提高光学系统的光轴稳定性。

[1] 郭夏锐, 廖志波, 王春雨, 等. 光轴一致性误差对空间透射式系统像差和质量的影响[J]. 红外与激光工程, 2012, 41(2): 437-441. GUO Xiarui, LIAO Zhibo, WANG Chunyu, et al. Aberration and alignment quality investigation of space transmission optical system with centering error of optical axes[J]., 2012, 41(2): 437-441.

[2] 马宏川, 范宏波, 林宇, 等. 热像仪光机热集成分析综述[J]. 红外技术, 2019, 41(2): 134-141. MA Hongchuan, FAN Hongbo, LIN Yu, et al. Review of thermal-structural-optical integration analysis of thermal imager[J]., 2019, 41(2): 134-141.

[3] 王阳, 黄煜, 李占峰, 等. 利用恒星对天文观测系统光轴平行性检校[J].红外与激光工程, 2017, 46(5): 0517003. WANG Yang, Huang Yu, Li Zhanfeng, et al. Calibration of optical axis parallelism by using star for astronomical observation system[J]., 2017, 46(5): 0517003.

[4] 陈志斌, 肖文健, 马东玺, 等. 大间距多光轴一致性野外在线检测方法[J]. 光学学报, 2017, 37(1): 0112006.Chen Zhibin, Xiao Wenjian, Ma Dongxi, et al. A method for large distance multi-optical axis parallelism online detection[J]., 2017, 37(1): 0112006.

[5] 杨耀山, 赵泉, 王建龙, 等. 红外光学系统光轴稳定性建模与分析[J]. 电光与控制, 2017, 24(12): 82-84.Yang Yaoshan, Zhao Quan, Wang Jianlong, et al. Optical axis stability modeling and analysis of infrared optical system[J]., 2017, 24(12): 82-84.

[6] 隋杰, 程会艳, 余成武, 等. 星敏感器光轴热稳定性仿真分析方法[J]. 空间控制技术与应用, 2017, 43(4): 38-41.Sui Jie, Cheng Huiyan, Yu Chengwu, et al. A thermal stability analysis and simulation method for boresight axis of star sensor[J]., 2017, 43(4): 38-41.

[7] 董雪岩, 许方宇, 陈骥, 等. 1m红外太阳望远镜镜面位置误差致光轴偏移分析[J]. 红外技术, 2016, 38(10): 870-876. DONG Xueyan, XU Fangyu, CHEN Ji, et al. Analysis on optic axis deviation induced by lens position disorder of 1m new vacuum solar telescope[J]., 2016, 38(10): 870-876.

[8] Kalikivayi V, Kumar V C P, Kannan K, et al. Tolerance analysis of misalignment in an optical system using Shack–Hartmann wavefront sensor: experimental study[J]., 2015, 54(7): 075104.

[9] 高磊. 基于蒙特卡洛法的公差分析及优化设计方法研究[D]. 哈尔滨: 哈尔滨理工大学, 2015.Gao Lei. Research on the Tolerance Analysis Based on Monte Carlo Method and Optimal Design Method[D]. Harbin: Harbin University of Science and Technology, 2015.

[10] 刘琳, 张兴德, 贺谊亮. 基于蒙特卡洛模拟法的红外光学系统公差分析[J]. 激光与红外, 2020, 40(5): 497-499.Liu Lin, Zhang Xingde, He Yiliang. Monte Carlo simulation and its application in the IR optical system[J]., 2020, 40(5): 497-499.

[11] 袁贵星, 王平. 蒙特卡洛模拟及其在公差设计中的应用[J]. 天津科技大学学报, 2008, 23(2): 61-64.Yuan Guixing, Wang Ping. Monte Carlo simulation and its application in tolerance design[J]., 2008, 23(2): 61-64.

[12] Yang K Y, Jin N, Yang D, et al. Monte Carlo calculation on stray radiation scattered by the baffle with a heterotypic surface for uncooled infrared system[C]//, 2018, 10815: 108150R.

[13] 苏朋. 365nm光刻照明系统中变焦系统的设计及公差分析[J]. 红外与激光工程, 2022, 51(7): 20210524.Su Peng. Design and tolerance analysis of the zoom system in 365nm UV lithography illumination system[J]., 2022, 51(7): 20210524.

[14] 王川川, 岑兆丰, 李晓彤, 等. 基于线性模型的聚焦光学系统静态公差优化算法[J]. 光子学报, 2017, 46(11): 1122001. WANG Chuanchuan, CEN Zhaofeng, LI Xiaotong, et al. Optimization algorithm of static tolerance in focusing system based on linear model[J]., 2017, 46(11): 1122001.

[15] 蔡东浩, 李雅灿, 魏立冬, 等. 高光谱成像仪中曲面棱镜的装调公差研究[J]. 光学学报, 2021, 41(6): 60-68.Cai Donghao, Li Yacan, Wei Lidong, et al. Fabricating tolerance of curved prisms in hyperspectral spectrometer[J]., 2021, 41(6): 60-68.

[16] 李美萱, 董连和. 浸没式光刻照明系统中会聚镜的设计及公差分析[J]. 应用光学, 2019, 40(5): 876-881. LI Meixuan, DONG Lianhe. Design and tolerance analysis of converging lens in immersion Lithography illumination system[J]., 2019, 40(5): 876-881.

[17] 曹宇泽, 马文礼. 两步式灵敏度矩阵法在卡塞格林望远镜装调中的应用[J]. 光电工程, 2020, 47(2): 5-12.Cao Yuze, Ma Wenli. Application of two step sensitivity matrix method in Cassegrain telescope alignment[J]., 2020, 47(2): 5-12.

[18] Synopsys Inc.9.1[M]. Mountain View: Synopsys, 2020.

[19] ZEMAX LLC.21.3Version September 2021[M]//Kirkland: ZEMAX, 2021.

[20] 王增伟, 赵知诚, 杨溢, 等. 基于刚体运动完备方程的光机热集成分析方法[J]. 红外与激光工程, 2022, 51(6): 20210617.Wang Zengwei, Zhao Zhicheng, Yang Yi, et al. Thermal -structural-optical integrated analysis method based on the complete equations of rigid body motion[J]., 2022, 51(6): 20210617.

[21] 张坤, 钟兴, 孟遥, 等. 大视场纳型星敏光学系统公差灵敏度研究[J]. 光子学报, 2019, 48(5): 0522001. ZHANG Kun, ZHONG Xing, MENG Yao, et al. Tolerance sensitivity research of nano-star sensor optical system with large field[J]., 2019, 48(5): 0522001.

Optical Axis Static Sensitivity Analysis for Infrared Thermal Imaging Folding Optical System

YANG Dan1，JIN Ning1，YANG Kaiyu1，LI Jing1，DONG Shulin1，HU Jianchuan1，LI Xiaojun2

(1. Kunming Institute of Physics, Kunming 650223, China;2. Military Representative Office of Chengdu Bureau of AIR Force Stationed in Kunming Area, Kunming 650223, China)

The optical axis of an infrared thermal imaging folding optical system is prone to shift owing to decentering of the tilt of optical components under complex environmental conditions, which affects the indication accuracy of the system for the target. Static sensitivity analysis of the optical axis for the optical system at the beginning of the design of the infrared thermal imaging system is useful for identifying the sensitive points of the optical system and provides constraints for the structural optimization design to meet the stability of the optical axis. The conversion relationship between the rotation process and spatial state quantities of the optical components was established by coordinate transformation based on the rotation matrix to simulate the spatial attitude of the optical component tilted in any direction and ensure that the Monte Carlo sampling in the optical axis sensitivity analysis corresponds to the constraint conditions of the structural design. On this basis, the flow of the static sensitivity analysis of the optical axis of the infrared folding optical system was established, and a program was compiled. A typical infrared thermal imaging folding optical system was analyzed using this program. According to the index requirements of the optical axis stability, the optical axis sensitivity and inverse sensitivity of the decenter and tilt of each optical component in the optical system were analyzed, and the initial tolerance limit was obtained. Then, Monte Carlo analysis sampling could be performed in any direction according to the initial tolerance limit data; thus, the decenter and tilt tolerance limit data that meet the optical axis stability index could be obtained, and the accuracy of the obtained data was verified by establishing a multi-coordinate system. Static sensitivity analysis provides a foundation for guiding the design of optical–mechanical thermal optimization.

infrared folding optical system, optical axis shift, static sensitivity, tolerance analysis, Monte Carlo sampling

O435

A

1001-8891(2023)08-0828-09

2022-12-27；

2023-02-15.

杨丹（1991-），女，云南昆明人，工程师，硕士，主要从事光学系统设计和仿真方面的研究。E-mail：naomi626391@126.com。

杨开宇（1984-），女，云南昆明人，正高级工程师，博士，主要从事光学系统设计和仿真方面的研究。E-mail：yky20030634@126.com。

国家重点研发计划（2017YFA0701200）。