基于ANSYS的圆柱形超声工具头振幅优化设计

覃耀聪,姚 震,罗红平,何 健,高丰才

(广东工业大学,广东 广州 510006)

0 引言

超声焊接是目前生产口罩的主流方式之一[1],工具头是超声焊接系统的核心部件之一,由于口罩尺寸的影响,导致工具头的径向直径尺寸普遍在150 mm或以上,超过了对应声波波长的四分之一,工业上将其称为大尺寸工具头。大尺寸工具头在超声焊接过程中会产生耦合振动,导致工具头工作面振幅均匀度降低[2],而振幅是影响焊接质量的重要工艺参数[3],振幅过小会导致工件虚焊,振幅过大则会导致工件烧伤[4]。目前工业上设计大尺寸圆柱体工具头时更多的是依赖以往的设计经验,通过实验、仿真多次修改工具头尺寸,最终达到生产要求,设计周期长且振幅均匀度不理想。

目前,对大尺寸圆柱体的振动分析研究取得了一定进展,如:荣森司等[5]提出了表观弹性法并用于分析大尺寸圆柱体的振动特性;梁明军等[6]根据表观弹性法使用有限元软件分析了耦合系数在圆柱体中的分布规律,并给出了耦合系数、材料泊松比、振动模态三者间的关系;梁召峰等[7]在表观弹性法基础上引入等效机械阻抗概念,提出了大尺寸圆柱形开槽工具头的频率设计公式;杨琨[2]根据频率公式在有限元软件中初步仿真探索了开槽与工具头频率、振幅的关系;Liu等[8]根据机电等效电路分析了大尺寸中空圆柱体的共振频率。

上述研究表明,人们对大尺寸圆柱体的振动特性已逐渐明晰,但目前应用于实际口罩生产的研究并不多。因此本文根据已有的研究并结合有限元法提出一种基于Ansys的超声工具头的振幅优化思路,旨在提高工具头振幅均匀度进而提高口罩焊接质量。

1 大尺寸圆柱工具头初步设计

对于大尺寸的振动体常见的振动控制方法有:开槽、开狭缝、设计附加弹性体[2]。由于开槽的生产成本和难度要低于其余两者,故采用开槽设计。

根据前人对开槽圆柱体与表观弹性法的研究[2]:

(1)

(2)

(3)

(4)

(5)

(6)

式中,A′代表开槽后的等效面积,n代表开槽数目,w代表开槽宽度,E代表材料杨氏模量,ρ代表密度,r′代表中间部分开槽后的等效半径,ω代表角频率,Ez1代表圆柱形振子的基频轴向表观弹性模量,Ez2代表开槽后等效圆柱振子的基频轴向表观弹性模量,kz1代表h1、h2部分等效纵振的波数,kz2代表开槽后等效圆柱振子的h1、h2部分等效纵振的波数,k代表中间开槽部分单个圆柱体纵振波数,R值由材料泊松比确定[9]。

现设计一直径为180 mm,工作频率在15 kHz附近,材料为7075铝合金的圆柱形工具头。由于上端面要预留一定深度的螺栓孔用于连接变幅杆与工具头,故取上端面高度h1=20 mm。下端面为工作面,为减少轴向尺寸节约生产成本,故暂取下端面高度h2=10 mm。综合考虑生产成本与加工难度,暂取槽数n=6,槽宽w=8 mm。

由式(1)-式(6)计算可得,未优化的开槽工具头总高度L=163.8 mm,取L=160 mm。

2 有限元分析

2.1 模态分析

使用Ansys Workbench中的模态分析系统对前述工具头进行模态分析。圆柱体最大几何尺寸在180 mm,故先将单元网格尺寸设置在8 mm,采用六面体主导的划分方法。

圆柱体工具头设计谐振频率为15 kHz,故设置搜索范围限制在14～16 kHz,搜索限制范围内的10阶模态,得到各阶纵振模态结果,其结果如图1。

图1 未优化开槽工具头的前四阶模态分析结果

由图1可知,一阶模态以纵振为主,符合设计需求,对应频率为15066 Hz,与设计目标相差66 Hz,误差在1%以内,其余模态有明显的径向振动,不符合设计需求。由于式(6)计算结果受到多个参数影响,同时泊松比υ对应的R值解为数值解,存在一定误差性,故认为仿真结果的误差在合理范围内,具有较高的可信度。

2.2 谐响应仿真优化设计

在大尺寸圆柱形工具头初步设计中,工具头的开槽参数、下端面高度为粗略取值,存在优化空间。因此使用Ansysy Workbench中的谐响应分析模块分别对圆柱形工具头的开槽参数、下端工作面高度进行单因素仿真分析,求解工具头纵振频率、纵振变形均值等数据,以分析各个结构参数对工具头振幅的影响,从而得出较优解,同时找出影响振幅均匀度的关键因素。

在实际工作中,工具头主要在自身与变幅杆的连接面处接收来自变幅杆的正弦振幅激励,故对圆柱体上端面的凹坑施加一个垂直于该面的100 μm位移激励,由于仿真输入的激励源为位移,故采用完全法求解。

以纵振极大值与极小值之差、纵振均值衡量振幅均匀度,则基于该工具头的结论如下:

1)由图2可知工作面高度增加,振幅均匀度增加;

图2 以工作面高度为变量开槽工具头仿真结果 图3 以中间槽高度为变量开槽工具头仿真结果

2)由图3可知随着开槽高度变化对振幅均匀度的影响较小;

3)由图4可知开槽数目对于控制振幅均匀度存在最优解,数目为6或8时振幅均匀度较好;

图4 以槽宽为变量开槽工具头仿真结果 图5 以开槽数目为变量开槽工具头仿真结果

4)由图5可知槽宽为10 mm或12 mm的工具头振幅均匀度表现较好。

综上取圆柱体优化后开槽工具头结构参数如下:开槽数n=6,槽宽w=10 mm,两端高度h=20 mm,半径r=90 mm,总高度L=160 mm。

2.3 谐响应仿真对比

由耦合振动理论可知,径向尺寸和轴向尺寸比值φ越大的圆柱体工具头纵振时的径向振动越明显,意味着振幅均匀度越差。为验证该工具头设计方法的有效,取一现有半径r=80 mm,总高度L=151 mm,其径轴比φ=D/L=1.067的无开槽结构工具头与优化前后的开槽工具头比较,谐响应仿真激励设置为100 μm,易知圆柱体开槽工具头径轴比φ=1.125。从理论上来说径轴比较小的无开槽结构工具头振幅均匀度应该优于径轴比较大的开槽工具头。谐响应仿真结果如表1、图6所示。

表1 各工具头谐响应仿真结果对比

图6 各工具头谐响应仿真结果(单位:μm,负号代表方向)

以纵振差值衡量工具头工作面振幅均匀度,该值越小,表示工具头振幅均匀度越好。

由表1可知:

1)虽然开槽工具头径轴比大于无开槽结构工具头,但开槽工具头纵振差值远小于无开槽结构工具头,且振幅均匀度表现较好,表明该方法设计的工具头有效;

2)对比开槽工具头优化前后的结果可知,工具头经过结构优化后,虽然纵振频率有所下降,但振幅均匀度进一步提升。

3 实验测试

为进一步验证该工具头设计方法的可行性,取优化后开槽工具头、无开槽结构工具头做对比实验,实验平台如图7所示。

图7 两个工具头实物照片

3.1 振幅测试

在工具头工作面上确定三个不同的方向,确定三个不同直径的圆,取方向线与圆的交点作为采样点,采样位置如图8。

图8 采样点确定方法 图9 实验平台

使用激光测振仪检测工具头测量采样点上的振幅,观察工具头振幅趋势是否符合仿真结果,实验设备如图9。

实验结果如表2和表3,各工具头振幅均值对比如图10。

表2 无开槽结构工具头(直径160mm)纵向振幅测试结果

表3 优化后的开槽工具头(直径180mm)纵向振幅测试结果

图10 工具头振幅均值对比

由工具头振幅均值对比可知,直径为180 mm优化后的开槽工具头在测量跨度、径轴比皆大于直径160 mm无开槽结构工具头的情况下,振幅均值变化幅度前者要小于后者,这表明利用该方法设计所得的工具头振幅均匀度要优于传统工具头。

3.2 焊接测试

由于工具头工作面的振幅均匀度对焊接质量有重要影响,为进一步验证该方法设计的工具头是否对焊接质量有所改善。在其余焊接条件相同的情况下(负载压力为0.7 MPa,焊接时间为0.5 s),对优化后的开槽工具头、无开槽结构工具头进行口罩焊接实验。

焊接多个口罩,取多个测试样品(图11)用于断裂拉力测试,夹持部位如图12所示,取样方式如图13所示(剪取图中画圈部分作为测试样品),拉力测试平台如图14所示。以多个样品的断裂拉力峰值分布情况衡量焊接质量优劣。

图11 断裂拉力测试样品 图12 夹头夹持部位示意图

图13 焊接的取样口罩 图14 断裂拉力测试平台

断裂拉力测试结果如图15。

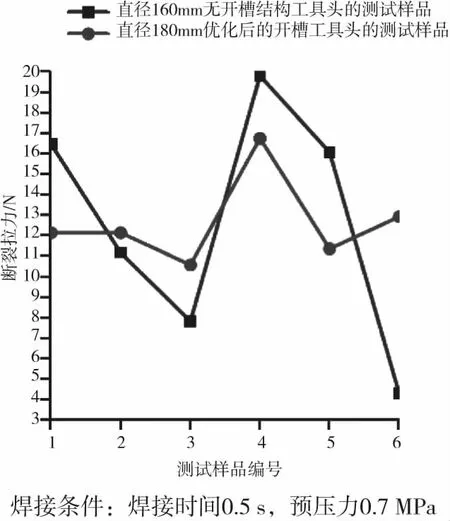
图15 断裂拉力测试结果

由图15可知,优化后的开槽工具头样品的断裂拉力值波动范围小于无开槽结构工具头,且数值均维持在10 N以上。虽然无开槽结构工具头样品的断裂拉力最大值能够达到20 N左右,但最小值也接近4 N,波动范围较大,表明焊接质量不稳定。由此可得,同样焊接条件下,优化后的开槽工具头焊接口罩的一致性要优于无开槽结构工具头。

4 讨论

对根据表观弹性法和有限元分析设计所得的工具头,分别进行了仿真模拟、振幅测试、焊接测试,根据结果分析得到的结论如下:

1)相对于根据传统经验设计的工具头,结合表观弹性法、有限元法设计的工具头振幅均匀度表现更好;

2)通过有无开槽结构的工具头振幅测试、焊接实验对比,工具头振幅均匀度改善能够提高焊接样品质量的一致性。

上述结果表明由表观弹性法与有限元法结合设计所得的工具头具有可行性,该方法设计所得的工具头对比传统工具头,在振幅均匀度、产品焊接质量上均有所改善。