型线偏置对涡旋压缩机动盘尺寸和动力学特性的影响

程军明，王 澈，张 帅，赵子博，吴建华

（1.广东美的环境科技有限公司，广东顺德 528300；2.西安交通大学 能源与动力工程学院，西安 710049）

0 引言

涡旋压缩机在车用、家用和商用制冷系统中得到了大量应用。在安装空间受限和舒适性的要求下，对压缩机尺寸、振动噪声有着更为严格的要求［1］。在此过程中，国内外学者对变壁厚型线［2］、非对称吸气［3］等方式进行了研究。研究结果表明使用变半径圆渐开线［4］、代数螺线［5］等变壁厚型线在相同涡旋盘直径时，具有更高的吸排气量、更高的内容积比和更低的泄漏线长度。采用异步非对称吸气，则需要对动静涡旋齿进行不对称修正，以减少在排气口打开时由于内容积比不相等造成的混合损失［5］，采取非对称吸气变壁厚设计的涡旋压缩机，因为更加紧凑的设计逐渐引起了众多关注。此外，虽然对型线偏置的概念早有提出［6］，但是近年来才有文献对对称型线偏置的设计过程进行研究分析［7］，该研究指出偏置能在动盘半径有限的情况下增大行程容积，但是偏置距离过大时，动盘将会出现正负自转交替变化的趋势。可以看到，公开文献对变壁厚和非对称型线［8］的研究主要集中在压缩过程的热力学上，对动盘尺寸优化和动力学过程少有涉及。尤其是型线偏置后十字滑环［9］和动盘轴向受力研究较少，影响了零部件间隙关系分析［10］和压缩机寿命提高［11］。为此，有必要对非对称变壁厚型线在偏置后的尺寸和动力学特性进行更加深入的理论研究。

为此，本文在建立的涡旋压缩机内部过程模型的基础上，推导了旋转、平移偏置对其静盘轮廓的最大半径和动盘自转力矩的影响公式，提出了动盘尺寸和动盘自转力距对偏置设计的响应曲面，以此具体分析了平移偏置使动盘半径最小时动盘和十字滑环的动力学特性，为提高涡旋压缩机的型线偏置设计和零部件受力分析提供了参考。

1 模型建立

1.1 涡旋压缩机内部过程模型

非对称涡旋压缩机工作腔及工作孔示意如图1 所示。

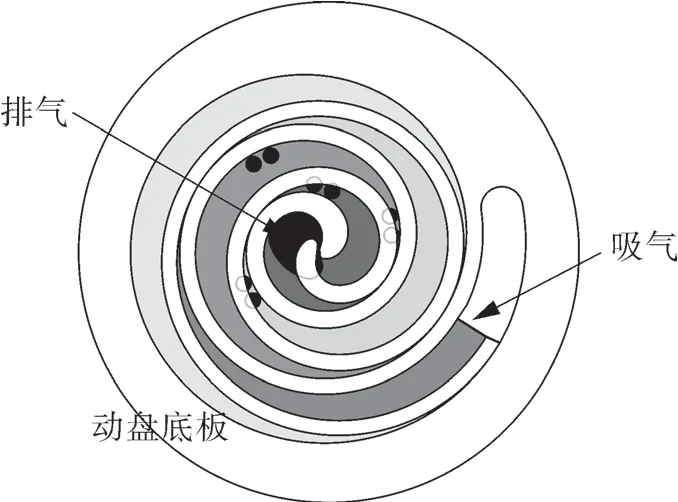
图1 非对称涡旋压缩机工作腔及工作孔示意Fig.1 Schematic diagram of the working chamber and ports of an asymmetric scroll compressor

如图1 所示，某变壁厚涡旋压缩机为非对称吸气设计，且为减少排气过程中的欠压缩和过压缩损失，动静涡旋齿中心为非对称修正，排气口设计为非圆形并增加若干泄压孔。此处对本文使用的涡旋压缩机内部过程模型［12］做必要的介绍，以便于后文具体分析的展开。

为了方便计算动盘在运转中对各个工作孔的遮挡造成的复杂几何变化，本文使用数值离散的方法，将构成工作腔和工作孔的封闭有向曲线离散为相应的有序轮廓点的集合，并结合布尔运算分析计算点集重构的各多边形间几何关系，由此对涡旋压缩机建立几何模型，各工作腔和有效工作孔的投影面积可以根据其轮廓点集，依Green公式数值积分得到：

对各工作腔和工作孔划分控制体积后，列出其质量守恒和能量守恒方程，使用各流道的几何参数及制冷剂物性对喷管模型进行修正得到泄漏流量［13］，制冷剂的物性通过调用CoolProp 开源软件获得［14］，使用四阶龙格库塔法求解得到的微分方程组，以此建立了热力学模型。

使用模型程序对涡旋压缩机进行几何和热力学模拟后，得到了动盘的运动以及气体压力分布随转角的变化规律，将动盘表面各微元上的气体压力积分，分别获得气体力和气体力矩，以考虑对称腔室内的非对称气体压力分布造成的附加的倾覆力矩。

同时，轴向间隙内的气体压力对轴向力及倾覆力矩同样会有一定影响，本文通过插值后数值积分的方法计算这部分气体压力及其影响。最后，在获得动盘动力特性的基础上，求解十字滑环的动力学方程［15］，得到十字滑环受力。

1.2 型线偏置对动盘动力学结果的影响

为方便叙述，对型线的偏置顺序为：先对型线旋转，随后进行平移。在直角坐标系下，围绕原点O 逆时针旋转角度φ0的图形，其上任意向量a 在旋转后的坐标向量ar可以通过变换矩阵B 求得：

由此可知，在给定曲轴转角时，旋转后型线上啮合点的相对位置也将改变，也即是吸气完成压缩开始的曲轴转角产生-φ0角度的平移。同时，由变换矩阵计算旋转后气体力的单位方向向量nr，得到型线旋转偏置后气体力向量fr及其气体力作用点位置向量rr如下：

将旋转后的向量代入式（2），得到旋转后的力矩Mr：

对于发生了整体平移的气体力，结合变换矩阵B 的性质化简，得到下式：

由上述分析可知，旋转仅仅改变曲轴转角对应的压缩角，不会影响到轮廓点距原点的距离，也不会影响横向气体力和轴向力及其力矩，当仅有一个背压腔且背压力均匀时，对背压力矩也无影响。

随后，将型线在XOY 平面上以向量r0平移距离（x0，y0，0），得到旋转平移偏置后的向量为：

由式（2）可知，平移对方向向量及任意力frt的大小均无影响，仅改变部分力的作用点位置，则平移后的力矩如下：

对于涡旋体侧壁微元上的横向气体压力，作用点在XOY 平面整体平移，造成了自转力矩的改变，将上式化简可得：

可知，对于横向气体力，r0×fr项仅会附加自转力矩，而对倾覆力矩无影响。

如图2 所示，动盘上表面外沿间隙内气体压力在背压和工作腔的压力之间，而背面受到了引出的中间背压和密封环内侧的排气压力。在动盘外径和背压不变的情况下，动盘背压力作用位置不发生改变，不会造成任何附加力矩。对于动盘上表面的轴向力，工作腔相对动盘中心位置的改变，仅造成了工作腔影响范围内的部分动盘轴向压力作用点的平移。这部分轴向气体力对自转力矩无影响，对倾覆力矩的影响需要通过式（9）积分求得。

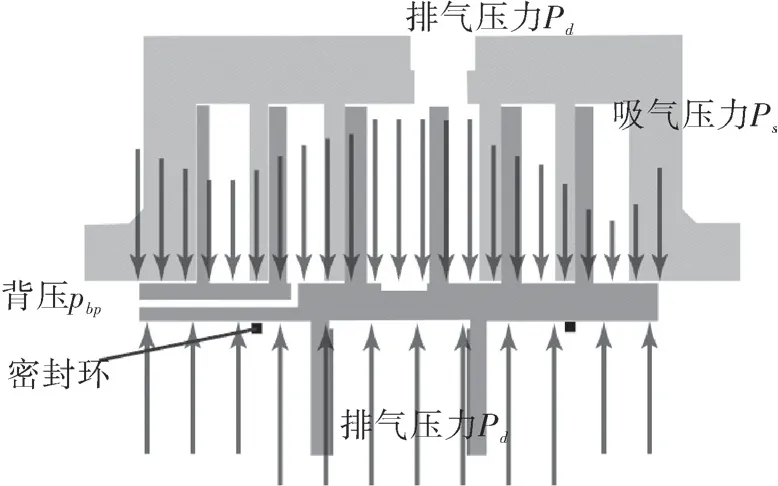
图2 动盘上下表面所受轴向气体压力分布示意Fig.2 Schematic diagram of the axial gas pressure distribution on surface of orbiting scroll

对于本文分析的静涡盘的工作腔轮廓，取离散轮廓点集上相对原点距离最大值为Rmax，再考虑到动盘回转半径以及吸气腔与背压腔之间的密封，在Rmax的基础上适当扩大，作为该平移偏置下动盘底板半径。

2 模型验证与结果分析

分析的涡旋压缩机基本几何参数和运行工况见表1，使用的制冷剂为R410A。

表1 涡旋压缩机参数及运行工况Fig.1 Parameters and operating conditions of scroll compressor

表2 模拟和试验测量背压和流量对比Tab.2 Comparison of simulated and experimentally measured backpressure and flowrate

2.1 模型验证

由于直接测量动盘受力比较困难，本文通过测量压缩机容积效率和动盘所受背压对于构建的模型进行了试验验证［12］。可以看出，在测试工况的3 个转速工况中，模拟和试验测量得到的背压的绝对误差在0.01 MPa 以内，流量的绝对误差在0.003 kg/s 以内，这验证了本文建立模型计算结果的准确性。其中，背压随着转速上升而下降，这是因为背压孔对应的工作腔压力受泄漏影响，而转速上升后，泄漏量减少使得工作腔压力下降。

2.2 动盘半径和自转力矩随偏置的变化

由上文分析可知，型线旋转对涡旋盘半径无影响，此处只对型线及工作腔平移的相关结果进行分析。距原点最远的静盘工作腔轮廓点半径Rmax随偏置向量（x0，y0）的变化曲面如图3 所示。

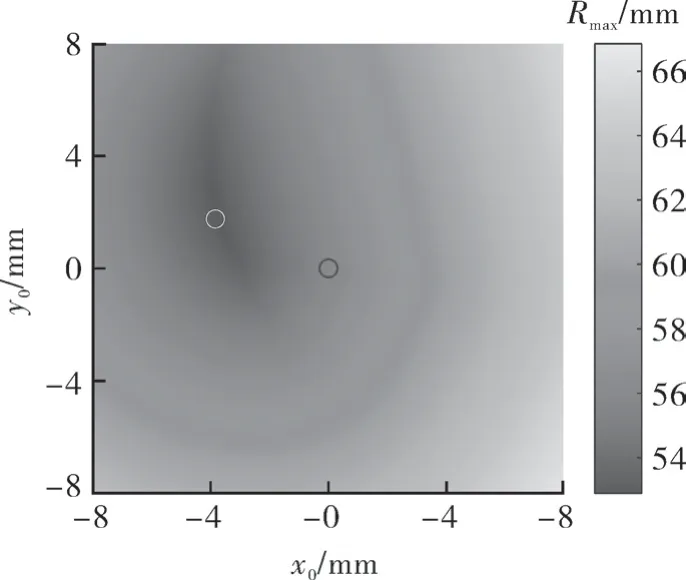
图3 静盘轮廓最大半径随平移偏置的响应曲面Fig.3 Response surface of maximum radius of stationary scroll outline with respect to various offsetting

由图可知，对于减小动盘型线半径，平移偏置存在最优值。原型线的Rmax为56.23 mm，随着x0减小和y0增加，Rmax的值也在逐渐减小，最低点出现在平移向量rRmin为（-3.84，1.76）处，此时Rmax减小到了52.88 mm，相对于原型线减少了约6.0%。需要指出的是，此时平移的方向向量并不与原轮廓的最大半径点的位置向量（55.26，10.44）平行。另外，由图可知在rRmin附近的曲面呈V 型，在曲面的谷底曲线上Rmax对平移向量并不十分敏感。

平移偏置对一周内自转力矩的最大值Ms，max和最小值Ms，min的影响曲面如图4 所示。

图4 动盘气体自转力矩最大值和最小值随平移偏置的响应曲面Fig.4 Response surface of maximum and minimum self-rotation moment to various offsetting

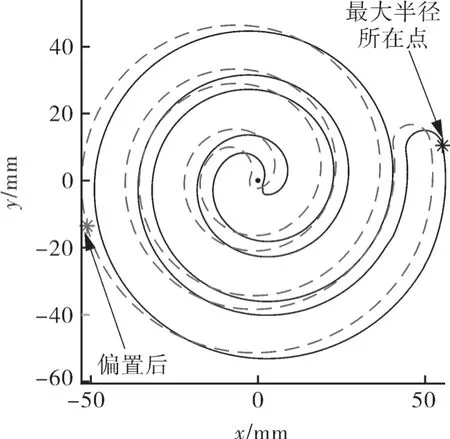
图5 原型线与偏置rRmin 后静盘最大半径轮廓点对比Fig.5 Comparison of the outline point with maximum radius of stationary scroll with and without offsetting

由于非对称吸排气设计，原型线的自转力矩在7.87～-6.59 N·m 波动，即动盘自转趋势出现了正负交替的变化。而随着向rRmin方向平移距离增加，波动的幅值开始增加，当平移rRmin使得最大外缘点半径达到最小值时，自转力矩幅值升高到了49.17 N·m。另外，当平移向量在rRmin的反方向rMmin=（1.44，-0.80）时，自转力矩的幅值最小，降低到了4.28 N·m，此时反自转力矩仍然存在，为-0.61 N·m，但此时Rmax也增加到了57.68 mm。

由rRmin和rMmin向量的方向及各曲面的形状可知，对于本文分析的涡旋压缩机来说：通过型线平移来减小动盘半径时，将会使得自转力矩幅值增加；而以减小自转力矩幅值为目的优化平移向量时，动盘底板所需的半径将会增加；无论如何调整平移向量，一周内总会出现负的自转力矩。

2.3 最小动盘半径时的几何和动力特性

以静盘中心为原点作图，平移偏置rRmin前、后的静盘工作腔轮廓分别如图5中实线和虚线所示。可以看到，原最大半径所在点在第一象限的吸气腔外缘，而通过平移偏置，该点移动到了第三象限的静涡盘内壁面型线上。

取最大半径向外增加10 mm，以0.5 为步长约取动盘底板半径，重新进行模拟计算。设动盘密度为7 850 kg/m3，计算动盘涡旋齿、底板及轴承座等结构重量后，得到的动盘各参数见表3。可以看到，使用平移偏置后，动盘半径减小了3.5 mm，总质量降低了约6.1%。实际设计时，静盘和壳体半径相应从84，88 mm 减少到80.5，84.5 mm。由此可见，型线偏置有益于减小涡旋压缩机尺寸、节省材料。

表3 偏置前后动盘参数对比Tab.3 Comparison of parameters of orbiting scroll before and after offsetting

两种情况下的动盘自转力矩随曲轴转角变化曲线如图6 所示。原型线时，动盘在100 °～ 320 °左右自转力矩为正，其余转角为负，自转力矩在一周内的平均值为1.26 N·m。当平移偏置后，正自转力矩的曲轴转角度数减小到约120 °～ 310 °，反自转的曲轴转角范围扩大，同时自转力矩在一周内的平均值略微降低至0.70 N·m。

图6 原型线与偏置rRmin 后自转力矩曲线对比Fig.6 Comparison of self-rotation moment of orbiting scroll with and without offsetting

两种情况下的十字滑环受力随曲轴转角变化曲线如图7 所示。

图7 原型线与偏置rRmin 后十字滑环受力对比Fig.7 Comparison of forces on Oldham's ring with and without offsetting

图8 原型线与偏置rRmin 且动盘半径减小后轴向力对比Fig.8 Comparison of forces on Oldham's ring of prototype and with offsetting and reduction of orbiting scroll radius

由于自转力矩都出现正负交替变化，因此，十字滑环受力同样有正负变化。受力大小的变化趋势由自转力矩大小决定，原型线时的十字滑环最大受力约78 N，而平移偏置rRmin后，最大受力是原型线的3 倍多，大幅增加到约240 N。型线偏置后，由于动盘和壳体尺寸减小的限制，十字滑环外径需要缩小，而此时十字滑环受力增加。因此可能需要通过减少十字滑环内径或增加十字滑环和滑块的高度，以保证其整体的强度以及侧面的润滑。

由于动盘直径减小，轴向压力和背压作用面积均同时减小，此时轴向力和背压力都小于原型线。但是，由于缩小盘径对应的面积上的背压要高于动盘上表面推力轴承面上处于背压与吸气压力的中间压力。因此在偏置并降低动盘外径后，推力轴承一周内的平均推力约为6 060 N，下降了5.4%。对这种情况下的动盘稳定性进行分析，由图9 可知，虽然动盘倾覆力矩变化不大，但是外径和推力的减小会使得动盘稳定系数减小。此时可能需要通过调整背压孔位置来提高背压，防止动盘倾覆，轴向间隙扩大［15-18］。

图9 原型线与偏置rRmin 且动盘半径减小后倾覆力矩变化曲线Fig.9 Variation of overturning moment on orbiting scroll of the prototype and with offsetting and reduction of orbiting scroll radius

3 结论

（1）对于不对称吸排气的涡旋压缩机来说，不论是否采取平移偏置，其自转力矩总是出现正负交替的变化，即十字滑环滑块在一周内会受到交变应力。

（2）采取合适的平移偏置能减小动盘、静盘和壳体的尺寸。以最小动盘半径为目标进行型线偏置时，动盘半径减小了3.5 mm，总质量降低了约6.1%。

（3）采取平移偏置使得动盘尺寸最小后，将会大幅度增加动盘所受的自转力矩和十字滑环交变应力的幅值。十字滑环最大受力增加到约240 N，最大受力是非偏置型线的3 倍，此时需要对十字滑环的内径或高度进行调整，以保证其强度和润滑。

（4）采取平移偏置使得动盘尺寸最小后，动盘上的各轴向气体力均会下降，其中推力轴承为6 060 N，下降了5.4%，而倾覆力矩变化幅度不大，此时需要注意调整背压以防动盘出现倾覆。