基于ANSYS 的水电站厂房刚度中心数值分析

赵廷红，陈 健

（兰州理工大学能源与动力工程学院，甘肃 兰州 730050）

0 引 言

在结构动力分析的过程中，刚度中心是一项极为重要的参数，大量研究表明［1，2］它与质量中心的相对位置决定了结构在地震等动力作用下发生平扭耦联等不良现象的剧烈程度，随着二者偏心距离的增大，结构的动位移与动应力也随之增大，控制偏心距可有效避免结构在地震作用下因扭转响应过大而发生扭转破坏。对此，我国相关规范［3］也对结构的刚度分布进行了一定的约束，从而保证结构在设计层面的合理性，同时防止因建筑物的刚度中心与质量中心之间的距离过大而出现的动力响应异常增大、乃至危及结构体系安全的问题。

对于单一单层建筑结构，通常直接采用静力学法来求解其刚度中心，即先分析整体结构的刚度分布情况，而后直接应用静力学公式求解出该结构抗侧反力的合力点［4］，即得出其刚度中心。该方法也可用于求解大型多层复杂结构刚度中心的计算，但其求解过程将非常复杂，而且也很难得到理想的结果。为了克服这种现象，研究者［5，6］提出了一些求解多层复杂结构刚度中心的方法，这些方法虽然各有特色，但它们的主要思路都是：当整体结构只在某层刚度中心作用水平力时，该层结构只有平动而不发生扭转，而其他层可以有扭转和平动，而后通过观测结构各部分在荷载作用下的响应去求解刚度中心。按照该思路，该层的刚度中心既反映了本层构件的刚度分布又反映了整体结构中其他各层构件的刚度分布情况。

目前，水电站厂房抗震研究已有大量成果并逐渐聚焦于流固耦合模拟以及非线性分析等方面，但从整体来看，其地震响应研究是滞后的［7］，关于水电站厂房平扭耦联效应的分析以及相应的刚度中心计算求解尚未获得关注。随着计算机技术的飞速发展，结构仿真模拟软件也应运而生，结合有限元技术，研究人员可以非常方便地通过数值计算近似地得到结构的刚度中心，但现阶段具备刚度中心自动求解功能的工程软件局限性太大，不适用于除土木工程外其他行业的应用，无法很好利用有限元方法的优势。水电站厂房与土木工程中的框架结构类似，但因其内部设有廊道、流道、孔洞等功能区域，而这些因素使得它的几何外形较土木工程中的框架结构体系要复杂得多，若将其内部的各部分构件按梁、板、柱等形状规则的构件进行简化再用土木行业的数值模拟软件去求解刚度中心，必然使得数值计算的准确性大打折扣，基于此，有必要将刚度中心的求解方法进行扩展。

ANSYS 是目前应用最为广泛的一款有限元分析软件，可以发挥出有限元方法最大的优势，任意形状的结构均可在精确三维建模后，通过增大结构的离散程度获取可接受的数值结果。本文拟应用ANSYS 软件结合现有求解土木工程结构刚度中心的方法来求解水电站厂房的刚度中心；此外，因考虑到有限元网格的划分是影响数值计算结果精度的主要因素之一，本文拟将研究网格的划分对刚度中心计算精度的影响，以期能为水工结构求解刚度中心时提供参考。

1 刚度中心的计算原理

1.1 基本假设

在求解建筑结构的刚度中心时，必须遵循两条基本假设［8］：①假定楼板在平面内为无限刚性，即受到平面内作用力时仅有刚体位移产生而无弹性变形；②刚性楼板上存在这样一个点，当平面内作用力的合力通过此点时，楼板只有平动位移而不发生扭转位移，否则反之。

1.2 理论公式

根据相关文献［6］，基于结构整体各层相互影响下刚度中心求解方法的理论推导过程如下：如图1，设某层刚度中心的坐标值为R（xr，yr），在质心或任意非刚度中心点O（x，y）处施加平行于x轴方向的单位力（无量纲数1），记为fx，则刚度中心R（xr，yr）处将随之产生抗侧合力，记为p，则fx与p二者同时形成一组力偶mx，楼板会由此产生扭转位移δx，若在P（x，y）处作用反向力偶mz，则楼板由此所产生扭转位移与δx方向相反，二者可相互抵消，当mz=mx时，该层楼板的扭转位移归零。

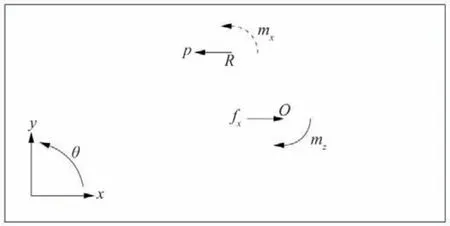
图1 计算原理Fig.1 Theory of calculation

基于上述思路，以O（x，y）为原点，列出结构由x、y及θ三个方向为分量且以柔度矩阵（即刚度矩阵的逆矩阵）表示的受力平衡方程，如下式（扭转位移与力矩以逆时针为正）：

也即：

其中，［δ］为结构的柔度矩阵，δ11至δ33为对应单位荷载作用下相应的位移，即柔度系数。

由前述有：

求解θ=0，可得下式（力偶与扭转位移以逆时针为正）：

此时注意到：δ31=δx，即上述推导中施加单位力后楼板的扭转位移；而δ33为单位扭矩作用下楼板的扭转位移，记为δz。所以有：

上式中仅有刚度中心的坐标值yr未知，故可求得。同理，可求得刚度中心的另一个坐标值xr。经整理，考虑结构整体各层相互影响时刚度中心的求解公式如下：

由于在ANSYS中无法添加单位荷载，所以柔度系数并不能够直接从柔度矩阵中获取，而且对于节点数量庞大的有限元模型而言，直接分析其刚度矩阵的组成也是不现实的。根据柔度系数的定义，δx、δy与δz的值可由点O处作用实际的荷载Fx、Fy及Mz后产生实际扭转位移θx、θy及θz求解其比值获得，所以可将计算公式可变换为：

式中：xir、yir为第i层楼板刚度中心的坐标值；xi、yi为第i层楼板荷载作用点的坐标值；θix为第i层楼板荷载作用点沿x轴正方向施加作用力时楼板的扭转位移；θiy为在第i层楼板荷载作用点沿y轴正方向施加作用力时楼板的扭转位移；θiz为第i层楼板荷载作用点沿逆时针方向施加力矩时楼板的扭转位移；Miz为在第i层楼板荷载作用点沿逆时针方向作用的力矩；Fix为第i层楼板荷载作用点沿x正方向作用的水平力；Fiy为第i层楼板荷载作用点沿y正方向作用的水平力。

1.3 刚性楼板的处理

在数值计算中，不同构件之间刚度差异太大将使得计算结果误差异常增大，甚至引起求解无法收敛的情况［9］。利用公式（8）、（9）求解结构刚度中心需要将楼板视为刚体，而建筑结构的其余部分皆为柔性体，为克服上述困难，在计算时采用ANSYS中的刚柔耦合仿真分析方法来进行处理，即通过接触算法将刚体与柔性体接触面上的节点进行耦合，从而将二者连接在一起，该方法广泛应用于机械制造、轨道交通等研究领域，是多体系统动力学与有限元分析方法相结合的表现［10］。结构刚度中心其实就是约束刚性楼板位移的柔性体所产生抗侧反力的合力点，所以在刚柔耦合分析过程中并不需要进行瞬态动力学分析，这类问题只进行静力学分析便能满足要求［11］。

在几何建模阶段将楼板单独剖分出来进行建模，计算时将其刚度行为设置为刚性，则内部程序将会在楼板的质心处创建一个包含其整体质量、质心坐标值以及转动惯量等动力特性的质量单元，并作为导向节点来表达楼板的刚体运动，故而不必再划分应力应变的网格。但为了让楼板在后处理中也能显示出来，通过设置让程序划分出表示楼板几何形状的网格。刚体与柔性体（楼板与结构主体）之间必须设置接触来进行连接，二者不能合并在一个整体（part）内，而剩余的柔性体（结构主体与地基）将合并为一个整体，使所有柔性体连续、共用节点。

由于本研究并不需要进行碰撞、摩擦等高度非线性的接触分析，楼板与结构主体在分析过程中始终保持紧密连接，所以将刚体与柔性体的接触类型设置为绑定连接。刚体与柔性体的接触算法采用多点约束法，该方法是ANSYS众多连接方法中适用性较为广泛、计算精度较高的一种方法，多点约束算法不仅适用于刚柔耦合分析，也可以将不同自由度的单元通过自动创建约束方程联系起来，所以用多点约束法对水电站厂房这类复杂建筑结构进行模拟前处理，将会大大减小数值模拟前处理的工作量［12］。多点约束法的本质是通过一个或多个节点的自由度为标准值，令其余节点的自由度与之通过数学方程建立耦合关系［12，13］，如式（10）所示，使用该方法将楼板处理为刚体后如图2所示。

图2 基于多点约束法的刚性楼板Fig.2 Rigid floor based on multi-point constraint method

式中：j为主节点的节点编号；i为从节点的节点编号；U为自由度，如位移、温度等，在本文中为位移值；Ci为加权系数；C0为常数项。

2 工程实例

2.1 工程概况

某水电站是河段上游开发规划中的第六个梯级电站，该水电站以发电为主，同时兼顾防洪、航运等功能。工程规模等级为Ⅱ等大（2）级，按百年一遇的洪水进行设计，千年一遇的洪水进行校核，对应的洪峰流量为30 000和38 100 m3/s，坝址处的多年平均流量732 m3/s，正常蓄水位对应的水库库容为1.72 亿m3。厂内溢流式水电站厂房与混凝土重力坝在结构形式、应力应变行为等方面十分相近［14］，后文以坝体、坝段进行表述。

从右岸至左岸分别为右副坝、航运坝段、泄洪闸坝段、电站厂房坝段、安装间坝段以及左副坝。其中，电站厂房坝段每两个发电机组由两侧的横缝分割为一个机组坝段，每个机组坝段的坝体下部是发电机组的过流通道，坝体上部是表孔溢洪通道，发电机组与表孔泄洪的流道交叠布置，水电站厂房在正常工作阶段有蓄水功能，当洪水来临时启用表孔进行泄洪，过流形式为厂内溢流式，结构体系的质量与刚度分布错综复杂。

2.2 坐标系设定

ANSYS 中的坐标系遵循右手定则，全局坐标系原点位于坝体上游迎水面与地基以及左岸相交处，左岸至右岸的垂直方向为x轴正方向、上游至下游的垂直方向为z轴正方向。在全局坐标系中，整体模型x方向宽35 m、y方向高225 m、z方向长369 m；坝体x方向宽35 m、y方向高75 m、z方向总长71.3 m。为便于求解刚度中心，特建立如图3所示的局部坐标系，其原点位于全局坐标系的（35，70，-4.5）处，右岸至左岸的垂直方向平行于x轴正方向、上游至下游的垂直方向平行于y轴正方向。本文以下所有计算及分析过程均基于该局部坐标系。

图3 坐标系设定Fig.3 Coordinate setting

2.3 计算模型

在以往与本文研究对象相似的动静力研究中［15，16］，取典型坝段进行分析是普遍做法，本文基于这种常规的处理方法去求解结构的刚度中心。以一段坝段为研究对象，将坝体顶部的楼板按第一节的方法设置为刚性，采用无质量地基法来考虑结构和坝基的相互作用，坝基沿上、下游及深度方向延伸1.5 至2 倍坝高，坝体结构密度为2.5×103kg/m3、弹性模量为2.8×1010Pa、泊松比为0.167；坝基的弹性模量为3×109Pa、泊松比为0.3。坝基底部为全约束，坝基四周为法相约束，由于坝段两侧由横缝分割，本文视坝段间无相互作用，各个坝段独立承受荷载作用［15］，坝体两侧视为自由面。需要注意坝基的属性尺寸、边界条件的设定等各方面因素均对结构刚度中心的求解结果产生影响。

有限元网格的类型对计算结果的精度有所影响，为得到质量较好的有限元网格，将几何模型切分为各个可以扫掠的体，划分为八节点六面体以及六节点五面体的网格单元。远离坝体一定范围外的坝基应力应变程度很小，将此部分网格尺寸增大以减轻计算成本。

在实际工程中，对于同一结构体系，数值计算往往需要划分不同的网格方案以获得具有相当精度的计算结果，而在网格整体加密的过程中，结构的应力应变将逐步收敛于真实值，即结构的刚度（柔度）发生了变化，所以刚度中心的坐标值也将随之改变，为分析刚度中心的求解在网格加密过程中的变化，对有限元模型进行整体加密，改变网格尺寸大小以及扫掠路径的单次长短，使坝体与坝基同步加密。本文共设置五组不同的网格方案进行对比分析，各方案的网格参数如表1所示，因篇幅所限，在此只列出方案3的网格划分图（图4）。

表1 网格参数Tab.1 Mesh parameter

表2 各组荷载作用下方案3的结构扭转位移Tab.2 The structural torsional displacement of scheme 3 under each group of loads

图4 有限元模型Fig.4 Finite element model

2.4 刚度中心的求解及验证

因篇幅所限，在此仅以方案3 为例叙述刚度中心的求解以及验证过程。将荷载作用点设为（35，0，0），作用平行于x轴的作用力Fx=1 N、平行于y轴的作用力Fy=1 N、绕z 轴的力矩Mz=1 N·m，边界条件的设定与荷载的施加如图5所示。

图5 边界条件及荷载施加Fig.5 Boundary conditions and load application

结构变形如图6，在Fx作用下结构发生明显的不均匀位移变形，结构整体向x轴正方向弯曲，受荷载直接作用的上游侧总体位移量比下游侧大，约为1.5 至1.8 倍，扭转位移强烈；在Fy作用下结构的变形位移规律与Fx作用时基本一致，结构整体向y轴正方向弯曲，受荷载直接作用的左岸侧的总体位移量比右岸侧大，约为1.3至1.5倍，扭转位移明显；在Mz作用下结构变形以绕z轴的扭转变形为主，从结构中心部位至最外围的位移变形逐渐增大，坝体沿河流方向三面墙的变形位移程度并无太大差异。结构在各荷载作用下的θx、θy及θz为1.995 6×10-12rad、8.209 8×10-13rad、4.6971×10-14rad。

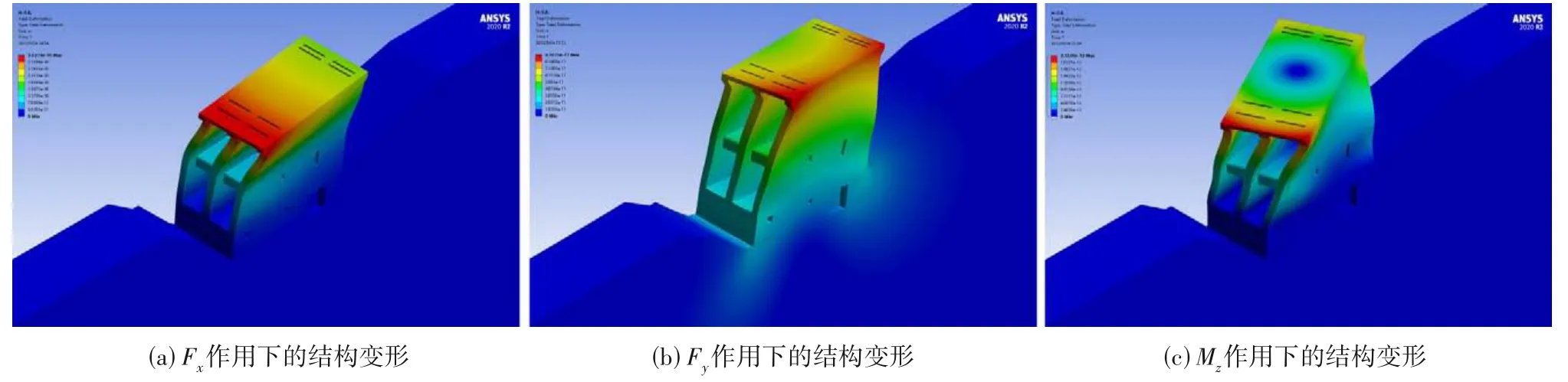
图6 结构变形Fig.6 Structural deformation

根据计算得出的扭转位移数值，结合刚度中心求解公式（8）、（9），可得出方案3 刚度中心的x和y坐标值分别为17.522 503 4与42.452 870 24。将上述过程中荷载的量级放大，令Fx=1 N、Fy=1 N 及Mz=1 N·m 为a 组，Fx=100 N、Fy=100 N 及Mz=100 N·m 为b 组，Fx=100 00 N、Fy=100 00 N 及Mz=100 00 N·m为c 组，各组荷载作用下方案3 的扭转位移以及对应的刚度中心如表3所示，可以看出，荷载大小与结构的响应呈严格线性关系，每组刚度中心的坐标值恒定不变，结合刚度中心计算公式的推导过程可知，当支撑楼板的结构处于线弹性阶段时，柔度系数的值不会随着荷载大小发生而改变，所以yir与xir为确定值，这种情况可以解释为结构刚度中心的位置保持不变，其位置只与结构本身的刚度（柔度）分布有关。

表3 各方案的结构扭转位移Tab.3 Structural torsional displacement of each scheme

按照刚度中心的定义，若在求解得出的刚度中心上施加水平力，结构应再无扭转位移产生，但由于数值计算存在误差，仍需通过结构的响应来验证其精确性，故在所求解得出的刚度中心上施加平行于x与y轴的作用力来进行验证，记为Fxr与Fyr。在ANSYS中施加荷载需要具体的几何元素或网格节点，而在求解得出的刚度中心处没有相应的加载点。考虑到楼板为刚体，根据力的平移定理，在刚度中心（17.522 503 4，42.452 870 24，0）处施加的作用力完全可以沿其作用方向等效地平移至刚性楼板的外部面上，故在（0，42.452 870 24，0）处施加平行于x轴的作用力Fxr=1 N、在（17.522 503 4，0，0）处施加平行于y轴的作用力Fyr=1 N，如图7。

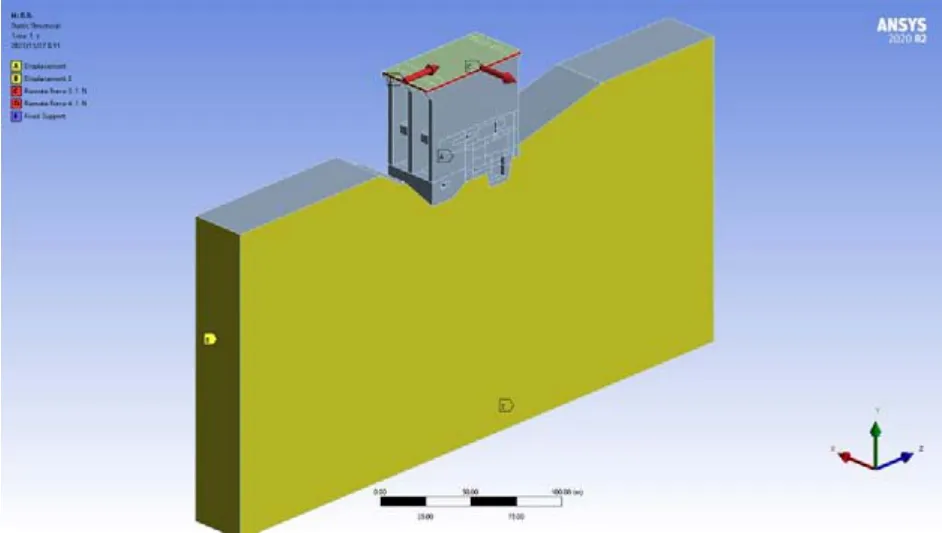
图7 精确性验证中的荷载施加Fig.7 Load application in accuracy verification

施加作用后对应的结构变形如图8 所示。由图8 可以看出，在Fxr作用下结构位移变形均匀，结构整体向x轴正方向弯曲，扭转位移难以直接观测；在Fyr作用下结构的位移变形与Fxr作用时的规律基本一致，结构整体向y轴正方向弯曲，结构无明显扭转位移产生。楼板在Fxr、Fyr作用下对应的扭转位移θxr、θyr分别为-2.927 7×10-17rad、8.870 2×10-19rad。分别对比Fx与Fxr、Fx与Fyr作用下结构的位移变形可知，当荷载作用在求解得出的刚度中心时，楼板的扭转位移明显减弱。

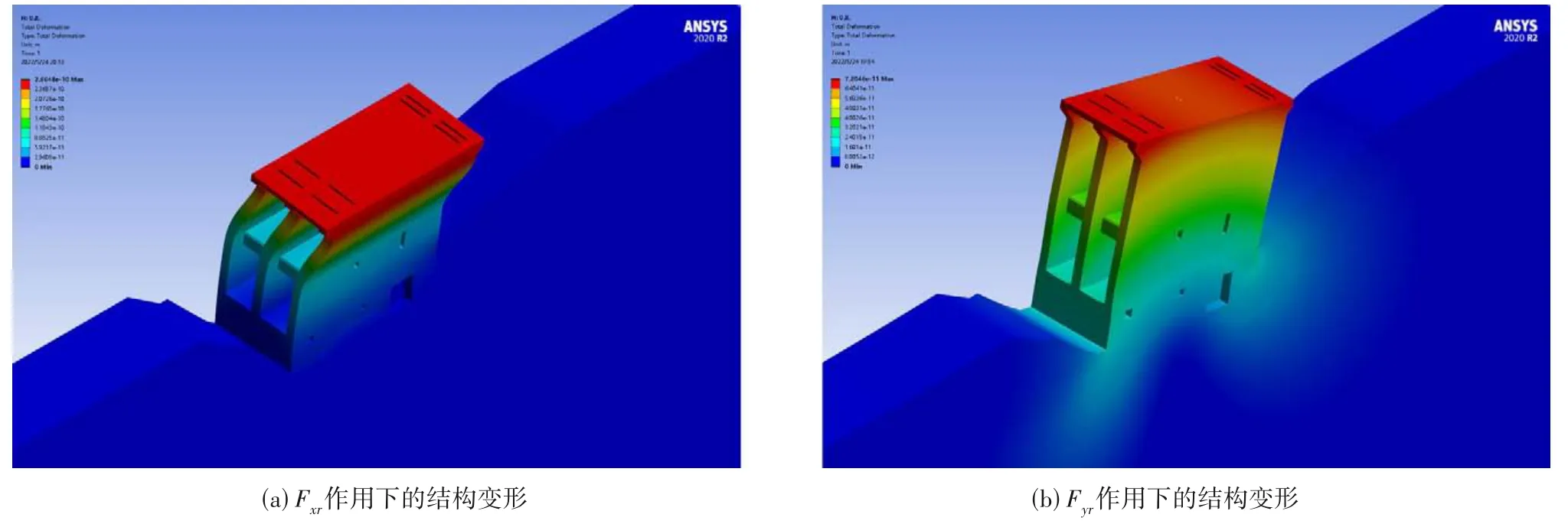
图8 精确性验证中的结构变形Fig.8 Structural deformation in accuracy verification

以在方案3 结构的刚度中心上施加荷载前后的响应为例，若求解的刚度中心准确无误，则在刚度中心上施加作用力时应无扭转产生，但实际上仍然有-2.927 7×10-17rad 的扭转位移残余，但θxr十分微小，Δxr=|-2.927 7×10-17|/1.995 6×10-12×100%≈0.001 467 078%，同理，Δyr约为0.000 108 044%，误差在0.005%以下，认为求解得出的刚度中心满足要求。

运用有限元方法进行数值计算的特点是数值结果会随着结构离散化程度的增大而逐渐收敛于精确解，所以数值模拟需要进行网格无关性的验证来说明结果的准确，而刚度中心的坐标值取决于各柔度系数的比值，对扭转位移的变化比较敏感，若各方案的扭转位移在网格加密过程中变化得不一样，则各方案下计算得出的刚度中心也不尽相同。不同网格方案下计算得出的楼板扭转位移θx、θy及θz如表3 所示，其变化趋势如图9所示。

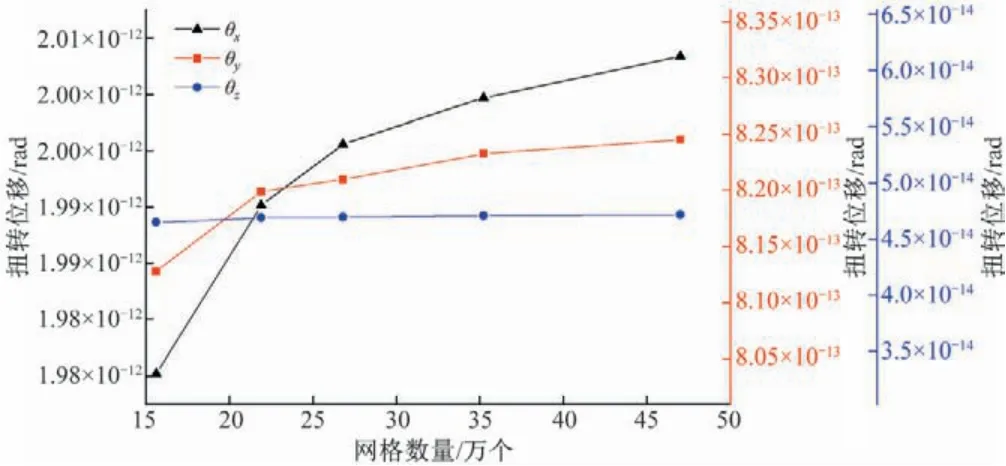
图9 网格加密对扭转位移的影响Fig.9 Influence of mesh refinement on torsional displacement

由表3 及图9 可以看出：所有方案中结构扭转位移在加密前后的误差不大于1%，可认为本次试验所有方案均已达到与网格密度无关的状态，当网格数量大约高于25 万时，结构位移变形的变化将更加平缓；各方案结构扭转位移的变化程度并不一样，3 组数据中，θx每次加密后的变化程度最大，θy次之，θz最小，所以后续以结构扭转位移计算得出各方案的刚度中心也存在着偏差。

各方案刚度中心的计算值与精确性验证如表4所示。由表可看出各方案的刚度中心坐标值在某个范围内变化，通过对比表3 与表4 的数据，这是因为网格划分发生变化时，结构的刚度（柔度）发生了不均匀的变化，使得每个方案求解得出的刚度中心总是不一样的，这也导致了θxr与θyr的值并不能严格呈现下降趋势；总体而言，在各方案刚度中心上施加荷载所引起的扭转位移甚微，Δxr与Δyr皆不大于0.005%，对实际工程而言满足精度要求。

表4 各方案的刚度中心坐标及精确性验证Tab.4 Stiffness center coordinates of each scheme and accuracy verification

2.5 关于刚度中心数值精度的讨论

在本文的有限元模型中，当作用力大小、方向均不变时，随着网格加密，扭转位移θx、θy与θz的变化是不一致的，结合理论知识，这种现象说明结构本身的刚度分布发生了变化。从x与y方向上的平动以及绕z轴的扭转这3 个自由度建立如式（11）所示的受力平衡方程［17］，由此可知结构在x、y方向平动位移值的大小以及绕z轴扭转位移值的大小最终取决于刚度矩阵中x、y方向的抗侧刚度的分布。根据有限元方法的特点，产生该现象是因为x与y方向上的网格加密不均匀导致计算模型在网格加密的过程中x与y方向上的抗侧刚度变化程度不一样的缘故。

其中：

式中：［K］为刚度矩阵；xi、yi为第i个抗侧构件以荷载作用点为原点的坐标值；∑k（ex，i）、∑k（ey，i）为结构x、y方向的抗侧刚度之和；∑k（ex，i）yi2+∑k（ey，i）xi2为结构的抗扭刚度。

以不同方案的结构在Fx及Fy作用下的响应进行说明。令该点在Fx作用下x方向的位移值为α、y方向的位移值为β，该点在Fy作用下x方向的位移值为ζ、y方向的位移值为ξ，各位移值的变化曲线按等比例绘制于图10，各方案中各位移值的具体数据如表5所示。

表5 各方案的结构位移Tab.5 Structural displacement of each scheme

图10 网格加密对结构位移的影响Fig.10 Influence of mesh refinement on structural displacement

由表5及图10可以看出：在4组结构响应曲线中，Fx作用时结构在x方向上的位移最大，Fy作用时结构在y方向上的位移次之，其余2 组的位移大小十分接近，从支撑楼板的三面墙体分析，其在y方向上的抗侧刚度远比x方向大，所以导致了α 曲线上的值比ξ 要小，计算结果符合物理规律；从4 组曲线的变化率可以看出，α 曲线远比其他3 组曲线的变化程度要大，说明在网格加密的过程中x与y方向上的离散程度变化不均匀，使得对应方向上的抗侧刚度变化不一致，最终导致刚度中心计算误差的出现。

3 结 论

（1）使用ANSYS求解刚度中心是可行且高效的，为研究人员分析计算结构的刚度中心、掌握结构动力特性提供了新的途径。

（2）由表3 及表5、图9 及图10 可知，随着网格的不断加密，结构的响应越来越趋近于真实值，但网格的加密导致计算模型在不同方向上的抗侧刚度发生不均匀变化，从而使得刚度中心的坐标值发生偏差，为减小此过程中引起的误差，网格的加密应尽量保持均匀；刚度中心验证与求解过程中的计算模型需要保证是一致的，网格划分参数不允许发生改变。

（3）对于（2）而言，在实际工程应用中，要做到整体网格完全均匀加密是不现实的。通过本试验可看出，计算模型达到网格无关性后，继续加密网格所引起的误差是可以忽略的，所以，研究者可根据实际需求，综合考虑重点关注的物理量以及刚度中心计算值的数值误差求得刚度中心。