弱混合条件下支流入汇口水力特性数值模拟

陈雪妮，杨中华，尹 炜，吴 菲，白凤朋

（1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072； 2. 长江水资源保护科学研究所，湖北 武汉 430051； 3. 长江水利委员会湖库水源地面源污染生态调控重点实验室，湖北 武汉 430051； 4. 湖北工业大学土木建筑与环境学院，湖北 武汉 430068）

0 引 言

明渠交汇现象普遍存在于天然河流系统中［1］，交汇区域水动力特性复杂多变，干流受到支流顶托作用在交汇口上游发生壅水现象、流速降低，下游靠近支流侧形成分离区，对污染物有滞留作用［2，3］；当支流来流量较小时，支流入汇口形成大面积回流区域，造成水体滞留、泥沙沉降和污染物聚集［4］。因此明渠交汇口是影响水环境保护和航运整治的关键部位，交汇区水力特性的研究一直是水利工程设计和运行管理中的重点和难点。

国内外不少学者针对干支流交汇区域水流特性及其变化规律展开了研究。Taylor［5］最早于1944 年对明渠交汇问题开展了试验研究，明确提出了交汇口研究的必要性及重要性，为后续研究建立了基础。此后，Best［6］通过水槽模型试验提出将交汇河段划分为滞留区、偏离区、分离区、加速区、剪切层和流动复原区六个区域。Yang［7］分别采用标准k-ε、RNGk-ε和RSM模型分析了不同湍流模型对分离区尺寸和二次流的影响，发现RNGk-ε模型模拟效果最好。Webber［8］等基于ADV 对90°交汇口三维水流结构进行了详细测量，为交汇口的数值模拟研究提供了大量实验数据作为验证支撑。茅泽育［9］通过模型试验和理论分析发现交汇区域断面存在二次环流，且分离区尺寸与汇流比有关。目前交汇区的研究成果多侧重于交汇角和汇流比对汇流口及干流河段的影响作用［10-12］，近年来部分学者开始将干支流交汇段的研究重心向支流河道转移，张琦［13］通过数值模拟对明渠交汇段的小型支流河道展开了研究，重点分析了不同弯曲形态和不同汇流比影响下的支流河口水面形态和泄流能力。

当支流来流量极小时，水体和污染物无法下泄进入干流河道，在适宜的光照和温度条件下易造成库区水体富营养化。近年来随着对库区支流富营养化问题研究的深入，水体流速、表层环流和紊动混合等水动力特征越来越多的成为研究富营养化问题的重要因子［14，15］。本文将这种支流入汇不影响干流流场的交汇条件定义为弱混合条件，弱混合条件下交汇河段的交汇角和汇流比对支流入汇口水力特性的影响机制尚不明晰。陆建宇［16］对河道型水库库区干支流交汇段进行概化，通过建立三维数学模型研究了天然河道尺度下不同交汇角对支流入汇口紊动能分布和床面切应力的作用机制，发现弱混合条件下紊动能峰值区域随交汇角增加逐渐向支流右岸上层移动，交汇角＜90°时紊动能变化较小，交汇角＞90°时紊动能增长幅度较大。陆对弱混合条件下交汇角对支流紊动特性的影响较为细致，而汇流比对紊动能分布的影响以及交汇角和汇流比两个因素影响的对比有待进一步研究。

基于此，本文以弱混合条件下交汇河段支流入汇口水力特性为研究对象，采用室内水槽试验数据验证后的RNGk-ε模型，对不同交汇角和不同汇流比的支流入汇口水动力特性和紊动特性进行分析和研究，以期阐明交汇角和汇流比对支流入汇口水力特性的影响。

1 数学模型

1.1 控制方程

连续性方程：

式中：ui为xi方向的时均速度；i=1，2，3。

动量方程：

式中：ρ为水的密度；p为时均压强；t为时间；γi为水的动力黏性系数；fi为外部体积力。

1.2 RNG k-ε紊流模型

RNGk-ε模型对紊动黏度进行修正，从而引入平均流动中的漩流运动状况，可以很好地反映应变率高及流线弯旋状态明显的流体形态［17］。RNGk-ε模型的k及ε方程如下：

k方程：

ε方程：

式中：αk、αε为湍流普朗特数，均取1.39；μeff=μ+μt，，Cμ= 0.084 5；为紊动能平均速度梯度产生项；Gb为浮力产生项，不可压缩流体Gb= 0；模化常数C1ε= 1.42，C2ε= 1.92，C3ε= 1.0；，η0=4.377，β= 0.012，；Sk、Sε为源项。

2 数值模型及验证

2.1 试验模型及量测系统

试验在武汉大学水力学实验室的矩形玻璃水槽中进行。干流水槽长8 m，宽0.3 m，高0.5 m，底坡为1/1 000，进口采用水泵供水并通过多道消浪栅平稳水流，在水槽上游采用三角形薄壁量水堰测量流量。支流水槽长1.8 m，宽0.1 m，高0.45 m，支流采用管道供水，进口处铺设鹅卵石平稳水流，流量控制系统采用精度为0.5 级的电磁流量计。水槽出口处设有尾门以控制水位。

流速采用粒子图像测速仪（Particle Image Velocimetry，简称PIV）进行测量，PIV 拍摄范围为18 cm×14 cm，水槽可视化测量区域共80 cm，A～D 为相机拍摄位置，x-y平面测量Y1～Y4四个断面，x-z平面测量S1～S3三个断面，相机位置和断面位置如图1所示。

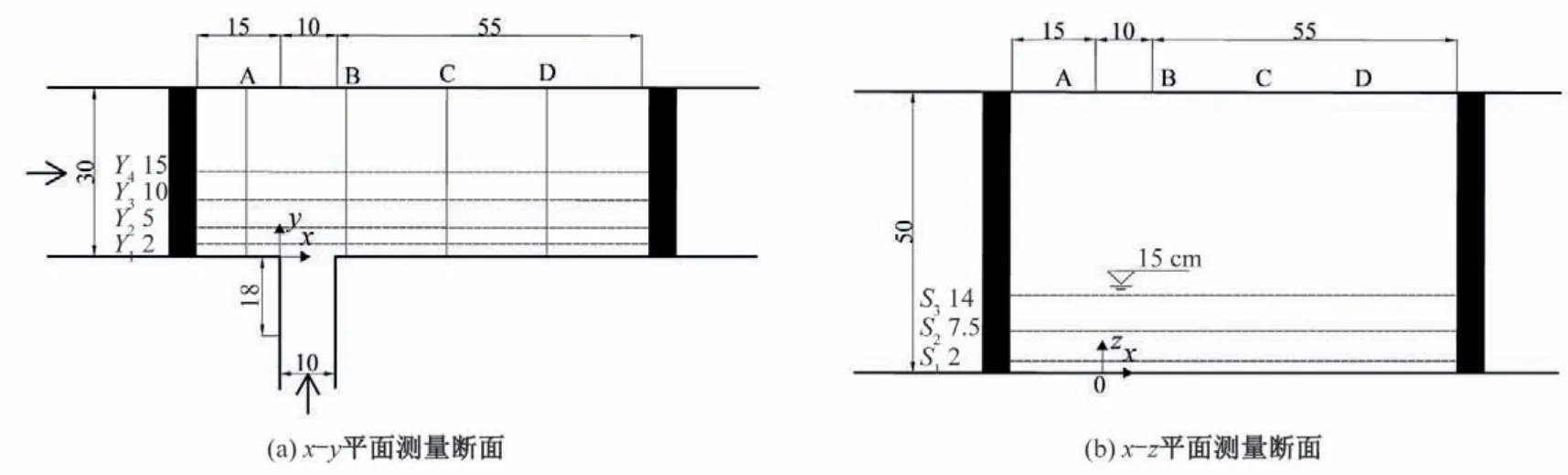
图1 水槽试验 PIV拍摄断面布置示意图（单位：cm）Fig.1 PIV shooting section layout diagram of experiment

2.2 计算区域及网格划分

图2 所示为交汇角α=90°工况的计算区域，原点位于交汇点上游，x、y、z轴正方向如图所示。根据试验水槽进行建模，干流宽0.3 m，水深h=0.15 m，支流长1.8 m，宽0.1 m，交汇口距干流入口3.2 m。选用六面体结构化网格对计算区域进行剖分（图3），网格数为345 600（α=90°）～398 340（α=150°），横向最大网格尺寸为0.01 m，纵向为0.02 m，垂向为0.01 m。对交汇口附近网格进行加密。

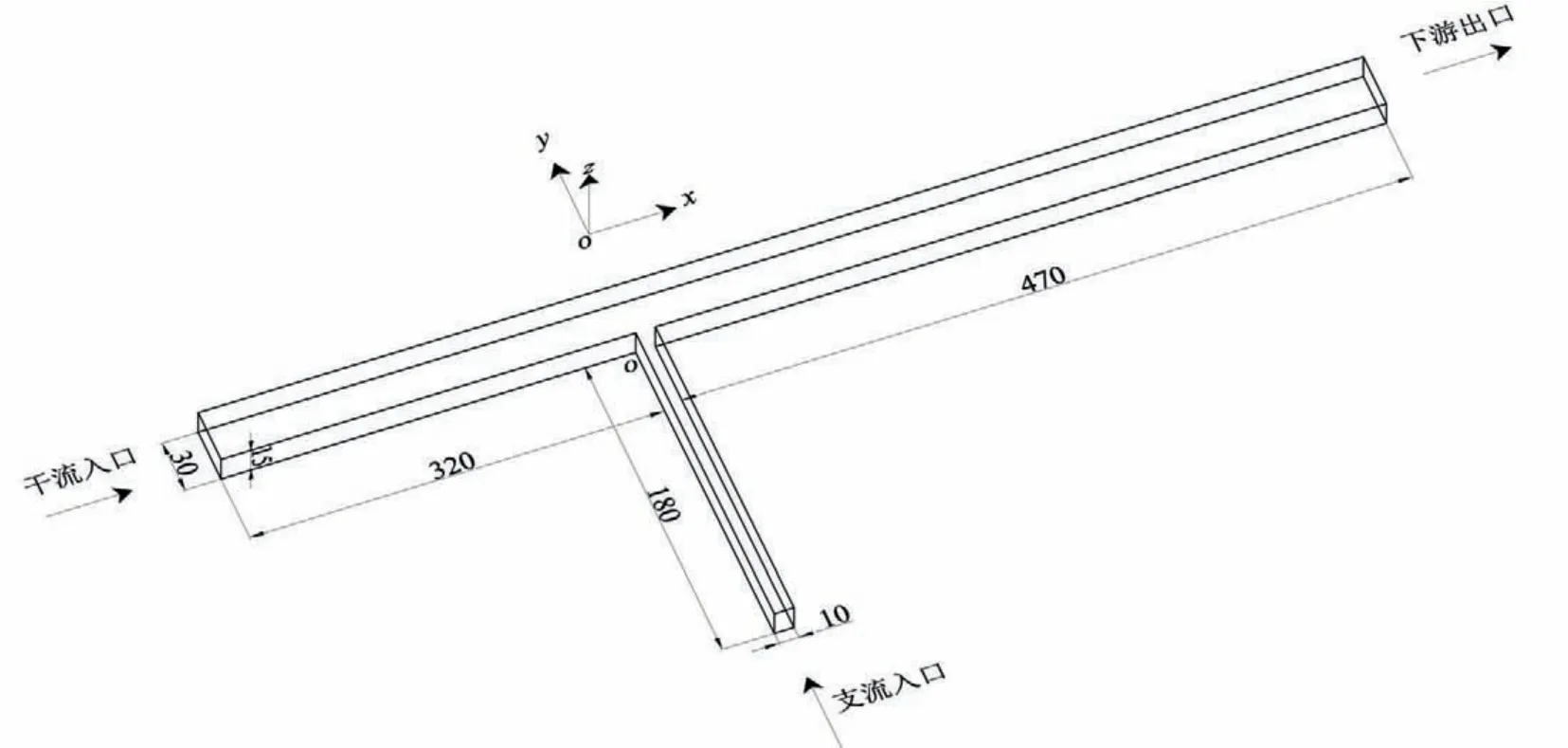
图2 计算区域示意图（单位：cm）Fig.2 Computational area

图3 计算网格示意图Fig.3 Computational mesh

2.3 数值方法、边界条件及计算工况

控制方程的离散方法采用有限体积法，速度和压力解耦采用PISO 算法［18］，其他项离散均采用QUICK 格式，以RNGk-ε模型封闭雷诺时均方程中的紊动黏性系数。干、支流进口边界采用速度进口，流向垂直于进口断面，干流入口流速Um=0.22 m/s，支流入口流速va随工况不同有所变化；出口边界条件采用压力出口，满足静压假定；进出口的紊动能和耗散率边界值均按照经验公式的计算结果初始化；计算区域底部及侧壁采用无滑移边界条件；根据水槽模型试验观察，低汇流比条件下支流水面比降较小，故模型顶部采用刚盖假定。

为了研究交汇角和汇流比对支流流场的影响，设计6 种计算工况，具体工况设置如表1所示。

表1 数值模拟计算工况Tab.1 Case setting of numerical simulation

2.4 模型验证

选取水槽模型试验工况中交汇角α=90°、汇流比RQ=0.25（干支流流量分别为Q干流=10 L/s、Q支流=2.5 L/s）的测量结果对模型结果进行验证，其中模型边界条件与相应试验边界参数一致。以支流宽度W为特征长度对横纵坐标进行无量纲化得到x*、y*，无量纲化水深z*=z/h，将时均流速U除以干流入口流速Um得到无量纲化U*，下文中出现的物理量若无特别说明均经过上述量纲归一化处理。图4 所示为交汇口附近区域近水面处（z*=0.93）的x-y平面流场矢量图与实测结果的对比结果，可以看出支流入汇后干流交汇区产生水流偏转现象，交汇区下游形成分离区，数值模拟可以较好反映出交汇口附近流速偏转情况、分离区范围及二次流现象。图5为不同位置处的无量纲化流速分量Ux、Uz沿垂向分布情况与水槽试验实测值Vx、Vz的对比结果，可以看出模拟结果与实测资料吻合较好。

图4 近水面处流场矢量图与实测结果的对比结果Fig.4 Comparison of velocity vector near the water surface with the measured results

图5 不同位置时均流速垂向分布与实测数据的对比结果Fig.5 Comparison of the vertical distribution of time-averaged flow velocity at different positions with the measured results

3 支流入汇口水力特性

3.1 支流入汇口水流结构分区

当天然河道中支流来流较小时，支流水体由于干流的阻碍作用在入汇口右岸产生大范围回流，将产生回流的区域定义为回水区，回水区的存在造成水面收缩从而导致左岸水流加速形成加速区［图6（a）］。对于回水区尺寸的界定，如图6（b）所示，参考分离区尺寸界定的等值线法［8，19］，即顺支流向流速为零的等值线为回水区边界，零等值线区域的最大长度和最大宽度定义为回水区的长度L和宽度B。

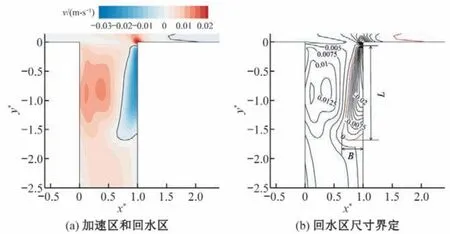
图6 支流入汇口水流结构分区Fig.6 Tributary confluence flow structure zones

3.1.1 不同水深断面支流回水区形状

交汇角α=90°、汇流比RQ=0.005 条件下回水区长度L、宽度B在不同水深断面的分布规律如图7 所示，L和B沿水深方向整体呈现出先减小后增加的变化规律。近底面附近（z*＜0.2）回水区形状为“半葫芦”型（图8），L和B为全水深断面最大值，说明近底面处入汇口回流范围较大，原因可能为此时支流流速较小（接近于0），受到干流阻碍作用后更易发生流向偏转。随着水深断面上移，L和B都逐渐减小；回水区形状和宽度在z*=0.4～0.85 范围内基本不变，表明中上层水体回水区和加速区维持动态平衡；最后在近水面处（z*＞0.85）L和B都出现较大幅度增长，回水区形状转变为“钩”型，这是由于回水区在表层位置流速较大的缘故。

图7 支流回水区形状参数沿垂线分布Fig.7 Vertical distribution of tributary backwater zone shape parameters

图8 支流回水区形状示意图Fig.8 Schematic diagram of the tributary backwater zone

3.1.2 交汇角和汇流比影响下入汇口分区特性

图9 为不同交汇条件下支流入汇口近水面处（z*=0.93）x-y平面流速云图。α=30°时，回水区范围从左岸向支流上游延伸至右岸，回流流速峰值出现在交汇口右岸处；α=90°时，右岸回水区和左岸加速区分区明显且形状规则，流速峰值较30°时有所减小；当交汇角增加至150°时，回流范围基本覆盖了整个支流入汇口，回水区长度L长达8.66W，加速区紧贴左岸呈细长三角形形状。随着支流来流量增加［图9（b）、（d）、（e）、（f）］，汇流比增大，回水区和加速区范围逐渐缩小，流速峰值也随之减小，当RQ增加至0.01 时，回水区和加速区消失，支流入汇基本不再受到干流的影响，表层水体恢复至正常流动。

图9 不同工况下入汇口x-y平面流速云图Fig.9 Flow velocity clouds under different cases in x-y plane

3.2 汇流比影响下入汇口纵向时均流速分布

图10 为α=90°时不同汇流比下不同位置处纵向时均流速沿垂线分布图（其中v/va是以支流进口流速va为基准的无量纲化纵向流速）。可以看出，4种汇流比下不同横截面处左岸流速分布基本遵循对数分布规律，且汇流比越小加速区越明显；随着x增加，支流右岸流速逐渐减小并产生回流现象。近交汇口（y*=-0.2）截面上的回流现象仅出现在近右岸壁面处。沿支流向上游至y*=-1.0 截面处，加速区内流速增加，RQ≤0.008 工况下回水区范围沿横向扩大至x*=0.8处，RQ=0.01时右岸流速分布恢复至对数分布，表明y*=-1.0 截面上水体基本不再受到干流影响。至y*=-2横截面，除RQ=0.005 时仍有小范围回流，其余工况下支流均恢复正常流动。

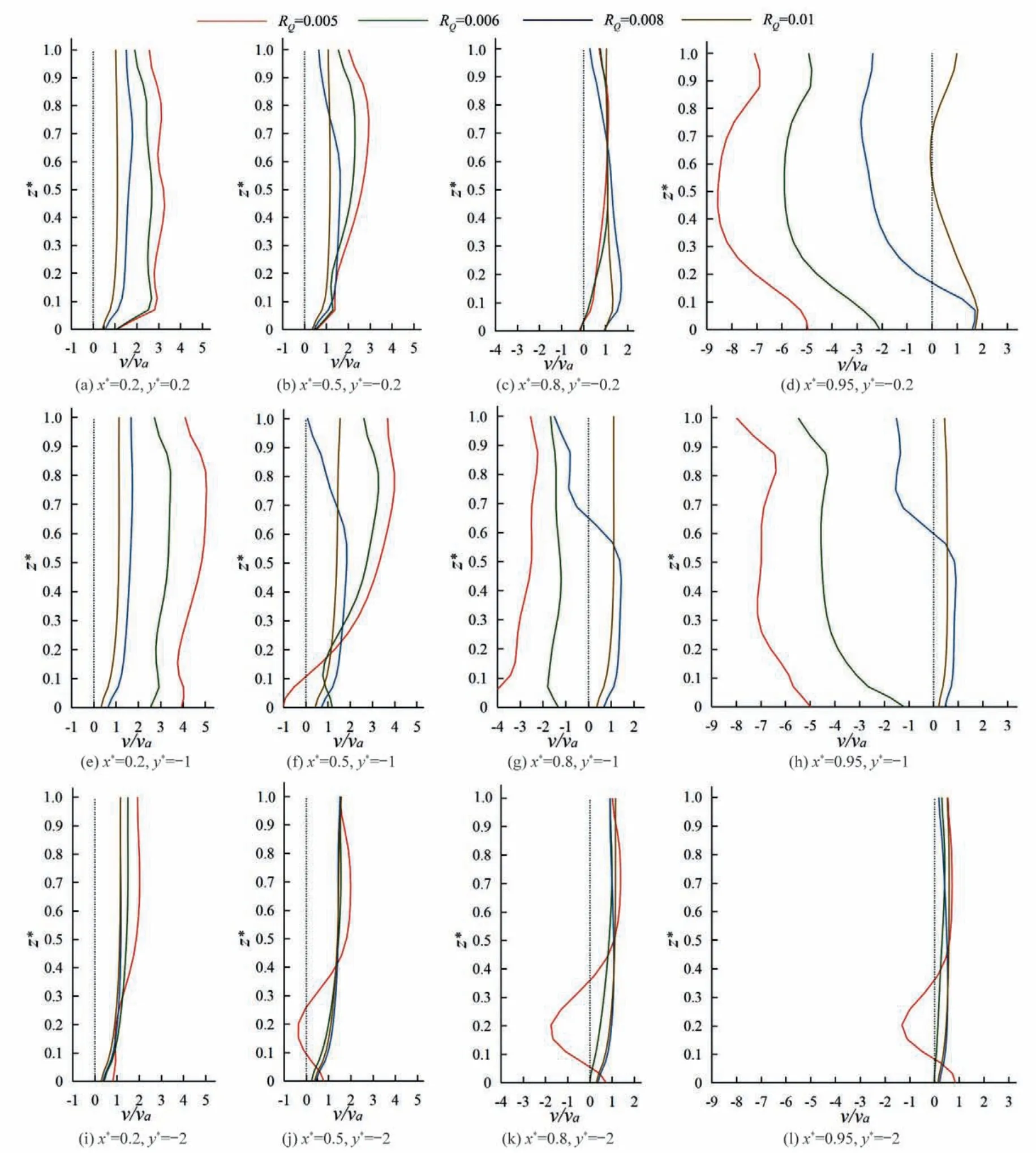
图10 不同汇流比下不同位置纵向流速沿垂线分布Fig.10 Vertical distribution of longitudinal velocity with different convergence ratios

3.3 交汇角和汇流比影响下入汇口紊动特性

水流的紊动特性是影响藻类生长的重要水动力因子，而紊动能是衡量交汇区紊动强度的重要参数，本节对弱混合条件下支流入汇口紊动能分布进行了分析研究。综合3.1 节和3.2 节可知，l*＜0.2 时入汇口分区不明显（其中l*=l/W，为支流断面至交汇口的无量纲化距离），l*＞0.2 时A5 工况下入汇口流速恢复正常，故选取断面M（l*=0.2）分析交汇口水流的紊动能分布（图11）。α=30°时，断面M右岸水面处有极小的紊动能，水流掺混均发生在l*＜0.2 近交汇口范围内。随着交汇角增加，紊动能峰值区域逐渐向支流上游移动，且峰值区域面积和峰值大小显著增大。在不同汇流比条件下，RQ=0.005 时紊动能峰值出现在断面M右侧中部，峰值大小约为3.29×10-4m2/s2，表明干支流掺混主要发生在支流右岸。随着汇流比增加，紊动能峰值区域逐渐减小且向水面移动。RQ=0.01 时，整个断面紊动能都较小，说明此时干支流掺混区域已逐渐脱离支流。

图11 不同工况下断面M紊动能分布Fig.11 Turbulent kinetic energy distribution of cross-section M under different cases

图12 为不同交汇条件下断面M纵向流速分布，正值区域（红色）表示支流水体入汇干流，负值区域（蓝色）表示水体倒灌支流。交汇角α=30°时，回流主要发生在水面处；随着交汇角增加，回流区逐渐转移至右岸全水深断面；α=150°时，回流区占据右侧大部分区域，干支流掺混最为剧烈，产生紊动能峰值区域［图11（c）］。如图所示，4种汇流比工况下均表现为左侧入汇右侧倒灌，回流流速峰值均出现在右岸壁面，表明倒灌水体从右岸进入支流后与来流水体形成掺混，导致附近流速梯度增加形成紊动能峰值区；随着汇流比增加，负值区域范围减小且逐渐上移，表明水体倒灌也随之向右岸上层发展。

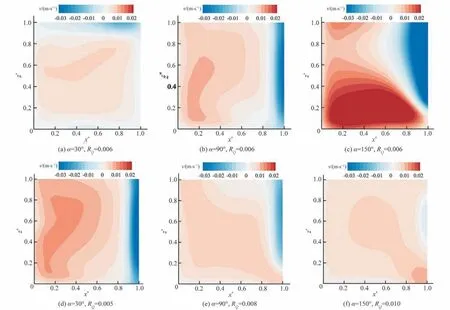
图12 不同工况下断面M的纵向流速分布Fig.12 Longitudinal velocity distribution of cross-section M under different cases

4 结 论

通过数值模拟对不同交汇角和不同汇流比下支流入汇口的回水区范围、紊动能和流速分布进行了研究，得到了低汇流比下干流对支流入汇口水流特性和紊动特性的影响随交汇角和汇流比的变化情况。

（1） 弱混合条件下支流入汇口右岸产生回流形成回水区，左侧水体挤压形成加速区。

（2） 支流回水区长度和形状变化主要受到交汇角和汇流比两种因素影响，不同交汇角条件下回水区长度大小为：150°＞30°＞90°；交汇角α=90°时回水区长度随汇流比RQ的增加而减小，RQ=0.01时回水区基本消失。

（3） 回流流速峰值出现在近右岸壁面处，汇流比RQ越小，回水区最大宽度的横截面位置距交汇口越远；交汇角α=90°时支流入汇口受影响区域在y*＞-2范围内。

（4） 在不同交汇角和汇流比条件下均存在紊动能峰值区域，区域面积及峰值大小与汇流比RQ成反比，与交汇角α成正比；交汇角对紊动能的影响较汇流比更大。