灌区新旧输水渡槽协同防洪风险分析

刘开颜，付 湘，龚来红，谢亨旺，刘双郡

（1. 武汉大学 水资源工程与调度全国重点实验室，湖北 武汉 430072；2. 武汉大学 海绵城市建设水系统科学湖北省重点实验室，湖北 武汉 430072； 3. 江西省灌溉试验中心站，江西 南昌 330201）

1 研究背景

在气候变化与人类活动影响下，洪水风险加剧，严重威胁人民群众的生命财产安全，影响了社会安定和经济的可持续发展。正确评估水利工程防洪风险，是防洪减灾领域的一项基础性工作，以期为各项防洪减灾措施制定与洪水风险管理提供重要依据。

近年来，国内外众多学者对于水利工程防洪风险进行了大量的研究，主要集中在风险评估方法及模型应用方面：PHAM等［1］开发了一个基于混合人工智能模型的洪水风险框架，将AdaBoost 算法与决策表结合，利用洪水敏感性图和洪水后果图生成洪水风险图，在缺乏时间序列气象和流量数据的情况下也可以对洪水风险进行评估；王文圣等［2］明确了次风险和年风险两种洪水风险概念，探讨以年最大洪水信息为基础的年风险度和以年内最大及次大洪水信息为基础的年风险度的差异；周方明等［3］针对水库大坝的水文、水力及工程结构等因素的不确定性，构建了时变随机变量量化的函数模型和缓变型防洪风险分析模型，定量分析大坝防洪安全；杨震宇等［4］针对三峡水库汛期中小洪水调度中的各类风险问题，分析中小洪水的特性，并建立各类风险指示函数，提出了防洪、地质、发电等多角度的中小洪水调度性能风险评估方法。FLORES 等［5］提出了一种面向对象的混合动态贝叶斯网络，得到的模型能够较为准确地预测洪水水位，由此对地中海流域洪水风险进行了评估；HOSSEINI等［6］使用GLMBoost、RF 和BayesGLM 三种最先进的机器学习模型对受洪水强烈影响的地区的山洪暴发进行建模，能够有效地预测数据稀缺地区的洪水风险；陈华等［7］利用防洪安全领域积累的监测数据，通过融合态势感知相关理论，提出面向流域防洪安全的态势图谱构建及可视化方法，并应用于丹江口库区；张丹等［8］建立了风险评估的模糊灰关联故障树模型以识别及评估水利水电工程的社会稳定风险；NACHAPPA 等［9］耦合多准则决策分析模型及机器学习模型绘制基于11 个洪水调节因素得出的洪水敏感性图，并使用Dempster Shafer理论优化，该方法在全球都具有普适性，为洪水评估和预防提供了较为准确的结果；张启义等［10］总结五类主要防洪风险事件，再利用故障树法识别各类风险事件的风险因子，在对现状条件下所有左排渡槽的防洪风险因子进行详细调查的基础上，有针对性地提出了除险及防范措施；张晓琦等［11］将经济学条件风险价值理论引入防洪评价领域，辨识各水库防洪库容值对库群系统防洪风险的影响程度及各水库间协同防洪的互馈方式。

输水渡槽作为水利工程中的重要组成部分，承担着防洪、供水、航运等多项功能，对于工程沿线的人民生活有着重大的影响，故对其防洪风险进行合理的评价研究，对于水利工程整体的防洪安全意义重大［12，13］。冯平等［14］采用二维复合事件风险组合模型，通过两两组合求解南水北调中线工程总干渠河北省段的防洪风险，但该模型只考虑了水文要素，并没有考虑工程本身的结构等特征。贾超等［15］对渡槽结构逐一进行了破坏模式的分析，建立了相应的功能函数，计算出渡槽侧板、底板、底梁等结构的可靠指标，但他只考虑了渡槽中水体对渡槽的作用，没有从水文因素的角度考虑长距离输水工程的风险。陈进［16］等采用系统和风险分析理论，从水文、建筑物、经济、政策、环境和社会等方面分析了跨流域长距离调水工程系统的风险因子及影响方式，对调水工程建设和运行过程中的各类风险进行了初步的风险评价。

水利工程正常运行多年后，由于自然或人为因素的影响导致运行条件较原设计发生变化，引发防洪安全问题，评估运行条件变化后的工程所面临的防洪风险对其安全运行管理具有重大意义。因此本文以江西省赣抚平原岗前渡槽为研究对象，综合考虑水文、工程结构等特性，依据其工程设计与运行现状整理分析新、旧岗前渡槽的特征控制水位。针对洪峰流量符合皮尔逊三型（P-Ⅲ）分布和正态分布的两种情况，依据调洪计算方法进行典型洪水过程的“峰比”放大得到洪水输入数据，以特征控制水位为约束条件，运用蒙特卡罗随机模拟方法求解新旧岗前渡槽协同防洪风险。

2 研究方法

为了定量描述渡槽承担的防洪风险，可将其定义为：在规定的时间内，天然来（洪）水超过渡槽的输水能力的概率［17，18］，若渡槽有最低安全运行水位的要求，则定义可进一步转化为：在规定时间内，渡槽内流量超过其设计流量或低于其防洪安全运行最小流量的概率，数学表达式为：

式中：RP表示发生频率为P的洪水时渡槽承担的防洪风险；Qkt表示第k个渡槽在第t时段内的流量，m³/s；Qkd表示第k个渡槽的设计洪水流量，m³/s；Qks表示第k个渡槽能维持防洪安全运行的最小流量，m³/s。

为了利用公式（1）进行风险计算，考虑Qkt的随机分布：假设天然来（洪）水最大洪峰流量概率密度分布函数f(Qm)是P-Ⅲ分布或正态分布，则任一频率P对应的洪峰流量Qm可由函数求得，再采用同倍比放大法放大典型洪水过程线，使放大后的洪峰流量等于设计洪峰流量Qm，令其出现的频率等于设计标准P，即认为所得的过程线是待求的设计洪水过程线。

若时段内天然来（洪）水最大洪峰流量概率密度分布函数f(Qm)满足P-Ⅲ分布，则表达式为［19］：

式中：α、β、a0为P-Ⅲ型分布的形状、尺度和位置参数；Γ(α)为α的伽马函数。

3个参数α、β、a0的计算方法如下：

式中：EX为总体均值；Cs为偏态系数；Cv为变差系数。

若时段内天然来（洪）水最大洪峰流量概率密度分布函数f(Qm)满足正态分布，则表达式为：

式中：σ为标准差； e为自然对数的底。

渡槽内水位和流量的对应关系可以通过明渠均匀流公式建立，当渡槽的坡度较为平缓且过水断面为矩形时，各时段流量与水位的计算公式如下：

式中：Akt表示第k个渡槽在第t时段的过水断面面积，m2；Ckt表示第k个渡槽在第t时段的谢才系数；Rkt表示第k个渡槽在第t时段的水力半径m；ik表示第k个渡槽的坡度；dk表示第k个渡槽过水断面的宽度，m；hkt表示第k个渡槽在第t时段内水平面距离槽底的高度，m。

由于公式（2）和（4）难以具体求解，故本文应用蒙特卡罗方法 （Monte-Carlo法，简称MC法）求解。

MC 法属于试验数学，它利用随机数进行统计试验，以求得均值与概率等统计特征值作为代解问题的数值解。该方法的主要思路是：按照概率定义，某事件的概率可能用大量试验中该事件发生的概率估算。因此，先对基本随机变量的分布函数FXi(xi)进行N次随机抽样，获得各变量的随机数x（jij=1，…，N），然后把这些抽样函数值代人功能函数式，得N个Zj值（j=1，…，N），统计Zj＜0 的失效次数Nf，并算出失效次数与总抽样次数的比值，此值即为所求的风险值的无偏估计量。

当样本容量N足够大时，MC 法的精度可由大数定理和中心极限定理求得［20］：

式中：ε为与Rf的相对误差。

由公式（7）可知蒙特卡罗方法的样本容量N与置信度1 -α、相对误差ε和风险值的无偏估计量均有关。在置信度确定的情况下，为使得风险值趋于稳定且相对误差较小，应取尽可能大的N。一般而言，采用蒙特卡罗法求解问题，往往需要数千乃至数万次的模拟计算。

3 工程实例应用

3.1 研究区域概况

岗前渡槽位于江西省赣抚平原灌区，跨越清丰山溪排洪道，具体地理位置见图1。岗前渡槽是江西省最大的渡槽，作为岗前水利枢纽的重要组成部分，主要承担灌溉、供水和航运等功能，渡槽于1958年冬动工兴建，1959年7月开始通水使用，在此期间渡槽促进了当地工农业生产，并且抵御了1982年特大洪水，在地区经济社会发展中发挥着举足轻重的作用。

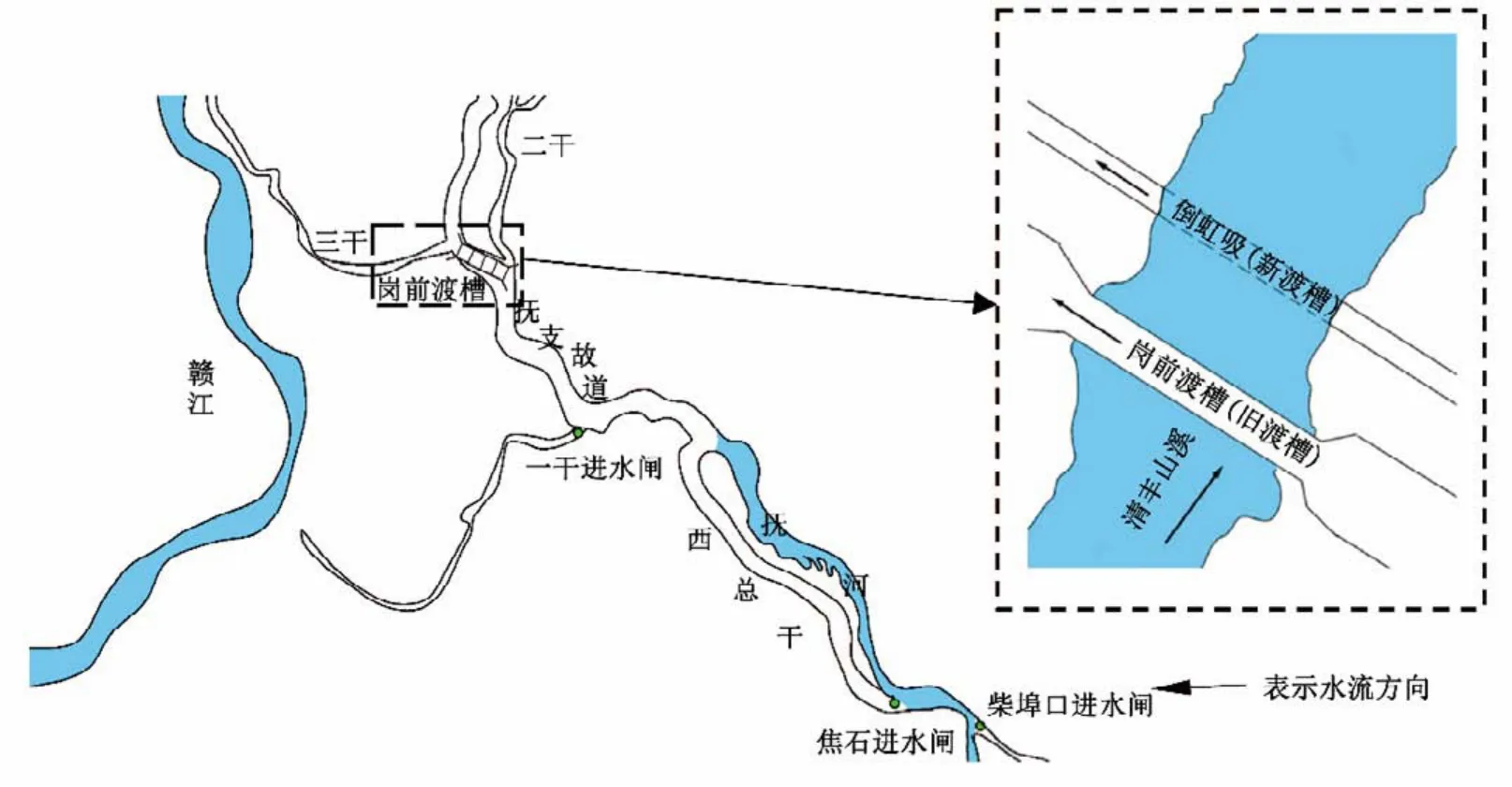
图1 赣抚平原灌区水系分布及岗前渡槽位置示意图Fig.1 Schematic diagram of drainage system distribution and position of Gangqian Aqueduct in Ganfu Plain Irrigation Area

但岗前渡槽运行60 余年，逐渐出现混凝土老化剥蚀、槽身开裂漏水、槽下淤泥堆积导致净空不足等安全问题，在2020 年4月《江西省赣抚平原灌区岗前渡槽安全鉴定报告》中被定性为四类渡槽，无法满足设计条件下的安全运行。2020 年9 月江西省水利厅、江西省发展和改革委员会决定采取在岗前渡槽下游侧（清丰山溪）66 m 处修建一个埋式倒虹吸作为新渡槽，以替代岗前渡槽在灌区中的供水及灌溉功能，现状岗前渡槽（简称旧渡槽）只承担航运功能。

3.2 输入资料及参数分析

新旧渡槽的工程设计参数和现状运行参数见表1。表1 中具体数据均来自《江西省赣抚平原灌区“十四五”续建配套与现代化改造（二期）可行性研究报告》。其中，新渡槽采取3 根4.2 m×4.2 m 的矩形管道，且最大过水流量为113 m³/s，报告中均称其为新渡槽的加大流量，因此本文新渡槽的加大流量取值为113 m³/s，见表1。

表1 新旧渡槽的有关参数Tab.1 Related parameters of the old and new aqueducts

依据报告确定渡槽的特征水位和特征流量后，考虑到岗前渡槽过水断面为矩形且坡度i=0.000 1，运用公式（5）建立旧渡槽特征水位与特征流量的对应关系，具体数据见表2。

表2 旧渡槽特征水位和特征流量的对应关系Tab.2 Correspondence between characteristic water level and characteristic discharge of the old aqueduct

报告指出“现状岗前渡槽运行水深不超过2.0 m 时（大于Ⅵ级航道最低运行水深1.0～1.2 m），渡槽结构满足安全运行要求”，故令旧渡槽正常运行的最高水位是23.48 m。同时报告中写明“现状岗前渡槽在遭遇清丰山溪20 年一遇设计洪水时，槽内水位低于23.95 m 时槽身的抗滑、抗倾稳定均不满足规范要求”，因此，公式（1）中的渡槽能维持防洪安全运行的最小流量为旧渡槽水位23.95 m对应的流量值，即取值为27.4 m³/s。新渡槽作为续建工程，需要承担除航运外的各项功能并保障旧渡槽的工程安全，公式（1）中的渡槽设计洪水流量为设计流量74.5 m³/s，具体数据见表2。

利用公式（2）～（4）计算洪峰流量Qm的P-Ⅲ型分布和正态分布。渡槽本身流量数据不足，但临近的吴石水文站拥有较为完整的60 年流量数据，考虑到赣抚平原属于小流域，所以可以综合渡槽已知数据和吴石站的水文数据确定设计洪水的参数，用样本统计参数近似替代总体的统计参数可得：均值EX=68.23 m³/s、偏态系数Cs=1.89、变差系数Cv=0.63。将上述参数代入公式（2）～（4），得到两种分布的密度函数图像如图2所示。

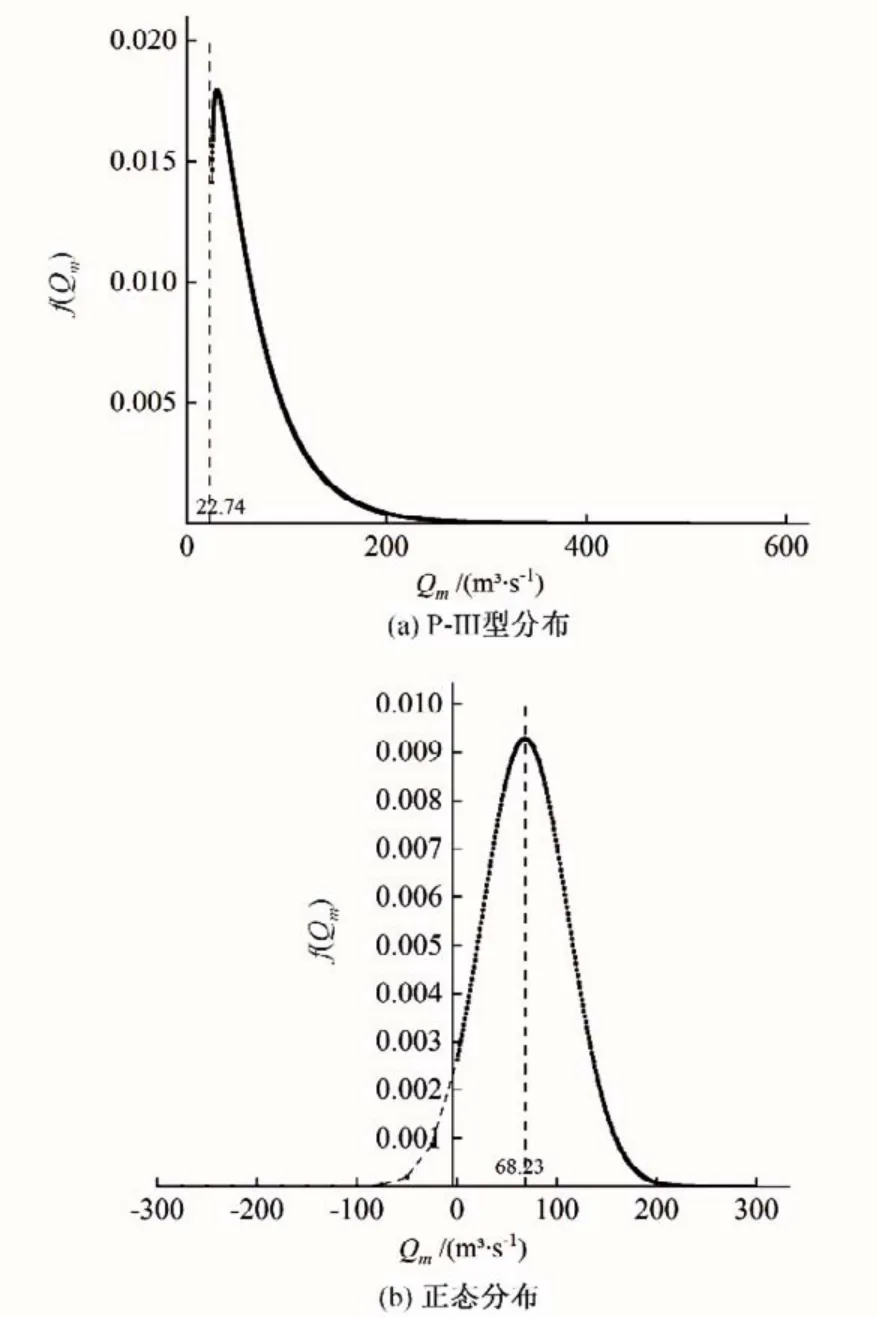
图2 洪峰流量Qm的P-Ⅲ型分布和正态分布图像Fig.2 P-Ⅲ distribution and normal distribution of Qm

图2（a）为洪峰流量Qm符合P-Ⅲ型分布的概率密度函数图像，图中虚线为Qm= 22.74 =a0，为图像的渐近线。图2（b）为洪峰流量Qm符合P-Ⅲ型分布的概率密度函数图像，图中虚直线表示Qm= 68.23 =EX，为图像的对称轴；图中的虚曲线表示Qm＜0，不符合实际情况，故用虚线表示。

从岗前渡槽2011-2018 年的历史流量数据中，选取最大15日流量作为典型洪水过程，以1 h 为一个时段绘制典型洪水过程线，具体见图3。

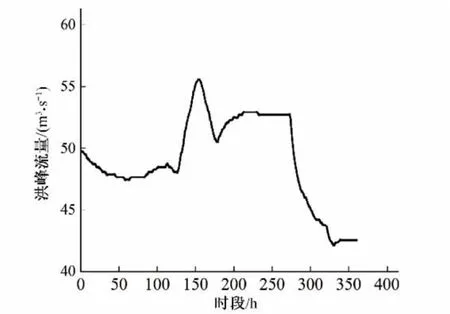
图3 典型洪水过程图Fig.3 Typical flood process diagram

3.3 渡槽防洪风险计算

考虑到渡槽本身结构的脆弱性和极端降雨事件的突发性，本文采取超过现状设计洪水的洪水流量来计算新旧渡槽协同防洪风险。

根据MC法原理，利用Matlab R2020b编程得到符合P-Ⅲ分布的伪随机数Qm，p-Ⅲ和符合正态分布的伪随机数Qm-φ，要求生成的伪随机数均大于旧渡槽现状防洪安全最小运行流量与新渡槽设计流量之和101.9 m³/s，即模拟高于现状设计流量的较为不利的洪水情景，以伪随机数作为设计洪峰，运用“峰比”放大法放大典型洪水，计算对应的设计洪水过程线。

采用公式（1），分别计算8 种情景下渡槽承担的防洪风险，结合公式（6）～（7）以及程序运行的效率和数据的收敛效果确定随机模拟次数，最终得到新旧渡槽防洪风险具体见图4和表3。

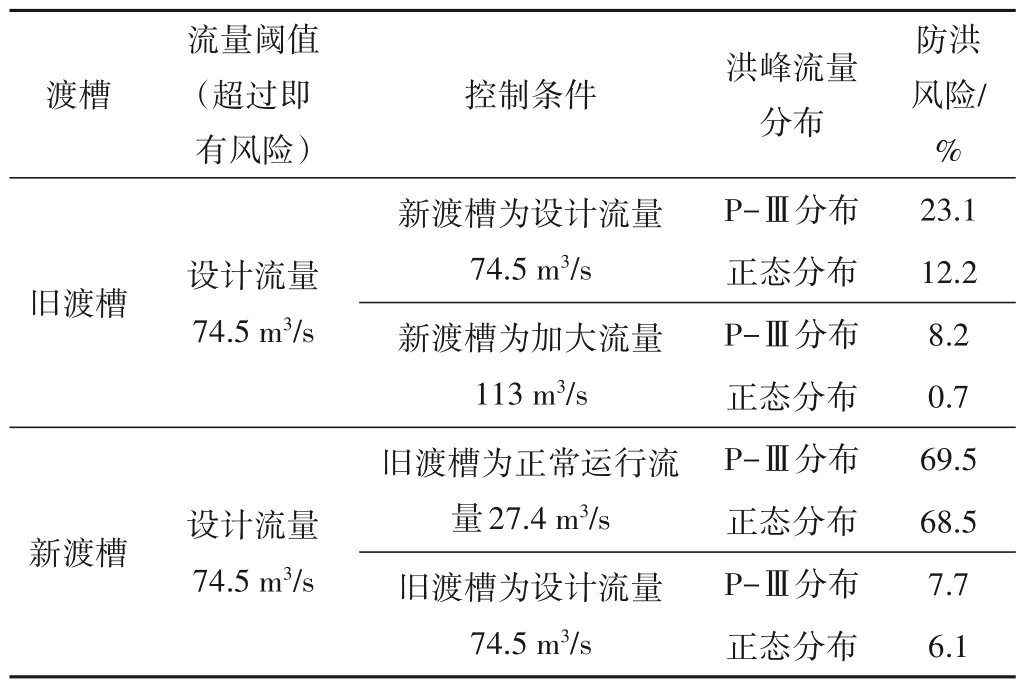
表3 MC法模拟新旧渡槽防洪风险的收敛结果Tab.3 Convergence results of MC method to simulate flood risks of the old and new aqueducts

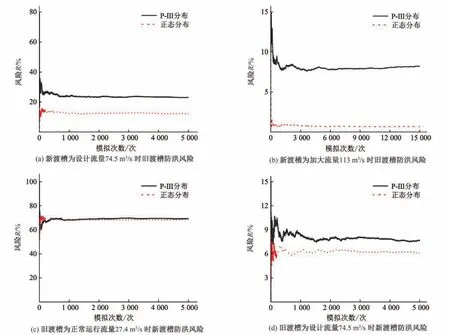
图4 模拟次数与渡槽防洪风险关系图Fig.4 Relationship between simulation times and aqueduct flood risk

图4（a）表示新渡槽流量为其设计流量74.5 m³/s 时，若洪峰流量分布分别满足P-Ⅲ分布和正态分布，经过5 000 次随机模拟后，旧渡槽所承担的防洪风险分别稳定在23.1%和12.2%；图4（b）表示当新渡槽流量为其加大流量113 m³/s 时，若洪峰流量分布分别满足P-Ⅲ分布和正态分布，经过15 000 次随机模拟后，旧渡槽所承担的防洪风险分别稳定在8.2%和0.7%。图4（a）、（b）比较表明，当超过现状设计流量的洪水来临时，让新渡槽按加大流量运行可以大幅降低旧渡槽的防洪风险。

图4（c）表示旧渡槽流量为其正常运行流量27.4 m³/s 时，若洪峰流量分布分别满足P-Ⅲ分布和正态分布，经过5 000 次随机模拟后，新渡槽所承担的防洪风险分别稳定在69.5%和68.5%；图4（d）表示当旧渡槽流量为其设计流量74.5 m³/s时，若洪峰流量分布分别满足P-Ⅲ分布和正态分布，经过5 000 次随机模拟后，新渡槽所承担的防洪风险分别稳定在7.7%和6.1%。图4（c）、（d）比较表明，超过现状设计流量的洪水来临时，让旧渡槽按照设计流量泄洪可以有效降低新渡槽超设计流量运行的风险。

表3 展示了8 种情景下渡槽的防洪风险，由表3 中数据可知：当新渡槽按加大流量运行时，两种不同的洪峰分布下，旧渡槽的防洪风险分别降低了64.5%和94.3%；当旧渡槽按设计流量运行时，两种不同的洪峰分布下，新渡槽的防洪风险分别降低了88.9%和91.1%，体现出新旧渡槽协同防洪的重要性和有效性。

在其余条件相同的情况下，P-Ⅲ分布的计算结果比正态分布平均偏高40.2%，说明洪峰分布采取P-Ⅲ分布可以模拟更加不利的洪水条件，在工程设计施工和后期运行时运用该分布确定设计和运行的参数，可以提升工程的安全性。

4 结 论

本文提出了新旧输水渡槽协同防洪风险分析方法，以江西省赣抚平原灌区的新旧输水渡槽为例，得出以下结论。

（1）选取超过20 年一遇标准的设计洪水作为流量输入，若新渡槽为设计流量74.5 m³/s，经过5 000 次随机模拟，旧渡槽防洪风险值趋于稳定，若新渡槽为加大流量113 m³/s，需经过15 000 次随机模拟，旧渡槽防洪风险才达到稳定值，说明蒙特卡罗方法受变量和风险大小的制约，需要增加模拟次数以提高精度。

（2）渡槽洪峰流量分布拟合采用了P-Ⅲ分布和正态分布两种函数，在其余条件相同的情况下，P-Ⅲ分布计算结果得到的渡槽防洪风险均比正态分布高，说明在工程设计施工和后期运行的情况下，洪峰分布采取P-Ⅲ分布可以模拟更加不利的洪水条件，提升工程的安全性。

（3）渡槽遭遇的洪水超过20 年一遇防洪标准时，旧渡槽若按正常运行流量27.4 m³/s 泄洪，则新渡槽承担防洪风险过大（约为70%）；若新旧渡槽均按设计流量74.5 m³/s 泄洪，则旧渡槽仍存在较大的防洪风险（约为18%），故应适时令新渡槽按加大流量泄洪，使旧渡槽防洪风险大幅降低，达到新旧渡槽协同防洪的效果。

灌区现有的水利设施经过长期运行，存在不同程度的安全问题，难以满足设计条件下的安全运行，续建新工程代替其部分功能是解决方法之一。研究新旧渡槽协同防洪对于其他现有水利工程和新建工程协同防洪有重要的参考价值。面临超设计标准的洪水时，分配新旧工程承担洪水量的大小会导致不一样的工程防洪风险，对此进行评估有利于后续制定新旧工程协同调度规则，维护工程正常运行管理。