缓冲包装不确定性的可靠设计与优化

安雪, 黄博文, 史冬岩

(1.哈尔滨工程大学 机电学院,黑龙江 哈尔滨 150001; 2.罗格斯新泽西州立大学 机械和航天学院,新泽西州 美国 08854)

不确定性问题存在于工程各个领域[1-3],然而,针对包装工程中的不确定性问题研究相对较少。本文对包装工程中缓冲防护结构的不确定性展开研究。

产品在搬运和运输过程中,由于存在诸多不确定因素,例如缓冲包装材料加工尺寸、产品储存温度和运输条件等,从而导致大量的包装产品破损[4-6]。为此,人们提出了许多方法保护产品使其远离损坏的危险。传统上,减少产品损坏方法是根据ASTM[7]提出的缓冲包装曲线对产品的缓冲防护结构进行设计。然而这种方法经常出现“过度设计”的情况,造成了材料的经济浪费。另外,缓冲曲线的确定需要进行大量的跌落实验,进而对实验数据进行拟合,数据越多,曲线的拟合精度就约高,浪费了大量的时间成本。这些缺点促使学者引入一种替代传统跌落实验的方法,该方法依赖于缓冲包装材料动态的本构关系[8-9],简化确定缓冲包装曲线的过程。然而,动态的本构关系仅对闭孔缓冲包装材料具有良好的缓冲性能[10],对于开孔的缓冲包装材料具有一定的局限性。另一种减少产品损坏的方法是对产品的包装系统进行力学建模,如线性或非线性单自由度或二自由度系统[11-12],通过对产品在跌落过程进行振动响应分析,使产品在跌落时产生的峰值响应加速度降低到产品的脆值(产品的固有属性)以下。

基于可靠度的优化设计(reliability-based design optimization, RBDO)是解决工程中不确定性的主要手段,得到了广泛地应用[13]。RBDO概率模型由最小目标函数和概率约束条件组成,以寻求最佳的工程设计,同时降低材料成本[14]。功能度量法(performance measure approach, PMA)[15]和可靠度指标法(reliability-based design optimization,RIA)是求解RBDO概率模型的2大主流方法。RIA方法是求解RBDO概率模型主要技术手段,但当遇到强非线性函数时,RIA方法会产生收敛失败和数值奇异解的现象[16-17]。

本文通过定义主动集合策略,提出一种改进的RBDO方法,克服了传统RIA方法的缺点同时解决包装工程中的不确定性问题。将得到的最优解采用蒙塔卡罗法(Monte-Carlo simulation,MCs)进行验证,并提供了一种方便简单的缓冲包装防护设计方法,实现质量和成本之间的平衡。

1 基于可靠度的优化设计

1.1 RBDO的数学模型

RBDO的数学模型为:

(1)

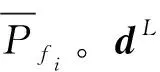
在可靠度理论中,通常采用统计模型来计算系统的失效概率:

(2)

式中fX(x)是X的联合概率密度函数。式(2)需要求解多维积分得到系统的失效概率。然而,对于大多数实际工程问题,求解多维积分是非常困难的,甚至是不可能完成的。

可靠度指标克服求解多维积分的困难[18],在标准正态空间内原点到功能函数曲面的最短距离,可靠度指标βHL为:

(3)

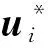
可靠度指标取值均为正,没有考虑负可靠度指标的情况。因此,可靠度指标的定义是导致RIA方法收敛困难和数值不稳定的主要原因。

1.2 修正的可靠度指标

针对传统RIA方法不收敛和数值不稳定的现象,本文对传统可靠度指标的定义进行修正。

本文采用一个逻辑不等式定义一个主动集合策略(active set strategy,ASS)实现对MPP点的过滤和识别,数学表达式为:

(4)

图1 MPP和±6σ之间的关系Fig.1 The positional relationship between MPP and ±6σ

对于大多数工程问题,如果设计变量落在±3σ范围内,则认为是可接受的设计,该设计称为3σ设计。该情况系统的可靠度为99.73%,失效概率为0.27%,如表1所示。然而,由于实际工程系统中存在各种不确定因素的扰动,对于大型复杂的工程结构,3σ设计则被认为是一种不充分和不可靠的设计水平。所以,本文选择6σ水平设计,其规定范围相当于99.999 999 8%的可靠度和0.000 000 2%的失效概率,远远优于其他设计水平。

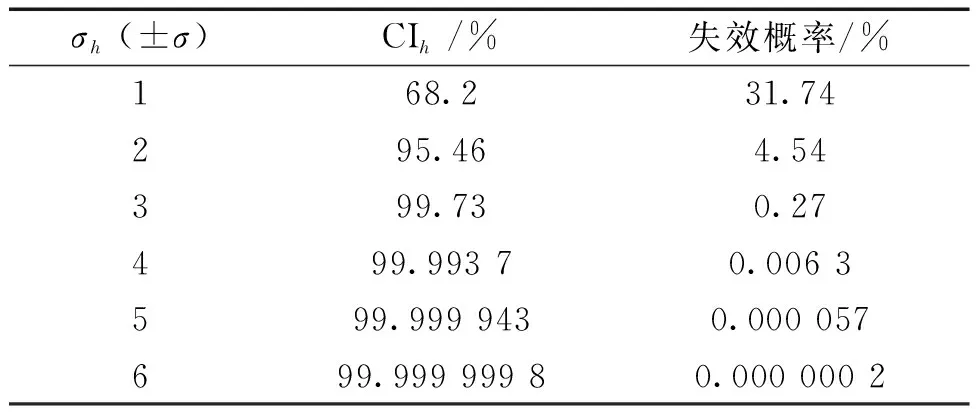
表1 不同的σh对应的CIh和失效概率Table 1 CIh and probability of failure for various σh

修改的可靠度指标重新定义为:

(5)

2 基于主动集合策略的可靠性设计优化方法

在式(1)中定义的RBDO问题,在求解过程通常采用双循环求解策略,即内循环和外循环,内循环是在独立的标准正态随机空间(U-空间)中进行可靠性分析,外循环是在原始物理空间(X-空间)中进行结构优化分析。在本节中,将分别详细的介绍内循环和外循环,这是本文提出方法的基础。

2.1 内循环

由于内循环主要是在U-空间执行一个次优化问题来确定MPP和可靠性指标βsj,因此,首先应使用转化公式将所有随机变量从最开始的空间转换为标准正态分布空间,如图2所示。

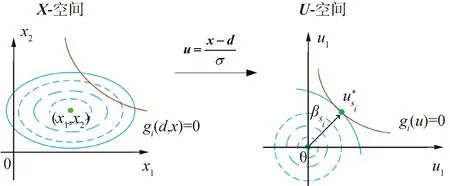
图2 X空间转化到U空间Fig.2 The X-space mapping to the U-space

(6)

其次,求解MPP执行的是一个次优化过程,其优化格式表示为:

(7)

式中:gj(u)是第j个有效约束条件的功能函数。借助于MPP后,将概率约束条件使用Rosenblatt[21]变换公式转化为确定性约束条件:

(8)

式中Φ是标准正态累积分布函数(CDF),因此,

(9)

(10)

根据式(9)和式(10)可以完成约束条件的转换,式(1)重新写成:

(11)

2.2 外循环

(12)

(13)

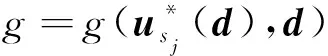
(14)

结合式(5)、(11)和(14)可得到最终的优化迭代格式为:

(15)

在优化开始之前,给出初始设计点d(0)和u(0)。对于每次迭代,首先执行式(7)完成内循环,以求解MPP点和可靠度指标。其次执行式(15)完成外循环,并更新内循环的解,直到程序收敛到最优解。迭代收敛标准‖d(k+1)-d(k)‖/d(k+1)≤ε(ε为给定的极小值),否则,当迭代次数大于允许次数时,则迭代停止。

3 缓冲包装防护结构的不确定性研究

3.1 包装系统的跌落模型

包装件通常由产品,缓冲材料和外包装箱组成,如图3所示。将产品和缓冲材料被理想化为具有刚度系数k的无阻尼非线性质量弹簧系统[22-23],本文忽略了外瓦楞纸箱,产品的质量用m表示。

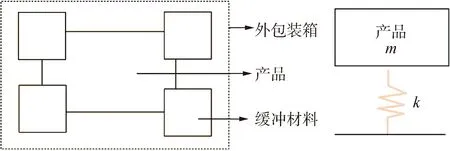
图3 包装产品的示意Fig.3 Graphic of a packaged product

包装系统的跌落模型如图4所示,其中h为跌落高度,t为缓冲保护材料的厚度。本文采用具有良好的缓冲性能闭孔泡沫聚苯乙烯(EPS)作为缓冲材料[24]。缓冲包装材料的非线性本构关系是通过压缩实验机获得压缩数据,并将数据进行多项式拟合确定,实验装置如图5和6所示。

图4 模型与地面撞击过程Fig.4 The process of collision between model and the ground

图5 压缩试验机5566Fig.5 Instron 5566

图6 缓冲材料和压盘Fig.6 The cushion material and platen

3.2 跌落过程中的能量分析

在跌落过程中,当包裹与地面碰撞时,缓冲包装材料被压缩为动态非线性变化过程。假设在动态冲击过程中,冲击产生的能量全部被缓冲材料吸收并使其变形最大不再传递到外界(忽略摩擦力的影响)。因此,本文以产品m为研究对象,由能量平衡得:

(16)

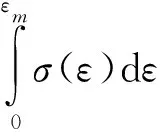
图7 动态的应力-应变曲线Fig.7 Dynamic stress-strain curve

进而计算出产品的最大加速度为:

amax=σ(εm)A/m

(17)

3.3 RBDO 数学模型

(18)

在本文中,初始设计点设置为d(0)=0.05和u(0)=0。优化收敛标准为ε=10-6,且给定的最大迭代步数是200次。

应用本文提出的ASS方法对上述数学模型进行计算求解。在评估概率约束的过程中需要迭代18次,收敛得到的最优解为0.036 0,其迭代过程如图8所示。此外,应用MCs验证最优解,随机抽取2×106个样本点对失效概率进行评估,2个约束的失效概率均在允许的失效概率(3%)内。因此,ASS解决了缓冲防护结构的厚度不确定性问题,并提供了缓冲包装防护结构的最佳厚度尺寸是0.036 0 m。

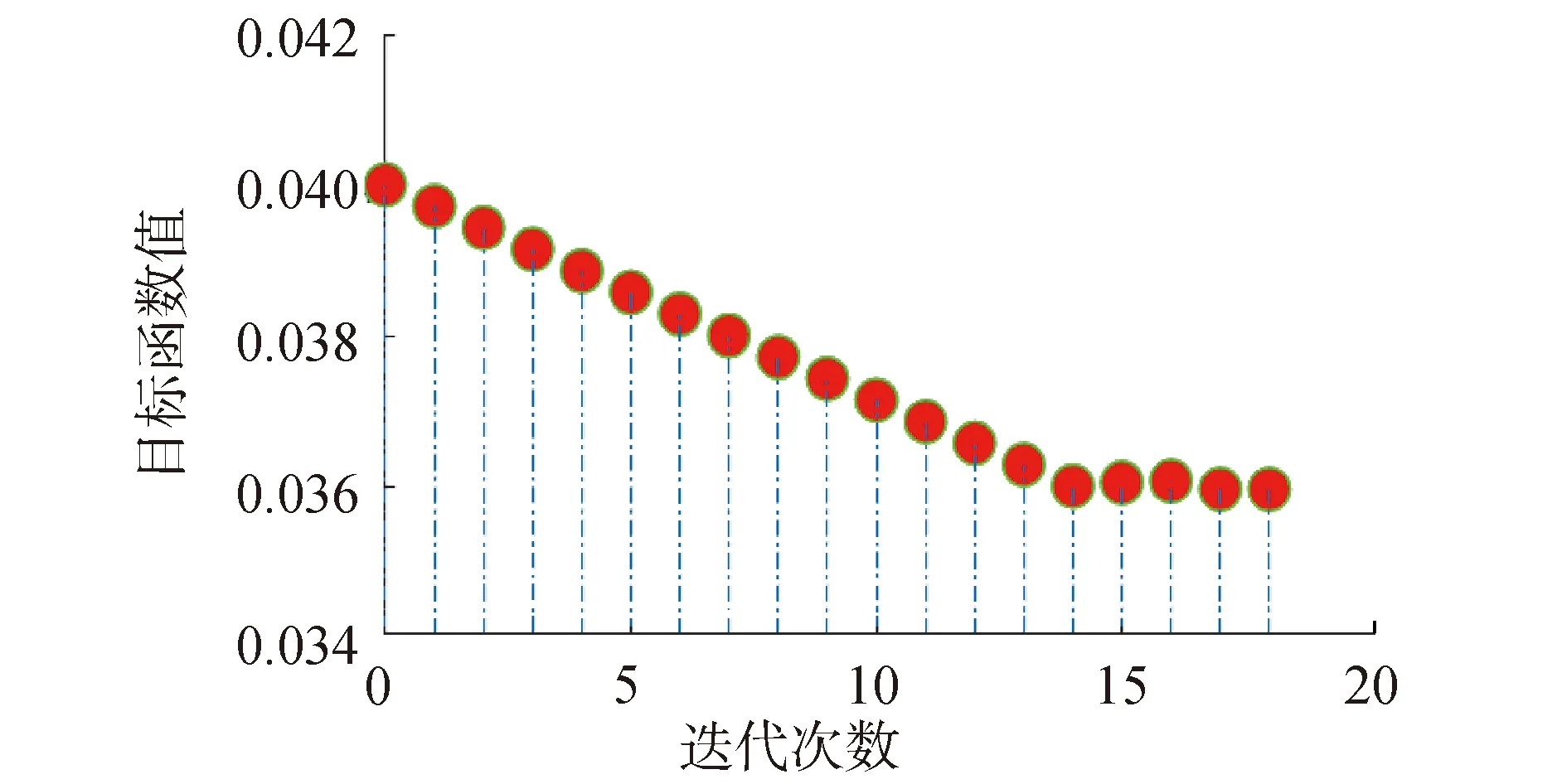
图8 迭代过程Fig.8 The process of iteration

4 结论

1)本文提出基于主动集策略的可靠度优化方法。通过在内循环中使用一个逻辑的不等式引入了主动集合策略对传统可靠度指标的定义进行修正,解决了传统RIA方法收敛困难和数值奇异性问题。

2)本文提出的ASS方法解决了包装工程中的不确定性问题。该方法充分考虑了缓冲包装防护结构厚度几何尺寸的不确定性因素,基于能量守恒建立了缓冲包装防护结构动态非线性的本构关系模型,通过将不确定性进行量化,构造了RBDO概率模型,并运用本文提出的方法计算出了全局最优解。最后,采用MCs方法对最优解进行验证,结果表明计算出的最优解是正确并且是合理的。

3)本文提出的方法为缓冲包装防护结构的轻量化设计和可靠性设计提供了理论支撑。