基于遗传神经网络的舰船磁场等效源重构方法
王毅, 周国华, 武晓康, 朱雪莲
(海军工程大学 电气工程学院,湖北 武汉 430033)
对于舰船磁隐身而言,准确预测舰船磁场的空间分布至关重要[1-2]。目前,存在多种预测模型,最常用的是等效源模型,包括磁单极子、旋转椭球体、磁偶极子、旋转椭球体与磁偶极子混合模型等。影响等效源模型预测效果的因素很多,重要的是等效磁源的参数设置,包括磁源的数量和位置。张朝阳等[3-4]采用粒子群、模拟退火等算法,对等效磁源的数量和位置进行优化设计,获得了舰船磁场预测模型,该类模型存在计算量大、预测结果不稳定的特点。郭成豹等[5]根据舰船的真实铁磁结构,设计了舰船等效磁源的三维空间分布,并利用Tikhonov正则化反演技术,对磁源数量和位置设置引起的病态问题进行了求解,实现了舰船磁场的准确预测,这种方法也存在建模复杂、正则化参数设置难等问题。
近年来,随着机器学习的不断发展,以数据挖掘和非线性预测为特征的人工神经网络被进一步开发,在电磁辐射领域得到广泛应用[6-8]。温军等[9]利用级联神经网络,建立了等效电磁偶极子混合模型,解决了未知电磁干扰源的辐射场预测难题。舒余飞等[10]利用人工神经网络,实现了复杂电磁环境下电子产品的等效辐射源的高精度建模。
本文以传统等效源模型为核心,借助人工神经网络的非线性预测和遗传算法的自适应寻优功能,提出利用遗传神经网络(genetic neural networks,GNN)[11-12]重构舰船磁场等效源的预测方法。通过多次学习训练,得到包含磁源信息的隐性等效源模型[13]。
1 遗传神经网络模型构建
1.1 传统等效源方法
根据铁磁性舰船空间分布,设置一定数量的磁偶极子,用这些磁偶极子代替舰船的真实磁源。在舰船坐标系下,磁偶极子坐标记为Qi(ui,vi,wi),空间任意点坐标记为Pj(xj,yj,zj),空间任意点的三分量磁场Bj(Bxj,Byj,Bzj)为:
(1)
式中:mui、mvi、mwi分别表示第i个磁偶极子沿x、y、z轴方向的磁矩分量;axji、ayji、azji、bxji、byji、bzji、cxji,cyji、czji表示空间系数。
将式(1)矩阵表示为:
G×M=B
(2)
式中:B表示舰船磁场矩阵;G表示磁场测量点与模拟体坐标之间的系数矩阵;M表示各模拟体的三分量磁矩组成的磁矩向量。
若已知舰船磁场测量平面,则系数矩阵G已知,把舰船近场磁场矩阵B代入式(2),即可反演得到舰船等效模拟体的磁矩信息M。在此基础上,根据目标区域的场点坐标,形成新的系数矩阵G1,由G1×M即可预测目标区域的磁场信息。
在利用上述方法预测舰船周围空间磁场时,由于难以获得磁偶极子的最佳数量和位置分布,式(2)将会变成一个不稳定的矩阵方程,求解磁矩向量M的反演过程无法严格成立,影响了舰船磁场预测效果。因此,本文提出利用人工神经网络的学习能力和遗传算法的自适应优化功能对等效源模型进行重构,避免反演求解过程,提高舰船磁场的预测精度。
1.2 遗传神经网络
1)人工神经网络[14-16]。
传统的等效源方法主要利用舰船磁场B逆推出等效模拟体的磁矩信息M。每个等效模拟体磁矩M的幅值、方向信息已知。本文将系数矩阵G作为人工神经网络的输入,舰船磁场B作为人工神经网络的输出,通过多次训练,得到一个隐性的等效源模型。磁矩信息M由人工神经网络的隐含层节点数、连接权值、阈值、传递函数等参数共同表示。输入信息(系数矩阵G)根据磁源计算公式推导,与输出信息(舰船磁场B)之间存在真实的非线性关系,显著提高神经网络的训练效率。
该网络采用梯度下降法进行训练,参数更新由神经网络的反向传播算法确定。在反向传播过程中,误差函数E为:
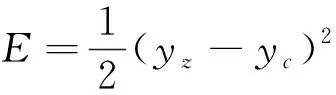
(3)
式中:yz表示训练集输出的真实值;yc表示训练集输出的预测值。
2)遗传算法[17-19]。
在利用人工神经网络进行预测建模时,各层的连接权值及阈值是随机初始化的。这种未经优化的权值和阈值,会降低人工神经网络的收敛速度,且容易陷入局部最优解。因此,考虑采用遗传算法对初始权值和初始阈值进行优化设计。
3)遗传神经网络训练流程[20-22]。
本文训练了3个遗传神经网络对舰船磁场纵向分量Bx、横向分量By、垂向分量Bz进行预测。由于结构和训练过程是相似的,所以仅以Bx预测为例描述该方法。
遗传神经网络流程如图1所示,其主要步骤为:
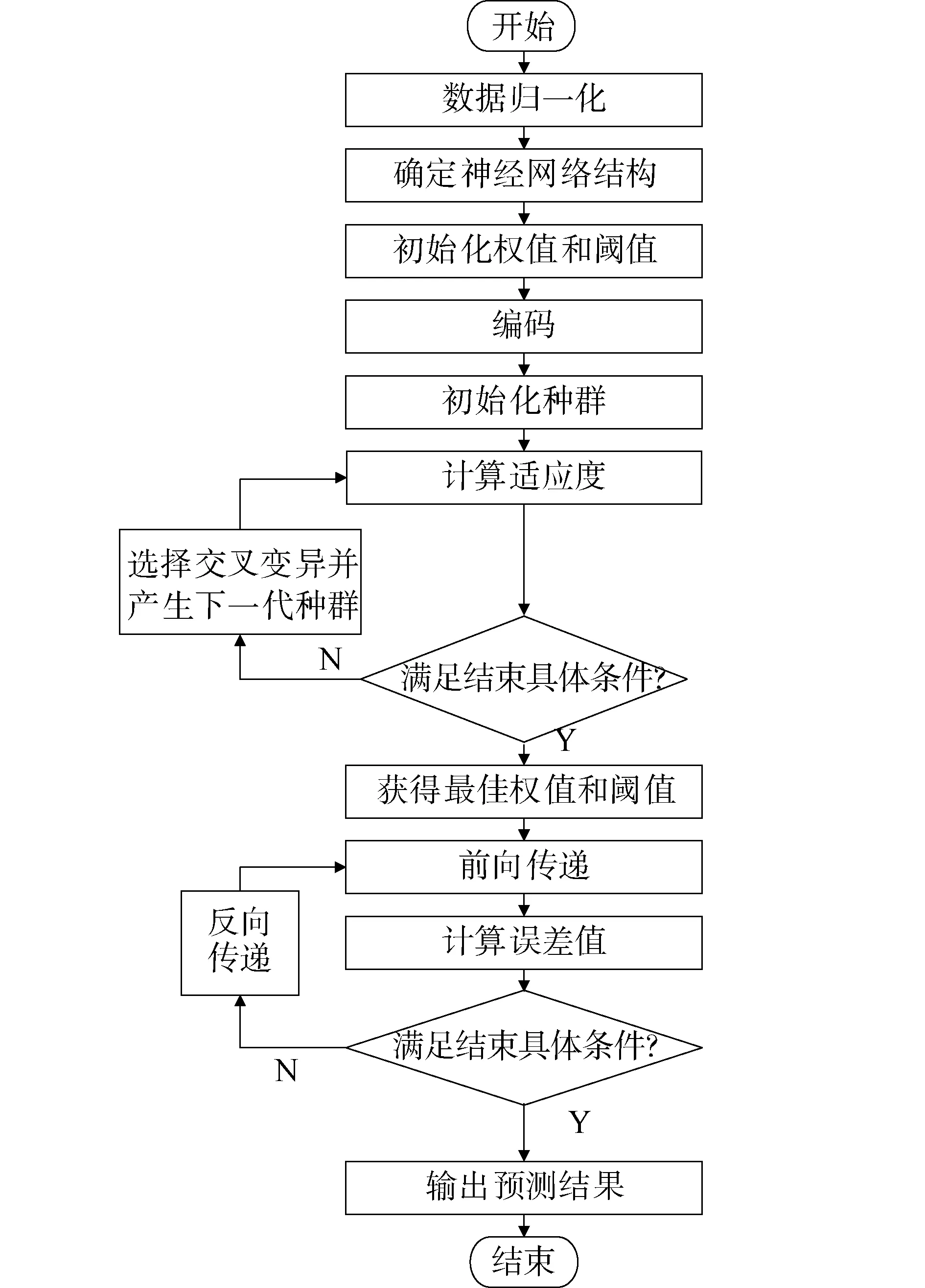
图1 遗传神经网络流程Fig.1 Genetic neural network processes

(4)
式中:xi表示输入或输出数据;xmax表示数据最大值;xmin表示数据最小值。
2)确定人工神经网络输入层、隐含层、输出层结构。
在本文中,输入层有3N个节点,表示设置了N个磁偶极子阵列模拟舰船磁场,每个磁偶极子对应扫描点都有3个空间系数(axji,ayji,azji);输出层有1个节点,表示该扫描点的舰船磁场分量Bxj。对于隐含层,通常根据经验公式,确定隐含层的节点范围:

(5)
式中:s为隐含层神经元个数;m和n分别为输入层、输出层神经元个数。
在获得隐含层神经元s范围的基础上,运行人工神经网络,计算不同s值的训练误差,把训练误差最小时的s值记为隐含层神经元个数。
3)遗传算法参数初始化。随机初始化人工神经网络的权值和阈值,并进行实数编码,生成用于遗传算法寻优的初始种群。在此基础上,设置遗传算法的最大进化代数、交叉概率、变异概率等参数。
4)执行选择、交叉、变异操作,不断更新遗传算法的适应度值,达到最大进化代数。适应度值最小的个体被搜索到,得到最佳的初始权值和初始阈值。适应度函数为:
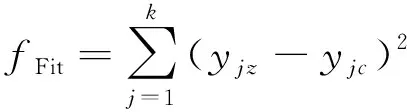
(6)
式中:yjz表示测试集输出的真实值;yjc表示测试集输出的预测值;k表示测试集的样本个数。
5)把遗传算法优化得到的最佳权值和最佳阈值,代入人工神经网络进行训练和测试,得到训练好的模型,算法结束。
2 船模仿真试验
2.1 数值模型
虚拟舰船船长L=4.2 m,船宽B=0.5 m,建立如图2所示的空间坐标系。在-1 950 mm≤x≤1 950 mm,y=0,z=0范围内,等间距设置了21个磁偶极子(“单条线阵列”)作为仿真试验的等效磁源。

图2 虚拟船模与6个测量平面Fig.2 Simulated ship model and six measuring planes
在虚拟船模的水线面下方750、1 000、1 500、2 000、2 500、3 000 mm设置6个深度平面。深度平面纵向长度为8 400 mm,纵向间隔100 mm;横向宽度为1 000 mm,横向间隔为250 mm,每个深度平面形成包含“5×85”个点阵的测磁阵列。
2.2 仿真训练过程
通过设置产生6个深度平面的磁场数据,每个深度平面都包含425个测量点,即425个样本数据。磁场数据包括磁矩计算值、测磁噪声:
1)磁矩计算值。为了获得虚拟舰船的磁场数据,另设计了单个旋转椭球体与5个磁偶极子的混合模型,用于代替该虚拟舰船;通过对该混合模型的磁矩信息进行赋值,可以获得混合模型在6个深度平面所有测量点的三分量磁场计算数据。其中,每个测量点的纵向分量|Bx|和横向分量|By|在20 000 nT以内,垂向分量|Bz|在40 000 nT以内。在对混合模型的磁矩信息进行赋值时,相邻磁矩变化应具有连续性,不能发生过强的突变;
2)测磁噪声。为了模拟真实情况,设定测磁阵列所在空间存在均匀分布的非相关随机噪声。取[-10 nT, 10 nT]范围内的随机值作为测磁噪声。
把深度平面1(z=750 mm)和平面2(z=1 000 mm)上的磁场数据作为GNN模型的训练样本。同时为了降低GNN的泛化误差,采用5折交叉验证方法,把训练样本数据随机分成5等分,每次取一等分做测试集,其余做训练集,由此可以得到5次试验的测试集的预测误差均值,以此控制GNN模型的训练过程。
在GNN完成训练以后,把另外4个深度平面上的系数向量输入训练好的模型,就可以预测指定平面的三分量磁场数据Bx、By和Bz。
2.3 结果分析
为评估模型预测精度,设相对误差Eerr为:
(7)
式中:Bpre表示预测值;Bt表示真实值或仿真值。
为了比较2种模型的预测效果,参考传统等效源模型,由深度平面1、平面2的磁场数据反演建模,并正演预测深度平面3、平面4、平面5、平面6的磁场值Bx、By和Bz。磁场预测结果如表1所示。
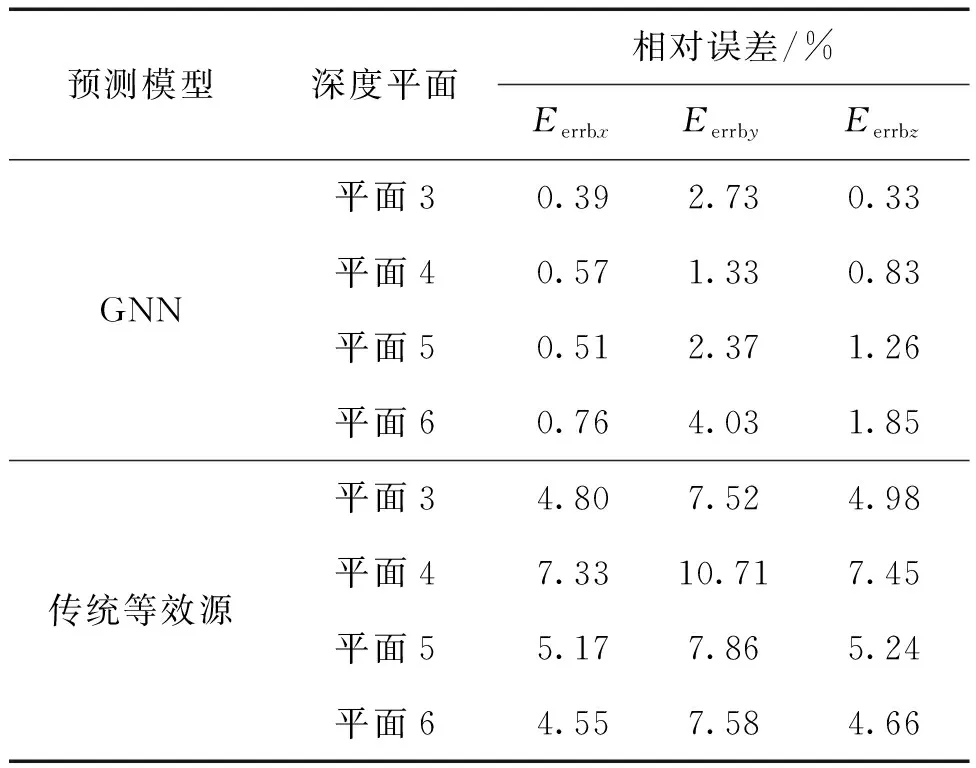
表1 仿真试验的预测结果Table 1 Prediction results of simulated test
从表1中可以看出:
1)对于GNN模型,预测Bx和Bz时,其在4个深度平面上均具有较高的预测精度,最大相对误差分别为0.76%和1.85%;预测By时,其在4个深度平面上预测精度较差,最大相对误差4.03%。
2)在磁源参数设置(数量和位置)相同的情况下,比较GNN与等效源模型对Bx、Bz的预测结果。GNN模型的预测精度均优于传统等效源模型。例如,在对最不利的深度平面6进行预测时,GNN模型对Bx和Bz的预测误差分别为0.76%、1.85%;传统等效源模型对Bx和Bz的预测误差分别为4.55%、4.66%。
3)比较2种模型对By的预测结果,GNN模型的预测精度优于传统等效源模型,但差距不大。以深度平面6的预测结果为例,GNN模型对By预测误差为4.03%;等效源模型对By的预测误差为7.58%。
3 物理模型试验
3.1 实验设计
选取了磁场实验室的一条物理模型(船长为L,船宽为B)进行实验。测磁阵列纵向长度为2L,纵向间隔1/42L(见图3);横向宽度为2B,横向间隔为0.25B,由此形成包括425个点阵的测磁平面,被测舰船位于测磁平面的中心位置。借助升降机调整测磁平面深度,获得船模下方1.5B、2B、3B、4B共4个深度平面的磁场数据。

图3 船模磁场测量面视图Fig.3 Ship model magnetic field measuring planes views
3.2 遗传神经网络训练过程
不考虑船模的几何特征,本文仅在水线平面的中线范围内(-0.5L≤x=≤0.5L,y=0,z=0),等间距均匀设置单条线磁偶极子阵列(简称“单条线阵列”),由29个磁偶极子构成,作为等效磁源,如图4所示。
图4 单条线磁偶极子阵列Fig.4 Single-line array of magnetic dipoles
把1.5B和2.0B深度平面上的磁场数据作为GNN模型的训练样本数据。同时为了降低GNN的泛化误差,采用5折交叉验证方法控制GNN模型训练过程。
在完成上述模型训练基础上,分别输入3B、4B深度平面的系数向量,按照图1所示流程,预测这3个深度平面的磁场值Bx、By和Bz。
3.3 结果分析
为了比较2种模型的预测效果,又利用传统等效源模型,由1.5B、2B的磁场数据反演建模,并正演预测3B、4B平面的磁场值Bx、By和Bz。评判标准采用式(3)所示的相对误差。磁场预测结果如表2所示。
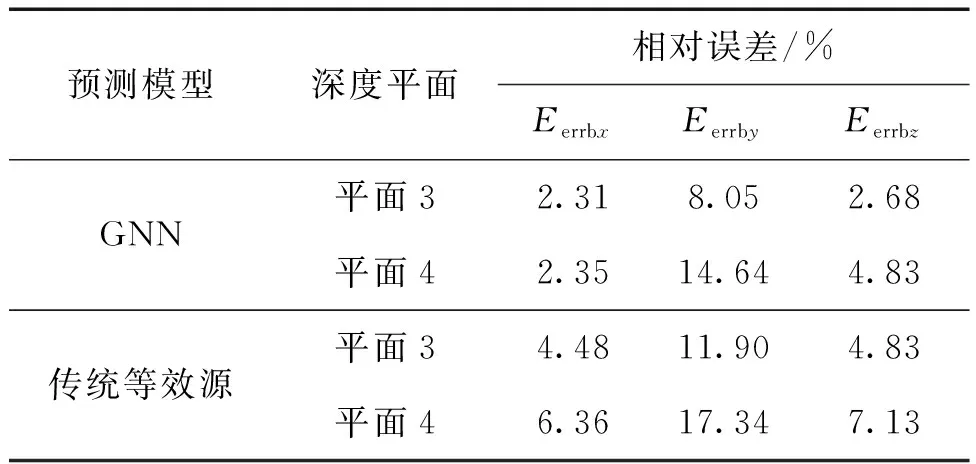
表2 船模试验的预测结果Table 2 Prediction results of ship model test
从表2中可以看出:
1)预测Bx和Bz时,GNN模型在2个深度平面上预测精度较高,其最大相对误差分别为2.35%、4.83%。
2)预测By时,GNN模型在2个深度平面上预测精度较差,最大相对误差14.64%。究其原因,是由于整个测量过程是在南北轨道上完成,船模磁场横向分量By较小,尤其是龙骨下的By值趋近于0(见图5),对GNN模型的学习训练产生不利影响,导致了磁场预测的相对误差较大。

图5 典型测量线上船模磁场预测值和真实值比较Fig.5 Comparison of predicted and real values of ship model magnetic field on typical measuring point line
3)对2种模型的预测结果进行比较,在预测Bx、By和Bz时,GNN的预测精度均优于传统等效源模型。例如,在对最不利的4.0B深度平面的磁场进行预测时,GNN模型对Bx、By和Bz的预测误差分别为2.35%、14.64%、4.83%,传统等效源模型的预测误差分别为6.36%、17.34%、7.13%。
取船模龙骨下方坐标x=-1L~+1L,y=0,z=+3B,+4B的3条典型测量点线,进行船模磁场预测值与真实值的比较,结果如图5所示。从图中可以看出,在预测Bx、By和Bz时,利用1.5B和2.0B的数据进行学习训练,并预测3.0B、4.0B深度平面的磁场值,吻合度较好,表明GNN模型能够实现船模磁场的精确预测,且预测精度由于传统等效源模型。
4 结论
1)本文建立的GNN模型,避免了传统等效源反演求解的不利影响,实现了船模磁场的准确预测。
2)GNN模型对船模磁场纵向分量Bx、横向分量By和垂向分量Bz的预测精度均优于传统等效源模型,且随着训练样本的增多,GNN模型的学习能力和预测精度还将进一步提高。
本文的研究结果为下一步开展实船磁场数据建模与预测奠定了基础。

