防淤积型透空式防波堤水动力特性分析

于通顺, 唐俊辉, 孟晓宇

(1.中国海洋大学 工程学院,山东 青岛 266000; 2.中国电力工程顾问集团东北电力设计院有限公司,吉林 长春 130021)

随着我国海洋生态文明建设的不断推进,对防波堤的环保属性提出了更高要求。传统堤身封闭式的防波堤阻断了港池内外水体交换,易引发港池内水质劣化[1],已不适应“蓝色海湾、银色沙滩”的建设需要。为解决传统防波堤的环保问题,透空式防波堤[2-3]应运而生,其水动力性能受到国内外研究人员的广泛关注,对于竖直板式透空堤的理论推导做了大量的工作。Ursell[4]根据修正的贝赛尔函数推导了有限潜深的竖直薄板在波浪作用下透射系数的解析解。Weigel[5]提出了透空式防波堤的理念,在忽略了波浪的绕射的前提下通过微幅波理论推导了竖直挡板式防波堤的反射、透射系数的解析解。邱大洪等[6]将波浪的绕射现象考虑在内,推导在任意水深下单一薄板式防波堤的透射、反射系数解析解,为后来有关板式防波堤的研究奠定了重要的理论基础。琚烈红等[7]在忽略波浪与防波堤相互作用过程中能量损耗的前提下引入了经验系数,基于波浪理论和能量守恒定律探究单层挡板透空式防波堤的透射系数解析解。朱大同[8]在考虑流体粘性情况下对单层竖直挡板防波堤的消波特性和受力特性展开研究。Смирнов[9]在Wiegel公式[5]基础上引入局部损失阻力系数,得到透射系数解析解,并给定了相应的适用条件,目前我国防波堤设计与施工规范中采用的公式与文献[9]推导一致。

防波堤水动力性能的模拟研究是透空式防波堤研发的重要内容。殷福安[10]采用物理模型断面试验方法给出了特定波浪条件下单层竖直挡板式防波堤透射系数的公式。Neelamani等[11]研究了由互相平行的2个竖直板组成的挡浪结构的水动力特性,分析2个板中间水体的波动,并基于结构物的消波效果,发现双侧挡板对不规则波的衰减作用较规则波更明显。文献[12-13]研究双侧挡板式透空式防波堤波浪要素、结构尺寸等对消波特性的影响。针对波浪作用过程中水质点做椭圆形运动的特点及透空式防波堤只对特定参数范围内的波浪有明显消波效果的特征,周效国等[14]设计一种多层直立挡板式防波堤,各挡板设置不同表面开孔率和底高程,其中下部挡板可以前后运动,对不同水位、波高和周期的波浪逐层消减。严以新等[15]对竖直多层挡板式挡浪结构进行物理模型试验,根据结果给出了设置4层挡板以及将挡板进行前排稀疏后排加密排列的建议。Rao[16]将挡板斜向布置,对倾斜角度不同的板式结构进行了全面的物理模型试验研究。

目前竖直挡板式防波堤的研究比较成熟,在国内已经成功得到应用[17-19]。然而港区频繁涨落潮过程中港池外泥沙会随水流大量进入港池内部,造成港池内泥沙淤积。针对这一问题,于通顺等[20]在竖直挡板式防波堤结构基础上,提出了一种防淤积型透空式防波堤。考虑到海水中泥沙主要集中在下层水体中[21],该防波堤在竖向桩柱底端设置下拦沙板,挡板下表面与海床紧密接触,在上部挡浪板后侧设置上拦沙板,挡板可沿桩柱表面滑道上下移动。当海水中泥沙含量较低时,上拦沙板全部隐藏在挡浪板后,当泥沙含量超过设定的阈值时,上拦沙板会沿着滑道下降,与下拦沙板对接在一起,将港池内外过水通道完全阻隔,避免泥沙进入港池内。

本文针对防淤积型透空式防波堤的水动力性能,采用数值模拟的方法开展研究。建立了波浪与防淤积型透空式防波堤相互作用的数值模型,开展物理模型试验以验证数值模型的准确性,基于数值模型考察了透空式防波堤的消波效果与受力特征。

1 水动力分析数值理论

本文基于流体连续性方程、动量方程和标准的k-ε紊流模型构建波浪与防淤积型透空式防波堤相互作用的数值模型。

连续性方程:

(1)

动量方程:

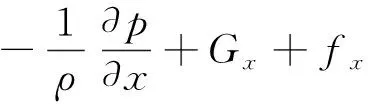
(2)

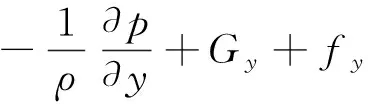
(3)

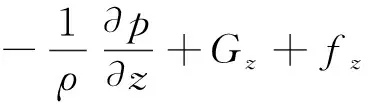
(4)

式中:u、v、w是x、y、z方向的流速;Ax、Ay、Az是x、y、z方向控制方程的各个波浪面积分项;VF表示控制方程的可流动体积分数;ρ为介质密度;Gx、Gy、Gz与fx、fy、fz为流体在三维空间中的重力以及粘滞力加速度;p为压力。

标准k-ε紊流模型为:

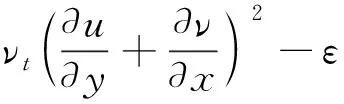
(5)

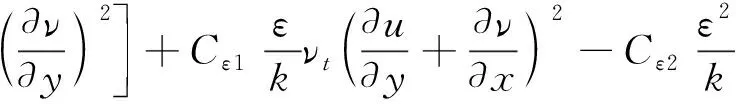
(6)

式中:k为湍动能;ε为耗散率;ν为运动粘滞系数,νt=Cuk2/ε为紊动粘性系数,标准的k-ε模型中的参数选择为Cε1=1.43,Cε2=1.92,σk=1.0,σε=1.3[22]。

本文采用基于界面重构技术的自由表面处理方法(volume of fluid method, VOF)[23]捕捉自由液面,根据不同时刻流体在网格单元中所占体积函数F的不同追踪自由液面的变化过程,可较好地捕捉自由液面破碎、冲击、翻滚等现象。

2 数值模型的建立

2.1 数值水槽建立

所建数值水槽长宽高分别为18、0.6、0.7 m。造波机设置在水槽x轴方向0 m位置,末端设置消波网,模型中心位于水槽x轴方向7 m处,模型前设置的2个监测点分别在模型前2 m和1.5 m处,模型后设置的3个监测点分别在模型后0.75、1和2 m处,用以监测模型前后自由液面的变化情况。数值模型及监测点的布置情况如图1所示。

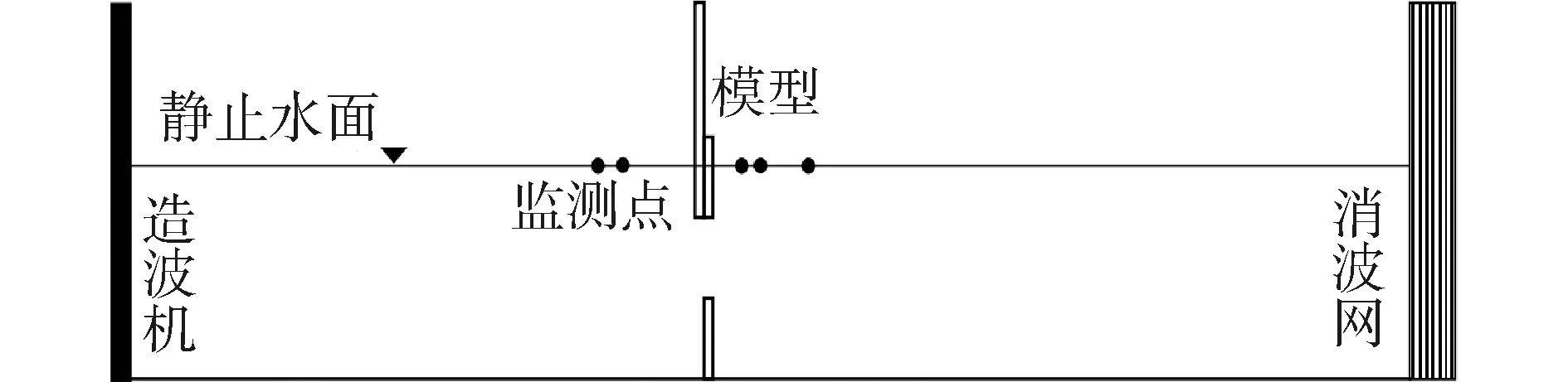
图1 波浪与防波堤相互作用数值模型示意Fig.1 Numerical model diagram of interaction between wave and breakwater

2.2 计算网格划分

将整个计算区域沿x轴方向分为3部分,第1部分0～6.7 m,第2部分6.7～7.3 m,第3部分7.3～18 m,并对第2部分防波堤结构所在区域和z方向波高附近网格进行加密,整个计算区域划分为15块,如图2所示。其中,块1、块2和块3的x方向网格尺寸为0.02 m,块4、块5和块6的x方向网格尺寸为0.01 m,块7、块8和块9的x方向网格尺寸为0.005 m,计算区域y方向网格尺寸为0.02 m,块1、块4和块7的z方向网格尺寸为0.01 m,块3、块6和块9的z方向网格尺寸为0.015 m。

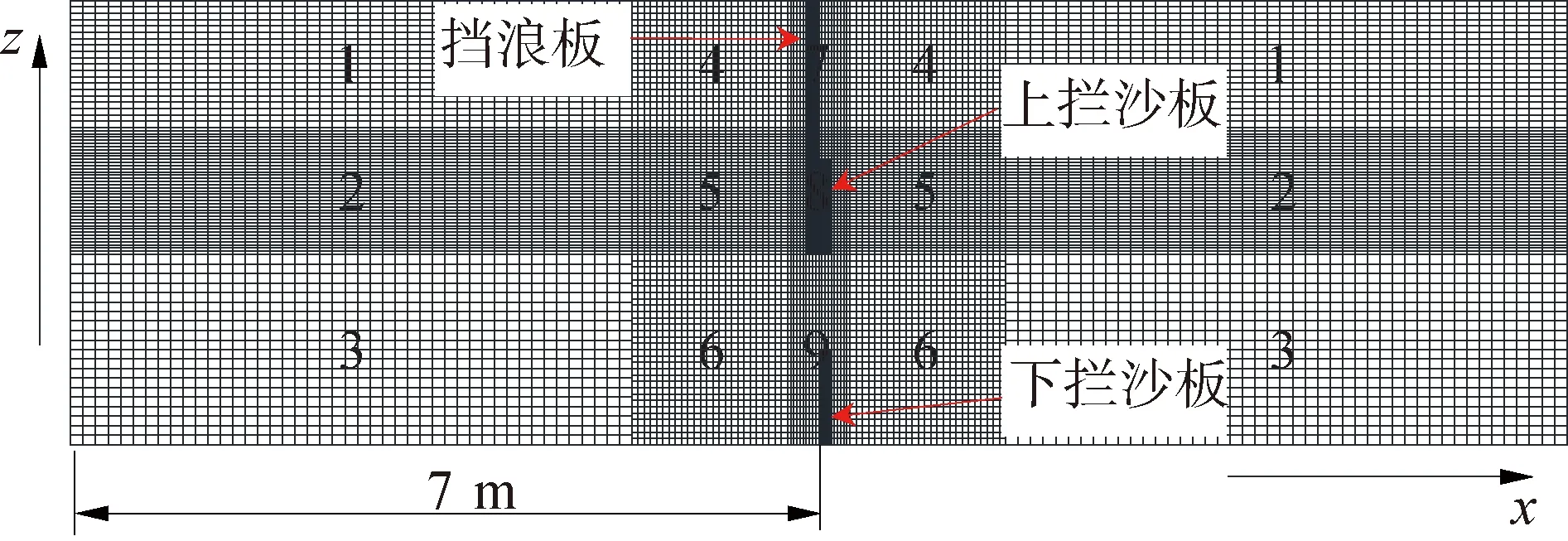
图2 防波堤网格划分示意Fig.2 Schematic diagram of breakwater grid division

2.3 模型尺寸及工况设计

《防波堤设计与施工规范》[24]规定,对基本不越浪的直立式防波堤,堤顶高程宜定在设计高水位以上不小于1.25倍设计波高处,当透空式防波堤采用单侧挡浪结构时,挡板入水深度与水深之比宜取0.3～0.5。基于广东海安新港荔枝湾码头[25]所在位置的水利条件和桩基透空式防波堤结构的建造尺寸,设计数值模拟的水利条件及防波堤的模型尺寸。模拟工况采用规则波,根据上拦沙板下落距离D的不同将模型分为3种结构形式。试验在水深0.4 m与0.45 m的2种条件下进行,波高范围为0.06～0.14 m,波浪周期为1.0～1.4 s,上拦沙板下落范围为0～0.10 m,组合不同的波浪参数共计64组工况。防波堤模型挡浪板的高度为0.4 m,当水深为0.4 m时,挡板初始入水深度为0.1 m,上、下拦沙板的高度均为0.15 m,挡板厚度为0.02 m,方形桩柱边长为0.06 m。

2.4 网格独立性和模型准确性验证

为了更精确地获取波高数据,需对z方向波高附近网格进行加密,因此首先要进行网格独立性验证。在波高范围内设置3种网格数量方案,分别为20、40和60。在三维水槽模型中对水深0.4 m,波高0.08 m,周期1.2 s波浪工况进行计算,比较3种网格尺寸下相同位置波面的历时曲线,结果如图3所示。比较后发现,3种方案在x-z方向上的网格最大纵横比都为2,网格数量为40与60的2种方案的计算结果基本吻合,仅在峰值和谷值处存在细微差别,网格数量20的方案与其他2种方案的计算结果差距较大。表1给出了不同网格设置方案下计算域的网格数量及求解器运行时间,综合考虑计算精度和时间成本,在波高范围内z方向划分的网格数量为40,因此块2、块5和块8在z方向网格尺寸为0.005 m。

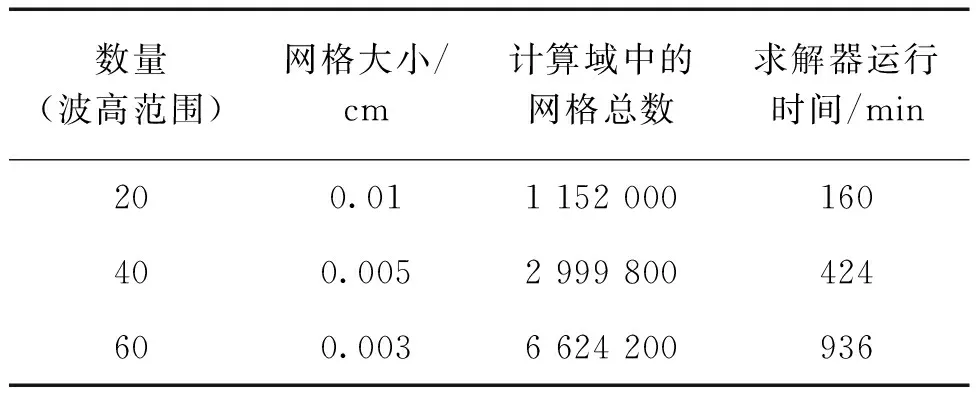
表1 三维数值水槽流体域计算精度与时间成本Table 1 Calculation accuracy and time cost of fluid domain in three-dimensional numerical flume

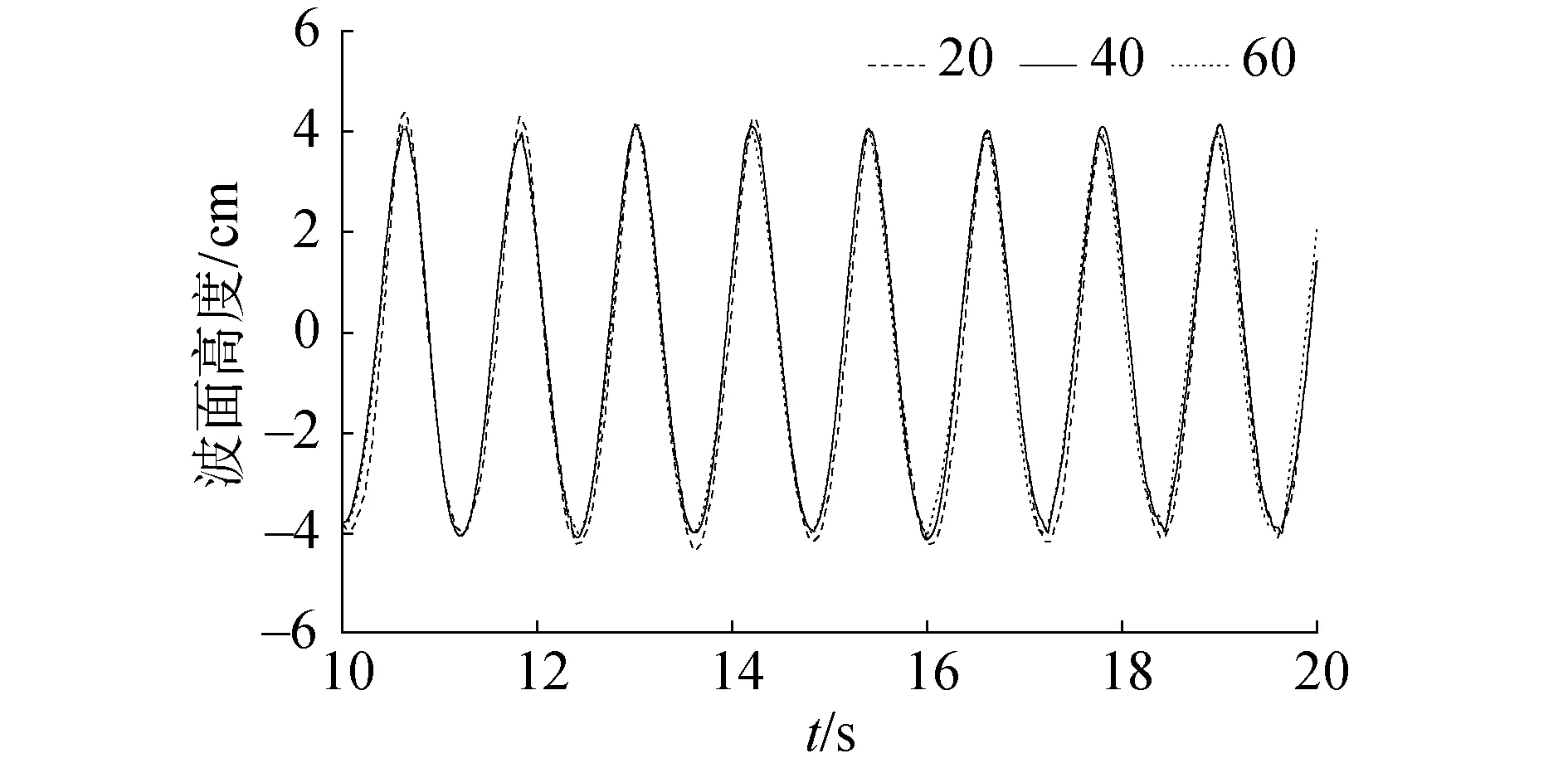
图3 不同网格尺寸的波面历时曲线Fig.3 Wave duration curves of different mesh sizes

提取x=7 m处的波高历时曲线,并将其与理论波形作对比,如图4所示。可以看出数值模拟的波浪与理论波形相比存在一定的变形,波峰处略尖陡,波谷处略平坦,在波面下降阶段,数值模拟结果相对理论值略小,但整体而言与理论吻合较好,表明本文所建立的数值水槽能产生持续稳定的规则波浪,数值水槽z方向液面附近网格划分合理。

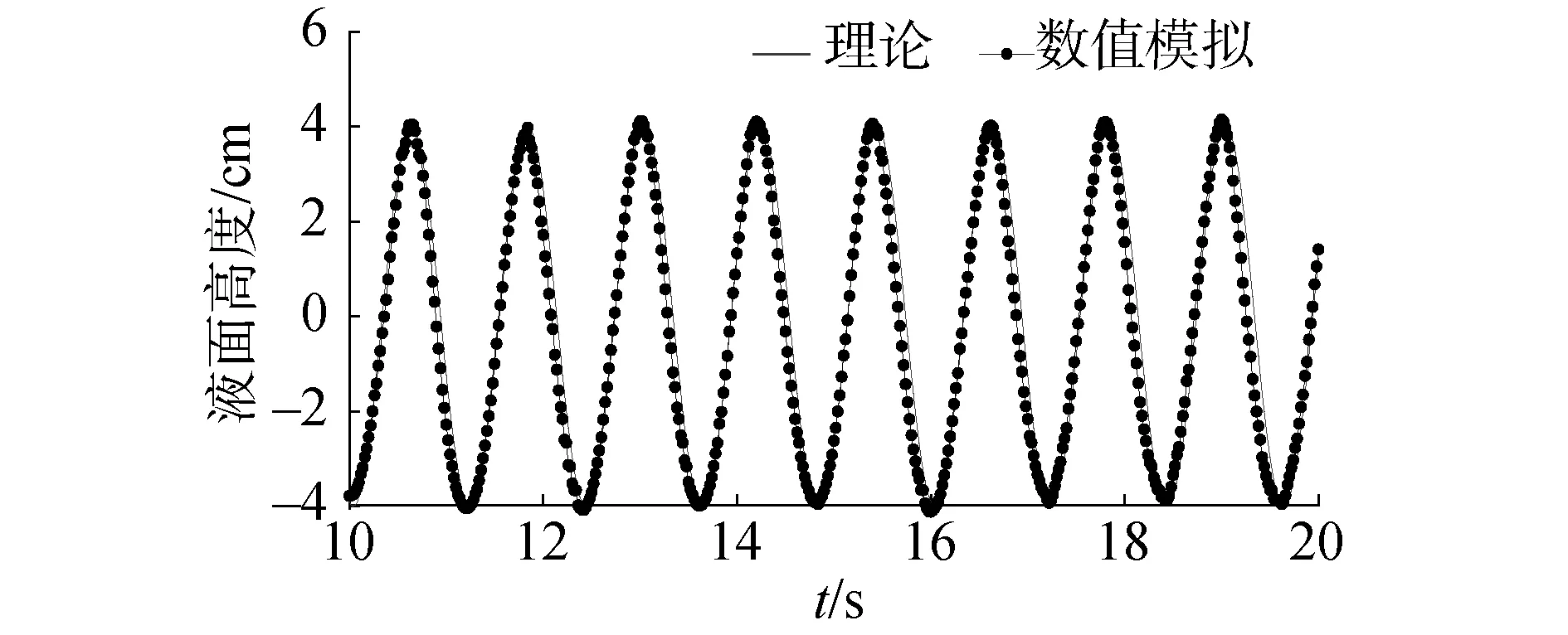
图4 波面历时曲线计算值与理论值比较Fig.4 Comparison between numerical and theoretical results of wave surface

为验证数值模型建立的准确性,在中国海洋大学工程水动力学实验室的波流水槽中,设计并进行了防淤积型透空式防波堤水动力特性的物理模型试验。依据重力相似准则,将防波堤的模型比尺定为1∶10进行试验,试验模型如图5所示。采用电容式波高仪进行波高数据采集。透空式防波堤的透射系数为:

图5 波浪与防波堤相互作用模型试验示意Fig.5 Model test diagram of interaction between wave and breakwater

Kt=Ht/H

(7)

式中:Ht为透射波高;H为入射波高。

比较水深h=0.4 m,波高H=0.08 m,周期T=1.0、1.2、1.4和1.6 s的4组工况的数模结果和物理模型试验透射系数,如图6所示。可以看出:在4组工况条件下,物理模型试验透射系数与数值模拟结果差距分别为8.1%、8.1%、5.6%和6.0%,因此可以认为建立的波浪与防波堤相互作用的模型是准确的。

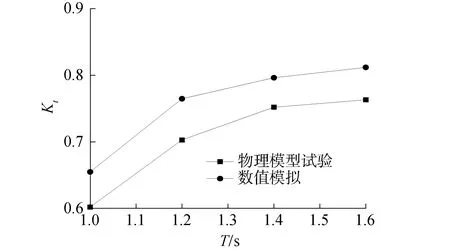
图6 物理模型试验透射系数和数值结果对比Fig.6 Comparison of transmission coefficients of physical model tests and numerical results

3 数值结果分析与讨论

建立模型时,在防淤积型透空式防波堤上拦沙板底面和前后表面布置多个压力测点,如图7(a)和图8(a)～(c)所示。假设测点处的压强可以代表该点周围面积压强的平均值,则该测点附近所承受的波浪力可以表示为测点压强与面积的乘积,方向垂直作用于受力表面,对上拦沙板各表面所受的波浪力进行矢量合成,得到作用在挡板上总的波浪压力F,并用ρgH3对其无量纲化,其中密度ρ取值1 000 kg/m3,重力加速度g取值9.81 m/s2。

图7 防波堤上拦沙板底面压力测点Fig.7 Pressure measuring point at the bottom of the upper board for sediment trapping on breakwater

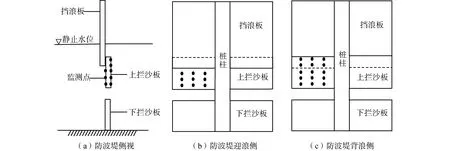
图8 防波堤上拦沙板侧面压力测点布置示意Fig.8 Schematic diagram of pressure measuring point arrangement on the side of the upper board for sediment trapping on breakwater

设定防淤积型透空式防波堤模型2个竖向支撑桩柱之间一段完整防波堤的宽度为40 cm,利用上拦沙板表面监测点压强计算挡板受力时,首先根据结构对称性选取上拦沙板各点的压强值,如图7(b)所示。

3.1 防波堤消波效果

防淤积型透空式防波堤透射系数随波陡的变化如图9所示,采用多项式回归方法对同一工况下数据点进行拟合,获得透射系数随波陡变化的二阶曲线。可以看出:透射系数随着波陡的增大而减小,且减小速率逐渐变大。上拦沙板下落距离D越大,即挡板的相对入水深度越大,透射系数越小,且随着下落距离的增大,透射系数的减小速率加快。挡板的初始入水深度为0.1 m,当上拦沙板下落0.05和0.10 m时,入水深度分别增大了50%和100%。经比较,在T=1.0 s时,上拦沙板下落距离D=0.05 m和D=0.10 m比D=0 m时波浪的透射系数最高分别减少28%和58%,在T=1.2 s时,波浪的透射系数最高分别减少15%和45%,在T=1.4 s时,波浪的透射系数最高分别减少9%和42%,在T=1.6 s时,波浪的透射系数最高分别减少11%和47%。

防淤积型透空式防波堤透射系数随H/gT2的变化如图10所示,可以看出:拟合的函数曲线可以较准确的预测新型透空式防波堤的透射系数。透射系数预测公式采用二阶多项式函数的形式,使公式透射系数的预测值与模拟结果之间的误差更小,可以更准确预测其他工况条件下防波堤的透射系数。

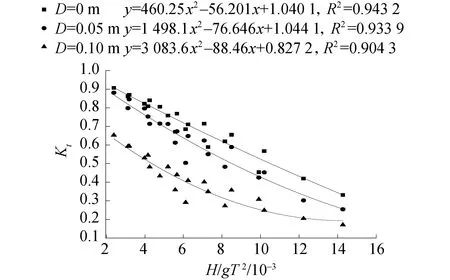
图10 透射系数随H/gT2变化关系Fig.10 Relation of transmission coefficient with H/gT2

不同水深条件,上拦沙板下落不同距离时,防淤积型透空式防波堤透射系数随周期的变化如图11所示,上拦沙板没有下落时,水深h由0.45 m降为0.4 m,防波堤透射系数增大,将上拦沙板的位置降低0.05 m后,透射系数有所减小,但仍大于水深h=0.45 m时,当上拦沙板降低0.10 m后,防波堤透射系数急剧减小,消波效果明显优于水深h=0.45 m时。由此可见,在防波堤所处位置水位变化较大时,可以通过降低上拦沙板使防波堤消波效果重新满足港池内的设计要求,当水位较高时将上拦沙板升起,使挡板开度大小充分满足水体交换所需的过流面积。

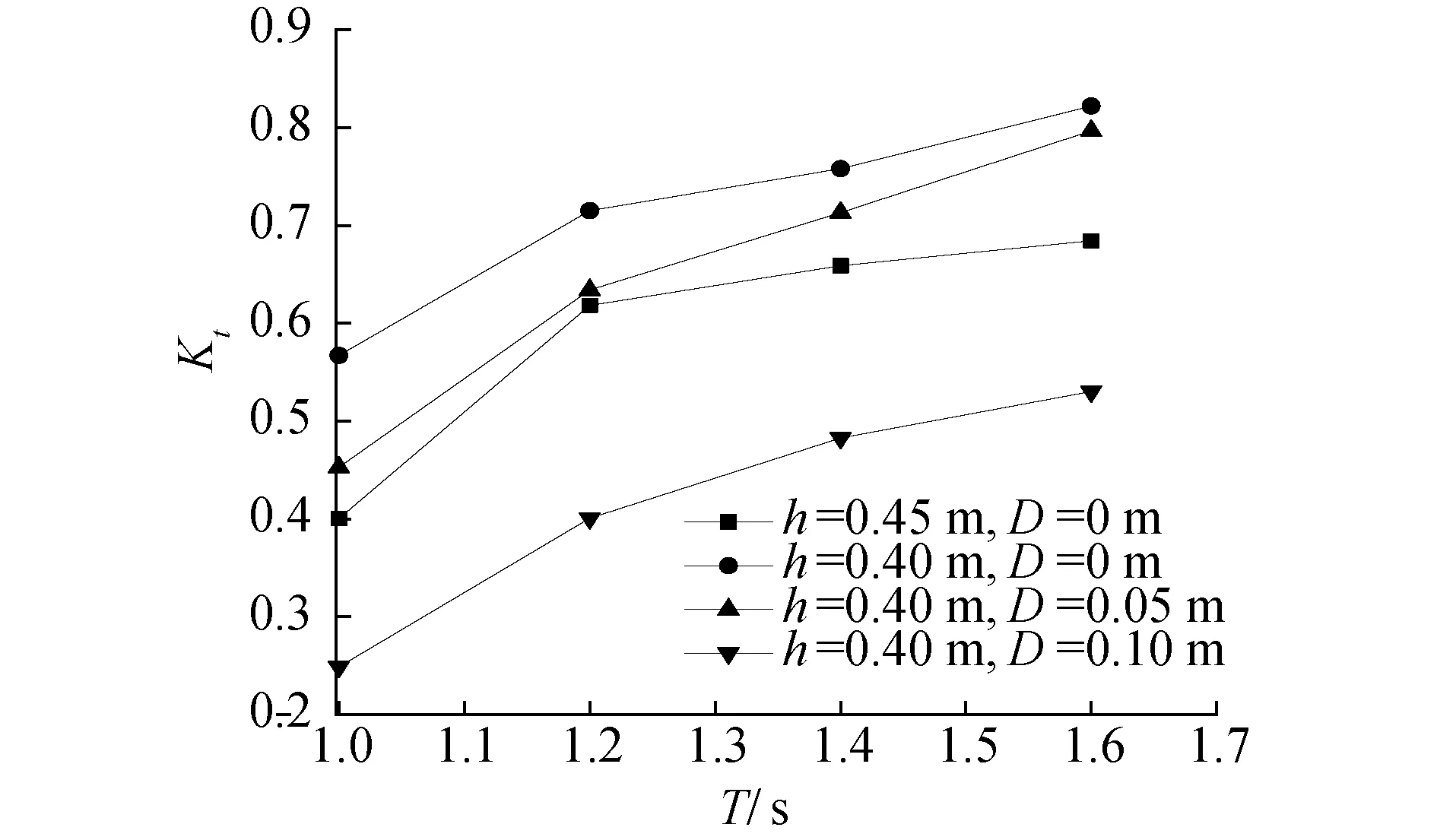
图11 透射系数随周期变化关系Fig.11 Relation of transmission coefficient with period

Koraim[26]研究了3种竖直挡板透空式防波堤的透射系数,在相对入水深度d/h=0.25和d/h=0.5时,3种模型与本文模型透射系数与周期的曲线关系如图12(a)和12(b)所示。由图12(a)可见4种结构形式的防波堤透射系数都随周期增大而增大,但3种传统透空式防波堤的透射系数随周期的增长的度更快,相同工况下,防淤积型透空式防波堤的透射系数小于3种传统透空式防波堤。由图12(b)可见,除了周期T在1.1～1.3 s时,其他工况下防淤积型透空式防波堤的透射系数小于以上3种透空式防波堤。还可看出,防淤积型透空式防波堤透射系数随周期增大趋于稳定,而3种传统透空式防波堤的透射系数随周期的增大持续增大,因此可以认为入射波浪的周期越大,采用防淤积型透空式防波堤进行消波的优势越明显。

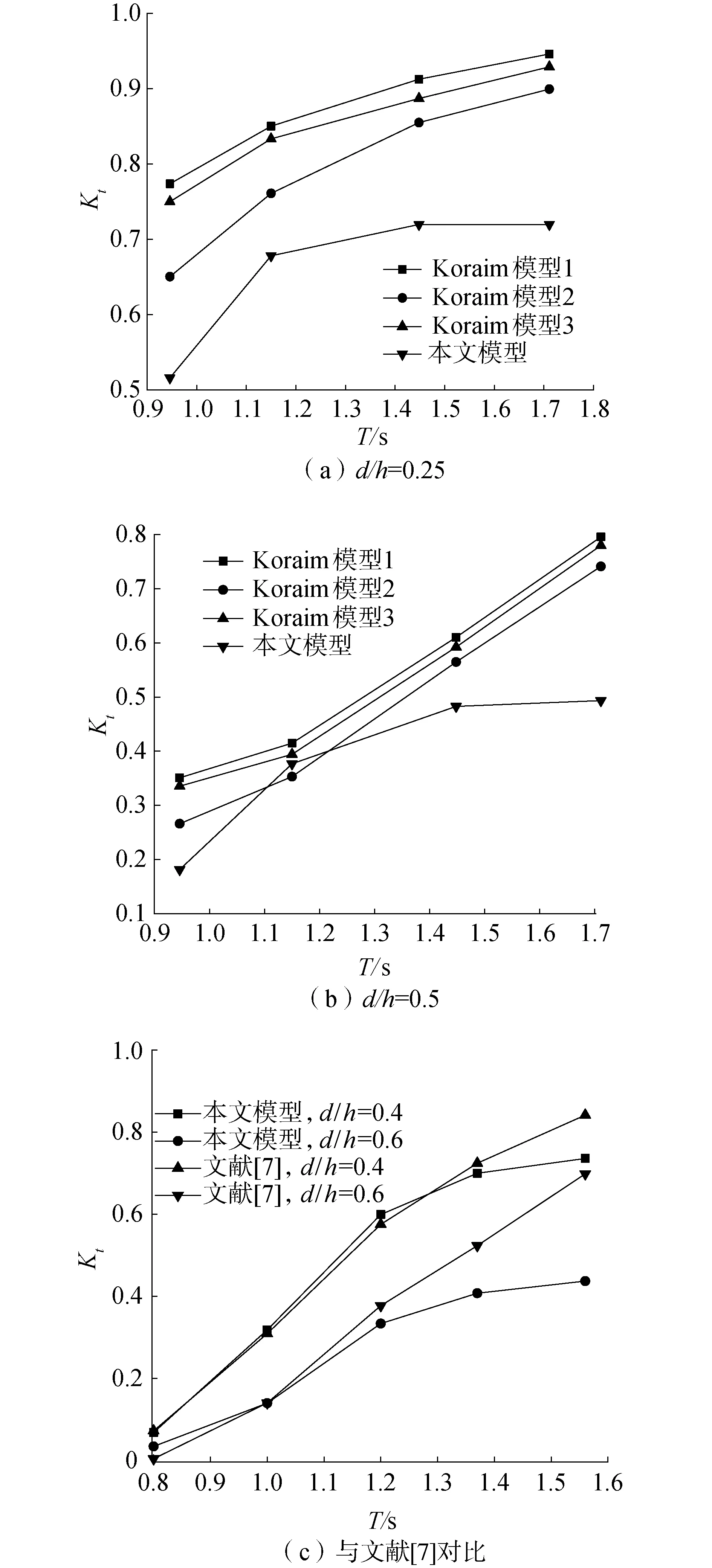
图12 本文防波堤和传统透空式防波堤透射系数比较Fig.12 Comparison of transmission coefficients between breakwater and traditional permeable breakwater in this paper

图12(c)给出相对入水深度d/h=0.4和d/h=0.6时,本文防波堤与琚烈红[7]研究的防波堤透射系数与周期的关系。可以看出,除个别工况外,防淤积型透空式防波堤的透射系数小于传统透空式防波堤的透射系数,并且防淤积型透空式防波堤透射系数随周期增大逐渐趋于稳定,而传统透空式防波堤的透射系数随周期增大而增大。因此可以认为在竖直挡板式防波堤基础上增加下拦沙板具有更好的消波效果,尤其在入射波浪周期较大时,这种优势更加明显。

3.2 防波堤上拦沙板水平波浪力

防淤积型透空式防波堤上拦沙板水平波浪力无量纲参数F/ρgH3随波陡H/L的变化如图13所示,可以看出:F/ρgH3随H/L增大而减小,但其减小速率逐渐变慢,最后趋于稳定。对比挡板位于3种不同位置时的波浪力曲线可以发现,在波陡较小时,上拦沙板下落距离D越大,水平波浪力也越大,但上拦沙板下落距离D=0.10 m的曲线纵坐标F/ρgH3下降速率更快,当波陡增大到一定数值后,上拦沙板下落距离D=0.10 m时的水平波浪力小于D=0.05 m时,甚至小于D=0 m时。这是由于上拦沙板下落后,挡板前侧面直接承受波浪荷载的面积增大,大波高波浪作用在上拦沙板前侧面的波浪力增大,挡板两侧压力差减小,故作用在上拦沙板的合力减小。

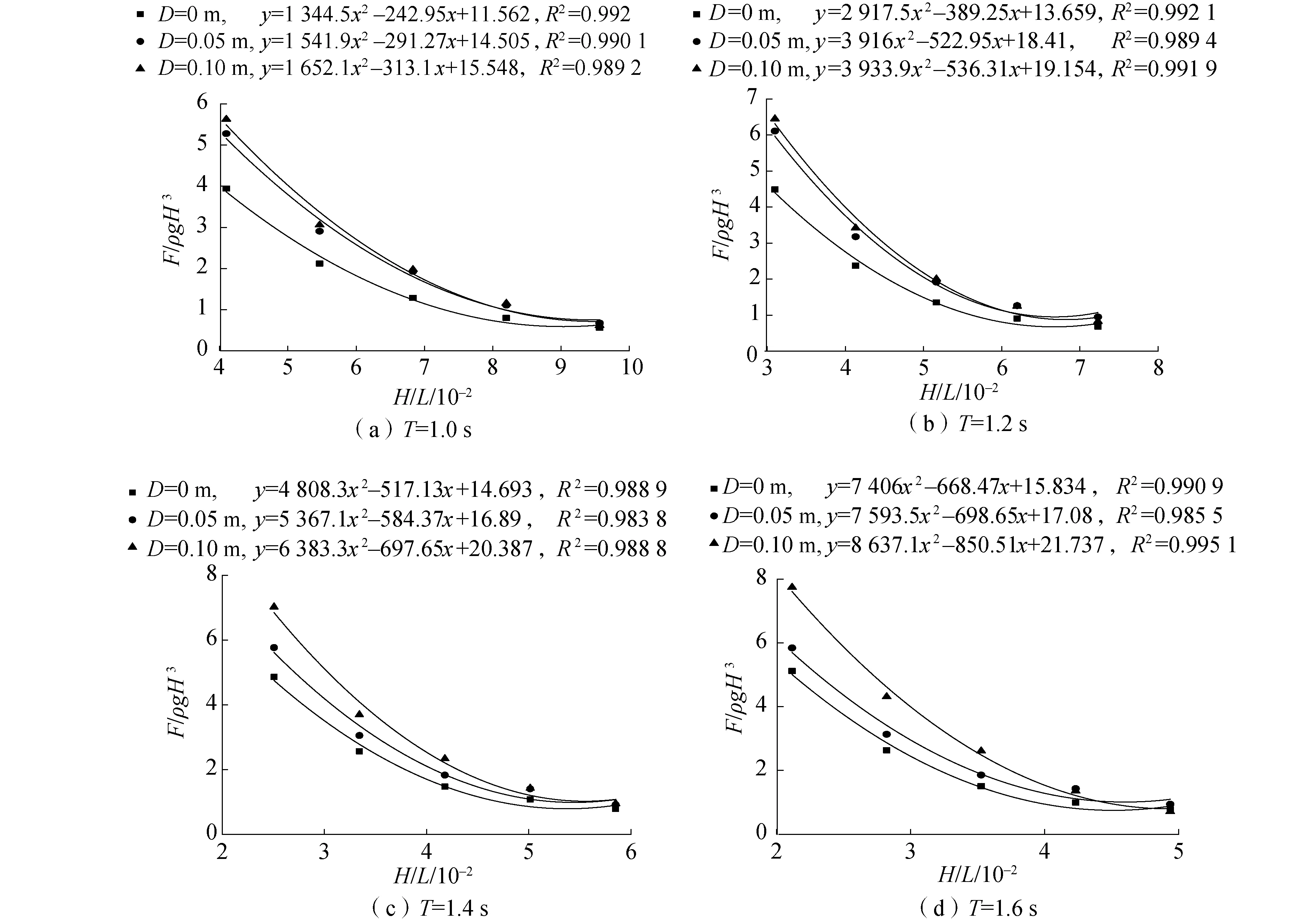
图13 水平波浪力无量纲参数F/ρgH3随波陡变化关系Fig.13 Relationship between dimensionless number of horizontal wave force F/ρgH3 and wave steepness

3.3 防波堤上拦沙板底面上托力

防淤积型透空式防波堤上拦沙板底面上托力无量纲参数F/ρgH3随波陡H/L的变化如图14所示,可以看出:F/ρgH3随H/L的增大持续减小,但F/ρgH3减小速率逐渐变慢,趋于稳定后曲线末端略有提升。从数据点的分布来看,压力数值在持续减小,因此曲线末端的提升应与二阶函数的拟合形式有关。模拟过程中上拦沙板处于完全静止状态,从各曲线图可以得出,上拦沙板下落距离D越大,上托力逐渐变大。随着水深增加,波浪的静水压力部分增大,而动水压力减小。挡板底面压力主要受静水压强的影响,上拦沙板底面位于水下位置越深时,静水压强的影响越大,底面上托力也越大。

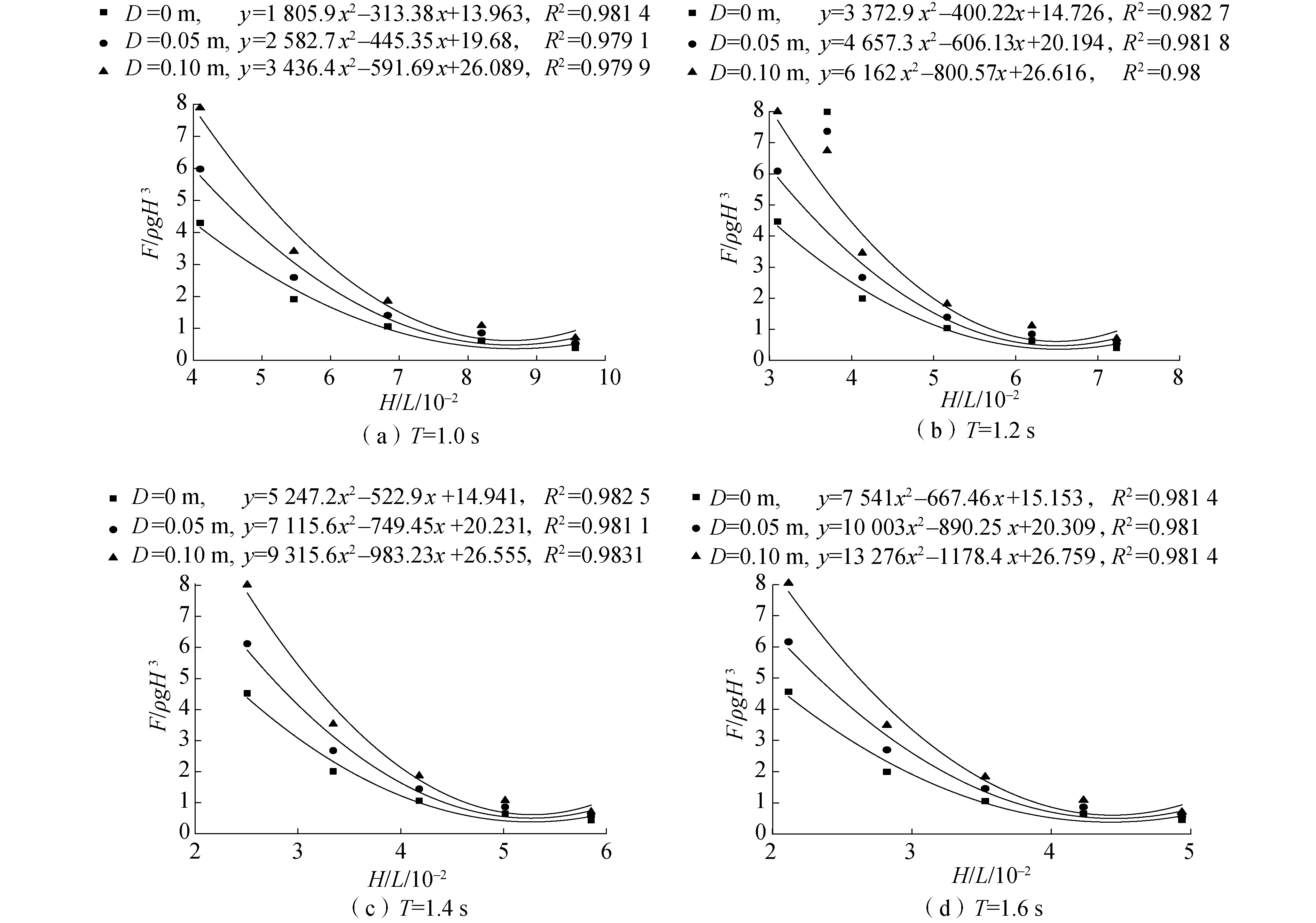
图14 底面上托力无量纲参数F/ρgH3随波陡变化关系Fig.14 Relationship between dimensionless number of the upper support force F/ρgH3 and wave steepness

4 结论

1)防淤积型透空式防波堤的透射系数随着波陡H/L的增大而减小,具有较好的消波效果,且更适用于波浪周期较大的海域。

2)工作海域水位降低时,新型透空式防波堤透射系数增大,可以通过降落上拦沙板降低透射系数,挡板入水深度增大50%时,透射系数减小9%～28%,入水深度增大100%,透射系数减小了42%～58%,可使防波堤的消波效果满足设计需求。

3)上拦沙板水平波浪力的无量纲参数F/ρgH3随波陡H/L的增大而减小,在波陡较小时,上拦沙板下落距离D越大波浪力也越大。

4)上拦沙板底面上托力的无量纲参数F/ρgH3随着波陡H/L的增大而减小,上托力主要受静水压强的影响,上拦沙板下落距离D越大,挡板所受上托力越大。