导叶翼型优化对水泵水轮机“S”特性的影响
李琪飞, 黄腾, 郑非, 辛路, 谢耕达
(1.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050; 2.甘肃省流体机械及系统重点实验室,甘肃 兰州 730050)
水泵水轮机在“S”特性区会出现转速对应多个流量的非设计工况,因而机组在“S”特性区内的运行非常不稳定[1-3]。机组启动阶段,多种工况之间的瞬态变化可能导致机组并网时间变长甚至并网失败;机组甩负荷后,由于引水管道内依然存在大量的水,会引起转轮高速旋转,并使机组进入反水泵工况[4-6];当机组在“S”特性显著的工况下运行时会导致机组无叶区强烈的压力脉动,引起机组发生强烈震动[7-9]。水泵水轮机在“S”特性区运转极其不稳定,转速值对应多个流量值有可能使得机组在多个工况间频繁转变,这种情况会导致机组运转严重失稳[10-13];预开导叶可以改善水泵水轮机进入不稳定的“S”区,但是有可能增大机组无叶区压力脉动值,从而影响水泵水轮机机组安全稳定运行[14-16]。
本文采用SSTk-ω湍流模型,以国内某型抽水蓄能电站水泵水轮机为研究对象,通过优化活动导叶翼型改善水泵水轮机 “S”特性以及无叶区压力脉动。
1 设计流程及模型建立
1.1 活动导叶设计流程
由于水泵水轮机的导水机构为圆柱形导水机构,因此可以通过改变活动导叶的翼型型线对现有的活动导叶改型。本文参考水轮机优秀水力设计模型、水轮机设计手册导叶叶型断面尺寸表以及原有翼型设计数据对活动导叶翼型进行改型,在保持原有导叶弦长不变的情况下设计出新的活动导叶。通过改变活动导叶翼型改变入水方向与速度从而改善水泵水轮机机组“S”特性。改型前后导叶翼型如图1所示。
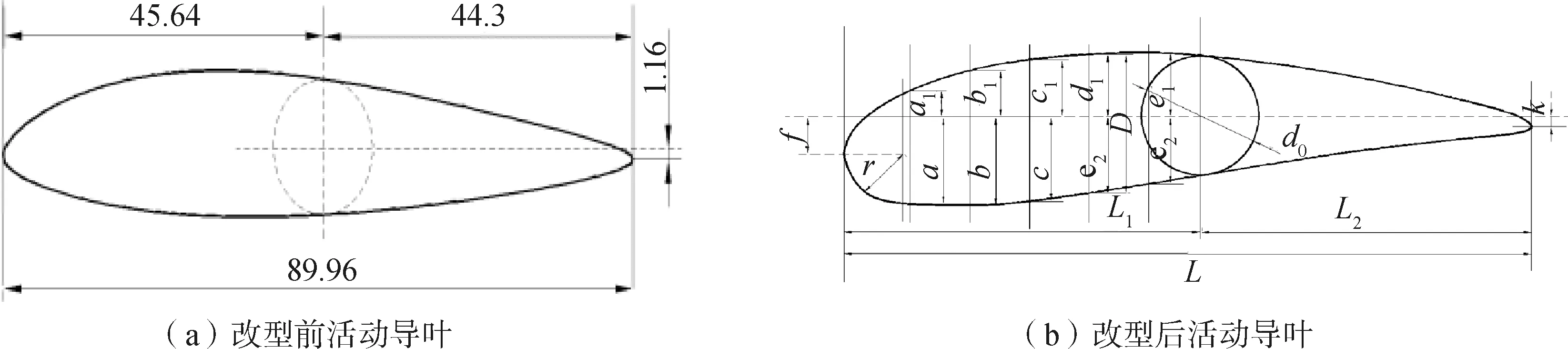
注:D0为638.619 mm,a为11.036 mm,a1为2.85 mm,b为11.247 mm,b1为5.011 mm,c为11.145 mm,c1为6.903 mm,d为10.273 mm,d1为7.714 mm,L1为47.385 mm,e为9.272 mm,e1为8.238 mm,d0为16.099 mm,m为7.468 mm,m1为5.891 mm,k为0.912 mm,f为4.722 mm,r为6.016 mm,L为89.897 mm,L2为42.611 mm图1 改型前后导叶翼型示意Fig.1 Schematic diagram of the modified anterior and posterior guide vane airfoils
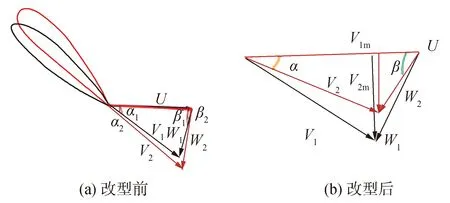
图2 改型前后导叶翼型速度三角形对比及叶片进口速度三角形Fig.2 Comparison of the front and rear guide vane airfoil velocity triangles of the modification
1.2 网格划分及模型建立
本文研究对象为水泵水轮机模型,过流部件由蜗壳、固定导叶、活动导叶、转轮和尾水管组成,示意如图3所示,具体参数如表1所示。

表1 模型水泵水轮机几何参数Table 1 Geometric parameters of model pump turbine
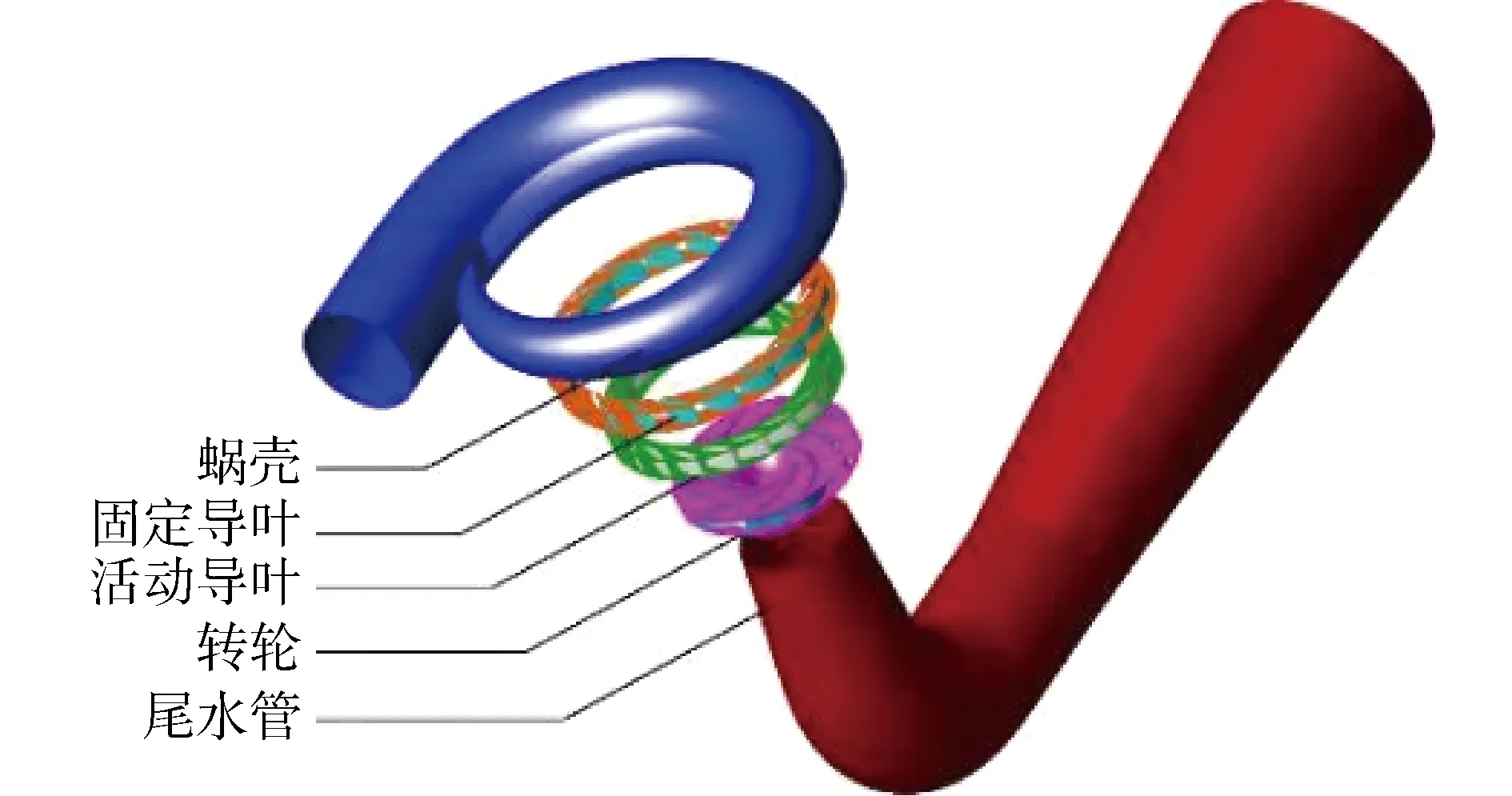
图3 模型水泵水轮机计算区域Fig.3 Model pump turbine calculation area
为了保证数值计算结果可行可靠,本文网格划分采用商业软件ANSYS的子功能ICEM进行全流道六面体网格划分。经过网格无关性验证,最终采用网格质量为0.3左右,网格总数为610万左右的网格进行计算。网格划分结果如图4所示。
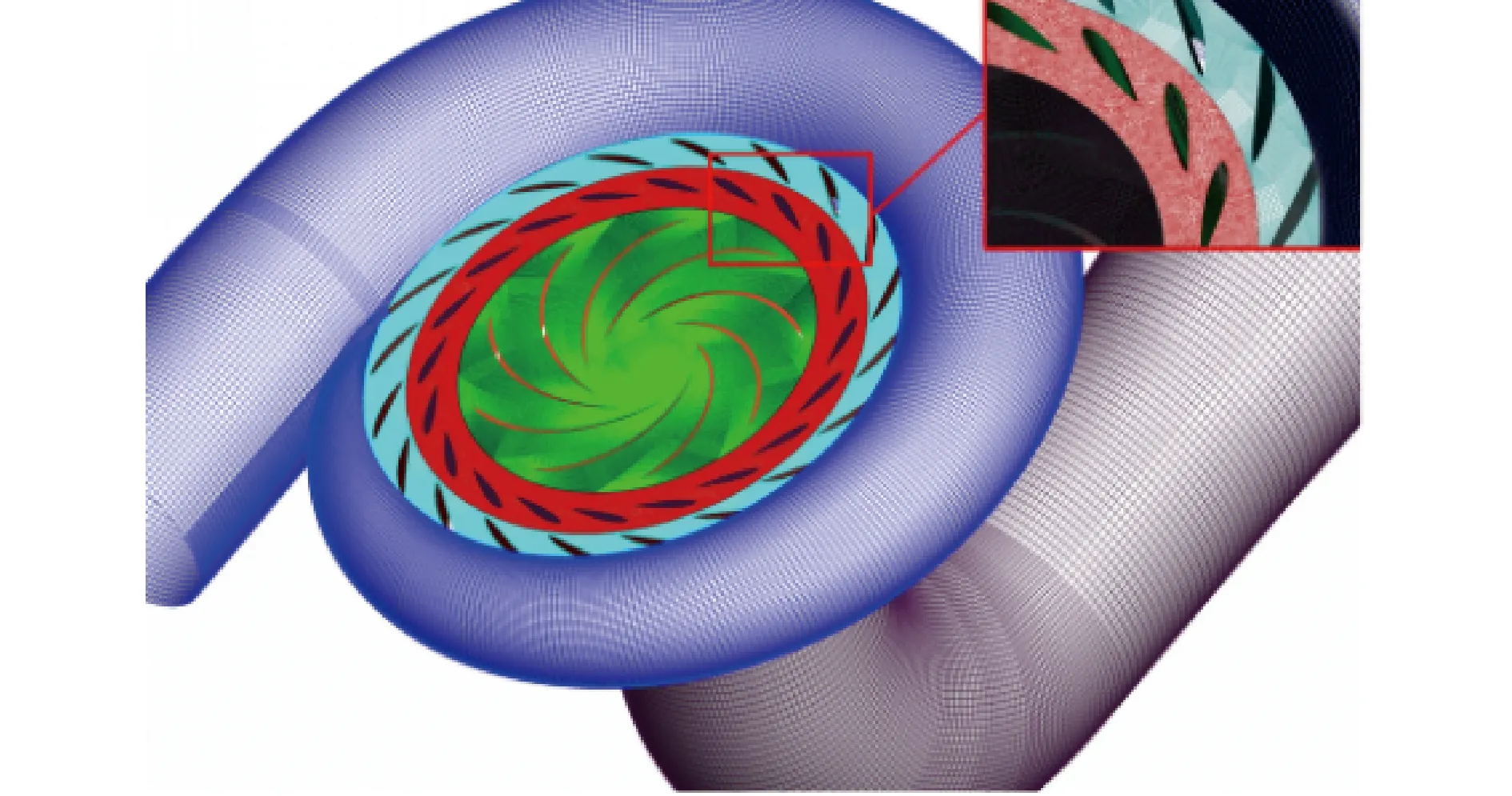
图4 局部网格示意Fig.4 Local grid diagram
2 试验台简介及数值计算方法
为了验证湍流模型的可靠性以及建模与数值计算的可行性,本文拟将数值计算结果与实验结果进行对比。试验台示意如图5所示。本文模型试验采用H=30 m恒定水头对模型机进行试验,利用转矩仪以及流量计测出转轮转速以及流量并与计算结果进行对比。
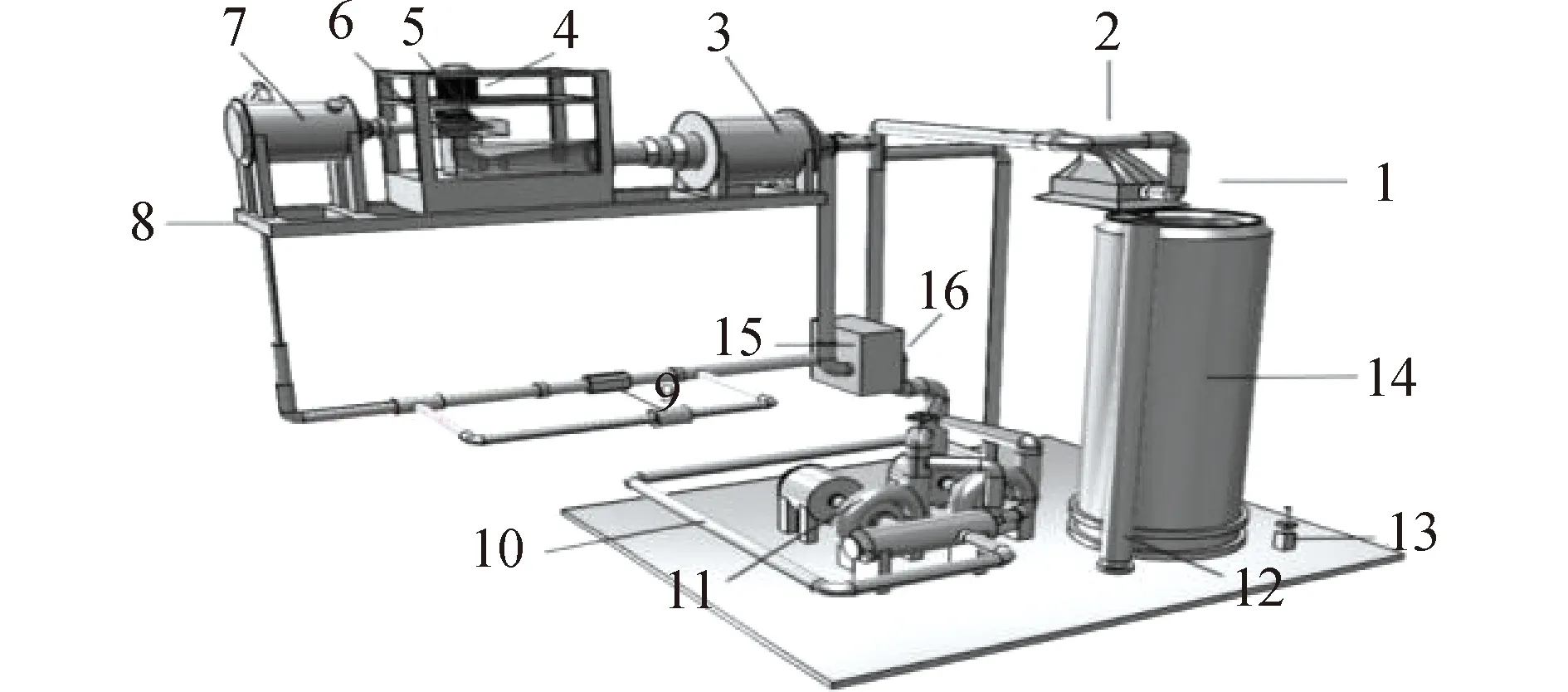
注:1.偏流器,2.喷嘴,3.低压箱,4.测功电机,5.扭矩测量系统,6.水泵水轮机7.高压箱,8.支架,9.流量计,10.封闭系统回路管,11.水泵12.敞开系统回水管,13.称重传感器,14.称筒15.水冷系统,16.换向管路图5 水泵水轮机试验平台Fig.5 Water pump turbine test platform
由于SSTk-ω湍流模型可以有效捕捉近壁面的流动,尤其是对水泵水轮机这种多导叶、多叶片的复杂几何模型有较强的准确性以及适应性,因此本文选取SSTk-ω湍流模型开展数值模拟。流体介质设为常温水,壁面采用无滑移壁面边界条件;进口和出口分别设置为质量流量进口和自由出流;静止域与旋转域之间的数据传递依靠INTERFACE边界条件。采用SIMPLE C速度压力耦合算法,残差值设置为10-6,时间步长设置为0.000 467 3 s。
3 计算结果及分析
3.1 可靠性验证
本文研究选取模型水泵水轮机活动导叶a0=33 mm进行数值计算可靠性验证。选取7个工况点对其进行定常数值计算。将数值计算的结果进行单位转速n11、单位流量Q11的转换分别为:
(1)
(2)
通过换算所得Q11和n11,绘制出n11-Q11特性曲线。利用换算所得n11-Q11特性曲线与试验曲线进行对比,其结果如图6所示。通过对比,两者具有很高的吻合度,误差值保持在6%以内,满足工程研究要求。因此,本文数值计算所选用的模型具有较高的可靠性。

图6 实验与模拟结果对比Fig.6 Comparison of experimental and simulation results
3.2 特性曲线分析
根据前文的换算结果,对原有导水机构导叶替换为优化后的翼型导叶模型水泵水轮机进行数值模拟,分别得到数据。并绘制出n11-Q11曲线,如图7所示。
从图7的试验曲线可以看出,在导水机构导叶为原有翼型的情况下出现了很明显的“S”特性区。由于“S”特性的存在导致机组在运行的过程中及其的不稳定。将原有导水机构中的导叶替换为优化翼型的导叶后,机组“S”特性得到了一定的改善。因此,通过优化导叶翼型来改善水泵水轮机“S”特性可行。
3.3 S1流面流态分析
为了更好展现出水泵水轮机流场特性,本文选取转轮部位S1流面作为进一步分析的研究对象。将转轮上冠下环的等距面选取作为S1流面。利用后处理软件CFD-Post做出S1流面的速度流线分布图,如图8所示。
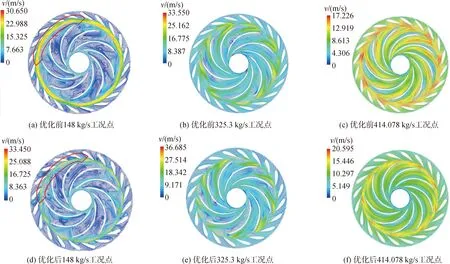
图8 不同工况下S1流面流线图Fig.8 Streamline diagram of S1 stream surface under different working conditions
由图8可以看出,147.9 kg/s流量工况下,不管活动导叶翼型优化与否,在无叶区均出现了较明显的高速水环,但是将活动导叶翼型优化后,无叶区的高速水环相较优化前有了一定的削弱,从转轮区域的叶道流场分析,147.9 kg/s流量工况下,装配原有活动导水机构机组的叶道内分布了大量的涡,且基本集中在距转轮入口处,然而优化活动导叶翼型后,转轮区域流态较优化前有了较好的改善,部分叶道内未出现明显的旋涡流动。从325.3 kg/s以及414.078 kg/s的2个工况点的流面看,优化活动导叶翼型前后流态相似,并且在活动导叶及转轮流域内均未出现明显的旋涡。
根据以上分析,优化活动导叶翼型后,由于翼型骨线相较优化前发生了变化,活动导叶区域出流角也随之改变,从而使得无叶区高速水环在一定程度上被破坏,进而改善了转轮入流量,这也是导致机组“S”特性得到一定改善的其中一个原因。
3.4 机组效率计算
为了研究采用优化翼型活动导叶的机组的效率,以导叶开度a0=33 mm工况下模型水泵水轮机为研究对象,以选用优化活动导叶翼型后的水泵水轮机为模型,在流量特性曲线上选取Q1=750 kg/s,Q2=650 kg/s,Q3=530 kg/s,Q4=300 kg/s共4个工况点进行数值计算,计算出机组效率,如图9所示。
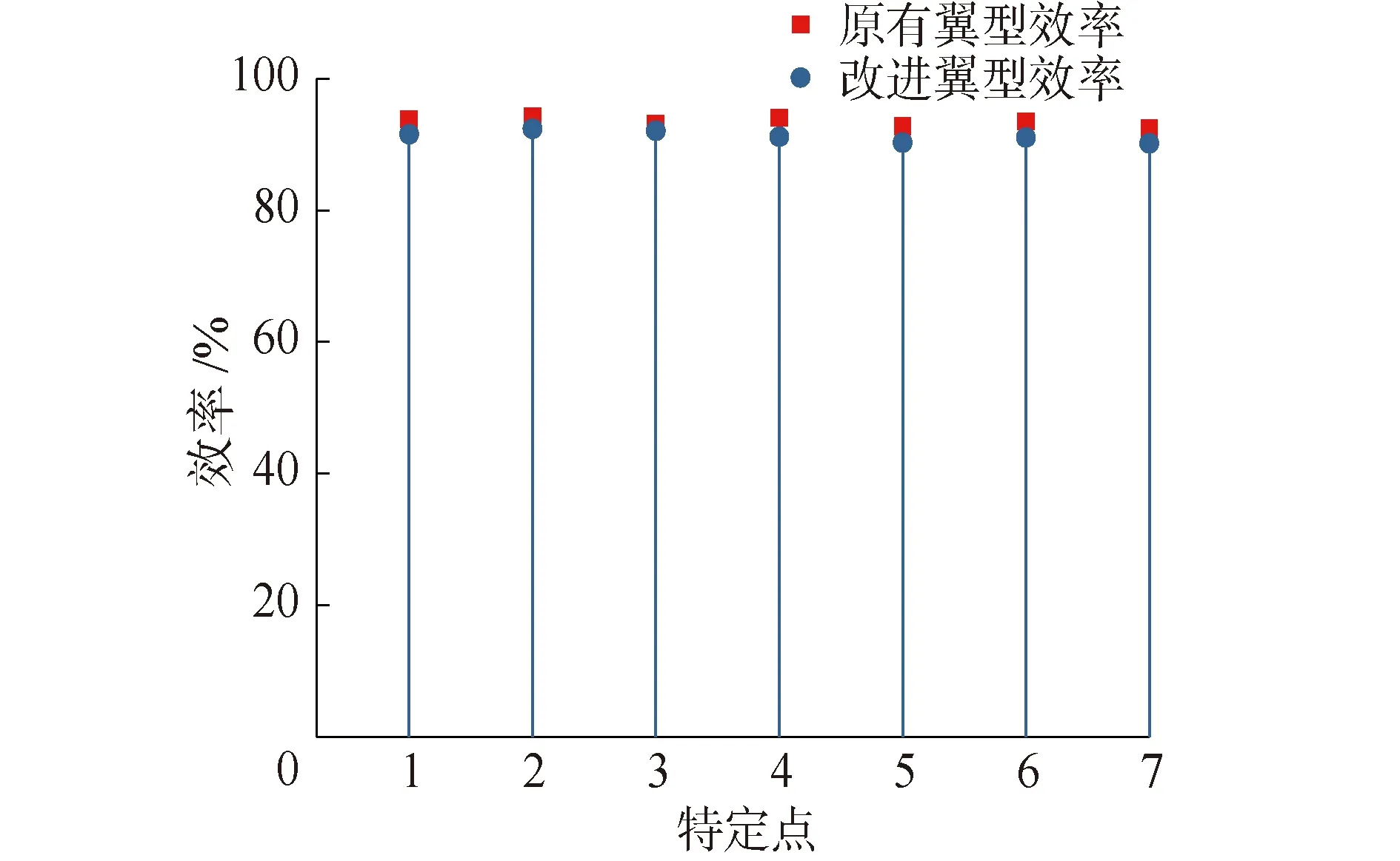
图9 机组各工况点效率Fig.9 The efficiency of the unit operating point
由图9可以看出,将活动导叶翼型优化后,机组效率出现了微小幅度的下降,但针对可逆式机组小流量工况的过渡过程,其效率的微小幅度下降是在可允许范围内的。而且,在机组效率为小幅度下降的前提下,对机组“S”特性的改善应该占据主导地位,以保证机组在小流量工况下的稳定运行。显然优化活动导叶翼型对改善机组“S”特性取得了较好的效果。因而本文活动导叶翼型的优化是有效的。
3.5 S1流面湍动能分析
由于将原有活动导叶全部替换为优化翼型导叶之后,机组整体效率出现了微小幅度下降。而转轮又是机组主要的能量转化过流部件,因此分析转轮部位S1流面湍动能分布是有必要的。
由图10可以看出,湍动能区域出现在无叶区附近影响了叶片进口来流,最大湍动能值为32.44 kg/J。改型后最大湍动能值增大为44.24 kg/J,均集中在无叶区,但无叶区附近的湍动能区域面积有所减小但其强度变高,整体出现了一些能量耗散较大的区域,比较Q4工况,改型前后湍动能分布区域较为相似,均出现无叶区附近,只是改型后环形无叶区的湍动能面积相应减小,活动导叶出口区域能量损失降低,从整体来看,将活动导叶翼型优化后,无叶区以及转轮区域均出现了一定的能量耗散,导致机组整体效率出现了微小幅度的下降。而造成能量损失主要的原因有:1)活动导叶和转轮叶片之间产生了动静干涉效应,导致无叶区出现了能量耗散;2)优化翼型后的活动导叶附着流动不佳,在靠近导叶进口端就出现了流动剥离,从而使得在活动导叶区域就出现了大量的涡,且由于迟滞效应这些涡会一直存在到转轮区域才会逐渐消散;3)进口流量与转轮转速的匹配对湍动能会产生较大影响,从而造成一定的能量损失。这些原因共同导致了机组效率出现微小幅度下降。

图10 不同工况点下S1流面的湍动能分布Fig.10 Turbulent kinetic energy distribution of the flow surface S1 at different operating points
3.6 无叶区压力脉动频域分析
水泵水轮机的运行过程中不稳定性主要来源于机组内部水力振动,而机组的水力振动又主要来自于无叶区的压力脉动[17]。
为了合理的解释无叶区压力脉动,引入无量纲参数ΔH/H表示压力脉动的程度为:
(3)
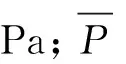
为了细致地了解到导叶翼型的优化对附近流域的影响,在无叶区选取了4个监测点P1~P4,进行无叶区压力检测,如图11所示。

图11 压力监测点示意Fig.11 Schematic diagram of pressure monitoring points
图12展示了转轮区叶片区域内各监测点在水轮机的压力脉动时域图与频域瀑布图。此工况虽然压力脉动复杂但依旧存在周期性的波动变化,改型后的压力波动260 kPa附近波动且相比原型波动幅度降低。频域图可以看出在监测得时间点内可以看出压力脉动多以低频率为主。整体频率成分相对简单,第1主频受到动静干涉影响降低从而更加接近其叶片转动频率。

图12 P1与P3时域图与频域图Fig.12 P1 and P3 time domain plots and frequency domain plots
因为来流在进入转轮流道时与转轮叶片工作面发生冲击并产生了冲击分流,这些冲击分流使得无叶区出现了不稳定的压力脉动;另一方面,由转轮和活动导叶组成的动静叶栅干扰也是无叶区出现压力脉动的一个主要原因,转轮不断扫过由流体流经活动导叶组成的静叶栅所形成的尾迹,并且不断击打着这些尾迹,从而使得无叶区出现了脉动幅值周期性变化的压力脉动。改型后,无叶区内单位时间内涌入了更多的无撞击的有效水流,不仅最大程度上破坏了无叶区的高速水环,也减少了对转轮区域的直接冲击作用,压力幅值均有所下降,对于水泵水轮机这种经常变工况运行的水力机械来说存在一定是益处的。
4 结论
1)优化翼型后的活动导叶对无叶区高速水环造成一定的破坏,使得转轮叶道部位入流状况得到一定程度改善,从而对机组“S”特性起到一定的改善作用。
2)在活动导叶转动角度不变的条件下,优化导叶翼型后,入流角增大,来流液体与转轮叶片冲角减小,使得有效过流面积增大。这是改善内流特性的根本原因。
3)水泵水轮机的振动主要来自于无叶区压力脉动,受动静干涉的影响,无叶区振动会引起转轮叶片疲劳损坏。优化后,压力脉动振幅出现不同程度的下降,水流自导叶出口到叶片尾端,压力脉动强度分布稳定,脉动频域成分简化,提升了水泵水轮机的平稳运行能力。
——“AABC”和“无X无X”式词语

