GNSS-PPP多系统多频点组合定位精度分析

薛二锋，吕登申，赵廷宝

GNSS-PPP多系统多频点组合定位精度分析

薛二锋，吕登申，赵廷宝

（青海地理信息产业发展有限公司，西宁 810001）

为了进一步推广全球卫星导航系统（GNSS）精密单点定位（PPP）技术并实现多GNSS-PPP工程应用，基于国际GNSS服务组织（IGS）多模GNSS实验跟踪网（MGEX）测站数据，研究GNSS-PPP组合定位的精度以及性能：介绍和分析4大GNSS综合PPP技术；并采用多系统多频点组合定位测试PPP的收敛时间和定位精度，同时针对不同高度截止角对比分析单GPS-PPP与多GNSS-PPP效果。结果表明：多系统组合定位比单GNSS系统在精度以及收敛时间上都有显著改善，东、北、高3个分量的精度可平均提升30.7%，收敛时间可降低55.3%；由于多系统组合定位增加了可见卫星数，因此截止高度角对GNSS-PPP结果影响较小。

全球卫星导航系统（GNSS）；精密单点定位（PPP）；组合定位；收敛时间；高度截止角

0 引言

全球卫星导航系统（global navigation satellite system，GNSS）能够提供绝对位置坐标的空间技术，是现代社会数字经济最重要的基础，因此多数国家都在发展自己的GNSS系统。随着2020年中国北斗卫星导航系统（BeiDou navigation satellite system，BDS）全球组网，以及欧盟伽利略系统（Galileo）不断完善，加上美国全球定位系统（global positioning system，GPS）、俄罗斯格洛纳斯卫星导航系统（GLONASS），全世界已有4个完整的独立运营的GNSS、众多的区域增强系统（印度区域卫星导航系统（Indian regional navigation satellite system，IRNSS）、日本的准天顶卫星导航系统（quasi-zenith satellite system，QZSS）等），使得在轨卫星数已超过100颗，可用于导航的信号也超过30个频点；同时，世界上多家GNSS机构发布的产品（轨道、钟差、码间偏差（d，DCB）等）精度逐步提高，也促进了算法的不断迭代与改进。精密单点定位（precise point positioning，PPP）技术向着多系统多频点的组合定位方向发展。

常见的GNSS定位技术有差分定位和单点定位。载波相位动态定位（real-time kinematic，RTK）技术已非常成熟，广泛应用于各类工程项目。然而，RTK技术以及延伸的连续运行参考站（continuously operating reference stations，CORS）系统需要在地面均匀建设基准站，大范围的应用造成建设和运营成本巨大。相比而言，精密单点定位（precise point positioning，PPP）不依赖地面增强站，只需要单台接收机就能完成定位；以往PPP技术存在明显缺点（如收敛时间长、算法不成熟等），限制了实际应用。随着GNSS观测数据不断增多，近些年GNSS-PPP重新成为研究热点，采用模糊度固定技术（ambiguity resolution，AR）缩短PPP收敛时间[1-8]；另一些研究[9-13]采用多系统组合定位，有效地改善定位精度和收敛时间。将RTK技术引入PPP中是当前新的研究方向，PPP-RTK技术是通过地基增强系统处理将GNSS各类误差在“状态域”建模（state-space-modelling，SSM），采用非差PPP实现与RTK相当的定位效果。表1、表2比较了常见的GNSS技术[14]。表1、表2中：OSR（observation space representation）为观测空间表达；SSR（state-space-representation）为状态空间表达；VRS（virtual reference station）为虚拟参考站技术；MAC（master auxiliary concept）为主辅站技术；FKP（Flächen-Korrektur-Parameter）为区域改正技术；CQ2（cenmeter accuracy in quarters of hours using 2 frequencies）为使用2个频率在(1/4)h内实现厘米精度；DS1（decimeter accuracy in seconds using 1 frequency）为使用1个频率实现秒级分米精度；CS2（cenmeter accuracy in seconds using 2 frequencies）为使用2个频率以秒为单位的厘米精度；Phase-PPP为载波相位精密单点定位；Code-PPP为测距伪距码精密单点定位。

表1 OSR-CS2技术的技术参数

表2 SSR技术的技术参数

本文研究4大GNSS综合PPP技术，采用多系统多频点组合定位测试PPP的收敛时间和定位精度，同时针对不同高度截止角对比分析单GPS-PPP与多GNSS-PPP效果，旨在为进一步推广PPP技术并实现多GNSS-PPP工程应用提供参考。

1 GNSS PPP模型与数据处理方法

PPP是一种利用单台GNSS接收机采集伪距码（code）和相位（phase）观测数据，并结合GNSS精密星历和精密钟差，采用非差算法模型获得精密坐标的方法。由于非差算法模型无法消除硬件延迟以及初始相位偏差，导致PPP无法获得模糊度固定解，并由于伪距噪声影响以及卫星的空间几何变化缓慢，会造成如表2所示的相位-PPP收敛时间较长的结果，精度也只有分米级别。

随着4个GNSS的发展，卫星数量和频点不断增多，有如表3所示的各星座的频点标识码（identity document，ID）分配和系统简码的关系[15]。其中：BDS-3及北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite（regional）system，BDS-2）的简称为“C”、GPS的简称为“G”、GLONASS的简称为“R”，以及Galileo的简称为“E”。

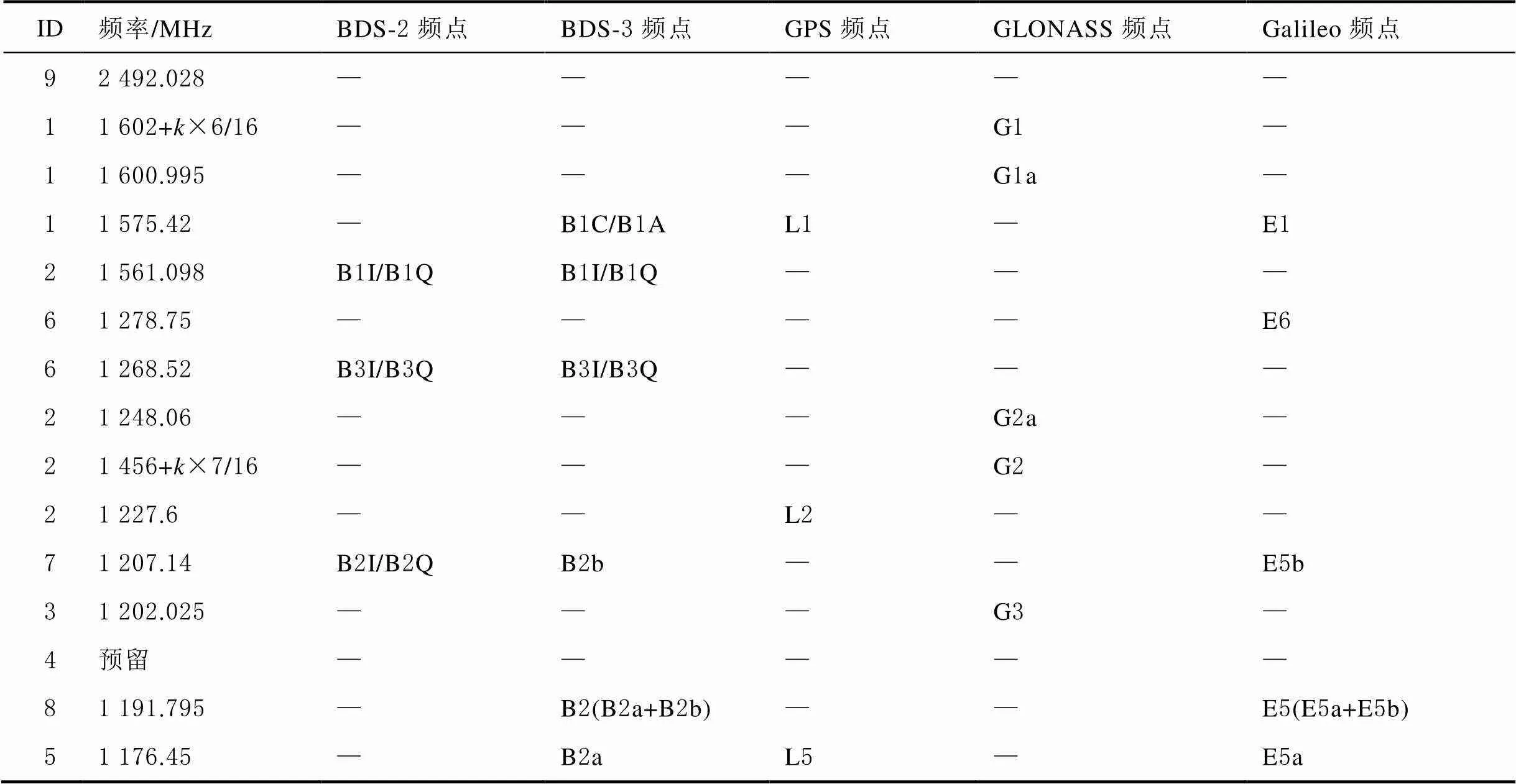
表3 国际导航卫星频点ID分配

采用多系统多频点联合算法[5-9]处理的计算公式为

本文选择国际GNSS服务组织多模GNSS实验跟踪网（International GNSS Service-multi GNSS experiment，IGS-MGEX）不同大洲地区的核心站点（站点信息如表4所示），在2021-05-05—2021-05-12的观测值进行GNSS-PPP实验，采用德国地学研究中心（Geo Forschungs Zentrum，GFZ）提供的GNSS精密星历和精密钟差产品。表5列举了PPP计算采用的算法策略。

表4 测站信息统计

表5 PPP解算处理策略

2 实验与结果分析

GNSS-PPP实验采用5个站2021年年积日第125—132天连续7 d的观测值进行动态解算。图1显示了观测数据中的卫星跟踪情况，图1（a）～图1（d）分别表示GPS、GLONASS、BDS和Galileo卫星数以及高度截止角。BDS卫星包含静止地球轨道卫星（geostationary Earth orbit，GEO）、倾斜地球同步轨道卫星（inclined geosynchronous orbit，IGSO）和中圆地球轨道卫星（medium Earth orbit，MEO），GEO的高度角均大于30°且全天可见，IGSO卫星星空图呈现“8”形状[16-17]。

图1 MGEX-JFNG站2021年年积日第125天空视图

PPP解算采用不同导航卫星系统组合，分别进行6组实验：单GPS系统、单BDS系统、单GLONASS系统、GPS/GLONASS双系统组合、GPS/GLONASS/BDS三系统组合、GPS/GLONASS/ BDS/Galilen四系统组合（对应图2中图例显示G、C、R、G/R、G/R/C、G/R/C/E）；图2显示了多系统PPP计算实验结果。图中从上至下分别表示东（E）、北（N）、高（U）3个坐标分量、可见卫星数和几何精度因子（geometric dilution of precision，GDOP）值。从图中结果可见：多系统PPP解算收敛时间明显比单系统快，且每个历元可用卫星数达到25颗，是单系统的2倍多；4个系统（G/R/C/R）组合的PPP解算GDOP值在1上下小范围波动，体现出解算星座整体网型空间分布合理的特性。值得注意的是，BDS单系统的GDOP值也非常小，这是因为BDS有3种卫星轨道[18]，比其他3个系统只有单一轨道有更好的空间几何分布。

从图2实验结果可以明显看出，多系统较单系统的收敛时间明显加快。更进一步对选取的5个不同大洲的MGEX测站2021年年积日第346—359天的数据采用GNSS-PPP和GPS-PPP处理（如图3所示），统计发现多系统GNSS-PPP平均收敛时间10 min左右，而单GPS-PPP平均收敛时间30 min左右，收敛时间降低55.3%。统计连续多天GNSS-PPP数据解算的坐标精度，采用IGS官网公布的JFNG站IRTF2014坐标作为真值，利用均方根误差（root mean square，RMS）作为指标。解算结果为：单GPS-PPP在坐标三分量E、N、U上的平均RMS分别为1.25、0.96、3.52 cm；而多系统GNSS-PPP的E、N、U平均RMS分别为0.81、0.74、2.31 cm。统计结果表明，多系统GNSS-PPP组合定位比单GPS-PPP在E、N、U 3个分量上的精度平均提升30.7%。

当前社会发展城市高楼密布，城市峡谷场景越来越多。本文进一步实验对比单GPS和多系统G/R/C/R高度截止角对定位精度的影响。图5显示高度截止角分别设置为10°、20°、30°和40°的E、N、U，以及可见卫星数和GDOP值。从图中可以看出：截止高度角超过20°后，GDOP值明显增大，可用卫星数显著降低；多系统组合PPP结果比单GPS优越且平稳。

图2 PPP动态定位ENU分量误差、卫星数以及GDOP时间序列

图3 GPS系统与GNSS组合系统的PPP动态解算收敛结果时间统计

3 结束语

针对目前GNSS定位技术发展方向，本文对多系统多频点PPP进行了研究，基于IGS-MGEX测站数据研究GNSS-PPP组合定位的精度以及性能。结果表明，多系统组合定位比单GPS系统在精度以及收敛时间上都有显著改善，E、N、U 3个分量精度平均提升30.7%，收敛时间降低55.3%。由于多系统组合定位增加了可见卫星数，因此截止高度角对GNSS-PPP定位结果影响较小。

致谢：感谢MGEX提供的多系统精密轨道和钟差产品以及多系统观测数据。

[1] LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009, 56(2): 135-149.

[2] GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. J Geodesy, 2008, 82(7): 389-399.

[3] GENG J, BOCK Y. GLONASS fractional-cycle bias estimation across inhomogeneous receivers for PPP ambiguity resolution[J]. J Geodesy, 2015, 33(10): 1-18.

[4] GENG J H, BOCK Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution[J]. J Geodesy, 2013, 87(5): 449-460.

[5] CAI C, GAO Y. Modeling and assessment of combined GPS/GLONASS precise point positioning[J]. GPS Solut, 2012, 17(2): 223-236.

[6] CAI C, GAO Y, PAN L, et al. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143.

[7] GUO J, XU X, ZHAO Q, et al. Precise orbit determination for quad-constellation satellites at Wuhan University: strategy, result validation, and comparison[J]. J Geodesy, 2015, 90(2): 143-152.

[8] LI X. Accuracy and reliability of multi-GNSS real-time precise positioning GPS, GLONASS, BeiDou, and Galileo[J]. 2015, 37(2): 303-315.

[9] 任晓东, 张柯柯, 李星星, 等. BeiDou Galileo GLONASS GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 8-15.

[10] 刘志强, 王解先, 段兵兵. 单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报, 2015(2): 10-18.

[11] ODIJK D, TEUNISSEN P J G, ZHANG B C. Single-frequency integer ambiguity resolution enabled GPS precise point positioning[J]. J Surv Eng-Asce, 2012, 138(4): 193-202.

[12] 郭靖. 姿态光压和函数模型对导航卫星精密定轨影响的研究[D].武汉大学, 2014.

[13] FENG Y M, GU S F, SHI C, et al. A reference station-based GNSS computing mode to support unified precise point positioning and real-time kinematic services[J]. J Geodesy, 2013, 87(12): 945-960.

[14] 张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100.

[15] 刘利, 时鑫, 栗靖, 等. 北斗基本导航电文定义与使用方法[J]. 中国科学: 物理学力学天文学, 2015, 45(7): 7950901-7950907.

[16] BIERMAN G J. Factorization methods for discrete sequential estimation[J]. 1977(5): 132-141.

[17] ZHAO Q, WANG C, GUO J, et al. Assessment of the contribution of BeiDou GEO, IGSO, and MEO satellites to PPP in Asia-Pacific region[J]. Sensors, 2015, 15(12): 277-285.

[18] 张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256.

Precision analysis of multi-system and multi-frequency points combined positioning for GNSS-PPP

XUE Erfeng, LYU Dengshen, ZHAO Tingbao

（Qinghai Geographic Information Industry Development Co., Ltd., Xining 810001, China）

In order to further promote precise point positioning (PPP) technology of global navigation satellite system (GNSS) and realize multi-GNSS-PPP engineering application, based on the data of International GNSS Service-multi GNSS experiment (IGS-MGEX) station, the paper studied the accuracy and performance of gnss-ppP: four GNSS integrated PPP technologies were introduced and analyzed; and the convergence time and positioning accuracy of PPP were tested by multi-system and multi-frequency positioning; then the positioning results of single GPS-PPP and multi-GNSS-PPP were comparatively analyzed for different height cutoff angles. Results showed that the accuracy and convergence time of multi system combined positioning could be significantly improved than that of single GPS system, the accuracy of ENU three components would be increased by 30.7% on average, and the convergence time would be reduced by 55.3%; moreover, due to the increase of the number of visible satellites in multi system combined positioning, the cut-off altitude angle could have little impact on the gnss-ppp results.

global navigation satellite system (GNSS); precision point position (PPP); combined positioning; convergence time; height cutoff angle

薛二锋, 吕登申, 赵廷宝. GNSS-PPP多系统多频点组合定位精度分析[J]. 导航定位学报, 2023, 11(4): 145-150.（XUE Erfeng, LYU Dengshen, ZHAO Tingbao. Precision analysis of multi-system and multi-frequency points combined positioning for GNSS-PPP[J]. Journal of Navigation and Positioning, 2023, 11(4): 145-150.）DOI:10.16547/j.cnki.10-1096.20230420.

P228

A

2095-4999(2023)04-0145-06

2022-03-07

薛二锋（1982—），男，河南信阳人，本科学历，工程师，研究方向为测绘工程与GNSS精密定位技术。