一道自主招生试题的简证及变式
2023-08-26 03:43湖南省桃江县第一中学413400胡芳举
中学数学研究(江西) 2023年9期
湖南省桃江县第一中学 (413400) 胡芳举
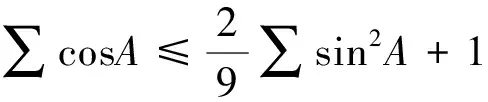
该题是一道自主招生试题形式优美,但证明较难,搜遍全网,只找到了一个解答(这个解答非常繁琐,见文[1]),本文将给出这个不等式的一个简证以及几个变式.
一、简证

要证原不等式,等价于证9∑cosA≤2∑sin2A+9=∑(1-cos2A)+9=12-∑cos2A⟺
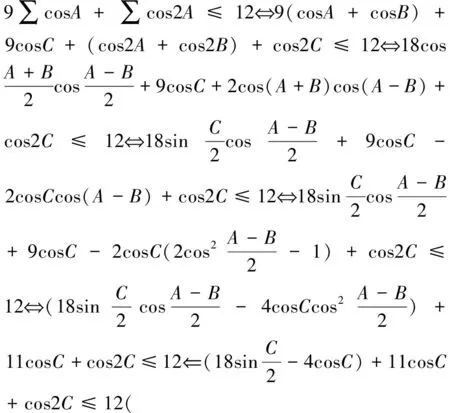
二、变式

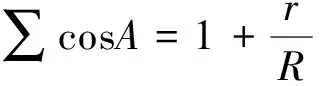
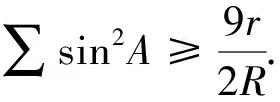
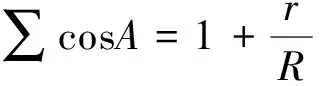
变式3 设ΔABC的内切圆半径为r,外接圆半径为R,三边长分别为a,b,c,则∑a2≥18Rr.
注:由正弦定理及变式2可得.
变式4 设ΔABC的内切圆半径为r,外接圆半径为R,外心与重心的距离为d,则R2-2Rr≥d2.

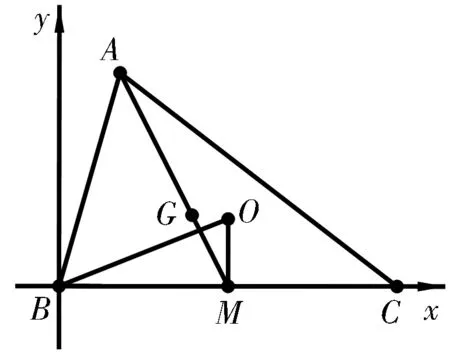
图1
变式5 已知正实数x,y,z满足x2+y2+z2+2xyz=1,则9(x+y+z)-4xyz≤13.
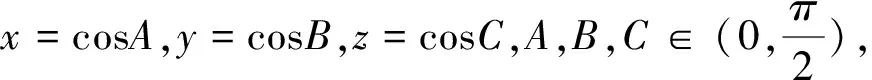
猜你喜欢
学校教育研究(2022年7期)2022-04-24
中学生数理化·高一版(2022年2期)2022-04-05
中学数学研究(江西)(2021年10期)2021-11-10
中等数学(2021年6期)2021-08-14
中等数学(2021年2期)2021-07-22
中等数学(2020年9期)2020-11-26
湖南农业(2020年5期)2020-01-09
中等数学(2018年7期)2018-11-10
中学数学杂志(高中版)(2018年1期)2018-01-27
幼儿画刊(2017年9期)2017-09-26

