一道联考题的命题背景及拓展*
湖南省常宁市第六中学 (421099) 王 丽
湖南省衡东县第一中学 (421400) 朱亚旸
湖南省常宁市第二中学 (421500) 王小国
一、考题再现
二、背景分析
本题的背景在人教A版教材有四处,分别如下:
背景1 (选择性必修二第88页综合运用)已知圆的一条直径的端点分别是A(x1,y1),B(x2,y2),求证此圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.
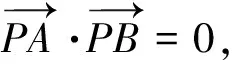
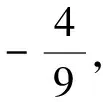
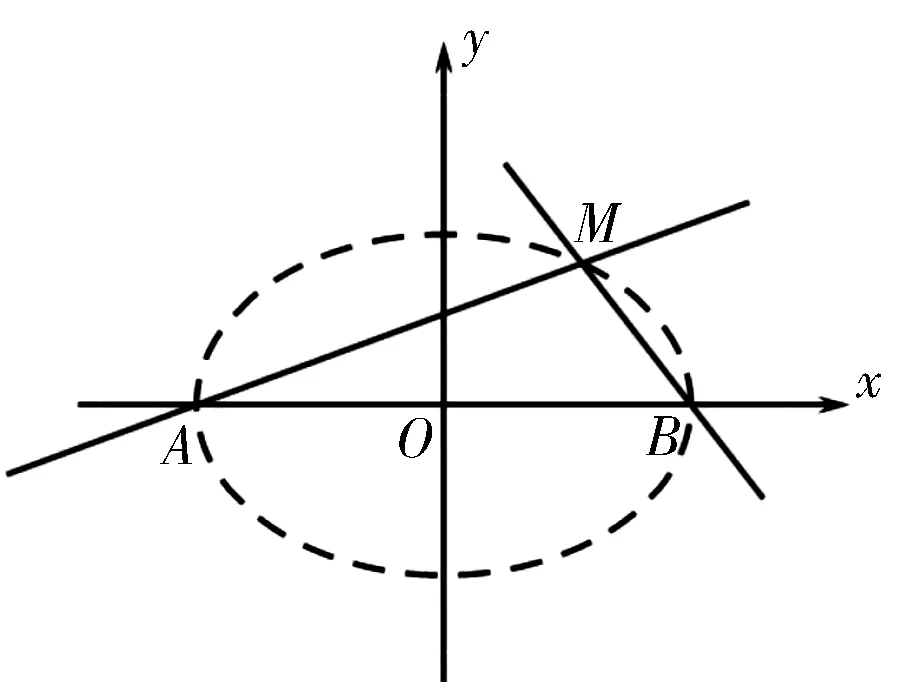
图1
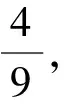
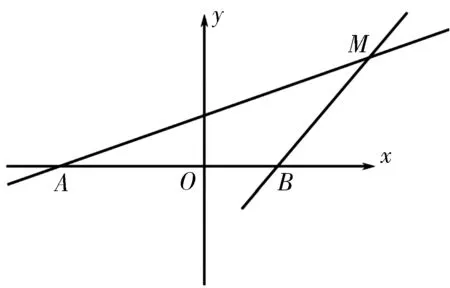
图2
背景4 (选择性必修二第146页第11题)已知ΔABC的两个顶点A,B的坐标分别是(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m(m≠0),求顶点C的轨迹.
以上四道教材习题都有共同的特征,存在关于轨迹的对称中心对称的两点A,B,对轨迹上任意点P,都有直线PA,PB的斜率之积为一个定值,其一般情形可以归结为:
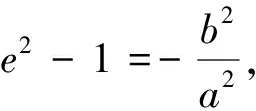
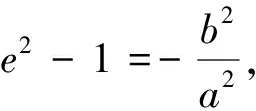
定理2 若AB为“有心圆锥曲线”的直径,点M为曲线上异于A,B的任一点,则kAM·kBM=e2-1.(圆可视为离心率为0)如图3.
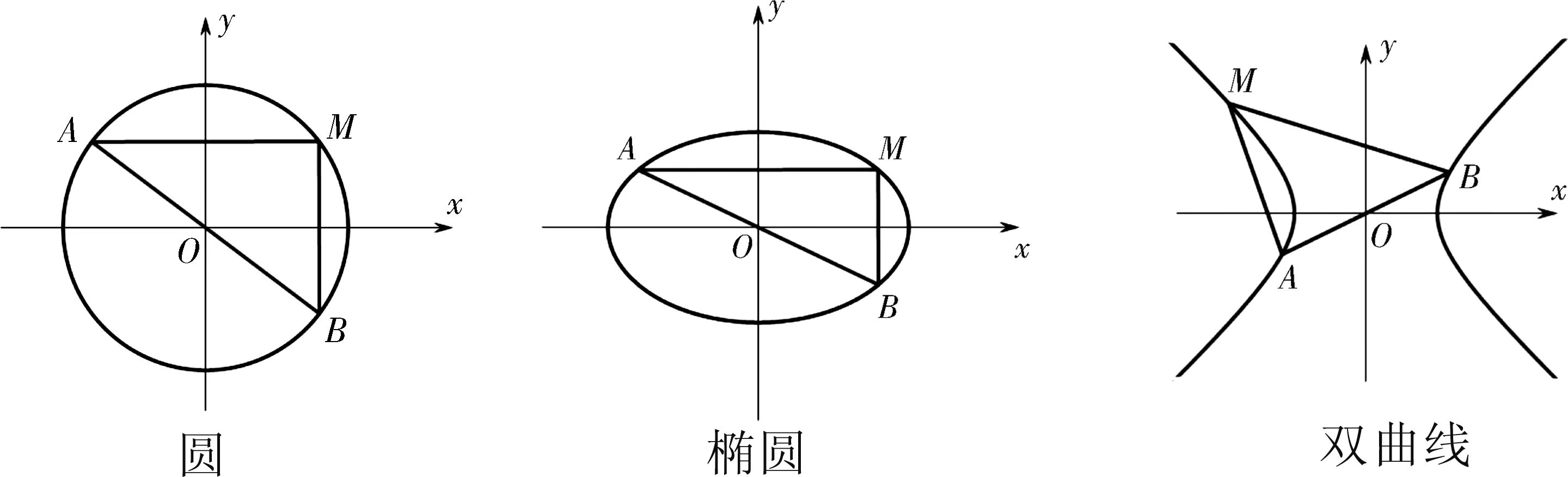
图3
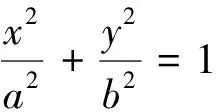
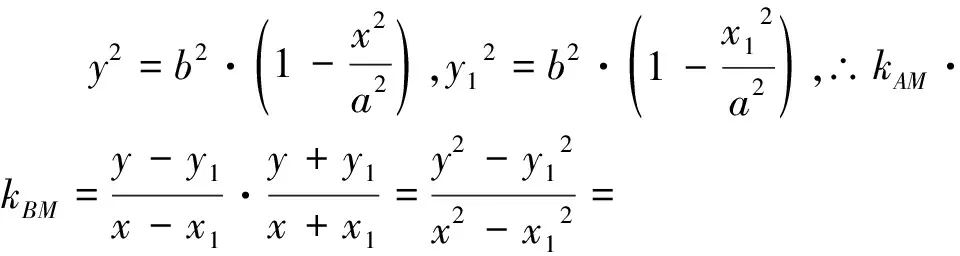
推论2若点M是“有心圆锥曲线”的弦AB的中点,其中AB不平行于对称轴且不过曲线中心O,则kAM·kBM=e2-1.如图4.
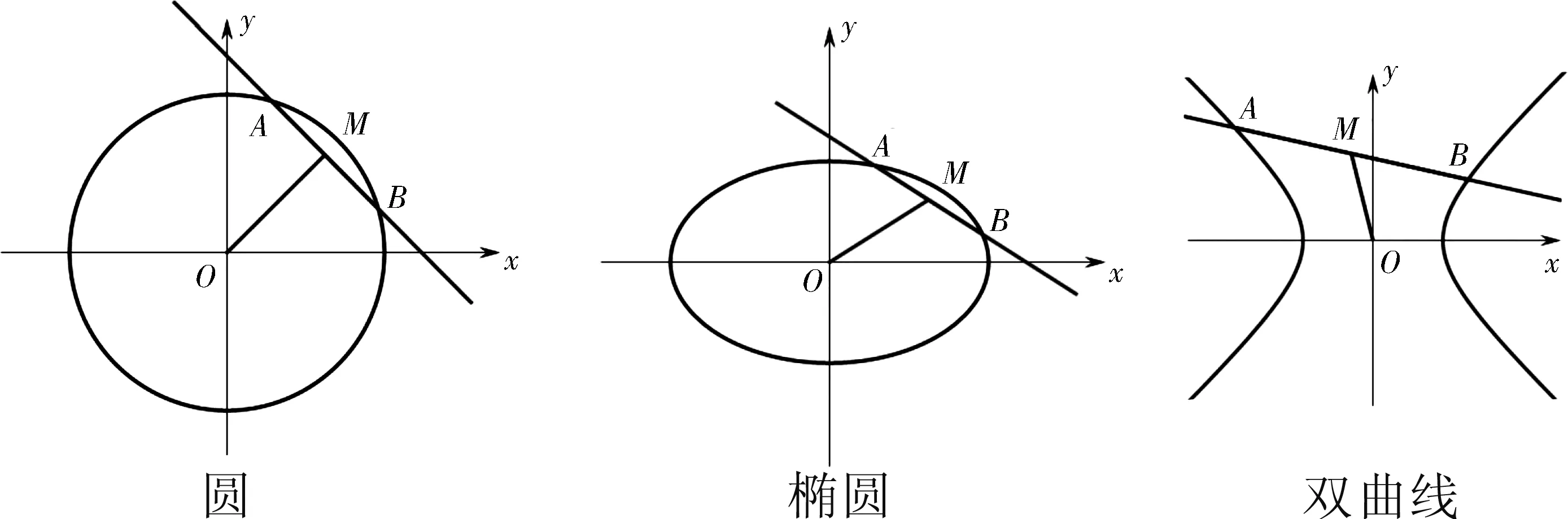
图4
我们现在用点差法对椭圆进行证明,双曲线、圆可类似证明.
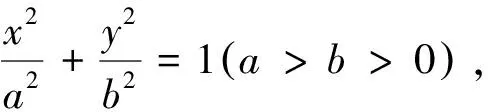
其本质与定理2是一致的,即kOM·kPB=kPA·kPB=e2-1.
利用上述结论,我们可容易给出考题的答案.
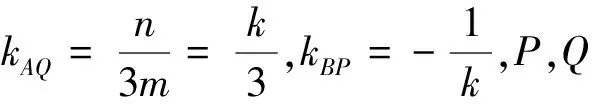
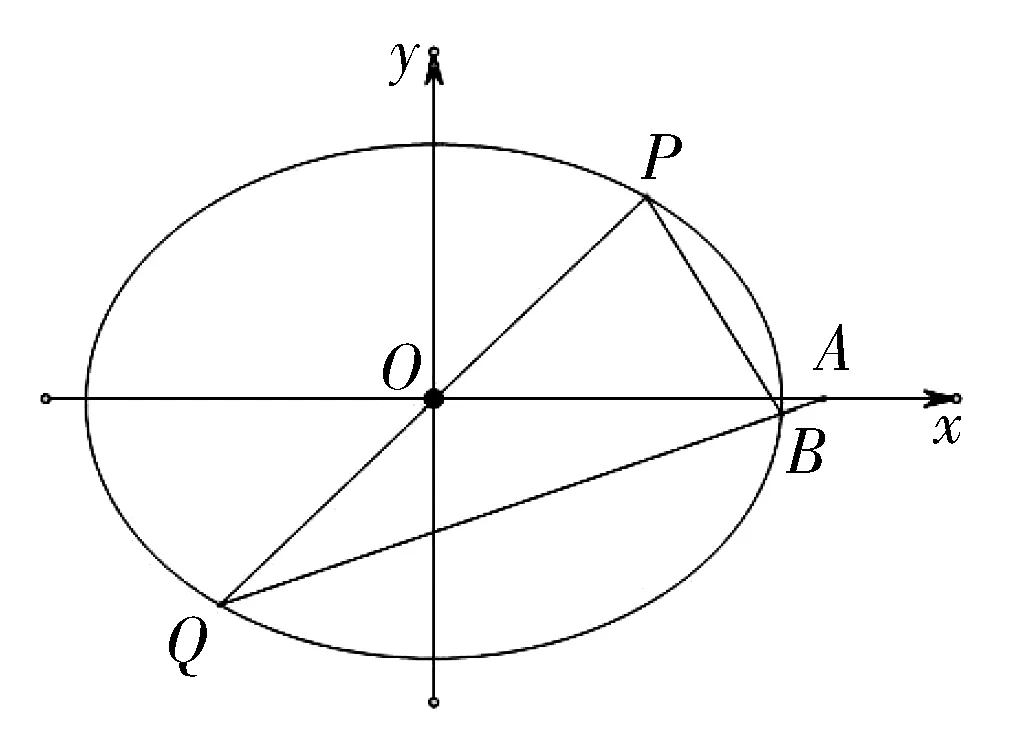
图5
三、试题链接
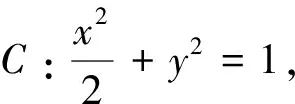
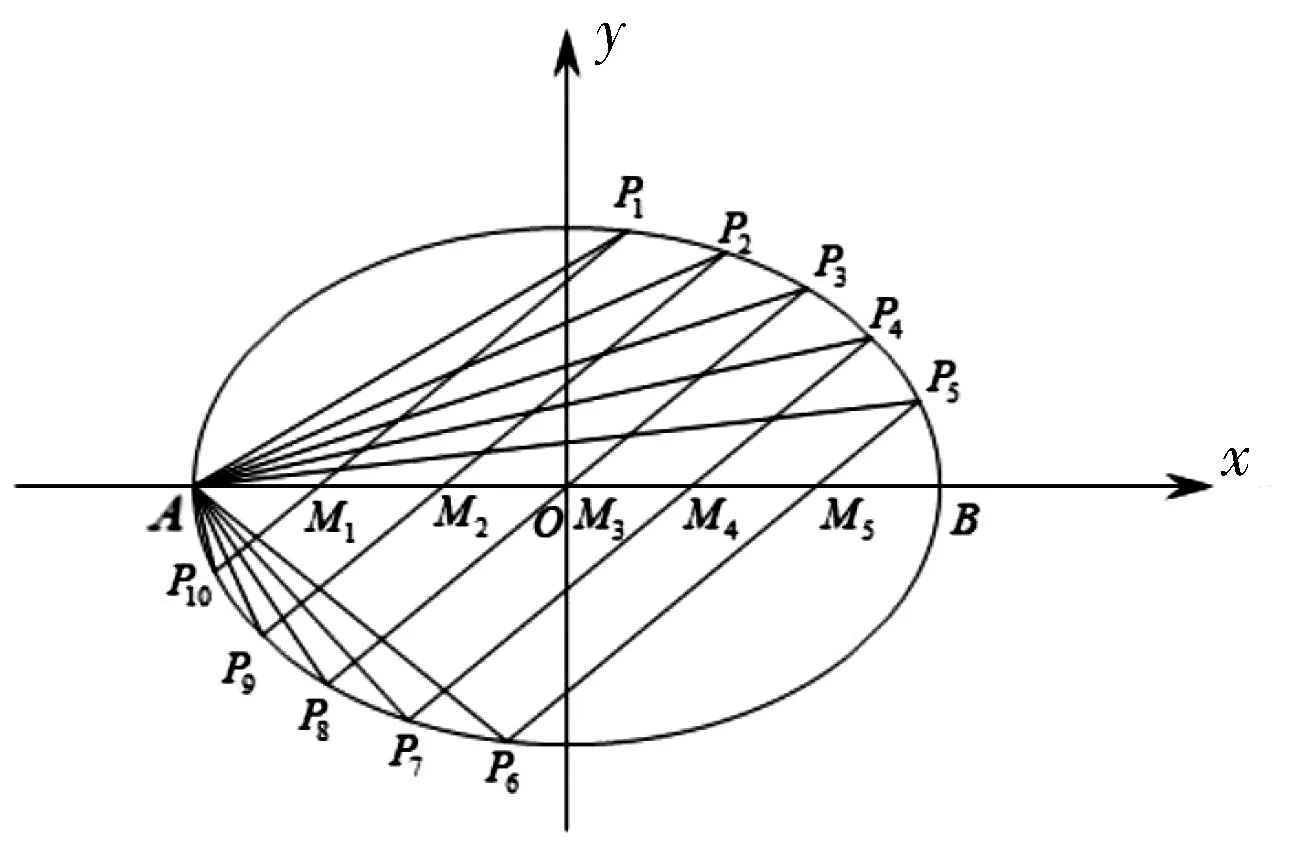
图6
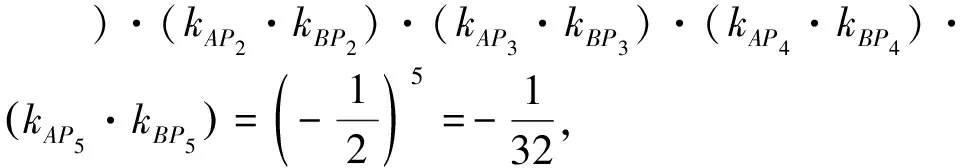
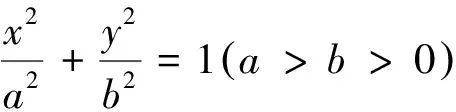
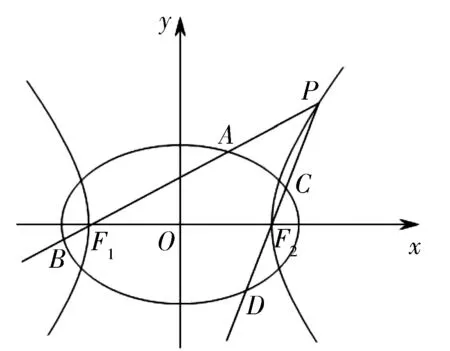
图7
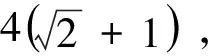
四、结语
中学数学教材中的习题凝聚了几代数学教育家的智慧,具有典型性、示范性、迁移性等特点.其背后隐藏着深远的数学背景,是高考数学试题命题的附着点与根源,具有深刻的研究价值.纵观近十年的高考数学题,大量命题都与教材关联密切.因而,作为教师在指导学生高三数学复习时要适时回归教材,通过对教材中有价值的材料以及拓展资源,链接历年高考试题,培养学生能系统地对教材进行深入思考,深度挖掘,延申拓展的意识,深度整合并展示其共性规律,帮助学生完善知识网络,促进深度学习.也让教材成为提升学生思维能力的一种工具,基于此,在数学问题求解中,便能借助模型、规律的敏感性,既使得问题化繁为简,事半功倍!也能火眼金睛,看清问题之本质.

