基于空间域dP/dV计算的光伏控制方法

倪佳华，项基，赵波

(1.浙江大学 电气工程学院，浙江 杭州 310027；2.国网浙江省电力有限公司电力科学研究院，浙江 杭州 310014)

在“双碳”目标下，光伏因其绿色、低碳和低维护成本等优势，成为最有发展前景的新能源之一[1].光伏的输出功率总是受温度和辐照度的影响，存在不确定性和随机性波动.学者们一直致力于提升光伏输出性能，以满足不同的电网需求[2-4].通常，光伏控制方法追求无稳态振荡和快速收敛，因为稳态振荡会导致功率损耗并恶化电能质量，而缓慢的收敛意味着长时间运行偏离最大功率点，导致光伏利用率降低.

扰动观测法(perturb and observe，P&O)[5-7]和增量电导法(incremental-conductance，InC)[8-9]因其结构简单和实施方便，得到了广泛的应用.传统的P&O和InC方法基于试错，寻找和跟踪最大功率点(maximum power point，MPP).在选择扰动步长时需要权衡：较大的值带来更快的动态响应，但在稳态下会增加MPP周围的振荡；较小的值能够弱化稳态振荡，但会减慢动态响应.在选择迭代步长时，存在动态性能和稳态性能之间的权衡.

有些学者通过优化扰动步长，改善稳态和动态性能.Liu等[10]提出变步长的增量电导法，扰动步长正比于功率关于电压导数(dP/dV)的绝对值.在MPP附近，dP/dV趋近于零，则步长也能趋于零.Fathabadi[11]同时考虑功率关于电压的导数(dP/dV)和功率关于电流的导数(dP/di)，根据两者的值设置5个阈值来选取合适的步长.Zhou等[12]利用电流和功率关于电压的导数(dP/dV)来设置步长变化系数，以期获得平滑的步长变化曲线.Tafti等[13]提出柔性的自适应扰动观测方法跟踪指定功率，根据dP/dV设计稳态期间的迭代电压步骤，以实现稳定的恒功率输出.上述的步长优化方法都利用了以下光伏特性：越接近MPP，dP/dV的绝对值越小.虽然动态跟踪速度有所提高，但是由于零分母约束和时域dP/dV或dP/di计算的噪声敏感性，稳态振荡仍然存在.有些方法尝试引入状态识别模块，通过模式切换暂停扰动，以消除振荡.李向丽等[14]利用MPP点附近压差符号变化的特性来识别稳态.Bhattacharyya等[15]在变步长的P&O和InC方法基础上，增加了稳态识别模块.当光伏电压连续3次符合稳态电压振荡模式时，暂停扰动，以消除稳态振荡.为了在环境变化下重启扰动观测模块，需要增加动态识别模块，这会增大控制复杂度，为了防止误判而增加的阈值又会影响输出性能.

光伏控制需要简单、高效的方法，光伏的P-dP/dV特性提供了这种潜力.由于dP/dV和光伏输出功率之间存在对应关系，Cai等[16]把dP/dV当作控制量直接进行控制，将光伏输出的dP/dV控制为零，能够实现最大功率输出，无需试错和其他先验知识.将输出的dP/dV控制在负值，还能使光伏运行在功率热备模式.光伏输出性能不是文献[16]的重点，使用的是时域的dP/dV计算方法，由于零分母问题，稳态振荡仍然存在.当前的研究空白是缺乏有效、鲁棒的dP/dV计算方法来提高基于dP/dV控制方法的性能.

本文提出基于空间域dP/dV计算的控制方法，旨在为上文提出的问题提供可行的解决方案.本文采用二维数组来构建空间域，利用基于电压索引的历史运行数据维护空间域.每一次dP/dV计算都使用当前的运行数据和在空间域中相邻的历史数据，可以避免零分母问题，以实现不同dP/dV参考值下的零误差跟踪和零稳态振荡.该方法在最大功率跟踪(maximum power point tracking,MPPT)(dP/dV= 0)和功率热备运行模式(dP/dV＜0)下都取得了较好的输出性能.

1 光伏特性

基于均匀光照下的光伏数学模型揭示光伏P-V和P-dP/dV的特性，以明确dP/dV在光伏控制中的作用.

1.1 P-V特性

理想的光伏阵列数学模型为

式中：ipv和Vpv分别为光伏输出电流和电压；Np和Ns分别为串联和并联的光伏模块个数，每个光伏模块由N个单元构成；q、K、T分别为元电荷数、波尔兹常数和模块温度；Isc,N、I0,N和a分别为光伏模块短路电流、二极管漏电流和二极管理想常数.Isc,N和I0,N是随辐照度E和温度T改变的.光伏模型的进一步阐述可以参照文献[17,18].

由此，光伏阵列的输出功率可以表示为

从式(2)可知，光伏输出功率和电压之间是非线性相关的，且受环境辐照度和温度的影响.这意味着在不确定的环境条件下，光伏的输出具有随机性和间断性.如图1 (a)所示，为了直观地理解这一特性，绘制了KC200GT光伏阵列在不同辐照度和温度下的P-V曲线.图中，每条曲线都有1个最大点和2段被最大点分割的线段，最大点表示光伏阵列在特定环境条件下能产生的最大电量.在最大点左侧，输出功率随着电压的增加而增加；在最大点右侧，输出功率随着电压的增加而下降.在不断变化的环境条件下，可用功率（最大功率）随之波动.

1.2 P-dP/dV特性

功率对电压的导数可以表示为

功率对电压的二阶导数为

显然，式(4)恒小于零，即dP/dV是单调递减的.dP/dV的极值点为

由式(2)～(5)可得以下结论.1）在区间[0,Uoc]内存在一点Vpv=Ump，该点处的输出功率为最大值Ppv=Pmax且dP/dV =0.2）在区间[0,Ump]内，随着电压的增加，dP/dV减小，功率增大.3）在区间[Ump,Uoc]内，随着电压的增加，dP/dV减小，功率减小.4）在区间[Ump,Uoc]内，功率相对于电压的变化率更大.

如图1 (b)所示为同一个KC200GT光伏面板的P-dP/dV曲线.各P-dP/dV曲线特性均符合上述结论：光伏输出功率可以通过dP/dV调节；当dP/dV= 0时，无论环境条件如何变化，光伏面板始终工作在最大功率点；当dP/dV为负值时，光伏面板削减一部分功率而工作在功率热备模式，且dP/dV越小，削减的功率比例越大.

2 基于空间域dP/dV计算的控制算法

如图2所示为基于空间域dP/dV计算的控制结构.所提方法移除了P&O模块，把dP/dV作为控制变量直接进行控制.dP/dV参考值由上层控制给定， dP/dV实际值基于当前工作点电压和电流计算得到，两者之间的差值经过比例积分模块生成占空比d.实现该控制方法的关键在于dP/dV的计算，也是本文的创新之处，即空间域dP/dV的计算方法.

图2 基于空间域dP/dV计算的光伏系统控制结构Fig.2 Spatial-domian dP/dV calculation based PV control scheme

2.1 空间域dP/dV计算原理

通过和时间域dP/dV计算原理的对比，揭示空间域dP/dV计算原理.在时间域dP/dV计算中，一般用2个连续时刻的运行点数据计算dP/dV，表达式为

式中：(dP/dV)t为t时刻的dP/dV，(Pt,Vt)为t时刻的功率和电压，(Pt-1,Vt-1)为t-1时刻的功率和电压.

式(6)的计算方法存在缺陷：当输出趋于稳态的时候会发生零分母问题，即|Vt-Vt-1|→0.一般有2种方法来识别零分母问题.1）检测电压的变化，当2个电压接近到一定程度（|Vt-Vt-1|＜UTH）时，这2个电压视为相等.2）检测异常计算值，当零分母情况出现的时候，dP/dV的计算值会超过正常范围，即|(dP/dv)t|＞MAXTH.在传统的扰动观测算法中，当零分母情况被识别后，会停止扰动，以实现稳态下的无振荡输出.在环境变化后，需要动态检测模块来重启扰动观测算法，以跟踪最新的运行点.状态检测和模式切换的方式不但增加了控制的复杂度，而且会影响算法的输出性能.

提出空间域dP/dV计算方法，避免稳态下的零分母问题.通过2个空间上相邻的运行点来计算dP/dV，运算表达式为

式中：(Pt-k,Vt-k)为t-k时刻的功率和电压，其在空间上和当前t时刻的值相邻.

对比式(6)、(7)可知，空间域和时间域之间的区别在于(Pt-k,Vt-k)的选择.在时间域中k始终取1，在空间域中n可能是任意正整数，只要满足(Pt-k,Vt-k)在空间上和当前运行点(Pt,Vt)相邻.因为空间上的两点始终存在一定的距离，可以避免稳态下零分母问题的出现.

2.2 空间域dP/dV计算的实现方法

为了建立空间域，定义如图3所示的二维数组Data().图中，每一列表示空间域中的一个位置，用来存放某一时刻的电压、电流.每一处存放的电压Ui和列序号i之间都满足下式：

图3 空间域的定义Fig.3 Definition of spatial-domain

式中：M为数组长度，δ为空间间隔，·」为向下取整运算符.

下面通过举例说明空间域的存储过程.设在ta时刻，运行点数据为(Ua,Ia)，则数据应该存储在列序号为Ua/δ」的位置，即

在另一时刻tb，运行点数据为(Ub,Ib)，则数据应存储在列序号为Ub/δ」的位置，即

每一次dP/dV的计算都取空间域中的2列数据，一个是当前运行点数据，另一个是空间上相邻的数据.如图4所示为空间域dP/dV计算的流程图.在数组初始化后，控制器循环执行以下操作：

图4 空间域dP/dV计算的流程图Fig.4 Flowchart of spatial-domain dP/dV calculation

采样当前光伏运行点的电压Um和电流Im，并存储到相应位置：

式中：m=Um/δ」.

向后找到距离m列最近的非空列n，即

式中：Ω={m+1,···,M}.

计算dP/dV，即

式中：(Um,Im)为当前时刻的运行点数据，(Un,In)为在空间域中和当前时刻相邻的数据.

2.3 参数设定

1）数组长度M.数组是用来存储运行中采样的数据，必须能够存放运行中最大电压下的数据，即

式中：Eref、θref为标准测试条件(1000W/m2、25 ℃)下的参考辐照度和温度；θmax为最大辐照度，θmax为最大温度，均由运行环境决定；β为Uoc的温度系数，a为温度修正系数，均由光伏面板厂家提供.

2）空间间隔δ.δ和dP/dV的跟踪精度和速度有关，下面将从这2个角度展开分析.

a)如图5所示为dP/dV在不同δ下的跟踪精度.B点是dP/dVref对应的理想工作点，图中不同色块表示电压存储间隔.如图5(a)所示为在较大的空间间隔δ1下的跟踪过程，如图5(b)所示为在较小的空间间隔δ2下的跟踪过程.

图5 不同δ下的dP/dV跟踪精度Fig.5 Accuracy of dP/dV tracking with different δ

光伏P-V曲线可以近似地拟合成抛物线[20]：

式中：a2、a1、a0为二次项系数.

设B点和C点的坐标为

式中：UB、P(UB)分别为B点的电压和功率；λ为常系数(0＜λ＜1.0)；λδ为B点和C点之间的距离，距离和δ有关.

如图5所示，在稳态时AC直线的斜率等于B点的斜率，满足下式：

式中：UA、P(UA)分别为A点的电压和功率，P′(UB)为B点的一阶导数.

结合式(16)、(18)，可得

即稳态点和理想点的电压偏差为λδ.由此可得，δ越小，则电压偏差越小，跟踪精度越高.该结论体现在图5中，空间间隔较小的稳态点A更接近B点.

b)如图6所示为在环境变化时不同的δ下dP/dV的跟踪响应速度.图6 (a)中，曲线l1和l2是光伏在不同环境条件下的P-V曲线，而曲线l1的最大功率点更高.以曲线从l2到l1变化为例，空间域计算的直线斜率变化是从KA2C2到KA1C2.

图6 不同δ下的dP/dv跟踪快速性Fig.6 Celerity of dP/dv tracking with different δ

为了从数学角度阐明δ的影响，设B2点和C2点之间的电压差是δ，直线B2C2的斜率是KB2C2=k，从B2点到B1点功率增加ΔP.

由此，可以确定B1和C2点的坐标如下：

则直线B1C2的斜率为

环境变化导致空间域计算下dP/dV的改变量为

其中ΔP＞0.在同样的环境变化下，δ 越小，则dP/dV的改变量越大，即响应速度更快.

空间间隔越小，则跟踪精度越高，且对环境变化的响应速度越快，所以理想情况下δ的取值越小越好.在实际部署时，需要考虑2个硬件限制条件.1）存储空间有限，δ越小，则空间域数组越长，占用存储空间越大.2）采样分辨率有限制，δ越小，则电压差受测量误差的影响越大.根据实验测试经验，推荐取最小采样刻度ε的5到10倍.

式中：N为数字采样分辨率.

3 仿真结果

为了验证所提算法的有效性，在MATLAB/Simulink中进行一些测试.光伏系统的电路结构和图5中一致，标准测试条件（辐照度为1 000 W/m2，温度为25 ℃）下的系统参数如表1所示.

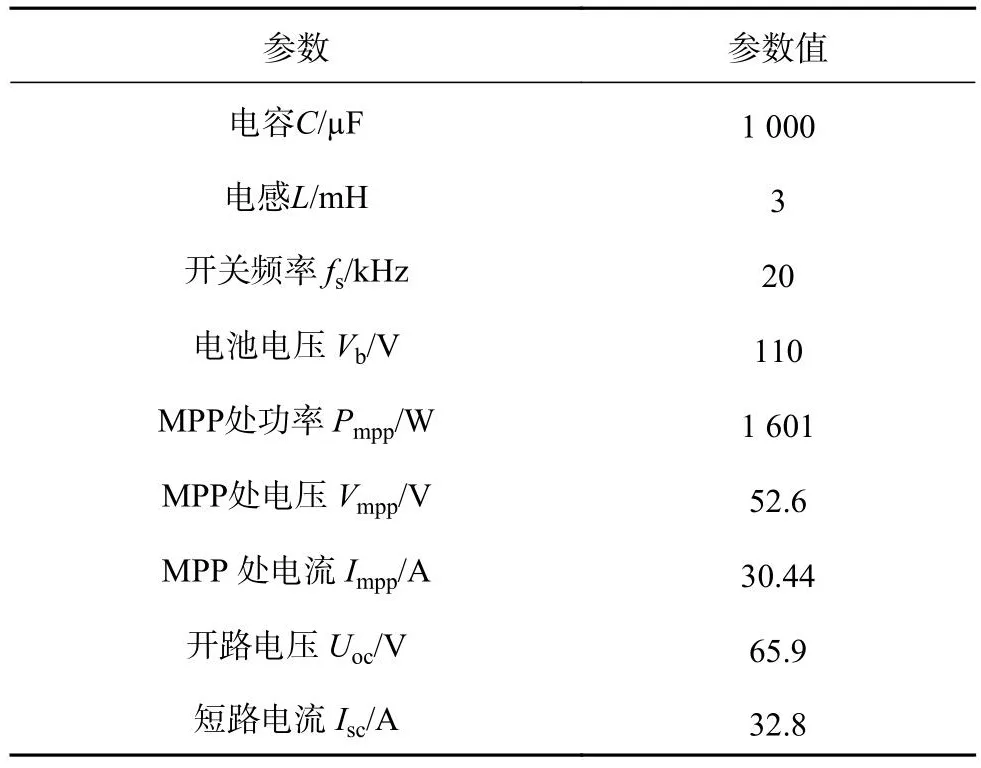
表1 光伏系统参数Tab.1 PV System Parameters

测试分为以下2个场景.1）最大功率跟踪性能.评估所提控制算法在辐照度恒定、斜坡变化和阶跃变化下的最大功率点跟踪性能，和其他2种算法进行对比.2）功率热备性能.在辐照度恒定的环境条件下，评估所提控制算法在不同dP/dV参考值下的输出性能，并和基于时域dP/dV计算的算法进行对比.

3.1 MPPT性能对比

所提算法中的dP/dV参考值设置为0，以实现MPPT功能.在相同的环境条件下，对提出的方法、最流行的经典P&O-MPPT算法和最新的SOFT-MPPT算法[15]进行比较.温度恒定为25 ℃，辐照度变化如下.1) 辐照度的初始值为600W/m2.2) 第4 s时，辐照度跃变上升到1 200W/m2；第4.0～7.0 s时，辐照度保持在1 200W/m2.3) 第7.0～11.0 s时，辐照度以50W/(m2·s)的速率减小.4) 第11.0～12.0 s时，辐照度保持在1 000W/m2.

如图7 (a)所示为经典P&O MPPT算法的仿真结果.图中，Ve为电压误差，Pe为功率误差.经典P&O方法以固定步长搜寻MPP.利用该算法，实现了3种不同太阳辐照度下的最大功率点跟踪.固定步长扰动会在MPP附近带来稳态振荡.可用功率越高，功率损耗越大.减小稳态振荡的一种自然方法是减小步长.较小的步长会导致较慢的动态响应，反之亦然.

图7 不同MPPT算法下的光伏输出Fig.7 PV output with different MPPT algorithms

SOFT-MPPT方法采用基于dP/dV的变步长扰动观测和稳态识别机制，以实现快速的动态响应和零稳态振荡.如图7 (b)所示，当辐照度在4 s时以阶跃方式变化时，dP/dV的计算偏差导致电压发生较大偏移，这种偏移需要较多的扰动步骤才能达到稳态.由于时域dP/dV计算的零分母问题，在稳态时存在振荡，SOFT-MPPT算法利用稳态检测模块来识别稳态振荡的电压模式.一旦检测到电压模式，则算法会停止扰动观测模块，并工作在恒电压模式.为了在环境变化后重启扰动观测模块以跟踪新的最大功率点，算法增加了动态检测模块.为了防止误判，动态检测模块需要满足一定的裕量，这导致了动态响应的滞后.如图7(b)所示，虽然辐照度从第7 s时开始变化，但是算法在0.5 s后才重启扰动观测模块.因为稳态检测模块存在裕量以防止误判，当辐照度从斜坡变化变为恒定时，辐照度变化积累的误差仍在裕量内，导致过早的收敛而存在电压偏差，即11 s后，扰动观测模块没能重启以跟踪新的最大功率点.

如图7 (c)所示，利用本文方法实现了更快的动态跟踪和无稳态振荡.虽然在第4 s辐照度发生突变时，光伏电压发生了较大的振荡，但是在极短的时间内达到了稳态.这一快速动态响应得益于以dP/dV作为控制变量，跟踪误差可以通过反馈控制实时响应输出.在所提的空间域dP/dV计算模块中，dP/dV的计算不会出现零分母问题.dP/dV可以稳定在参考值，利用光伏系统可以实现无误差跟踪并消除稳态振荡.虽然在辐照度斜坡变化下，与SOFT-MPPT算法相比，所提算法表现不突出，但是所提算法对辐照度变化的响应更快，且在辐照度稳定后能够更精确地跟踪新的最大功率点.在第7 s辐照度开始变化时，所提算法在极短时间内响应了该变化.在第11 s辐照度停止变化后，快速跟踪到了最新的最大功率点.

3.2 功率热备运行性能对比

基于dP/dV调节光伏输出是便捷的方法.Cai等[16]用dP/dV控制作为内环来满足外环的控制需求，但是用到了时间域dP/dV的计算方法.为了表明本文所提空间域dP/dV计算方法的优势，在相同的条件下进行对比.环境参数保持在标准条件(1 000W/m2, 25 ℃)；第2～6 s时，dP/dV参考值为0；第6～10 s时，dP/dV参考值为-100；第10～14 s时，dP/dV参考值为-150.

如图8所示为2种方法在不同dP/dV参考值下的仿真结果.光伏输出与1节分析吻合.当dP/dV=0时，光伏输出最大功率；当dP/dV＜0时，光伏预留一定功率，且dP/dV越小，光伏预留功率越大.如图9 (a)所示，基于时间域dP/dV计算方法会引入严重的稳态振荡.第6～8 s时，功率振荡幅值高达150 W.振荡的发生源于时间域计算在稳态下存在零分母问题，Cai等[16]人为地施加扰动，以避免零分母问题.图9 (b)中，利用本文方法得到的稳态功率振荡值最大为3 W(0.2%)，得益于空间域计算方法的无零分母优势.

图8 不同dP/dV计算方法下的功率热备输出Fig.8 Power reserved mode with different dP/dV calculation methods

图9 光伏发电实验装置Fig.9 PV generation experimental setup

4 实验分析

为了进一步说明所提算法的有效性，开展实物实验，实验设备如图9所示，电路结构和图2一致.升压变流器输入侧为光伏面板，型号为DJB-18V100WK，输出侧接48 V锂电池.主控芯片为STM32F030K6T6，主频为48 MHz，闪存为16 kB，静态随机存取存储器为4 kB.将光伏面板安装在无遮挡的实际环境中，以获取均匀的辐照度.

由于实际环境条件复杂且具有不确定性，为了获得相对公平的结果，在70 s内依次对比了各算法的表现，各算法的环境条件视为一致.温度θ和辐照度E的变化曲线如图10所示，温度最高为33.4 ℃，最低为32.9 ℃，辐照度最高为547 W/m2，最低为545W/m2，忽略随机的波动，环境条件可以看作为恒温、恒辐照度.

图10 辐照度和温度的变化曲线Fig.10 Change curves of irradiance and temperature

与仿真类似，测试2种场景下的算法性能对比：最大功率跟踪和功率热备运行.每一种算法的参数都调整到最优，以输出最佳性能.在各算法启动前，光伏系统保持在17 V恒压输出.如图11～15所示为各算法的示波器输出波形图，每张图下方的左侧箭头表示算法启动，右侧箭头表示算法停止.

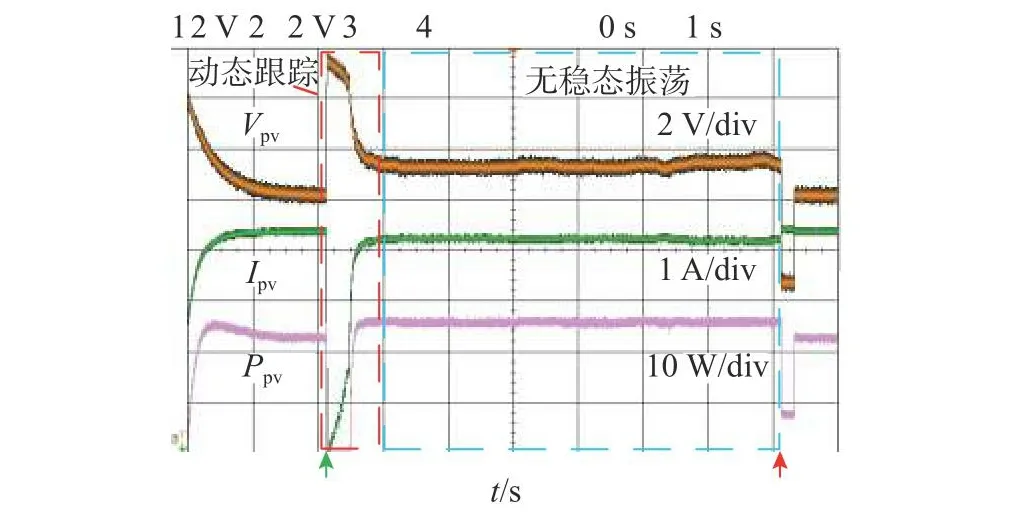
图11 基于所提空间域dP/dv计算方法的光伏输出Fig.11 PV behaviors with proposed spatial-domain dP/dv calculation method

图12 传统P&O MPPT算法下的光伏输出Fig.12 PV behaviors with conventional P&O MPPT algorithm

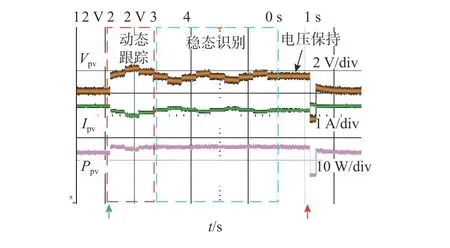
图13 SOFT-MPPT算法下的光伏输出Fig.13 PV behaviors with SOFT-MPPT algorithm

4.1 MPPT性能对比

如图11～13所示为3种不同MPPT算法的实验结果.3种算法都从输出电压17 V开始搜寻最大功率点，实现了最大功率跟踪达到稳态.从图11～13中虚线框内的系统表现可知，所提算法的收敛时间最短，传统P&O算法的收敛时间最长.因P&O算法步长是固定的，SOFT-MPPT算法用到了可变步长，第1步步长较大，因此SOFT-MPPT算法较传统P&O算法更快.

这3种方法的稳态性能与仿真结果一致.采用所提算法实现了无稳态振荡，传统的扰动观测方法围绕MPP振荡，SOFT-MPPT方法在检测到振荡的电压模式时暂停扰动观测模块，以消除振荡.与仿真结果不同，SOFT-MPPT方法会花费更多的步骤来识别稳态，因为稳态识别的判断受到噪声和测量误差的影响.

4.2 功率热备运行对比

如图14、15所示为基于时间域dP/dV计算的算法[16]和基于所提空间域dP/dV计算的算法的实验结果.2种算法采用相同的控制参数，以对比2种dP/dV计算模块的性能.各算法的测试都持续15 s，可以分为3个阶段，每个阶段的dP/dV参考值不同.阶段I的dP/dV参考值为0，阶段II的dP/dV参考值变为-5，阶段III的dP/dV参考值为-10.2种算法都在阶段I实现了最大功率跟踪，并在阶段II、III实现了功率热备运行，且dP/dV参考值越小，预留的热备功率越多，与1节分析的P-dP/dV特性相符.受开关器件和噪声的影响，实际输出波形不如仿真结果理想，但控制效果可以在波动幅度上进行比较.结果表明，由于时域dP/dV计算的零分母问题增加了稳态振荡，时域方法的电压波动几乎是空间域方法的2倍.

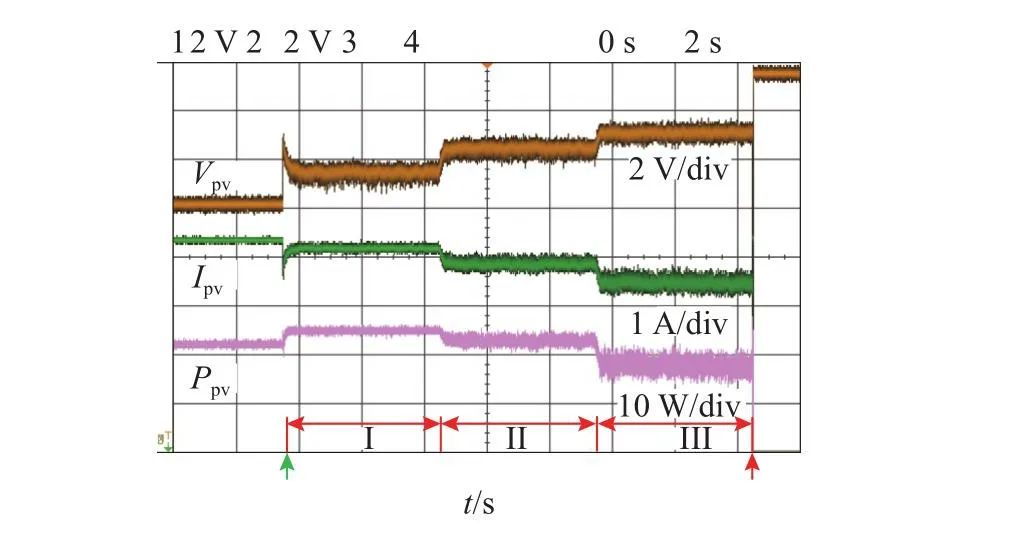
图14 基于时域dP/dV计算的方法在不同dP/dV参考值下的光伏输出Fig.14 PV output of time-domain dP/dV calculation based control method under different dP/dV references

图15 基于空间域dP/dV计算的方法在不同的dP/dV参考值下的光伏输出Fig.15 PV output of spatial-domain dP/dV calculation based control method under different dP/dV references

5 结 论

(1)本文阐述了所提控制方法的运行机制和空间域dP/dV计算的工作原理，说明了该控制方法相对于时间域dP/dV计算的优越性.

(2)提供了空间域dP/dV计算的实施流程图和参数设置方法.

(3)通过仿真和实验测试，验证了基于空间域dP/dV计算的控制方法的有效性.与传统的P&O方法和最新的SOFT-MPPT方法进行比较，证明了所提方法在最大功率跟踪方面的优越性；与基于时间域dP/dV计算的控制方法进行比较，证明了在功率热备运行控制上的优势.