室内缩尺级配堆石料力学参数的表征单元体积

王晋伟，迟世春，闫世豪，郭宇，周新杰

(1.大连理工大学 海岸与近海工程国家重点试验室，辽宁 大连 116024；2.大连理工大学 水利工程学院，辽宁 大连 116024)

堆石料广泛应用于堆石坝、机场高填方地基、路基等工程[1].由于堆石料原型级配的最大粒径达到800～1 000 mm，目前基于缩尺级配的室内三轴试验常被用于确定堆石料的等效力学参数，然后用于堆石坝变形预测的数值分析[2].孔宪京等[3]的研究表明，基于缩尺级配得到的力学参数可能会低估缩尺前的变形，高估堆石坝的安全性，且三轴试样尺寸的大小会影响试验结果.堆石料尺寸效应是堆石坝设计必须考虑的关键问题之一.

目前，堆石料尺寸效应的研究主要是对直径≤300 mm的试样进行常规三轴试验，建立不同最大粒径粗粒料的力学参数随最大粒径的变化规律，根据该规律外推原型级配的参数.许多研究得出的力学参数随粒径的变化规律存在一定的差异，甚至出现相反的结论.这可能与采用的密度控制条件、缩尺方法、颗粒形状及强度的不同有关[3].近年来，大连理工大学和中国水利水电科学研究院先后建成了直径为1 000 mm的特大型三轴仪，可以减小室内试验外推原型级配参数的误差并深入研究堆石料尺寸效应的机理，但无法直接对原型级配堆石料开展试验.能够突破室内条件限制的离散元方法（DEM）已经被用于研究堆石料的力学行为[4-5].若采用DEM模拟原型级配堆石料并找到可忽略其力学参数尺寸效应的试样尺寸，则有助于研究堆石料尺寸效应，探究大坝变形数值分析中存在的“低坝算大、高坝算小”问题.

表征单元体积（REV）指材料宏观力学行为趋于稳定的最小体积，反映了介质力学行为的尺寸效应，最早由Bear[6]提出，现被广泛用于固体和颗粒材料中.刘海涛等[7-9]通过试验或模拟研究试样尺寸对谷物和砂土的影响，得到相关物理和力学参数的REV.相比于上述颗粒材料，堆石料级配范围较宽且颗粒更易破碎[10-11]，所以研究试样尺寸对堆石料力学行为的影响时，须考虑颗粒排列和颗粒破碎.鉴于DEM评估原型级配堆石料力学参数REV的复杂性，结论无法通过室内试验直接验证.Holtz等[12-16]基于室内试验研究试样尺寸对缩尺级配堆石料强度参数的影响，在此基础上，现行规范GB/T 50123[17]和ASTM D7181[18]分别建议粗粒土室内三轴试验采用的试样直径与最大颗粒粒径的比值Rd不应小于5和6，所以本文对有室内试验参照的缩尺级配开展模拟.此外，现行规范参照的文献[12～16]中所建议的Rd均根据强度参数确定，而许多研究指出材料的变形特性受试样尺寸的影响[19-23]，因此需要进一步研究变形参数的REV.

本文采用DEM，研究试样尺寸对室内缩尺级配堆石料力学行为的影响.通过一系列室内单颗粒破碎试验分析玄武岩颗粒的破碎特性，确定DEM模拟所需的颗粒破碎强度参数.开展一系列试样尺寸、颗粒排列和围压不同的三轴压缩DEM试验.分析强度和变形参数随试样尺寸的变化规律，建议各参数的REV.

1 室内单颗粒破碎试验

堆石颗粒破碎试验设备选用大连理工大学研制的DYQ-1单粒岩块强度测试仪（见图1），最大加载能力为60 kN，加载方式可选位移或力控制.试验材料为古水面板坝玄武岩堆石料，采用定制圆孔筛筛出粒径为15～20、20～24、24～28、28～32、32～36和36～40 mm的6组颗粒，剔除针状、扁平状颗粒，每个粒组选取40颗几何形状相似的颗粒并将其浸泡48 h.在加载前，通过多次投放，选用颗粒稳定状态中竖直高度最短的放置方式，将其置于仪器底部加载板上；缓慢下移上加载板，使其与颗粒顶部接触.加载速率为1 mm/min，保证准静态加载，当荷载明显降低且颗粒发生整体破碎时停止加载，破碎前、后的颗粒如图1所示.颗粒在一对加载板挤压下主要为劈裂破坏，可以用下式近似表征颗粒破碎强度[24]：

式中：Ff为颗粒破坏时的轴向荷载，d为颗粒粒径.

对一组有限数量的颗粒开展单颗粒强度试验，不破碎概率Ps可由下式求得：

式中：N为试验颗粒的数量，N(σ ≤ σf)为该组颗粒在压力σ下未破坏的颗粒数.

Ovalle等[24-26]的研究表明，堆石颗粒的破碎强度服从Weibull分布：

式中：m为Weibull模量，反映颗粒强度的离散程度；特征强度σ0为Ps= 37%时的破碎强度.改写式（3），可得

可见，σf与Ps在双对数坐标系下呈线性关系，直线斜率为m；σ0可以通过直线的截距得到.

如图2所示为本次试验颗粒破碎强度的统计结果.图中，大部分点均在拟合线附近，说明Weibull分布能够较好地描述不同粒组玄武岩颗粒的破碎强度.计算各粒组颗粒的m和σ0，结果列于表1.表中，davg为各粒组的平均粒径.可知，不同粒组颗粒的m为2.305～2.835.Ovalle等[24-26]指出粒径对m的影响较小，将不同粒组颗粒m的平均值视为该材料的Weibull模量.选择平均值mavg= 2.541作为玄武岩颗粒的Weibull模量，用于DEM模拟.如图3所示为表1中颗粒特征强度与粒径的关系.可知，颗粒特征强度随着粒径的增加而降低，这可以解释为粒径越大，堆石颗粒内部含有缺陷的可能性越大[24].参考Wang等[26]的研究，采用下式描述玄武岩颗粒特征强度的尺寸效应：

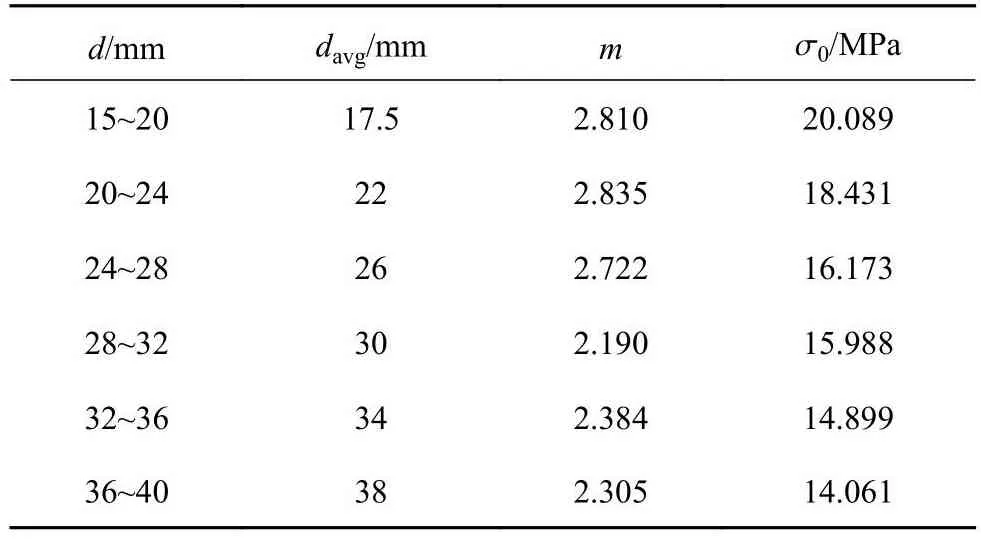
表1 Weibull 拟合参数Tab.1 Weibull fitting parameters

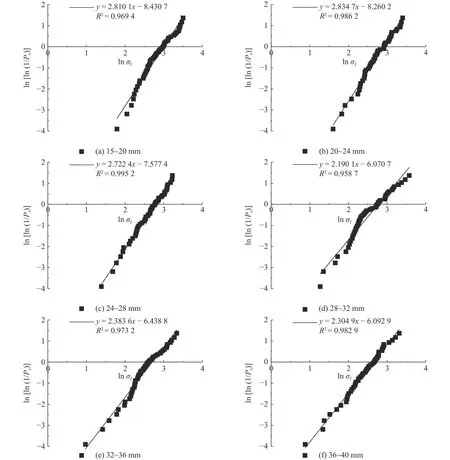
图2 玄武岩颗粒强度与不破碎概率的关系Fig.2 Relation between strength and survival probability for basalt particles

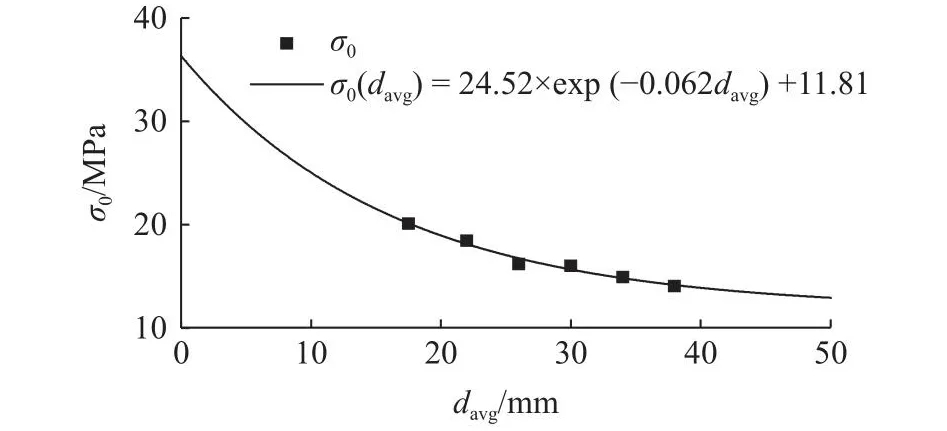
图3 玄武岩颗粒特征强度与粒径的关系Fig.3 Characteristic strength as function of particle size for basalt particles

式中：a、b和c为拟合参数.当davg→0时，σ0(0) =a+c；当davg→∞时，σ0(∞) =c.从图3可见，利用式（5）能够描述粒径对玄武岩颗粒特征强度的影响.拟合参数如下：a= 24.52 MPa，b= 0.062，c= 11.81 MPa.

2 数值试验

2.1 颗粒破碎模拟方法

利用DEM模拟颗粒破碎主要有黏结颗粒法（bonded-particle method，BPM）和碎片替代法（fragment replacement method，FRM）.BPM破碎程度有限且主要用于小规模的数值计算，FRM能够结合室内试验开展较大规模的数值模拟.采用FRM模拟颗粒破碎，而该方法须考虑颗粒破碎准则和碎片替换模式这2个主要问题.Russell等[27]认为集合体中颗粒破碎与否主要受最大接触力控制.本研究基于最大接触力破碎准则模拟单个颗粒的破碎，当粒径为d的颗粒满足下式时发生破碎：

式中：F1，F2，······，Fn为作用在颗粒上的力.破碎临界力Fcrit通过下式[26]求得:

室内单颗粒破碎试验表明，玄武岩颗粒的破碎强度服从Weibull分布.由式（3）可得

进一步联立式(5)、（7）和（8），可得

DEM模拟中，颗粒的Fcrit通过式（9）随机赋值，其中Ps为（0，1.0）区间内均匀分布的随机数，a、b、c和m采用室内试验结果.Ciantia等[28]对比5种Apollonian排列碎片替换模式对颗粒集合体侧限压缩试验的影响，发现采用14个球替换母球（见图4）模拟颗粒破碎，既能够准确反映颗粒材料的力学响应，又能够保证计算效率.本文采用该碎片替换模式.

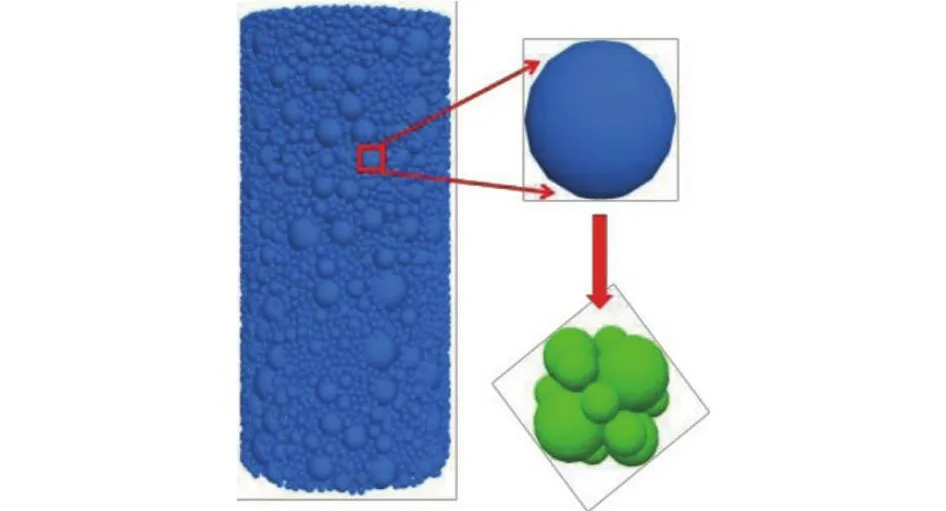
图4 颗粒破碎的替换机制[28]Fig.4 Replacement mechanism for particle crushing[28]

2.2 三轴压缩试验

采用离散元软件PFC3D[29]开展常规三轴压缩试验，选用滚动阻力接触模型考虑颗粒形状的影响.目前，在堆石坝施工中，通过调整爆破参数，使得粗粒料的级配尽量符合Talbot级配方程：wB=100(d/dmax)n，其中wB为小于某颗粒粒径d的质量分数，dmax为最大粒径，n为级配指数.朱晟等[30]调查了我国5座200 m级大坝现场堆石料的坑检资料，发现堆石料级配均较好地服从Talbot级配方程.参照水布垭和三板溪堆石坝中的建议值(n=0.45)确定现场设计级配，利用相似级配法缩尺得到室内级配.在DEM模拟中，通常截断级配，避免小颗粒引起的颗粒数量和计算成本的大幅增加[4-5].张宜等[31]研究不同截断粒径对试验结果精度的影响，指出截断粒径取15 mm对宏观强度和变形特性的影响可以接受.本文选取截断粒径为10 mm，粒径小于10 mm的颗粒，按相同质量等效为10 mm颗粒.级配曲线如图5所示.

借鉴Jiang等[32]提出的分层欠压法，分6层制备试样，详细过程参见文献[26].制样过程不允许颗粒破碎，固结和剪切阶段允许颗粒破碎.为了减少计算成本，在模拟过程中，轴向应变每增加0.01%，开始遍历所有颗粒，调用基于fish语言编写的颗粒破碎替换程序，对将要发生破碎的颗粒进行替换.在试样直径为300 mm,高度为600 mm，围压为2 000 kPa的条件下，比较5种不同的限定粒径dlimit对结果的影响，如图6所示.图中，σ1-σ3为偏应力，εa为轴向应变，εv为体积应变.可见，当使用小于5 mm的粒径作为dlimit时，应力-应变曲线均表现出收敛的结果，可以忽略dlimit的影响.设定dlimit为5 mm，即粒径小于5 mm的颗粒不再进一步破碎.采用正交-等值线法[26]标定玄武岩室内三轴试验[11]，得到一组合适的细观参数.模拟与室内试验的对比结果如图7所示.可见，模拟得到的曲线变化趋势与室内试验结果整体上具有较好的一致性，可以认为该组参数能够用于模拟堆石料的力学特性.如表2所示为DEM模拟参数.表中，ρ为密度，e0为初始孔隙比，E*为有效模量，kr为法向与切向刚度比，µr为滚动阻力系数，µ为摩擦系数.

表2 DEM模拟参数Tab.2 DEM parameters

图6 不同破碎限定粒径下的应力-应变曲线Fig.6 Stress-strain curves for different fracture limit sizes

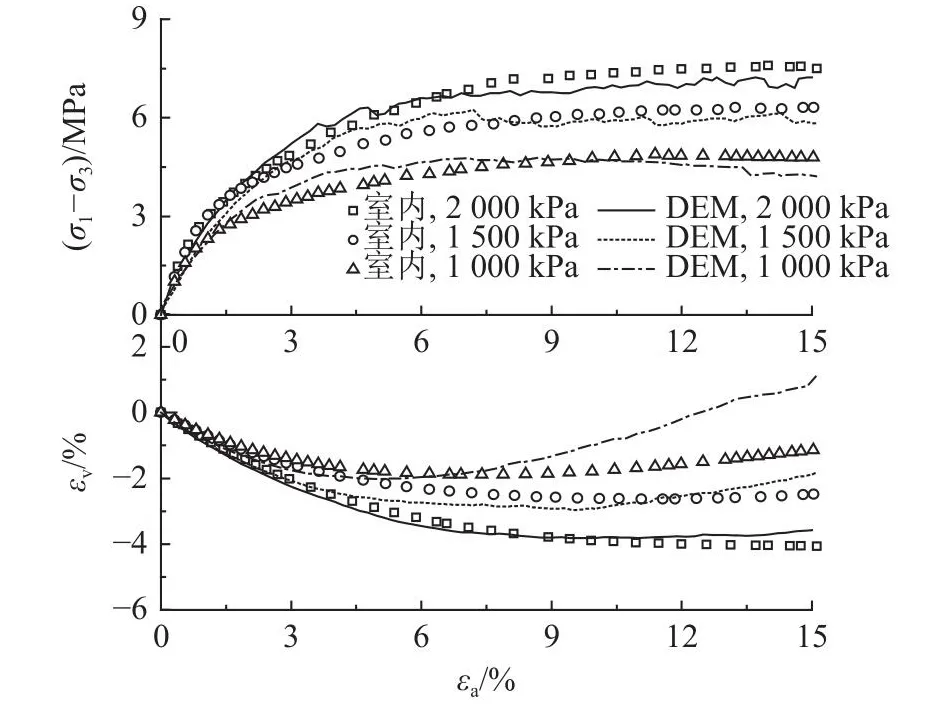
图7 玄武岩堆石料DEM结果与室内试验的对比Fig.7 Comparison between DEM results and laboratory tests of basalt rockfill materials

采用6组试样，研究试样尺寸对堆石料力学行为的影响.如图8所示，三轴试样尺寸（直径D×高度H）从120 mm×240 mm增加到420 mm×840 mm，对应的Rd（D/dmax）从2增加到7.试样包含的颗粒数从1 167增加到50 125.为了考虑颗粒排列的影响，对于每种尺寸，通过设置不同的随机数，制备20个颗粒排列不同的试样.每个试样均考虑500、1 000、1 500和2 000 kPa 4个围压，因此共开展480次三轴压缩试验.

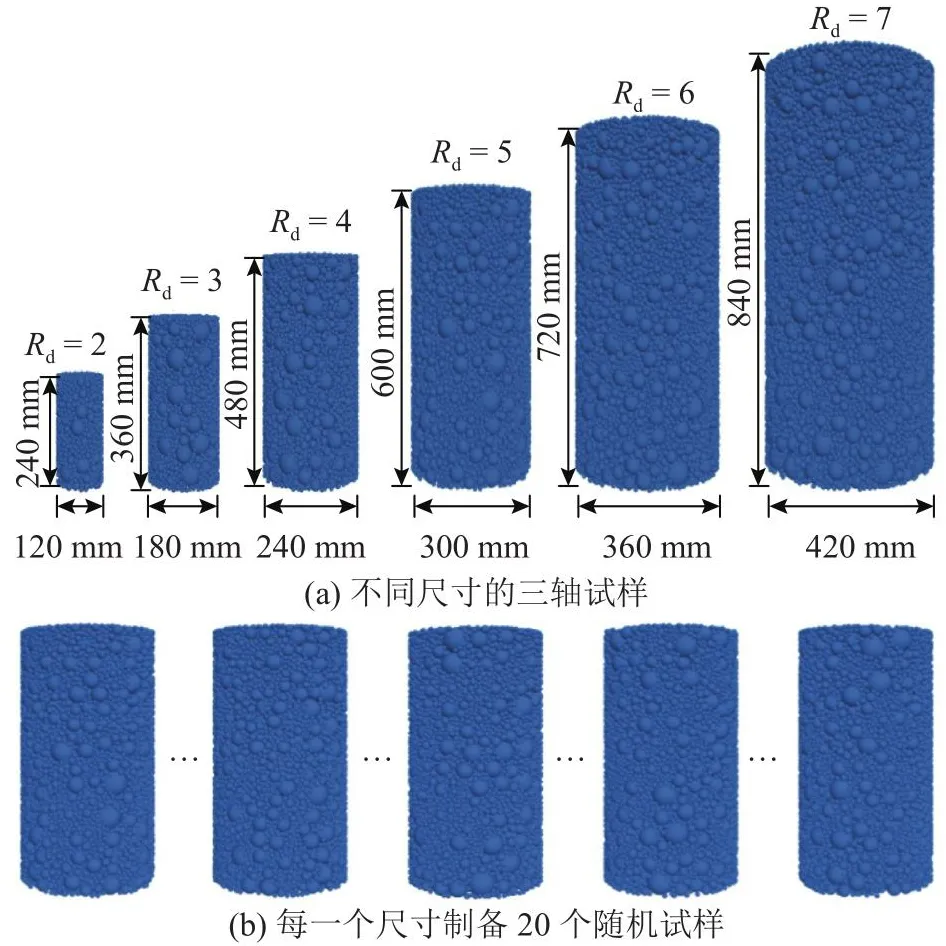
图8 不同尺寸和颗粒排列试样的示意图Fig.8 Schematic diagram of numerical specimens with different sizes and particle arrangements

3 结果与分析

3.1 应力-应变曲线

如图9所示为不同尺寸试样在围压σ3= 2 000 kPa下的应力-应变曲线.可见，当试样尺寸较小时，20个随机试样的应力-应变曲线比较分散，但随着试样尺寸的增加，曲线趋于一致，说明颗粒排列方式影响玄武岩堆石料的力学行为，影响程度与试样尺寸有关.在其他围压下，颗粒排列和试样尺寸对应力-应变曲线的影响规律与围压为2 000 kPa时类似，限于篇幅不再列出.分析试样尺寸对峰值强度(σ1-σ3)f、割线模量E50、泊松比ν、最大体积压缩应变εvmax的影响，如图10所示.由于高土石坝堆石区的应力水平大部分低于50%，选用50%峰值偏应力对应的E50和ν，即

图9 2 000 kPa围压下不同尺寸和颗粒排列试样的应力-应变曲线Fig.9 Stress-strain curves for specimens of different sizes and particle arrangements at confining pressure of 2 000 kPa

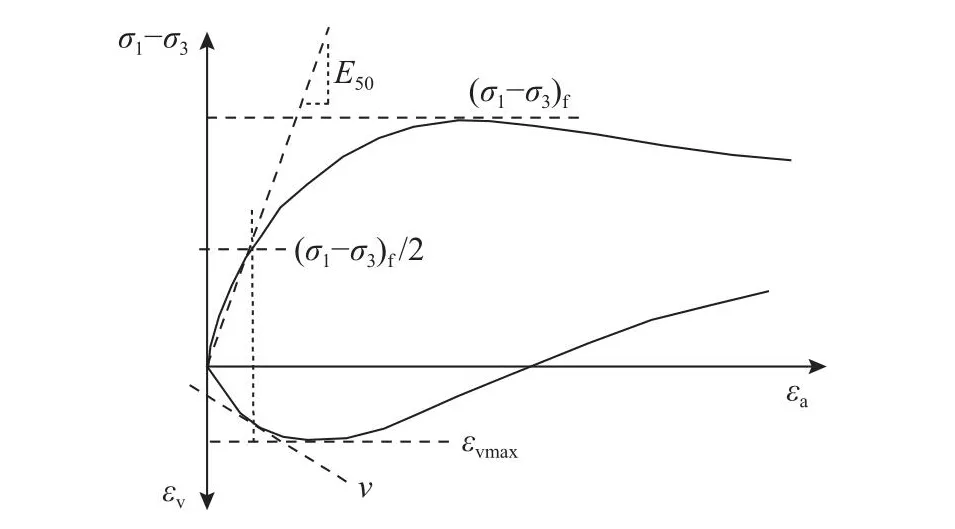
图10 堆石料常规三轴剪切试验的典型轴变-应力-体变关系Fig.10 Stress-strain-volume relation of rockfill materials in conventional triaxial test

式中：ε50%为50%峰值偏应力点对应的轴向应变，εr为径向应变.

3.2 强度参数的表征单元体积分析

根据模拟结果，整理试样在不同工况下的(σ1-σ3)f，即偏应力-轴变曲线上的峰值偏应力.对于没有明显峰值偏应力的曲线，取15%轴变对应的偏应力.如图11（a）所示为试样尺寸对(σ1-σ3)f的影响.实心点为每个尺寸下20个随机试样(σ1-σ3)f的平均值，误差条代表±1倍标准差.从图11（a）可知，(σ1-σ3)f的平均值随着围压的增大而增大，且每个围压下随试样尺寸的变化规律类似，即随着试样尺寸的增加，(σ1-σ3)f的平均值先减小，然后在一定尺寸后变得稳定.另外，反映(σ1-σ3)f离散性的标准差随着试样尺寸的增大而减小.为了减小主观评判误差，采用标准差与平均值的比值（即变异系数CV）确定REV的尺寸.不同围压下峰值强度的CV与试样尺寸的关系如图11（b）所示.在σ3= 500 kPa的条件下，当Rd= 2增大到Rd=7时，峰值强度的CV从大约10.62%下降到1.79%.由于CV = 0仅在理论上可行，在工程应用中通常采用可接受的CV，以确定REV的尺寸.从图11（b）可知，对于σ3= 500 kPa，当Rd= 4时峰值强度的CV开始小于5%，并且从图11（a）可知，峰值强度在Rd= 4时变得稳定.若峰值强度可接受的CV为5%，则当σ3= 500 kPa时，峰值强度的REV尺寸为Rd= 4.分析当围压为1 000、1 500和2 000 kPa时的结果，发现其他围压下峰值强度的REV均为Rd= 4.

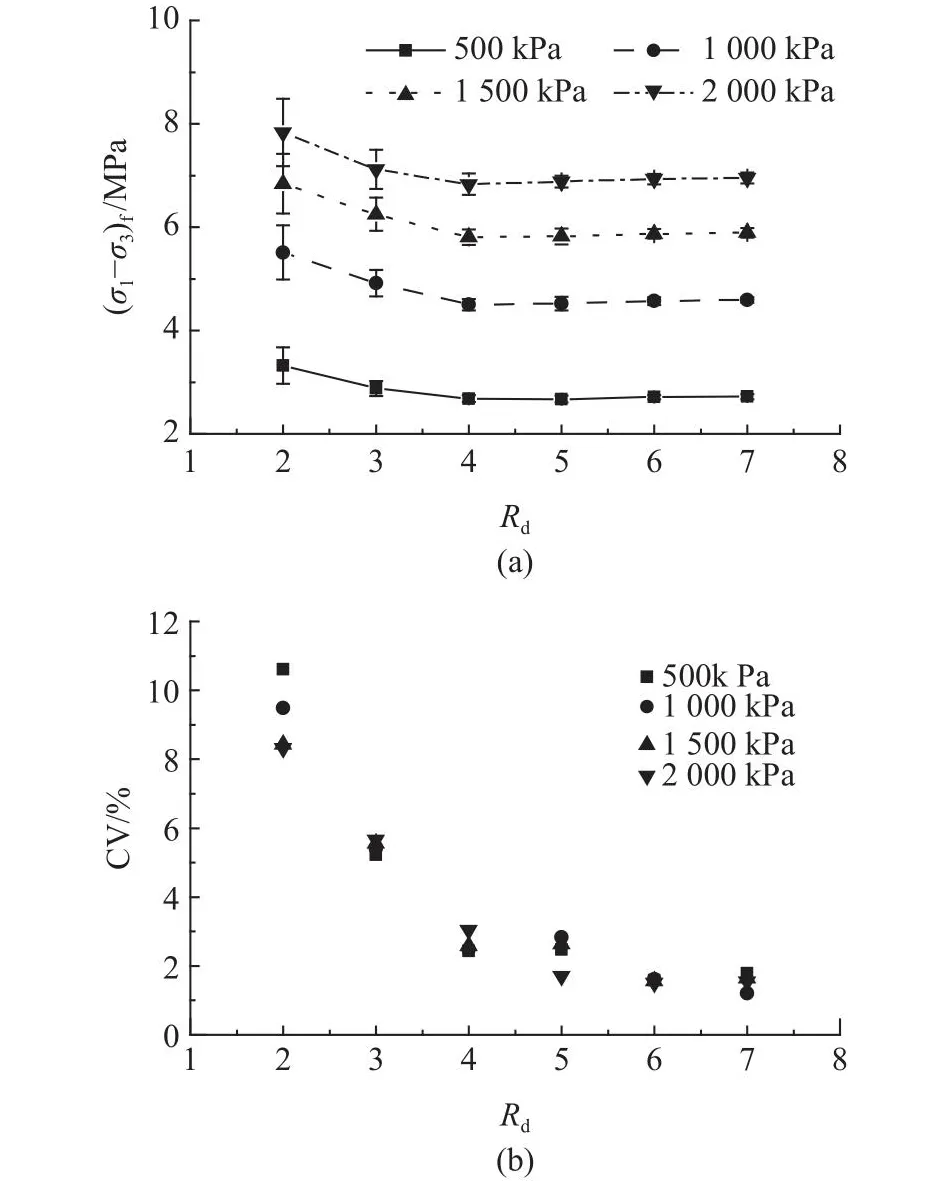
图11 峰值强度及其变异系数随试样尺寸的变化Fig.11 Evolution of peak strength and its coefficient of variation with specimen size

采用邓肯非线性强度理论，分析堆石料强度特性：

式中：pa为大气压；φ0和Δφ为模型参数；φf为峰值摩擦角，

利用式（12）计算试样尺寸和颗粒排列相同的试样在不同围压下的φf，通过式（11）得到该试样的φ0和Δφ.如图12所示为所有试样φ0和Δφ的统计结果.可见，颗粒排列和试样尺寸对φ0和Δφ均有影响，当试样尺寸较小时，φ0和Δφ的数值变化较大，随着试样尺寸的增加，变化幅度逐渐减小.φ0和Δφ相互不独立，即共同反映材料的峰值强度，故它们的REV应相同且须同时满足φ0和Δφ.当Rd= 4时，峰值强度的CV小于5%，而φ0和Δφ的CV分别为1.63%和7.32%，说明峰值强度的REV不适合作为φ0和Δφ的REV.从图12可知，当Rd= 5时，φ0和Δφ的CV均小于5%，φ0为[54.13°，56.62°]，Δφ为[11.37°，12.98°].若φ0和Δφ可接受的CV为5%，则它们的REV尺寸为Rd= 5.

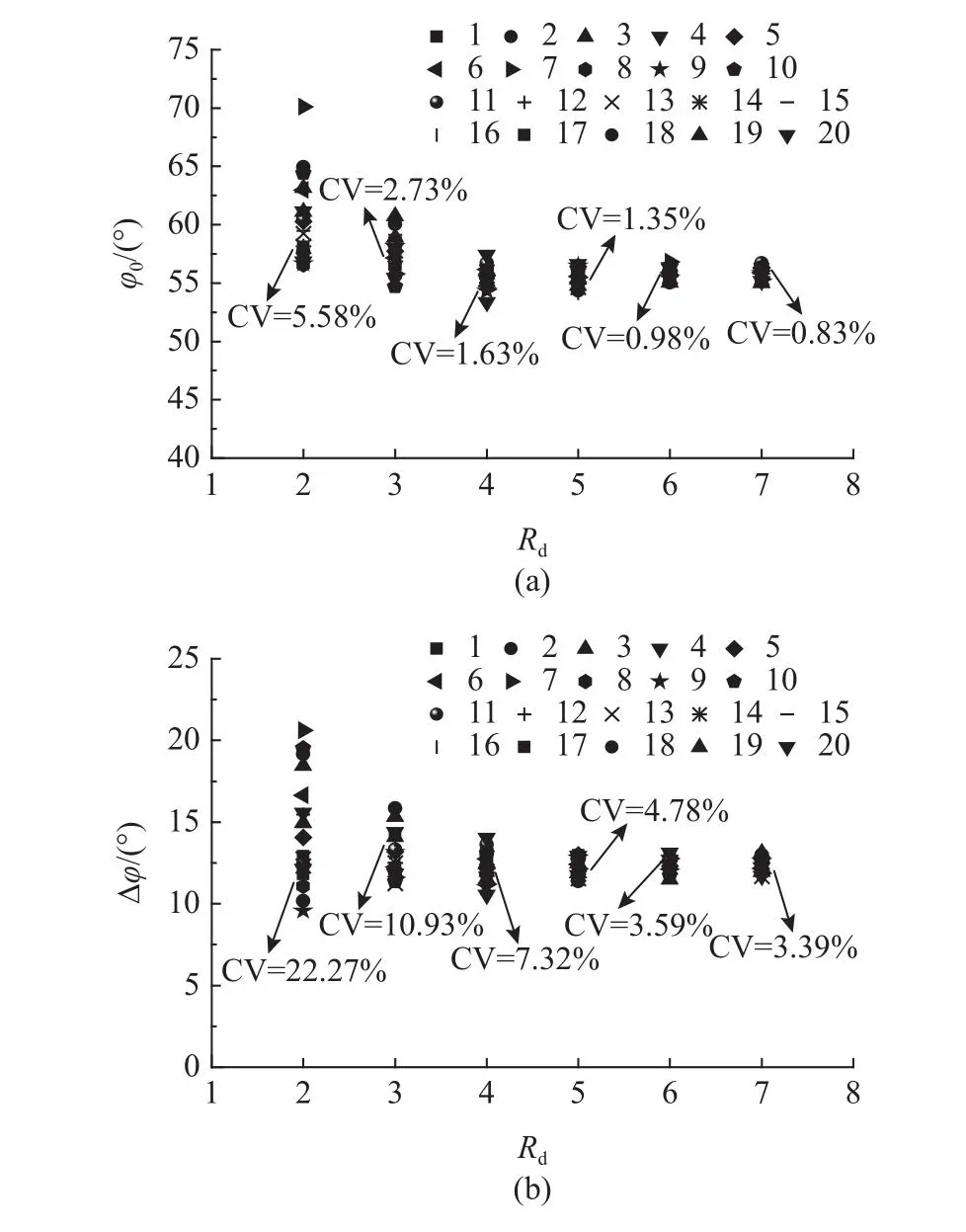
图12 φ0和Δφ的统计结果Fig.12 Statistical results of φ0和Δφ

3.3 变形参数的表征单元体积分析

如图13所示为不同围压下E50及其CV随试样尺寸的变化规律，给出E50的平均值和±1倍标准差.从图13（a）可见，E50的平均值随围压的增大而增大，随试样尺寸的增加而减少，并在一定尺寸后变得稳定.E50的标准差随试样尺寸的增加而减小.从图13（b）可知，E50的CV随试样尺寸的增加而减少.当σ3= 500 kPa时，试样尺寸从Rd= 2增大到Rd= 7，E50的CV大约从8.78%下降到2.96%.当Rd= 4时E50的CV开始小于5%，且E50在Rd= 4时也变得稳定（见图13（a））.若可接受CV为5%，则σ3= 500 kPa下，E50的REV尺寸为Rd= 4.利用同样方法得到在围压为1 000和1 500 kPa的条件下E50的REV均为Rd= 4，而在围压为2 000 kPa的条件下E50的REV为Rd= 5.

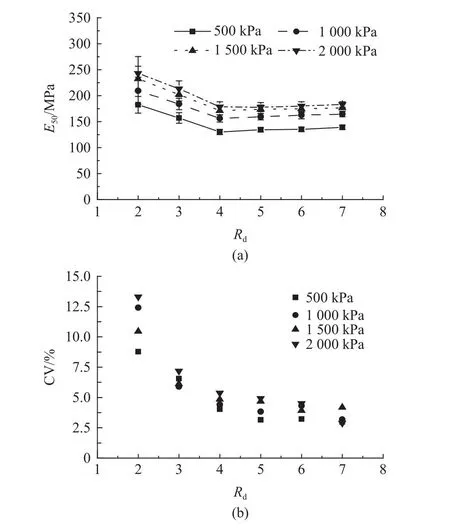
图13 割线模量及其变异系数随试样尺寸的变化Fig.13 Evolution of secant modulus and its coefficient of variation with specimen size

如图14所示为不同围压下，ν及其CV随试样尺寸的变化规律.图中，实心点为ν的平均值，误差条表示±1的标准差.可见，ν的平均值随着围压的增大而减小，随着试样尺寸的增加而降低，但整体变化不大.ν的标准差和变异系数均随着试样尺寸的增加而减少.当σ3= 500 kPa时，Rd从2增大到7，ν的CV大约从13.93%下降到2.18%.若可接受CV为5%，则在σ3= 500 kPa的条件下，ν的REV为Rd= 4.利用同样方法，可得当σ3=1 000 kPa时ν的REV为Rd= 4，当σ3= 1 500、2000 kPa时ν的REV为Rd= 5.如图15所示为不同围压下最大体积压缩应变εvmax及其CV随试样尺寸的变化规律.εvmax的平均值随围压的增大而增大，随试样尺寸的增加而增大，并在一定尺寸后趋于稳定，但当围压较低时平均值整体上变化较小.εvmax的标准差和变异系数均随着试样尺寸的增加而减小.采用CV为5%的标准，可得当σ3=500、1 000 kPa时εvmax的REV为Rd= 4，当σ3=1 500、2 000 kPa时εvmax的REV为Rd= 5.

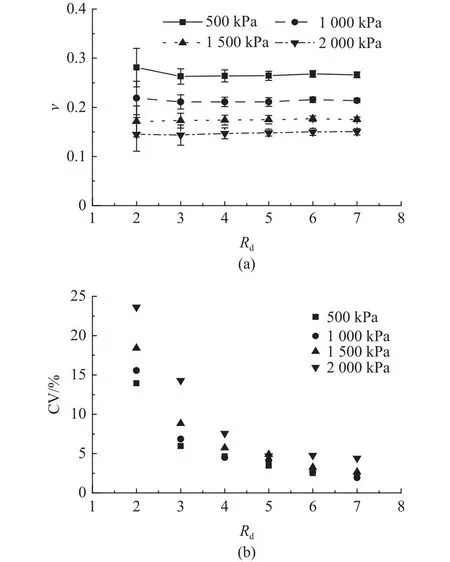
图14 泊松比及其变异系数随试样尺寸的变化Fig.14 Evolution of Poisson ratio and its coefficient of variation with specimen size

图15 最大体积压缩应变及其变异系数随试样尺寸的变化Fig.15 Evolution of maximum volumetric compressive strain and its coefficient of variation with specimen size

3.4 结果讨论

在分析试样尺寸对各强度和变形参数影响规律的基础上，基于CV = 5%标准确定各参数的REV，发现在500、1 000、1 500和2 000 kPa围压下(σ1-σ3)f的REV相同，但φ0和Δφ的REV大于(σ1-σ3)f的REV.这主要是因为当Rd= 4时，颗粒排列不同的试样在相同围压下的(σ1-σ3)f不完全相同，仅是CV小于5%；从式（11）可知，φ0和Δφ由不同围压下的(σ1-σ3)f共同决定，故需要比(σ1-σ3)f的REV更大的尺寸才能使φ0和Δφ达到稳定.通过对比发现，变形参数E50、ν和εvmax的CV基本大于(σ1-σ3)f的CV，说明变形参数对试样尺寸和颗粒排列更加敏感.不同于(σ1-σ3)f，变形参数E50、ν和εvmax的REV在文中的研究围压下不完全相同.2 000 kPa围压下E50的REV大于其他围压下E50的REV.这可能是因为加载过程中颗粒发生破碎引起试样内部颗粒调整，进而影响试样的E50.围压越大，颗粒越容易破碎，加剧了20个颗粒排列不同试样E50的离散性，所以当围压为2 000 kPa时需要更大的尺寸才能获得稳定的E50.同样的原因导致1 500和2 000 kPa围压下ν和εvmax的REV大于500和1 000 kPa围压下相应参数的REV.当Rd= 5时，上述强度和变形参数的变异性均小于5%，说明当Rd= 5时，所有参数的DEM模拟结果均可以达到稳定，这与规范GB/T 50123[17]建议室内三轴试验的试样尺寸（Rd≥5）一致.

4 结 论

(1)室内单颗粒破碎试验表明，Weibull分布可以较好地描述玄武岩颗粒的破碎强度.粒径对Weibull模量m的影响较小，粒径为15～40 mm的颗粒的m为2.305～2.835.玄武岩颗粒的特征强度具有明显的尺寸效应，利用指数函数能够较好地描述粒径与颗粒特征强度的关系.

(2)玄武岩三轴压缩DEM试验表明，颗粒的排列方式影响力学行为，影响程度与试样尺寸有关.峰值强度、割线模量的平均值基本上随着试样尺寸的增加而减少，在一定尺寸后趋于稳定.泊松比、最大体积压缩应变的平均值受试样尺寸的影响相对较小.所有参数的变异系数均随着试样尺寸的增大而减小.

(3)采用5%的可接受变异系数评估各力学参数的REV，发现(σ1- σ3)f的REV为Rd= 4，φ0和Δφ的REV为Rd= 5.变形参数E50、ν和εvmax的REV与围压有关.各参数的REV尺寸不同，因此根据研究对象选择合适的尺寸可以提高计算效率.在本文工况下，所有参数的DEM结果均达到稳定需要的试样尺寸为直径300 mm×高度600 mm（对应Rd= 5），与规范GB/T 50123[17]建议室内三轴试验的试样尺寸（Rd≥ 5）一致.

本研究仅基于特定的工况.Gu等[22]对均一粒径无黏性土开展三轴剪切数值试验，发现当Rd超过11.5后变形模量趋于稳定.这远大于本文级配下E50稳定时需要的Rd，说明级配影响参数的表征单元体积.为了提高计算效率，本文模拟采用滚动阻力考虑颗粒形状的影响.后续将论证本文结论对不同级配及形状不规则颗粒的适用性和误差，重点寻求原型级配堆石料力学参数的表征单元体积.