新型高强硅酸盐墙板钢框架抗震性能

谢国庆，王密，孔德文

(1.贵州大学 土木工程学院，贵州 贵阳 550025；2.中南大学 土木工程学院，湖南 长沙 410083)

随着我国建筑工业化的推进和社会经济发展需求的增长，钢结构由于其施工便捷、自重轻的优点得到了广泛应用[1-2].在结构设计中，填充墙仅被当作非结构构件，不参与抗震计算，仅考虑作为梁上线荷载[3-4].实际上，填充墙与钢框架间通过有效方式连接，能够参与结构抗震[5].Zhang等[6-8]的研究表明，填充墙对结构的承载能力和侧向刚度有一定程度上的提高.

新型高强硅酸盐墙板由贵州省盘江煤电建设工程有限公司用粉煤灰、水泥、纸纤维等经真空挤压、蒸压养护制作而成，具有轻质、高强的优点[9].将粉煤灰应用在建筑材料上的研究有很多[10-14]，大多集中在物理力学性能的研究上，将粉煤灰掺入到预制墙板的研究很少，国内外学者对在地震荷载作用下的墙体-钢框架结构进行大量的研究.Li等[15]提出钢木混合结构的综合抗震性能评估系统.Wang等[16-17]对采用ALC墙板的钢框架结构进行多次抗震性能试验.Ishida等[18]对带有轻钢隔墙和蒸压轻质混凝土墙的足尺钢抗弯框架进行循环荷载试验，评估结构的抗震性能.Cao等[19-20]分别对单层单跨足尺钢框架结构进行抗震性能试验.Bai等[21]提出钢框架墙板构件的内力分布规律.以上文献主要集中在研究不同形式下钢框架结构的抗震性能，而对新型高强硅酸盐墙板钢框架结构的研究则罕见报道.

为了完成新型高强硅酸盐墙板钢框架结构体系在贵州盘江煤电多种经营开发有限公司办公楼项目中的应用与示范，开展1榀空钢框架和1榀内嵌新型高强硅酸盐墙板钢框架结构的拟静力试验，研究钢框架结构的抗震性能、墙体破坏特征.通过有限元软件对结构进行参数化分析，为新型高强硅酸盐墙板的工程应用提供一定的参考依据.

1 试验概况

1.1 试件设计

设计2榀足尺钢框架结构，编号为KJ-1和KJ-2.KJ-1为空框架试件，KJ-2为内嵌新型高强硅酸盐墙板钢框架试件，墙板编号从左到右为板1～5.框架跨度为3 000 mm，层高为2 244 mm，两框架的跨度和层高均相同，如图1（a）所示.墙板尺寸为2 000 mm×600 mm×64 mm，与主体框架间用U型卡件柔性连接，墙板的详细尺寸如图1（b）所示.框架柱采用方形钢管，横截面尺寸为200 mm×200 mm×10 mm，梁采用H型钢，横截面尺寸为HM244 mm×175 mm×7 mm×11 mm.试件所用的钢材均为Q235级钢，梁柱节点用外隔板连接、栓焊固定.试件的制作流程如图1（c）所示.板缝用砂浆抹平，墙板与框架间缝隙用GB-SR柔性填料填充，用于保护墙体与框架硬接触破坏.为了便于在框架内安装墙体，安装时在墙板底部放置丙烯废水管，便于墙体安装.

1.2 材性试验

试验所用的新型高强硅酸盐墙板质量配合比如下:m(水泥)∶m(粉煤灰)∶m(细砂)∶m(纸纤维) =23.76∶29.10∶47.10∶0.04.根据《建筑隔墙用轻质条板通用技术要求(JG/T 169-2016)》[22]，测得新型高强硅酸盐墙板的抗压强度为40 MPa，泊松比为0.2，弹性模量为11 000 MPa[9].为了测试钢材的力学性能，根据规范GB/T 228.1—2010和GB/T 2975—2018[23-24]，对钢框架梁、柱、连接板等重要部位取样并进行拉伸试验，共计12个试样.试样均从母材中切取，与试验中的试件为同期加工钢材.采用电子万能拉伸试验机进行拉伸试验，变形由YSJ-100电子应变仪测量，计算得到屈服强度、极限强度、弹性模量和泊松比等重要参数.材性试验装置和结果分别如图2和表1所示.表中，fy为屈服强度，fu为极限强度，Es为弹性模量，γ为泊松比.

表1 钢材材性的试验结果Tab.1 Test results of steel material property

图2 钢材材性试验装置Fig.2 Steel material property test device

1.3 加载装置及加载制度

在贵州大学土木工程学院结构工程省级重点实验室中开展试验.由于试验条件所致，仅在立柱顶端施加由美国MTS液压伺服加载系统提供的水平低周往复荷载，该仪器最大行程为±250 mm.在钢梁两端放置连接板，用4根钢棒连接.在关键位置布置位移传感器和应变片，数据由JM3813多功能静态应变片装置采集，测点布置和加载装置分别如图3、4所示.

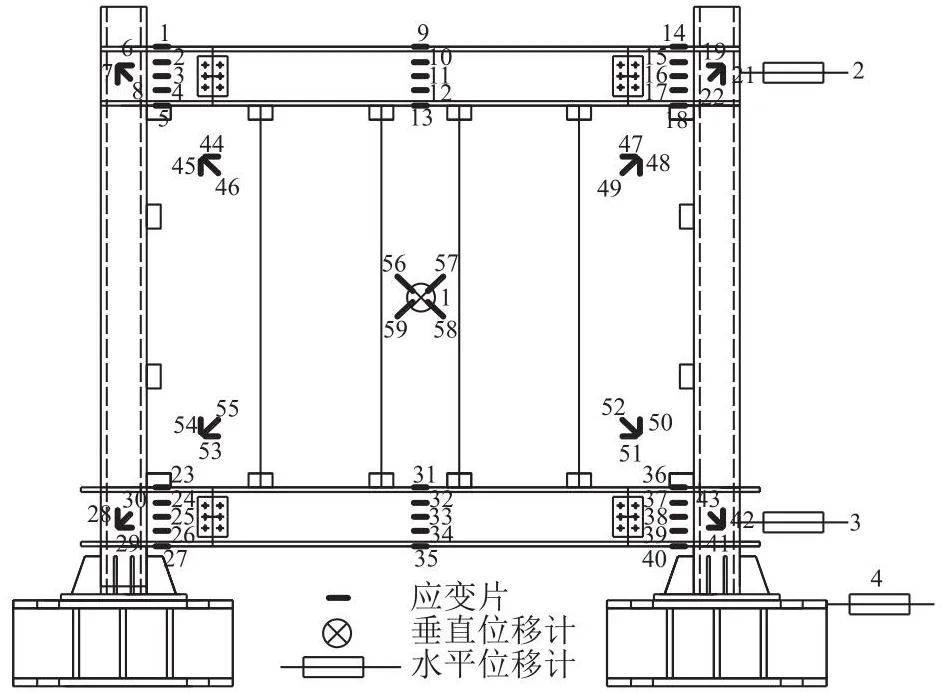
图3 试件测点布置的示意图Fig.3 Schematic diagrams of measuring points arrangement of specimen

图4 试验加载装置Fig.4 Test loading device

根据《建筑抗震试验方法规程》 （JGJ/T 101—2015）[25]，采用荷载-位移控制的方式加载.加载过程分为以下3个阶段：1）预加载，检测仪器是否正常工作；2）荷载控制，加载至试件屈服；3）位移控制，加载至试验结束.具体的加载方式如下.

KJ-1.在荷载控制阶段，初始荷载为20 kN，以20 kN为级差，每级循环一次加载，当荷载达到140 kN时，减少级差为10 kN，并以该级差加载至结构屈服.屈服后，采用位移控制加载，并以屈服位移的整数倍依次增加，每级循环3次，直至结构发生严重变形，认为试件不宜继续加载，停止试验.

KJ-2.在荷载控制阶段，初始荷载为5 kN，加载至20 kN，以20 kN为级差加载至试件屈服.每级循环一次，直至试件屈服，改为位移控制加载，并以屈服位移的倍数为级差进行加载.每级循环3次，直至墙板严重破坏，则停止试验.

2 试验现象及破坏形态

2.1 KJ-1破坏过程

在力控制阶段的初期，未见明显形变.当荷载增加到+100 kN时，试件发出轻微细小的咔嚓声.当加载到+140 kN时，外隔板和柱脚应变接近屈服应变，表明梁端和柱底即将进入局部屈服.当荷载达到+170 kN时，外隔板和柱脚已经屈服，此时梁端位移为26 mm，当位移回归至零时改为位移控制加载.当位移增加至+78 mm时，左侧上节点外隔板上翼缘屈曲，如图5（a）所示.继续增加位移，当位移达到+92 mm时，右侧上节点下翼缘焊缝断裂，并伴随着连续的响声.当位移增加至130 mm时，结构的承载能力下降，为了保证试验的安全，在位移回归至零点后，停止加载试验.

图5 KJ-1试验现象[26]Fig.5 Test phenomenon of specimen of KJ-1

2.2 KJ-2破坏过程

当荷载增加至-15 kN时，板4和板5间的嵌缝砂浆出现竖向细微裂纹，宽度为1.52 mm，如图6(a)所示.当荷载增加到80 kN时，右边上部GB柔性填料被挤出.当荷载达到180 kN时，面板产生首条裂纹，当继续增加至200 kN时，结构屈服，此时位移为29 mm.改为位移控制加载，当位移增加至-58 mm时，墙体整体翘起，左侧上节点外隔板屈曲，板2面板的局部表皮脱落，如图6(b)、(c)所示.当加载至87 mm时，右柱上部钢梁外隔板屈曲，板4出现竖向斜裂缝并随着荷载的增加而持续增大，且底部混凝土垫层被压溃，如图6(d)～(g)所示.当位移加载至116 m时，板4面板块状剥落，在第2位移循环的-116 mm时，墙板严重破坏，该结构的承载能力下降，为了保证安全，停止加载.

图6 KJ-2试验现象Fig.6 Test phenomenon of specimen of KJ-2

2.3 试验现象的分析

试件的破坏模式主要包括外隔板屈曲、焊缝断裂、墙板间嵌缝砂浆碎裂、墙板破碎等.整体上看，新型高强硅酸盐墙板在整个加载过程中的整体性能较好，未发生裂缝贯穿、墙板断裂的严重破坏现象，填充的GB柔性填料保护了钢框架对墙体产生的直接破坏.由于试件在制作过程中，加工厂采用9 mm的外隔板，导致外隔板严重屈曲，造成了梁节点率先形变.

3 试验结果及分析

3.1 滞回性能

试件的滞回曲线如图7所示.图中，P为荷载，Δ为位移.在加载前期，荷载和位移呈线性增长，此时试件处于弹性阶段，两试件的滞回曲线均呈梭型，且较饱满，体现该结构良好的滞回性能.随着位移的持续增加，残余变形和滞回环面积相应增加，但刚度有所下降，在相同的位移等级下，滞回环面积和结构承载能力都有所下降.滞回曲线出现滑移，原因是上部钢梁在试验过程中发生横向变形，导致加载过程中加载板和框架之间出现间隙.

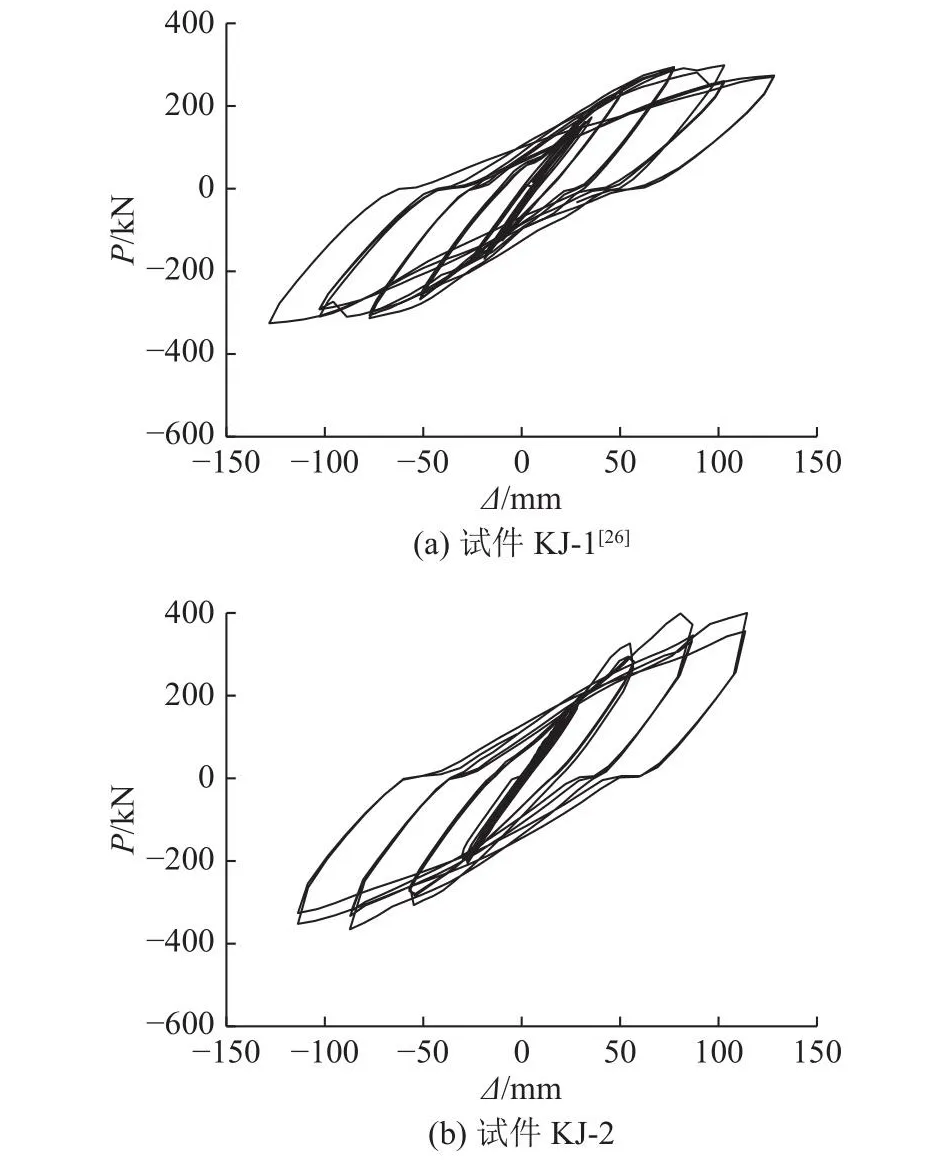
图7 试件的滞回曲线Fig.7 Hysteresis curve of specimens

3.2 骨架曲线和延性

两试件的骨架曲线如图8所示.可知，KJ-2的刚度略大于KJ-1，这是由于在小位移作用下，KJ-2内嵌墙板未能完全参与作用，此时荷载大部分由框架承受.墙板对钢框架的初始刚度影响不大，但对结构的承载能力影响较大，正向加载时KJ-2提高了35.5%，负向加载时提高了22.5%，说明该复合结构在加载初期墙板不参与作用，在加载后期墙板和框架具有很好的协同作用.试件KJ-2在推、拉2个方向的受力性能存在一定的差异，这是由于左上节点梁翼缘率先屈曲，导致左柱刚度下降，形成“强推弱拉”的现象.KJ-2在到达极限荷载后能够保持一定的承载能力，这是因为部分墙板失效后仍有部分墙板能够承受侧向荷载.

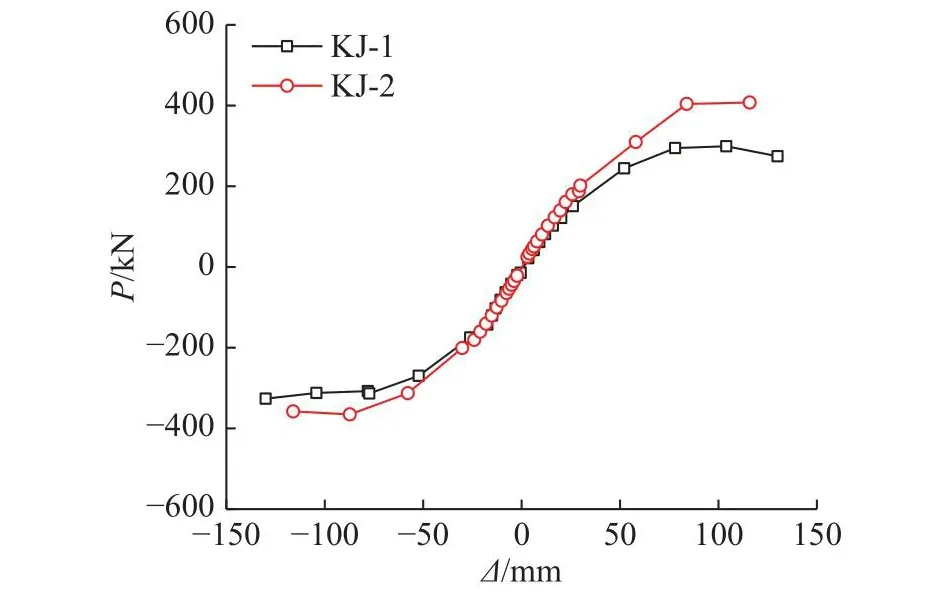
图8 试件骨架曲线的对比Fig.8 Comparison of skeleton curves of specimens

根据JGJ/T101—2015，采用延性系数表示试件的延性特征，得到低周循环加载下试件部分力学性能，如表2所示.表中，Δy为屈服位移，Δu为极限位移，θy为屈服位移角，θu为极限位移角，µ为位移延性系数，µθ为位移角延性系数.从表2可知，两试件的层间位移角均已达到GB 50011—2010中1/50的位移角限值要求，表明两试件均具有良好的变形和承载能力.

表2 低周循环加载下试件的力学性能Tab.2 Mechanical properties of specimens under low cycle loading

3.3 刚度退化

两试件的刚度退化曲线如图9所示.图中，K为刚度.从图9可知，KJ-2的初始刚度比KJ-1大2.2 kN/mm，该安装形式下新型高强硅酸盐墙板对框架的初始刚度有一定的提高.在加载过程中KJ-2的整体刚度比KJ-1大，这是由于墙板参与共同作用，增大了抗侧能力.当荷载增大时，结构的抗侧刚度逐渐下降，是由框架屈曲、墙板开裂所致的.

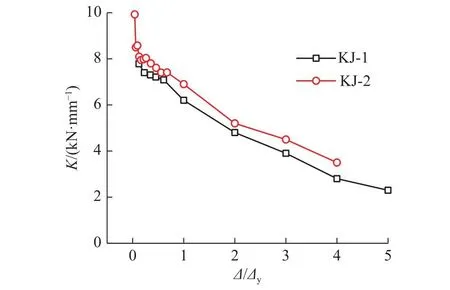
图9 试件刚度退化曲线的对比Fig.9 Comparison of specimen stiffness degradation curve

3.4 耗能能力

采用耗散能量和耗能系数，评价结构的耗能能力.耗散能量为构件在每级荷载-位移曲线对应的最外层滞回环包围的面积SABC+SCDA，耗能系数E=(SABC+SCDA)/(SOEB+SODF)，如图10所示.

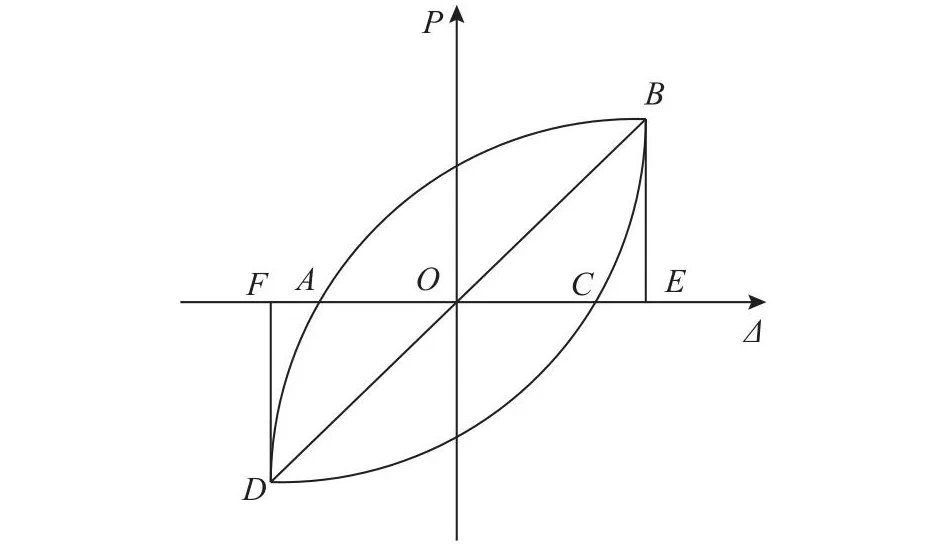
图10 荷载-位移曲线滞回环Fig.10 Hysteresis loop of load-displacement curve

如表3所示为试件在各级加载下的耗能指标.表中，W为耗散能量，E为耗能系数.由表3可知，随着荷载位移的增大，滞回环包络面积不断增加，KJ-2的耗散能量较KJ-1提高了34.19%，表明填充新型高强硅酸盐墙板可以显著提高结构的耗能能力.对比耗能系数可知，两框架均达到1.2，且仍处于上升趋势，两试件在位移控制加载下，都呈增大趋势.在墙板退出工作前，KJ-2由于有框架和墙板协同工作，拥有更出色的耗能能力，但是在墙板发生破坏后主要由钢框架承受荷载.

表3 耗能指标Tab.3 Energy consumption capacity

4 数值模拟

4.1 模型建立

利用有限元分析软件ABAQUS对试验结果进行分析，提出内嵌新型高强硅酸盐墙板钢框架结构的数值模拟方法.钢材和GB柔性填料用S4R壳单元建立，新型高强硅酸盐墙板用实体C3D8R单元建立.钢材本构用三折线模型，GB填料用弹性模型，墙板用混凝土损伤模型[27]，损伤模型中的弹性模量、抗压强度、泊松比等参数根据试验得到.如图11所示为KJ-2的网格模型，KJ-1网格模型把KJ-2中的墙体去掉即可，模拟中施加的荷载和试验一致.

图11 KJ-2网格模型Fig.11 Grid model of KJ-2

4.2 模型验证

如图12所示为两试件有限元和试验滞回曲线的对比.有限元模拟是理想化状态，忽略试件的初始缺陷，如焊缝质量、材料缺陷、安装误差等的影响，导致模拟荷载大于试验的实际情况.从图12可知，模拟曲线在每个位移等级下的荷载提升较快，在加载后期出现荷载下降的情况，主要是由于加载板耦合于一点，上部钢梁变形使得端部产生空隙，刚度减小.

图12 试件的滞回曲线对比Fig.12 Hysteresis curve comparison of specimens

如图13所示为有限元和试验骨架曲线的对比.可知，试验在加载初期，曲线基本吻合.试件与有限元模拟极限荷载的误差小于20%，证明了有限元模拟的合理性和有效性.

图13 试件的骨架曲线对比Fig.13 Comparison of skeleton curves of specimens

4.3 参数分析

4.3.1 高跨比的影响 为了考虑不同高跨比对新型高强硅酸盐墙板钢框架结构抗震性能的影响，框架高度为2 244 mm，通过改变跨度调整高跨比h/l，取值分别为0.50、0.75、1.00和1.25.通过模拟得到的骨架曲线如图14所示.经分析可知，初始刚度最大的试件高跨比为0.75，试件的极限承载能力随着高跨比的增加先增加后减少，并随高跨比的增加有持续下降的趋势.当高跨比较大时，对结构不利；当高跨比较小时，刚度退化较快，建议高跨比取值为0.50～0.75，此时结构的整体受力性能较好.

图14 不同高跨比下试件的骨架曲线对比Fig.14 Comparison of skeleton curve of specimens under different height span ratios

4.3.2 轴压比的影响 通过对框架柱顶施加轴心压力，考虑不同轴压比对新型高强硅酸盐墙板-钢框架结构抗震性能的影响.轴压比µ分别取0.2、0.3、0.4和0.5，模拟得到的骨架曲线如图15所示.经分析可知，随着轴压比的增大，试件的极限荷载下降较明显，且屈服荷载有一定的下降趋势，试件初始刚度的变化不明显.当轴压比为0.5时，结构达到极限荷载后呈下降趋势；当轴压比为0.2～0.4时，结构具有良好的耗能能力，建议轴压比的取值不大于0.4.

图15 不同轴压比下试件的骨架曲线对比Fig.15 Comparison of skeleton curves of specimens under different axial compression ratios

4.3.3 墙板厚度的影响 在KJ-2的基础上改变墙体厚度，研究墙板厚度对钢框架结构抗震性能的影响.墙板厚度取目前实际工程中常用的隔墙厚度δ，分别取60、90和120 mm，如图16所示为不同厚度下结构的骨架曲线.可知，随着墙板厚度的增加，结构的承载能力相应增大，弹性刚度变化不大，极限承载能力较60 mm厚墙板分别提高了8.1%和18.5%.

图16 不同墙体厚度下试件的骨架曲线对比Fig.16 Comparison of skeleton curves of specimens with different wall thicknesses

5 结 论

(1) 破坏模式主要为嵌缝砂浆开裂、墙体面板开裂剥落、梁翼缘屈曲等情况.

(2) 墙板对钢框架的初始刚度影响较小，但KJ-2的承载能力、耗能能力都远高于KJ-1，承载能力正向加载时提高了35.5%，负向加载时提高了22.5%，耗散能量总值增大了34.2%.

(3) 模拟结果表明：试件的承载能力随着高跨比的增加先增后减，建议高跨比取值为0.50～0.75.当轴压比为0.2～0.4时，结构具有良好的耗能能力，建议轴压比取值不大于0.4.改变墙板厚度对结构的初始刚度影响不大，但对结构的极限承载能力有一定程度的提高.