基于多态模糊贝叶斯网络的半潜平台安装风险分析

冯 岩，余建星

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中国交通建设股份有限公司，北京 100088）

随着我国深水油气资源开发进程的加快，半潜式平台作为一种典型的浮式平台具有良好的应用前景，现已有多艘半潜平台在我国南海海域投入使用，服务于深海油气勘探、钻井、完井等生产任务。然而，半潜平台安装作业是一个复杂的系统工程，涉及多工种多设备协同作业，工作环境随时受到复杂多变的海洋环境影响，工程费用高昂，施工工艺流程复杂，需要较高的工程技术水平。在安装作业过程中一旦出现安全事故，将会导致结构设备损伤、工期延误、成本激增甚至人员伤亡。因此，对半潜平台安装作业过程中潜在的风险事件进行预测和分析，预判事故根源，及时采取有效的防控措施降低意外事故发生的风险，具有重要的工程意义。

近年来，国内外学者针对不同工程领域的风险评估开展了广泛的研究工作，形成了多种风险分析方法［1-5］，如故障树分析法（FTA）、失效模式与影响分析（FMEA）、层次分析法（AHP）等。为了解决风险评估所需基础数据欠缺的问题，诸多学者结合模糊理论建立了多种模糊风险分析方法，并在海洋工程安全风险评价方面发挥了重要作用［6-7］，然而在风险反向推理、多源信息融合与表达及动态风险分析等方面依然存在一定的局限性。

贝叶斯网络（BN）方法是以概率论和图论为基础发展起来的概率图模型，能够有效描述不确定性逻辑关系信息，分析处理事件的多态性，实现事故原因与结果的双向推理计算。但受传统概率方法的影响，仍存在基于精确概率进行不确定性推理的局限性［8］。已有学者将模糊集理论（FST）和BN 进行互补融合，形成模糊贝叶斯网络（FBN）方法，并用于风险评估与管理中［9-10］。Cai等［11］提出了一种基于FBN 的水下防喷器安装过程定量风险评估方法，在应用中取得了良好效果。王成汤等［12］综合考虑故障状态的模糊性和系统多态性，提出了一种多态模糊贝叶斯网络（PFBN）方法并成功应用于地铁车站深基坑坍塌可能性评价。然而，在深水半潜式平台安装作业风险评价方面鲜有关于PFBN的研究成果。

PFBN 方法基于领域专家的经验知识计算目标事件的定量发生概率，但是对专家知识获取的可靠性，专家知识转化过程中的模糊数定义，以及去模糊化换算的合理性方面缺乏相关研究。模糊数定义与换算方法不匹配，会导致计算结果与实际情况存在较大偏差［13］，影响评估结果的准确性。并且，在结合工程作业过程动态风险分析方面的应用仍显不足。

因此，构建了一种基于PFBN方法的半潜平台安装作业风险分析模型。基于中国船级社（CCS）推荐的事故概率评估标准，定义了用于描述专家语言性评价的模糊数；采用相似性聚合方法（SAM）结合置信度指标对专家意见进行聚合，反映专家知识的可靠性；引入了改进的去模糊化计算方法，实现了模糊化与去模糊化过程的一致性；基于BN 的双向推理与事件敏感性分析的能力，实现安装全过程风险评估。最后，对陵水17-2项目半潜平台整体吊装作业进行风险分析，为工程风险管理与防控策略制定提供指导。

1 基本理论及概念

1.1 贝叶斯网络

贝叶斯网络是一种基于可视化网络图描述随机事件概率相互关系的方法，可通过二元组来表示。其中G=，表示可视化有向无环图（DAG）。V={X1，X2，…，Xn}为节点的集合，表示随机变量或事件，π(Xi)表示子事件Xi的父集；E为有向边的集合，能够反映随机变量间的逻辑关系。P是条件概率表（CPT），用于描述有向无环图中各个节点事件间的概率影响关系。

假设A为具有ki个状态a1，a2，…，aki的多态变量，则B的发生概率可通过全概率公式得到，如式（1）所示。

BN的联合概率分布，可根据根事件的先验概率和事件间的条件概率计算得到，如式（2）所示。

1.2 模糊集理论

为了解决由数据不完备和不精确引起的不确定性问题，Zadeh［14］提出了FST，认为在实数域的连续区间内，某元素对某集合具有不同的隶属程度，超越了传统集合中“非此即彼”的隶属关系，为描述不确定性提供了新的数学工具。

定义M͂为在论域U中的模糊集，可用式（3）进行表示。

式中：μM͂(x)表示论域中任意元素x对模糊集M͂的隶属度值。隶属度函数有多种形式，其中梯形模糊数和三角形模糊数由于概念清晰、计算简便，在描述定性概念中具有广泛应用。

传统的二态系统仅将事件考虑为“正常（0）”和“失败（1）”两种状态，而实际事件可能有多种状态，传统方法无法客观全面地描述事件可能存在的状态。在安装作业的风险分析中，可分别采用数字0、0.5、1 来表示事件的“正常”“中等故障”和“严重故障”3种状态。

2 基于PFBN的风险分析模型

为解决风险评估中确定性概率难以获取以及风险事件的多态性问题，构建了基于PFBN 的风险分析模型，用于半潜平台安装作业风险分析与安全防控，主要流程如图1所示。

图1 基于PFBN的风险分析流程Fig.1 Risk analysis process based on PFBN

2.1 BN结构构建

首先，将半潜平台安装过程的流程图转化为主贝叶斯网络。然后，确定安装作业不同阶段的BN，建立完整的BN 结构。各阶段BN 结构的直接构建较为复杂，基于故障树（FT）转化的方法构造BN 结构既能够充分利用FT对风险因素识别的能力，又能够结合BN在推理计算方面的诸多优点。因此，采用FT转化为BN的方法来构造不同安装作业阶段的BN结构［15］。

2.2 根事件先验概率及其他事件CPT确定

BN推理分析依赖于对根事件先验概率和其他事件CPT的精确求解，因缺乏实际的统计数据而无法精确获得事件各状态概率的条件下，往往需要通过专家启发和评估的方式借助专家知识和实际经验获得。领域专家基于经验知识做出定性概率判断，无法直接给出精确的定量概率数据，其评估结果不可避免地存在一定的主观性和模糊性。因此，采用一种改进的模糊聚合方法，以确定BN中根事件的先验概率。

2.2.1 专家评判意见模糊化

评价术语反映了专家对事件发生概率的认识，其定义有多种方式［16］。根据行业习惯或规范制定概率分级标准，形成概率评价模糊集合，专家通过评价术语表达观点。风险事件概率分析一般按照风险发生频次进行分级，中国船级社（CCS）发布的指南［17-18］中推荐了海洋平台结构的风险概率等级划分标准，确定了5 个频率等级。据此定义频率等级的评价术语为“非常高（VH）”“高（H）”“中等（M）”“低（L）”“非常低（VL）”5 个变量，用于衡量平台安装作业风险发生的概率。为了描述频率论域内不同数值对于各个评价模糊集的隶属程度，构建了三角形模糊数和梯形模糊数以实现语言变量的定量数学表达，如图2所示。

图2 不同频率等级模糊数Fig.2 Fuzzy numbers for different frequency levels

2.2.2 专家评判意见聚合

为获取综合的评价结果，不同专家的评价值需要进行信息融合。由于教育背景、工作经验和风险态度的差异，以及评估者对个人评判值具有不同的置信程度，评价数据具有不同的可靠性。需要综合考虑专家的客观能力和主观信心，对调查数据进行可靠性评估。因此，使用专家置信度指标，结合相似性聚合法（SAM）［19］对专家模糊意见进行聚合处理，以反映调查数据的可靠性。

一方面，考虑专家的职称、学历、工龄、年龄4个因素，根据文献［20］的方法，计算每位专家的客观能力得分ξ。另一方面，考虑专家的主观信度水平ψ，分为5 个等级，分别为1.0、0.9、0.8、0.7、0.6。ψ越高，判断越可靠。假设有m位专家参与，则第j位专家的置信度指标（用θj表示）可以通过式（4）计算得到。

专家Ej的权重w(Ej)为：

专家Ej(j= 1，2，…，m)对每个评估对象给出评判语义值R͂j，并转换成相应模糊数。两个模糊数之间的相似度S(R͂j，R͂k)、平均一致性A(Ej)、相对一致性测度R(Ej)和一致性系数C(Ej)可由式（6）～（9）获得。

式中：β为松弛因子，通常取值为0.5。专家评判值的综合评价结果为：

2.2.3 去模糊化得先验概率

首先通过最小最大设置法［21］获取模糊可能性分数SFPS，继而通过Onisawa转换公式［22］转化为模糊失效率PFFR，作为根事件先验概率。定义专家评语变量时，采用了CCS 推荐的海洋平台结构风险概率等级划分标准。在去模糊化过程中，需要遵循相同的转换对应关系，而Onisawa转换公式主要用于人机交互系统的失效率计算，与这里定义的概率等级划分标准不一致。因此，采用一种改进的方法［13］实现SFPS至PFFR的转化：

2.2.4 CPT的确定

FT 中的逻辑门可直接转化为BN 中的CPT，但无法对多态系统中的事件关联性进行描述。多态系统中事件的关联性需要更多的条件概率关系。通过专家评判确定不同事件间的条件概率分布。

2.3 BN双向推理及敏感性分析

2.3.1 双向推理

正向因果推理是基于给定的根事件先验概率，以及不同事件之间的条件概率分布，计算出顶事件的发生概率。反向诊断推理是将顶事件发生作为已知条件，通过式（13）计算得出每个事件的后验概率，可用于衡量每个事件对顶事件影响发生的贡献程度。

其中，P(Xi=xj|T= 1)表示顶事件T= 1 发生时，第i个根事件的后验概率。xj表示事件Xi的可能状态，三态事件可取0、0.5和1。后验概率值越大，该事件对顶事件T= 1的贡献程度越大。

2.3.2 敏感性分析

通过对根事件进行敏感性分析，可以判断其对顶事件发生的影响程度，从而识别出关键风险因素。选用RoV重要性度量MRoV［10］来衡量根事件的敏感性程度。根事件Xi的MRoV如式（14）所示。

式中：P(Xi=xj)表示先验概率，P(Xi=xj|T= 1)表示后验概率。ki表示根事件Xi的非0 风险状态个数，若事件状态用0、0.5、1描述，则ki为2。

3 工程实例分析

以陵水17-2工程项目为例，基于构建的PFBN模型，开展深水半潜式平台安装作业风险分析。辨识潜在风险事件，建立BN 结构，通过海洋工程领域专家进行目标事件先验概率评估预测，并开展BN 推理分析，判断事件的敏感性和后验概率，确定关键风险事件，为工程作业安全管理提供参考。

3.1 BN构建

陵水17-2 气田半潜平台安装采用整体吊装法，对平台船体和上部组块结构进行安装，涉及的施工作业主要包括5 个过程，分别为船体与组块拖航运输、组块就位与试吊、船体进坞定位、组块吊装与焊接、平台整体出坞。核心工作任务是将总质量约1.5万t的上部模块通过泰山吊准确吊放在船体上部，精准对接并进行焊接固定。首先建立安装过程流程图，并将流程图转化为主贝叶斯网络，如图3 所示。然后，根据不同的安装阶段，进一步分析潜在的风险事件，构建FT 并转化为BN 结构。最后建立半潜式平台安装风险的完整BN结构，如图4所示。顶事件T表示深水半潜式平台安装失败，中间事件A1～A5、B1～B15、C1～C9及根事件X1～X43所对应的名称如表1和表2所示。事件T和A1～A5为二态事件（“正常（0）”和“失败（1）”），事件B1～B15、C1～C9及所有根事件X1～X43为三态事件（“正常（0）”“中等故障（0.5）”和“严重故障（1）”）。

表1 顶事件及中间事件Tab.1 Top event and intermediate events

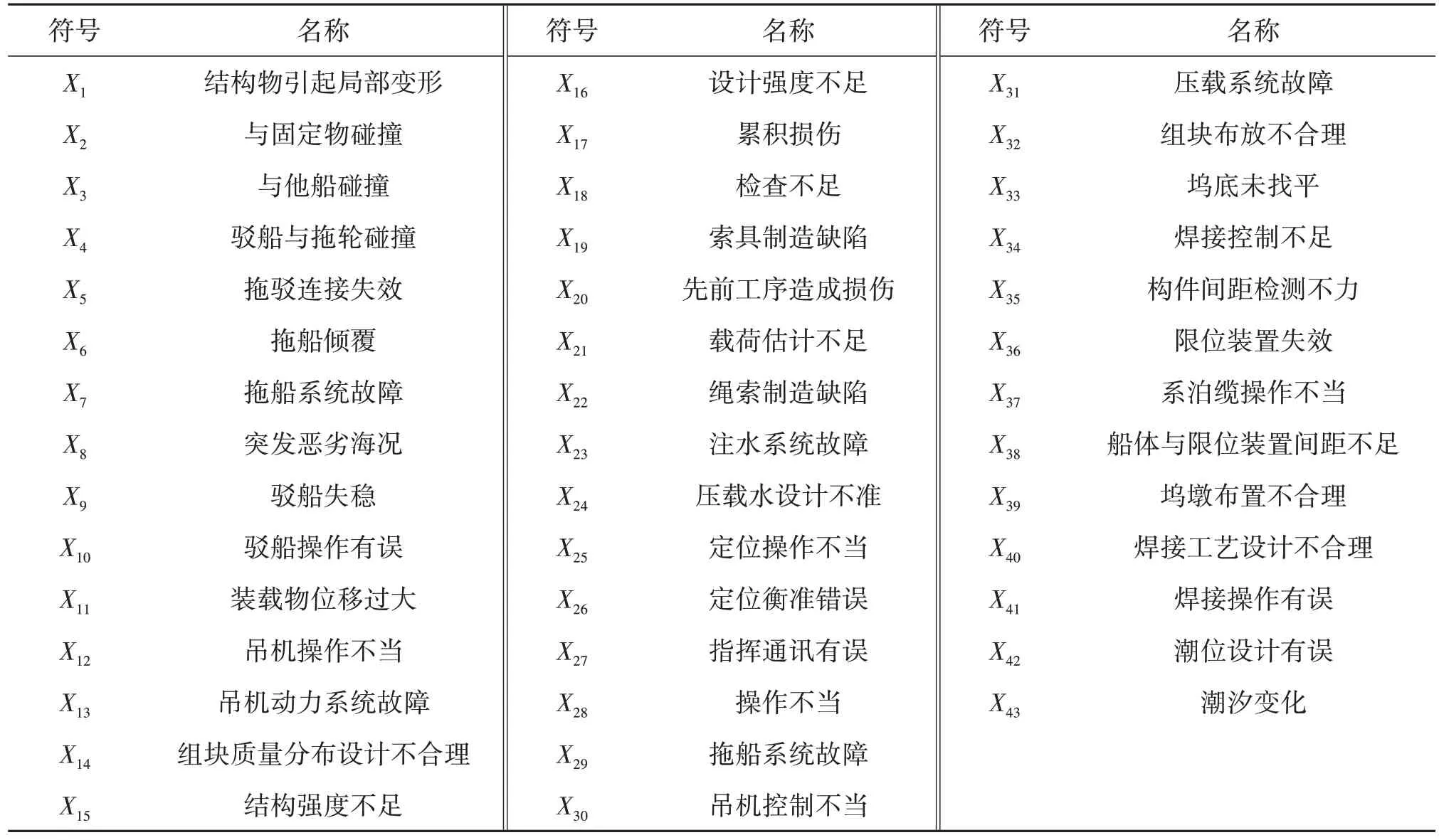
表2 根事件符号及名称Tab.2 Symbol and name of root events

图3 安装作业流程图转换成主贝叶斯网络Fig.3 Installation operation flow diagram converted into the main Bayesian network

图4 深水半潜平台安装作业风险贝叶斯网络Fig.4 Bayesian network for risk of deep water semi-submersible installation

3.2 先验概率和CPT估计

具体实施流程为：①收集整理工程项目历史调查数据资料，为专家评估提供参考；②邀请了5 位专家（E1～E5）结合工程经验及实际项目资料，对照图2给出各根事件状态为1时的评价语义值以及置信度；③采用2.2 节所述方法对5 位专家的评价进行聚合处理，并经模糊化处理转化为各根事件状态为1 时的PFFR，如表3所示。假设根事件状态为0.5和1的PFFR相同；④通过专家评判获取不同事件间的条件概率分布。

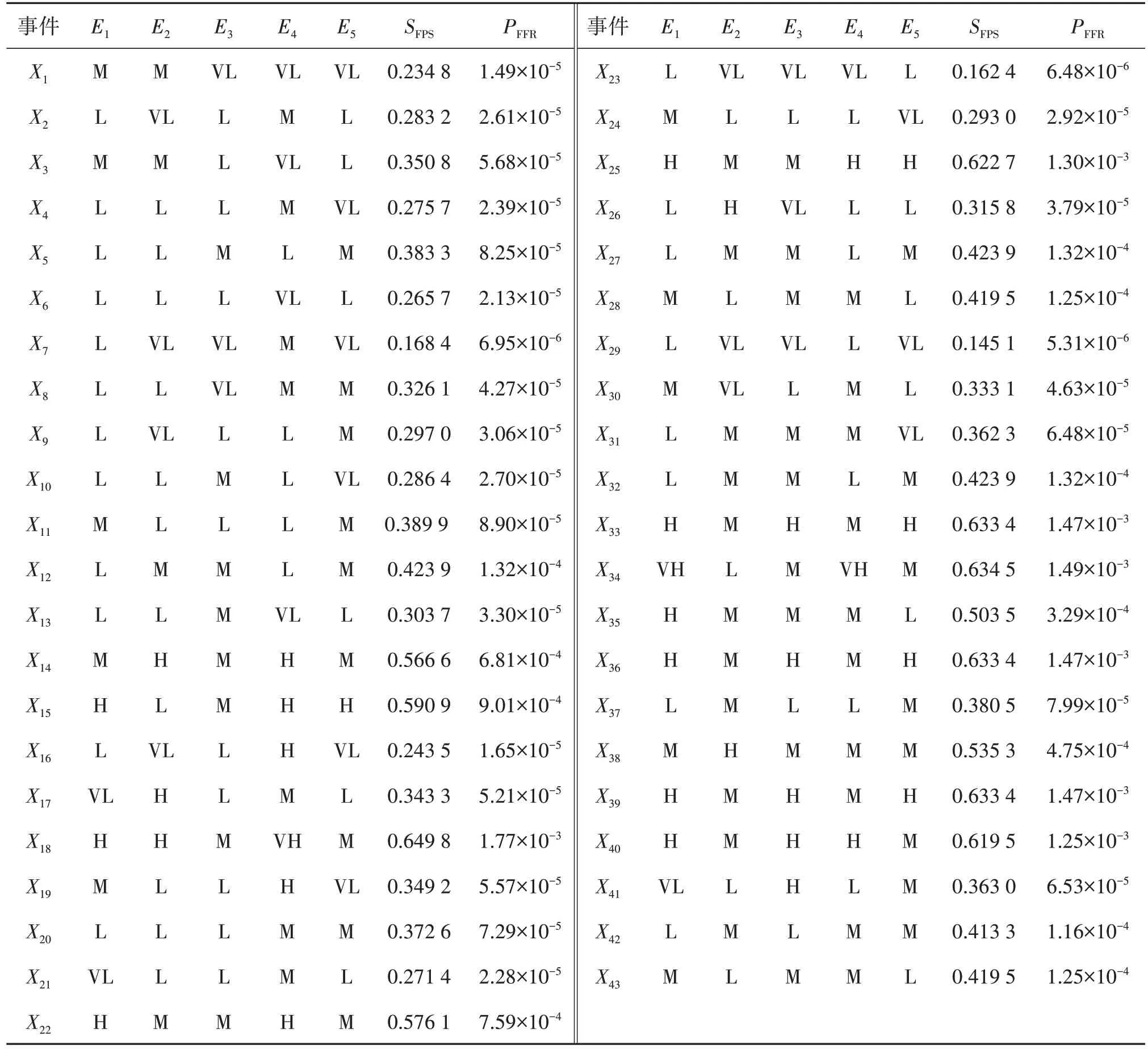
表3 根事件的专家评价、SFPS和PFFR值Tab.3 Expert evaluations, SFPS and PFFR value of root events

3.3 BN推理及结果分析

3.3.1 正向因果推理

在获取了根事件先验概率和条件概率分布的条件下，通过正向因果推理算法，可计算出每个阶段（A1～A5）的失败风险发生概率P（Ai=1）和深水半潜平台安装失败的概率P（T=1）。风险概率如图5 所示。结果表明，随着安装过程的进展，风险概率不断增加。深水半潜平台安装失败的概率很小（P（T=1）=0.073 8）。该平台在安装作业过程中未出现安全超限预警的情况，且实际风险的变化趋势与多态模糊贝叶斯网络模型的计算结果基本一致。在缺乏有效数据的情况下，该模型可以大致确定深水半潜平台安装过程中的风险概率。尽管深水半潜平台安装失败的概率很小，但平台和安装作业的成本都非常高。一旦发生事故，将造成严重损失。为减少和防止风险事件的发生，需要根据实际情况制定安装过程的风险防范计划。

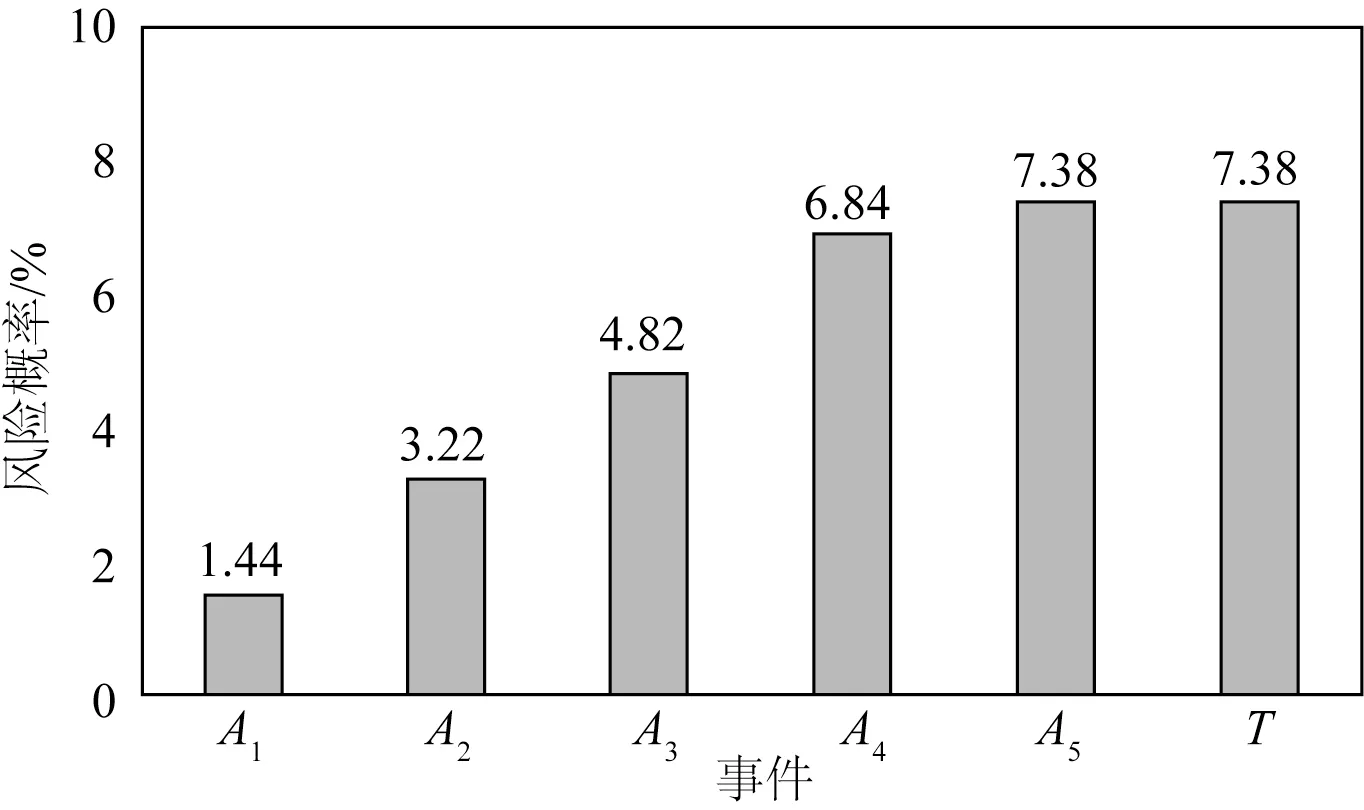
图5 深水半潜平台各安装阶段风险概率Fig.5 Risk probability of deep water semi-submersible platform at each installation stage

随着安装作业过程的开展，现场监测信息不断反馈，新的事件状态可以作为证据输入到BN 中以更新事件概率，实现基于现有信息的实时动态风险预测。例如，当压载系统出现严重故障时，即根事件X31表示的风险事件发生，且状态为“严重故障”时，将P（X31=1）= 1作为实时信息输入到BN 中。计算得到P（T=1|X31=1）=0.261。如果压载系统严重故障已经发生，但未及时维护，此时又出现潮汐变化，风险程度中等，则将P（X31=1）=1和P（X43=0.5）=1都作为实时信息输入到BN中。通过正向推理，计算得到P（T=1|X31=1，X43=0.5）=0.361。此时，安装作业失败发生概率明显增大，管理者需及时采取应对措施，降低风险，保障安装过程的顺利进行。

3.3.2 反向诊断推理

考虑顶事件T= 1发生的情况，实现BN的概率更新，更新后的后验概率如图6所示。如图6所示，坞墩布置不合理（X39），检查不足（X18），定位操作不当（X25），限位装置失效（X36），焊接工艺设计不合理（X40）的后验概率较大，是导致半潜平台安装作业失败发生的可能性较大的风险事件。

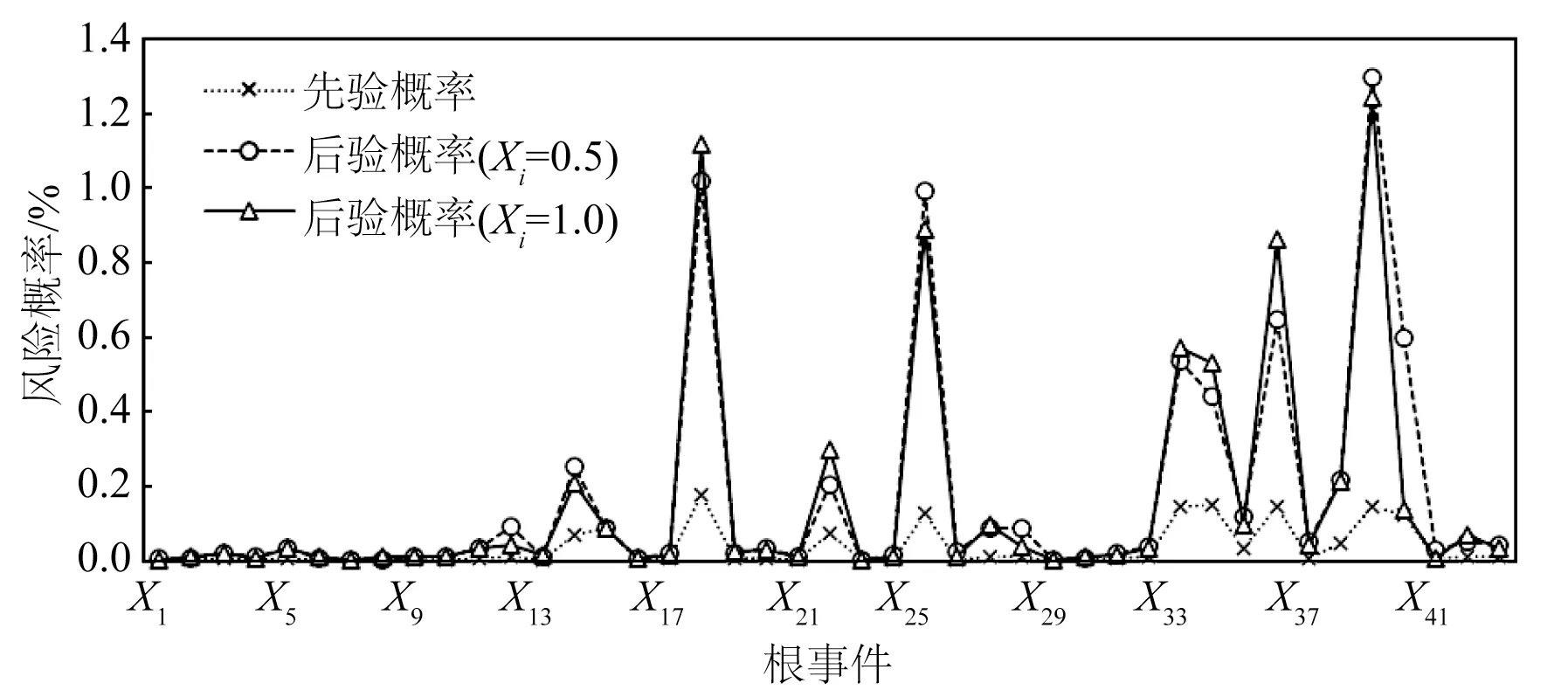
图6 根事件的先验概率和后验概率Fig.6 Prior probability and posterior probability of root event

在顶事件发生的情况下，为了快速判断根事件的可能性程度，可通过诊断推理的方式对BN 中各事件进行概率更新，根据当前条件下后验概率排序，逐一计算每个根事件的后验概率值。如坞墩布置不合理（X39）处于“严重”风险状态时，将P(X39= 1|T= 1) = 1 输入到BN 的反向推理中，计算其他各事件的更新后验概率，如图7所示。据此，可逐一对剩余事件进行快速排查，实现半潜平台安装作业的动态风险分析。

图7 BN动态诊断推理 (P(Xi | T=1, X39=1) = 1)Fig.7 Dynamic diagnostic reasoning of BN (P(Xi | T=1, X39=1) = 1)

3.3.3 敏感性分析

基于构建的BN，利用式（14）计算每个根事件Xi对顶事件T的RoV 重要性程度MRoV。表4列出了10个关键风险因素的MRoV。由表4可以观察到敏感性分析结果与反向诊断推理结果基本吻合。RoV 重要性程度最大的根节点为X39，即坞墩布置不合理。同时可依照以下次序进行重点风险排查：X39、X25、X27、X18、X37。

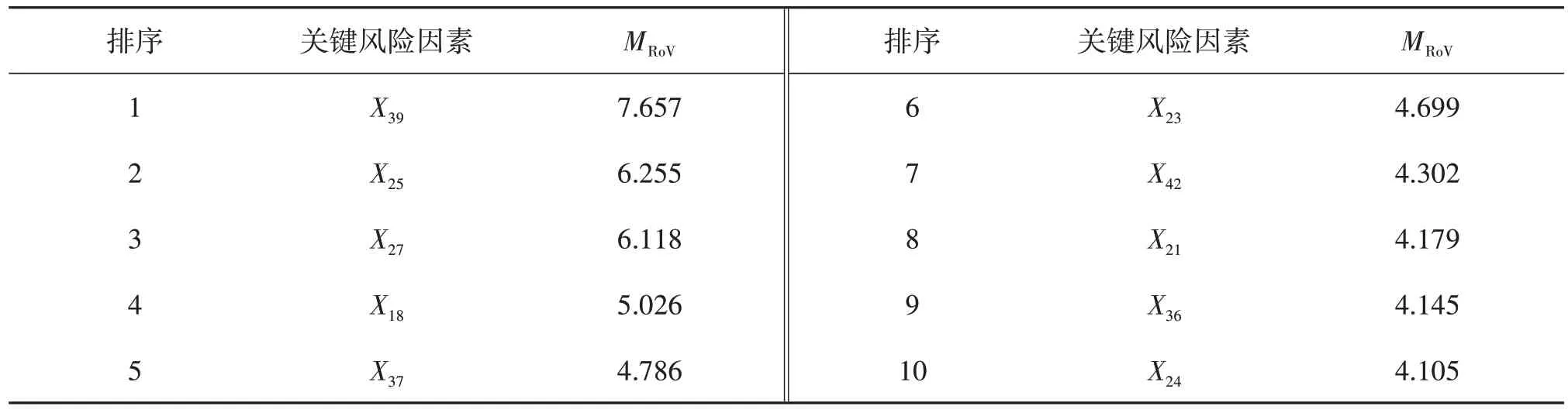
表4 根事件的RoV重要性Tab.4 RoV importance measurement of root events

4 结 语

针对半潜平台安装作业过程的复杂性和语言性评估中存在的模糊性，建立了一种基于PFBN 的风险分析模型，并以陵水17-2项目为例，开展深水半潜式平台安装作业过程风险分析，验证该模型的合理性与有效性，得到以下结论：

1）PFBN 模型能够有效解决多态性和模糊性的问题。与传统方法相比，基于行业规范指南的推荐标准定义模糊数，并采用了一种改进的去模糊化转换方法，保证了专家知识和经验转化为评价数据的合理性。在此基础上，结合置信度指标和相似性聚合法进行专家意见聚合，提高了专家经验和知识的可靠性。

2）基于BN 的双向推理和敏感性分析技术，将风险管理扩展到整个作业过程，而不是局限于事故前的控制，实现了安装作业过程中的实时动态风险分析，降低系统风险并保证过程安全。

3）在海洋工程领域多位专家评价的基础上，对深水半潜式平台安装作业风险进行了PFBN 分析，结果表明坞墩布置不合理（X39），检查不足（X18），定位操作不当（X25），限位装置失效（X36），焊接工艺设计不合理（X40）等事件风险较高，需要重点防控。文中模型不仅可以应用于半潜平台安装作业的风险分析，还可应用于其他复杂工程项目的风险评估工作。