锂离子电池电解液泄漏试验及参数化表征*
刘延超 王宇斌 胡晶 张鹏飞 尹立坤
(1.中国长江三峡集团有限公司科学技术研究院,北京 100038;2.北京交通大学,北京 100044)
主题词:锂离子电池 电解液泄漏 二阶等效电路模型 电化学阻抗谱 弛豫时间分布
1 前言
近年来,我国锂离子电池行业保持高速发展态势[1],但在实际使用过程中,锂离子电池起火、爆炸等事故仍时有发生,安全问题已经成为制约锂离子电池发展的重要因素,因此,对锂离子电池的故障诊断研究日趋重要[2-5]。锂离子电池的故障主要包括漏液故障、过充故障、短路故障和高温故障等[1,6]。目前,关于锂离子电池漏液诊断或检测的相关研究极少,且多基于漏液造成的气体成分变化,缺少基于电池电信号的检测方式,对于漏液后电池性能变化的研究也几乎空白。文献[1]提出了一种基于气体监测的锂离子电池故障报警装置,但电解液泄漏导致的气体成分变化受气流、气压、温度等环境因素影响较大,该方案测量精度差,需在原有电池管理系统上增加气体传感器,提高了使用成本。同时,基于气体的漏液故障检测方法无法判断发生故障的是电池模组中的哪一单体。因此,有必要对电池漏液后的电信号进行采集与研究,寻找与漏液故障相关的特征参数,为漏液故障诊断方法的建立提供依据。
电化学阻抗谱(Electrochemical Impedance Spectros⁃copy,EIS)是确定电池工作边界、评估性能和跟踪功能状态的关键之一[7],广泛应用于电池内部温度估计、析锂检测、荷电状态估计和健康状态估计等。目前,常用的EIS数据解析方法是基于等效电路的拟合技术(如Zview中的fitting 拟合工具),需要对模型进行先验假设,而文献[8]提出的弛豫时间分布(Distribution of Relaxation Times,DRT)法能直接确定时间常数的数量和大致频率范围,可极大地减少试验工作量和分析上的不确定性[8-9]。文献[10]和文献[11]将DRT方法成功应用于EIS分析领域,解决了以往电化学阻抗谱分辨率低、不易解析等问题,为本文的研究提供了可靠理论依据和方法。
少量的电解液泄漏并不会立刻导致电池的交、直流阻抗发生明显变化,因此需要对电池进行长期循环试验,这也有利于探究电池的循环过程是否会加剧漏液故障。本文将基于正常电池和漏液电池的循环老化试验、直流阻抗测试和EIS测试,从二阶等效电路模型参数变化、电化学阻抗谱DRT环节变化,研究锂离子电池电解液泄漏的表征参数,为漏液故障诊断提供参考。
2 试验方案
2.1 漏液故障模拟及循环试验
本文采用7 只18650 型三元(NCM523)锂离子电池,该型电池标称容量为2.6 A·h,充电截止电压为4.2 V,放电截止电压为2.75 V。所有测试均在25 ℃高低温箱中进行。流程如下:
a.使用直径为0.6 mm 的电钻,分别在4 只电池(依次记为L1、L2、L3、L4)正极的极壳顶部钻孔,模拟漏液状态电池;另外3 只电池(记为N5、N6、N7)作为正常对照电池。
b.同时对7 只电池进行直流阻抗测试及EIS 测试。
c.对L1、L2和N5、N6进行连续的循环老化测试,对L3、L4 和N7 进行间断的循环老化测试,直到有电池出现老化现象,即电池容量衰减为初始容量的80%,停止测试。
其中,连续的循环老化测试是连续对电池进行循环充放电,以50 次循环为1 个周期。充电方式依照电池手册提供的方案,采用恒流恒压(Constant Current Constant Voltage,CCCV)模式,先以0.5 C 恒流充电,达到4.2 V 后,切换为恒压充电,直到电流倍率下降至0.05 C。充电结束后静置15 min,以2 C的电流倍率,恒流放电至2.75 V。间断的循环老化测试是以12次充放电循环为1个周期,先进行10次循环,在第11次循环充电结束后搁置120 h,放电至2.75 V,继续进行第12次循环。2 种测试,在每个循环周期开始前都要更新容量,按照既定的电流倍率修改充放电电流。
d.循环老化测试结束,对所有电池进行直流阻抗测试及EIS测试。
循环测试结束时,L1、L2 和N5、N6 进行了150 次左右的充放电循环,L3、L4 和N7 进行了50 次左右的充放电循环。
2.2 直流阻抗与交流阻抗测试
直流阻抗测试基于等效电路模型对电池直流脉冲响应进行拟合,获取反映电池直流阻抗的模型参数。交流阻抗测试通过施加正弦纹波电流或正弦纹波电压,根据激励信号与响应信号之间的频率、幅值、相位关系,得到电池在一定频率范围内的EIS[7],一般在复平面上表示,即奈奎斯特(Nyquist)图,其横、纵坐标分别为交流阻抗的实部和虚部[12-14]。
测试前的静置时长和锂离子电池所处的荷电状态(State Of Charge,SOC)都会影响测试结果。本文分别在SOC 为10%、20%、30%、60%、90%时静置1 h,施加0.5 C(1.3 A)、持续1 min 的正脉冲电流进行直流阻抗测试,脉冲测试采样时间为0.01 s。待直流阻抗测试结束,再静置1 h 后进行EIS 测试,所选电流为正弦纹波电流,控制电压波动幅值不超过10 mV,频率范围10 kHz~0.01 Hz,每10倍频程取10个频率点。
测试平台包含用于电池充放电的多通道电池测试系统Arbin-LBT、用于控制恒温25 ℃的温箱SPX-150BIII、用于EIS 测试的电化学工作站Bio-logic VMP-300、温度采集仪HIOKI-LR8510及无线温度记录仪HIOKI-LR8410-30。
图1 所示为循环老化测试后,30%SOC 处各电池的EIS,其中Zre、Zim分别为阻抗实部和虚部。漏液电池的阻抗实、虚部均明显大于正常电池,但曲线形状相近,说明在漏液前、后,锂电池阻抗的构成环节基本一致。
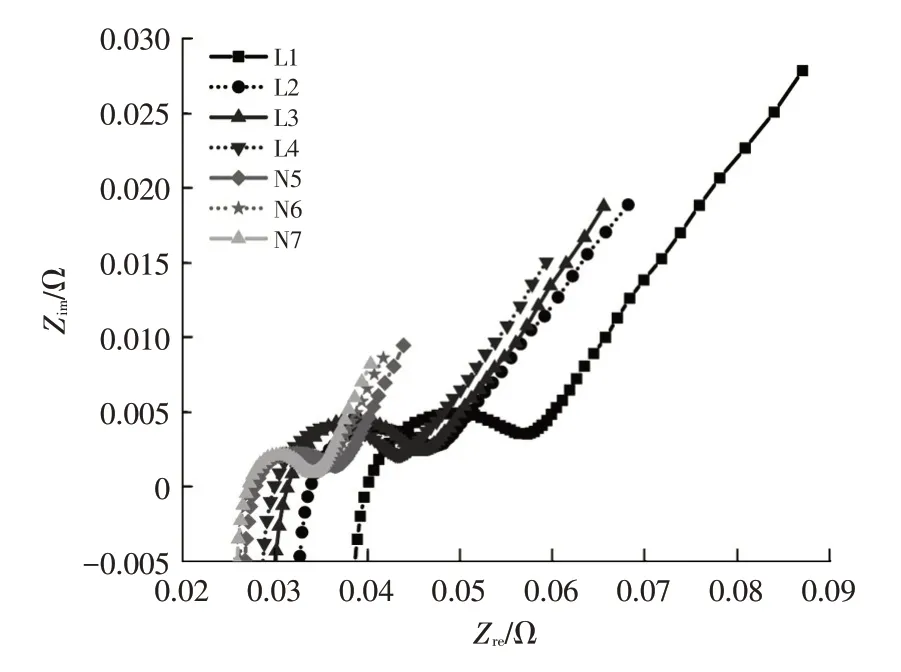
图1 30%SOC处各电池的EIS
3 直流阻抗分析方法与结果
3.1 二阶等效电路模型
锂离子电池的二阶等效电路模型表达式简单,综合性能好,能够较全面地描述系统状态,由2个RC网络结构和1个电阻串联而成,如图2所示。
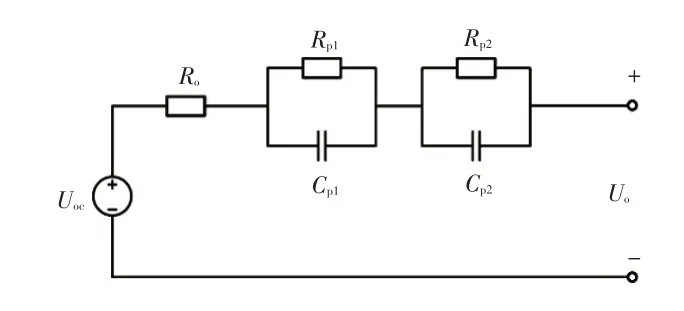
图2 二阶等效电路模型
该模型的数学表达式为:
式中,Uoc为电池的开路电压;Ro为电池欧姆内阻;U1为Rp1及Cp1两端的电压;U2为Rp2及Cp2两端的电压;Rp1、Rp2为电池的极化内阻;Cp1、Cp2为电池的极化电容;I为负载电流;Uo为模型端电压;t为时间。
由式(1)可得模型端电压Uo(t)的计算公式为:
其中,Ro为直流阻抗测试脉冲开始后第0.01 s的欧姆内阻,计算公式为:
基于电路的非线性特性,将Rp1、Rp2、Cp1、Cp2的辨识问题转化为非线性最优化问题。由式(2)可知,对于任意θId=(Rp1,Rp2,Cp1,Cp2),任意t时刻都有唯一确定的Uo(t)与之对应:
求解该非线性最小二乘优化模型的全局最优解θId,即完成二阶等效电路模型的参数辨识。
3.2 直流阻抗表征参数
以最小二乘法辨识所有电池在不同SOC下,前10 s充电脉冲的模型参数。其中,L3在0%SOC处的θId残差平方和最大,为5.662×10-5。图3展示了L3在0%SOC下的拟合结果,其中Vp为模型中2个RC环节的电压之和,拟合结果与实测结果基本重合。通过参数辨识,获得二阶等效电路模型的参数集:θModel=(Uoc,Ro,Rp1,Rp2,Cp1,Cp2,τ1,τ2),其中τ1、τ2为2个RC环节的时间常数。
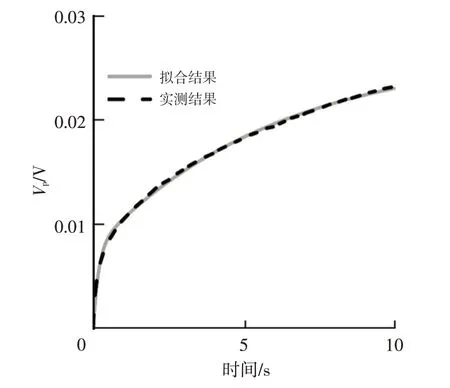
图3 L3在0%SOC下的拟合结果
图4 展示了循环老化后,部分电池参数的辨识结果。漏液电池的Ro、Rp1、Rp2普遍大于正常电池,而Cp1、Cp2小于正常电池,说明电解液泄漏会导致锂离子电池的欧姆内阻和极化内阻增大,极化电容减小。图4a、图4b、图4e 中,对于Rp1、Rp2、Ro,除部分SOC 点外,L2 高于L3,N6略高于N7,说明随着循环次数增多,漏液故障导致的内阻增大现象会加剧。图4c和图4d中,对于Cp1、Cp2,L2低于L3,N6低于N7,但L2和L3之间的差距明显较N6和N7间的差距小,说明循环次数越多,锂离子电池的极化电容越小,但漏液故障削弱了极化电容的减小趋势。
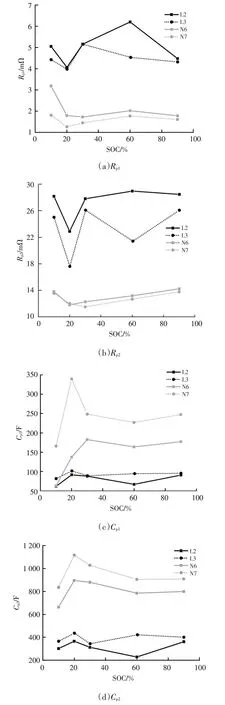
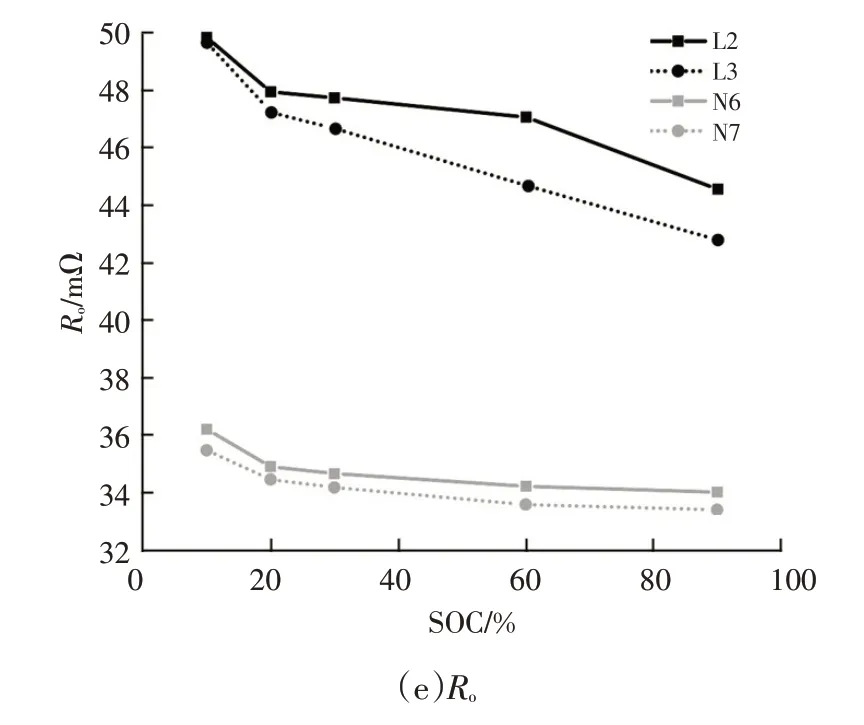
图4 二阶等效电路模型辨识结果
漏液电池和正常电池在Ro、Rp1、Rp2和Cp2的全SOC区间内,可以良好区分,曲线无相交部分;而Cp1曲线在10%SOC 处相交,难以区分。因此,上述5 个参数均可以表征漏液故障,但只有Ro、Rp1、Rp2和Cp2可作为全SOC区间内的漏液故障表征参数。
4 交流阻抗分析方法与结果
4.1 DRT分析基本原理
弛豫时间是系统的某一变量由暂态趋于稳态所需要的时间,在电化学系统中,弛豫时间和特征时间常数相对应,弛豫时间分布和特征时间常数分布相对应[8]。对于锂离子电池,通过DRT方法可以在不预先建模的情况下,提取电池内部化学反应过程中时间常数的分布,也能够有效分离EIS图中相互重叠的化学反应环节。
电池交流阻抗可表示为:
式中,f为电流或电压激励的频率;τ、g(τ)分别为弛豫时间常数及其分布函数;i为虚数单位。
目前,计算g(τ)的方法有正则化方法、运算微积分、最大熵、遗传规划、傅里叶变换、蒙特卡洛抽样法等[8]。本文所采用正则化方法[12],运算较简单,抗噪性可调。由于频率常在对数尺度上采集,因此式(6)亦可写作:
式中,γ(τ)=τg(τ)为在时间常数域内连续的函数。
对γ(τ)求解,首先要将其近似为数量为M的函数之和:
其中,ϕμ=exp(-(μx)2)为γ(τ)的基元函数;μ可视作函数ϕμ的形状因子,与ϕμ的半峰全宽[11]有关;xm、τm分别为第m个基元函数的权重和时间常数。
将式(8)代入式(7),可得:
最后,用式(9)拟合测得的EIS 数据,计算出x=(x1,x2,…,xm)进而得到γ(τ)与τ的对应关系。
4.2 交流阻抗特征参数
图5 所示为对所测30% SOC 处EIS 进行DRT 运算的结果,弛豫时间常数τ与频率f相关,τ=lg(f)。所有电池经DRT 运算,均可以得到4 个峰,对应于电池内部4个化学反应环节,将其峰高(Peak)按照频率从低到高(τ从大到小)依次命名为P1、P2、P3、P4。7 只电池在初始状态下的EIS曲线基本重合,故对其进行DRT分析后取平均值,作为电池初始状态的DRT曲线。
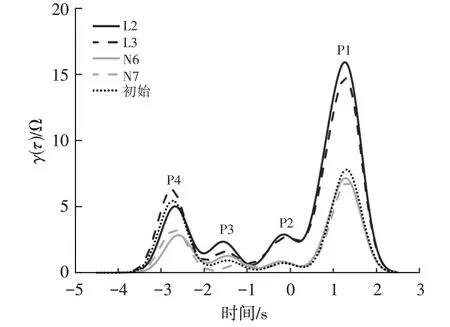
图5 电池在30%SOC处DRT曲线
直观上看,漏液电池的4 个峰普遍高于正常电池,连续循环老化电池和间断循环老化电池的峰值和各峰所对应的τ也不相同。为了得到更加具体的结论,将各峰所对应的峰高、峰面积和弛豫时间常数τ作为DRT 进行提取。经对比,峰面积和峰高的数值虽然不同,但变化趋势一致,对于DRT 表征效果相同,τ相对于前两者而言,变化率极低,因此选择峰高作为主要分析对象。
图6所示为循环老化试验后,P1、P2、P3、P4相对于初始状态的变化率。与正常电池相比较,漏液电池的变化率普遍更大。其中:漏液电池的P2变化最为明显,最大变化率达298.1%;P3的变化率次之,最大可达200%;P1 的最大变化率为118.4%;P4 的变化率最小,且仅有L3 电池的P4 为正值,其余电池变化率均为负。正常电池的P1、P2 变化率均远低于漏液电池,而P3 的变化率曲线与漏液电池有交点。因此,选择P1、P2作为区分电池是否漏液的关键特征。
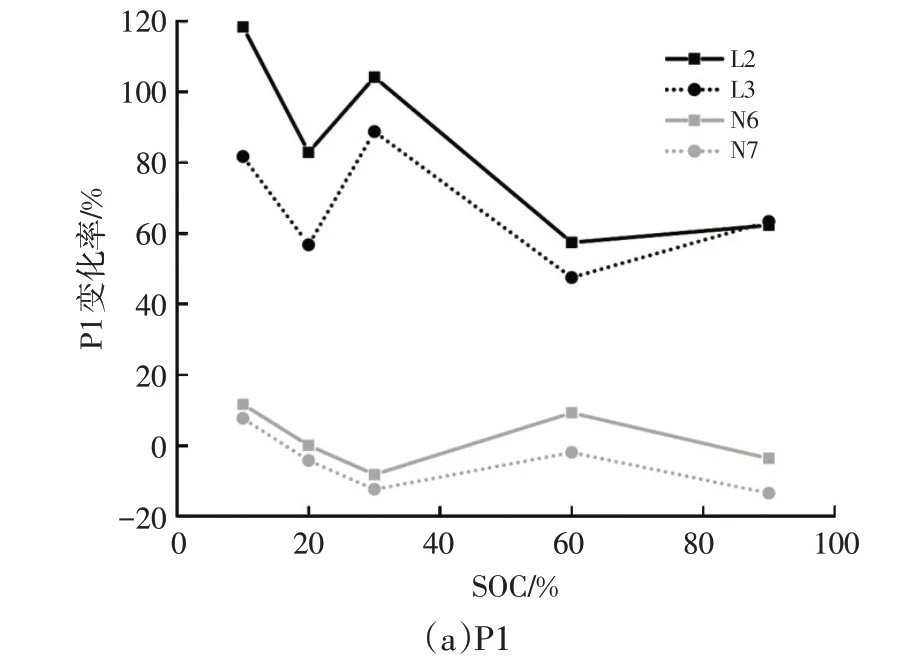
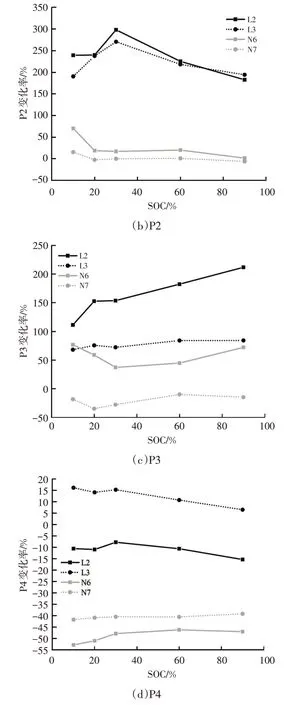
图6 DRT峰高变化率
此外,由图6c可知,连续循环电池的变化率较正常电池高,说明循环次数的增加会使P3增大。由图6d可知,连续循环电池的变化率低于正常电池,说明循环次数的增加会导致P4 减小。图6a~图6c 中,L2 的峰高变化率普遍较L3 高,说明循环过程也会加剧漏液故障对电池造成的影响。
5 结束语
本文对漏液和正常状态锂离子电池均进行了连续循环老化和间断循环老化试验。根据锂离子电池在循环老化后的直流阻抗测试结果,对二阶等效电路模型的参数Ro、Rp1、Cp1、τ1、Rp2、Cp2、τ2进行了辨识,找到了在全SOC 区间内均可表征漏液故障的参数,即Ro、Rp1、Rp2和Cp2。通过DRT方法分析了各电池在不同SOC下的EIS,得到对漏液故障表征明显的DRT 环节为P1、P2。同时还发现循环次数和电解液泄漏对一些环节有明显不同的影响,如P3、P4。研究从锂离子电池直流阻抗、交流阻抗2个角度对锂离子电池的漏液特征进行了分析,为锂离子电池的漏液故障诊断提供新的思路。

