丰富具身经验 培养量感素养

摘要:小学数学知识结构在形式上是由节点和连线组成的复杂网络,教学中,教师应重视知识的前因后果、发生和发展过程,对这一类课进行关联思考和整体设计,帮助学生整体建构知识体系,这对于学生有意义地掌握知识、形成技能、培育素养有着重要价值。
关键词:结构;具身经验;量感;素养
“角的度量”这部分内容属于《义务教育数学课程标准(2022年版)》(以下通称“新课标”)“空间与图形”领域中“测量”的内容。在学习此内容之前,从纵向来看,学生已经学习了“角的初步认识”,知道了角有大小,“角的大小与两条边张开的大小有关,与角的两条边长短无关”;从横向来看,学生已经学习了线段的度量,经历了建立长度单位表象、统一长度单位的过程。“角的度量”和线段的度量、面的度量虽然分布在不同的年级,但它们是具有内在联系的知识。角的度量本质就是用度量单位的个数描述角的大小,其关键在于找度量单位。这就需要教师让学生直观感知角有大小及角的可测量属性,进而进行角的比较,并在描述角的大小过程中产生统一单位的需求,所以本节课应抓住“度量单位”这一核心概念统领教学。
一、寻找度量标准的统一过程,形成具身经验
统一性是计量的本质属性。测量长度需要一把“长度尺”,因为“长度尺”上有统一的长度单位。“角的度量”教学着力点不在于引出量角器,而是帮助学生引出角有大小,大小是由标准的个数所决定的。然而,角的大小非常抽象,因此,用学生熟悉的钟面作为载体,可唤醒学生已有的认知基础,变抽象为直观。动态的分针能让学生直观感悟角的动态生长,而钟面上的大格、小格就成了比较角的大小的参照物,这样的学习素材有利于学生自主生成多种方法去比较角的大小,自然生成“标准”意识。
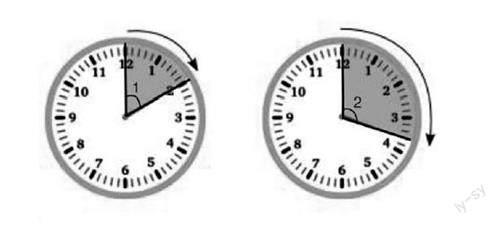
师:观察主题图(见上页图1),小东和小丽上学路上所用的时间为分针扫过的两个角,你能比较它们的大小吗?
【比一比】
你能想到几种不同的方法来比较下面∠1和∠2的大小?
【说一说】
和组内小伙伴们分享自己的思考过程。
第一小组用数格子的方法进行比较。
生:我用“数大格”的方法,∠1是2个大格,∠2是3个大格还多,所以∠2大。
生:我用“数小格”的方法,∠1是10个小格,∠2是18个小格,所以∠2大。
师:用“大格”或者“小格”作为标准,谁含有的标准数多,谁就大。角的大小由标准的个数决定。
第二小组用三角板上的角作为标准进行比较。
生:我是用直角作为标准来量的,∠1比直角小,∠2比直角大,所以∠2大。
生:我是用三角尺上的大锐角为标准来量的,∠1等于大锐角,∠2比大锐角大,所以∠2大。
生:我是用三角尺上的小锐角为标准来量的,∠1等于2个小锐角,∠2比3个小锐角大,所以∠2大。
师:用三角尺的角作为标准,分别测量两个角的大小,再作出比较。
第三小组用直尺量出角张开的距离进行比较。
生:角的大小跟它两条边张开的大小有关,我们小组量出∠1张口的大小是3厘米,∠2张口的大小是5厘米,所以∠2大。
师:比较∠1和∠2的大小,通过刚才三个小组的交流汇报,你有什么发现?
生:比较角的大小,首先要确定一个标准。
生:我想补充一点,标准越小,结果越精确。比如小格比大格度量的结果精确,小角比大角度量的结果精确。
生:角的大小与两条边张开的大小有关,里面含有的格数越多,角越大。
生:大格对应的圆弧长,小格对应的圆弧短。
师(小结):角的大小与两条边张开的大小有关。在同圆中,大角对应的弧线长,小角对应的弧线短。我们要测量角的大小,在测量之前要用统一的单位进行度量。
教师引领学生经历了理解角的内涵的不同层次:直观感知角有大小,角在钟面上开口变大,就是角变大了;寻找标准,用“小角”度量大角,用“数+单位”来描述角的大小。学生在寻找度量标准的统一过程中,不断累积具身经验,唤醒度量意识。
二、经历单位量感的建构过程,发展度量意识
数学结构化教学注重把概念的形成镶嵌于知识体系之中,以核心概念为中心,用思想方法建构起知识网络,通过横向联系知识实现旧知迁移,促进新知的学习。如度量长度,应使用一个规定的长度作为长度单位,要知道一条线段的长度,就要看被测量的长度里含有几个这样的长度单位。对于二维空间里的角,教师要让学生感受到“描述一个角的大小,就是看大角里面含有几个小角”。因此,教师要引导学生借助钟面上的大格、小格所对应的角作为标准,来测量角的大小。
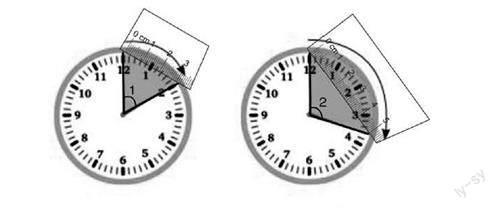
【量一量】
选择合适的标准角分别量出下面两个角的大小。
∠3=()个()角 ∠4=()个()角
师:刚才同学们借助不同的“标准”进行比较,都得出∠2大于∠1,一起回顾一下,我们怎样测量物体的长度?
生:我們创造长度单位1厘米、1分米、1米,用长度单位去测量。
师:大家从中受到什么启发?
生:量大长度用小长度作为标准,量大角要用小角作为标准。我们可以用钟面上一大一小这两个角作为测量工具。
师:我们把钟面上一大格对应的角称为大格角,一小格对应的角称为小格角,借助学具袋中的大格角和小格角,分别量出∠3和∠4各有多大。
师:先来汇报你们是怎么测量∠3的,具体结果是多少。
第一小组:我们小组测量到∠3等于2个大格角多一点儿、3个大格角少一点儿。
第二小组:我们同时用大格角和小格角,∠3等于2个大格角和2个小格角。
第三小组:我们全部用小格角,∠3等于12个小格角。
师:大家在测量的过程中,用大格角和小格角结合起来测量,非常好,合适的是最好的。那∠4有多大?
第一小组:我们小组用大格角和小格角都測了,都不正好。
第二小组:我们小组测到1个大格角加半个小格角,或者全部用小格角测,是5个半小格角。
师:大家有没有听清楚?怎么出现了半个?
生:1个小格角还大,我们把它对折,就正好,所以最后有半个。
师:这个小组太厉害了,1个还大,继续细分,得到更小的单位。大家联系我们学过的长度单位,是否有所启发?
生:我们可以找到一个很小的角,把它看作“1”,用这个“1”去度量角的大小,数一数就知道了。
师:你真有想法。让我们一起看一下角的度量单位是怎样产生的。
教师引入介绍:将半径旋转一周形成的角叫周角,规定为360度,把它平均分成360份,其中的1份就是1度的角。度是角的计量单位,用符号“°”表示,如1度记作1°。
∠3(72°)不能用大格去度量,只有用大格结合小格才能度量。∠4(33°)用大格结合小格仍无法表达出角的大小,学生从而产生继续细分的想法。学生在这样一步步的思维行进过程中认识到,角也像长度一样,要想知道一个角的大小,就要用统一的度量单位来测量;要准确测量角的大小,就要确定合适的度量单位。对于同一个大角,单位小角的不同,导致了对角的大小的描述不同,所以,单位小角还需要进一步完善,寻找一个单位小角的标准(1°角)。学生在新旧知识的类比推理中实现正向迁移,自然生长出对1°角的需求,为知识关联找到了认知通道。学生经历单位量感的建构过程,完善了认知结构,发展了度量意识。
三、加强累加量感的感悟过程,精准完善量感
量感在日常教学中往往被教师视作“规定”知识,直接告诉学生,从而掩盖了知识产生的过程,忽略了背后鲜活的体验。在核心概念统领下的结构化教学中,教师应着力于激发学生在认知冲突中思考,引导学生经历标准量的建构、量角器的形成过程,把抽象的量感与具体的体验相结合,在积累丰富活动经验的基础上,将量感内化为稳定的表象。
师:思考一下,测量长度,可以把长度单位累加形成长度尺,便于用来测量。是否可以借助这样的经验,创造出适合我们使用的量角工具?
【创一创】
在透明的半圆形胶片上创造出一个量角的工具,标出数据。教师课件演示:0刻度线出发,动态产生1°角,1°角通过累加得到5°,10°,30°,60°,90°,180°角。学生借助课件演示,体会每个角都是由若干个1°角拼合而成的。
师:观察量角器,你有什么发现?
生:量角器是由1°角不断累加而成的,与长度尺不同的是,长度尺是从0刻度线依次往右不断增长的,而量角器的刻度线是旋转而成的,角的顶点一直不变,中心就是角的顶点。
师(小结):确定了角的计量单位,有了1°角,读懂了量角器的构成,我们就可以准确地测量角的大小了。
师:动手量一量∠3和∠4的大小,说一说,你是怎么测量的。
生:角的顶点与量角器的中心对齐,一条边与0刻度线对齐,另一条边对着几,就是几度。∠3=72°,∠4=33°。
师:请利用我们创造的量角器来测量一下∠5的度数。
生:我测得∠5=120°。
生:∠5不可能大于90°,因为它比直角小。∠5的一条边对齐180°刻度线,不是对齐0°刻度线,所以应该用180°-120°=60°。
生:我把量角器旋转了一下,一条边对齐0刻度线,我也测量到是60°。
师:观察∠5,它与∠3、∠4。有什么不同?
生:开口的方向不同,所以测量起来容易出错。
师:人们在测量角的大小过程中,也发现了这个问题,怎样才能解决开口反向的问题?
生:我们在外面再标一组数据,左边180度刻度线对应0刻度线,这样就可以“一尺两用”了。
师:你和双向量角器的发明者想得一样。请大家拿出量角器,观察各部分组成。刚才,我们创造了量角器,积累了测量经验,接下来,请用我们学到的知识去估计一下生活中角的大小(见图2)。
生:图2中的左图可以分成一个直角和一个锐角,锐角大约是90°的一半,所以大约是135°。
生:图2中的右图,左边的锐角估测比直角少一个锐角,锐角大约是30°的一半,所以估计75°。右边那个角用180°减去75°,大约是105°。
师:借助30°,45°,60°,90°等这些特殊的角进行估计,是估测的一个有效策略。下面请用量角器验证一下估测的结果。
角的度量的本质是看被测对象中含有多少个“单位小角”,这是学生理解量角器的逻辑基础。量角器的本质是“单位小角”的不断累加,用1°累加成2°,3°,10°,30°……学生在这个过程中,首先感受到角的有限可加,进而认识更多的度数,明白“度量的对象里包含了多少个度量单位就是多少度”。其次,所有这些角的顶点都重合在一个点上,而这个点就是量角器的中心点,同时也是角的顶点,这也为角的顶点与中心点重合找到了思维的根基。最后,在实际测量中,学生感受到了单边一圈量角器的不足,自然产生了完善量角器的需求,在外圈再反向(顺时针)标一圈刻度,让内圈刻度与外圈刻度完美对应,突破了量角器上两圈刻度读法的难点。教师再引导学生在量角器上找角、估角与量角、生活中找角,帮助学生加强对量的深度体验、对单位量的感知以及对累加量的感悟,形成了不同单位量的表象,拓展了度量单位,丰富了量感。
量感的培养是一个较长期的、反复体验、不断矫正的过程,与学生个体的活动经验有关。学生能根据实际情况灵活地选择不同的度量单位进行度量,这是量感发展的最高境界。
参考文献:
[1]梁培斌,张先锋. 量感的内涵、特征、价值与培养策略[J]. 江苏教育,2020(65).
[2]韩宇玫.在小学数学中开展量感可视化教学的策略[J].辽宁教育,2021(19).
(责任编辑:杨强)
作者简介:陈金飞,江苏省启东实验小学特级教师,正高级教师。

