污染场地多相抽提低碳修复布井方案优化模拟研究

金嘉路，杨逸文，王 震，张婉莹，周 龑，张 峰，李 磊，崔长征

1. 华东理工大学资源与环境工程学院，国家环境保护化工过程环境风险评价与控制重点实验室，上海市环境保护化学污染物环境标准与风险管理重点实验室，上海 200237

2. 上海市环境科学研究院，国家环境保护城市土壤污染控制与修复工程技术中心，上海 200233

3. 中石化第五建设有限公司，广东 广州 510145

4. 上海格林曼环境技术有限公司，上海 200001

5. 中石化炼化工程（集团）股份有限公司洛阳技术研发中心，河南 洛阳 471003

多相抽提(multi-phase extraction，MPE)是一种通过“抽提井”真空提取污染区域地下的气体、地下水和非水相液体(non-aqueous phase liquids，NAPL)，将污染物分离和处理的原位场地修复技术，作为气相抽提(soil vapor extraction，SVE)的改进技术已被广泛应用于实践，可以与空气注入与原位热脱附等其他技术联合应用强化修复效果[1-3]. MPE 修复对于中高渗透性的土壤具有较好的修复效果，在我国，张峰[4]在华东地区某工厂甲苯污染砂质粉土场地进行了MPE修复中试试验，在25 d 内总共去除甲苯污染物约125 kg，占总去除NAPL 污染物的85%，部分监测点修复后未检出NAPL 残余. 张晶等[5]在某有机复合污染砂质粉土场地应用MPE 和原位化学氧化技术进行了联合修复，45 d 的修复周期内收集了约100 L 的LNAPL，污染物去除率大于90%.

修复井间距对场地修复具有重要意义，NAPL 污染场地修复常存在拖尾与反弹现象[6]，Bass 等[7]对44 个实际场地的修复案例的调查结果显示，当单井所需修复的半径小于5 m 时，往往能无反弹修复，而所需覆盖半径超过7 m 时，修复往往失败. 现有的研究显示，土壤渗透率等水文地质因素对抽提井影响半径和修复效率有着极大的影响[8-10]，然而，目前MPE现场实践通常依据工程经验均匀布设抽提井，没有针对场地渗透率等水文地质条件及污染羽分布设计布井方案，常采用密集的梅花桩布点法布设抽提井，导致MPE 修复效率低、成本高. 因此，如何根据场地情况优化MPE 布井方案和工艺，降低修复成本，提升抽提效率，降低碳排放量备受关注[11-12].

由于实际场地的复杂性和不确定性，单独探寻各渗透率等地质参数下的抽提井影响半径没有实际意义[11,13]，近年来，越来越多的研究者通过TMVOC、GMS、MT3DMS 等商业软件及模型，利用数值模拟研究土壤地下水修复过程，优化布井方案和操作工艺[14-17]. 这一过程中，部分研究者通过模拟软件刻画实际污染场地模型，经人工调参的方式，修改模拟参数，比选最佳修复工艺和布井方案[18-19]. 但人工调参试错法机械重复性强，往往只能涉及50~100 次的工作量，为减少人工试参的过程，也有研究者基于模拟软件的模拟结果，建立简化替代模型，利用MATLAB等数据处理软件结合优化算法计算最优方案[20]，但替代模型的精确度会影响优化结果的正确性. 为此，部分研究者直接利用外部程序调用地下水模拟软件，结合优化算法计算最优布井方案和操作工艺，其中基于MT3DMS 开发的模块化地下水优化软件(modular groundwater optimizer，MGO)被广泛应用在地下水抽出问题中[21]，该方法在保证模拟准确性的同时也免除了人工调参过程. 耿国婷等[22]利用MGO 模拟三氯乙烯污染含水层的抽水修复过程，利用遗传算法优化抽提井布井位置及抽水量等工艺参数，减少了18%的运行成本，提升了经济效益. 但MGO 基于的模拟软件MT3DMS 主要适用于地下水抽出修复，其修复区域主要为地下水含水层，而MPE 过程涉及气、液、NAPL三相变化，修复区域包含包气带和含水层，现有研究普遍采用针对多相运移问题开发的TMVOC 软件模拟MPE 修复过程[9,23-24].

TMVOC 是由美国伯克利实验室开发的基于质能守恒、亨利定律等物理化学理论规律模拟多相流体在饱和-非饱和带运移的模拟软件，能够有效模拟抽提修复过程，反应修复过程中污染物浓度等参数变化. 孙超等[25]和王颖[9]分别通过TMVOC 模拟了场地中热强化SVE 修复过程和苯系物在一维土柱的垂向迁移过程，TMVOC 模拟结果与试验数据的拟合优度(R)分别为0.995 和0.89. 在对场地模拟还原的基础上，研究者基于TMVOC 模型探究了抽提修复过程中的主要影响因素与最优参数，王颖[9]通过TMVOC模拟对15 个场地的SVE 修复效果的影响因素进行了灰色关联度分析，结果表明土壤渗透率的关联度最高，为0.841. 田蕾等[23]通过TMVOC 对苯和乙烯污染的低渗透场地模型的MPE 修复过程进行了模拟，探究抽提井开筛位置的最优设计参数，结果显示，抽提井开筛最优位置应处于含水层深部. 近年来，已有研究者开始尝试将TMVOC 与优化算法相结合，如Sookhak 等[11]利用TMVOC-MP 与遗传算法相结合，优化了MPE 修复场地中抽提井水平布井方案，指出均匀布井方案并非最佳修复方案. 现有的优化研究尚缺乏对污染场地内每口抽提井开筛位置的优化探讨，实际修复过程中，抽提井开筛位置位于非饱和区时修复以气相污染物抽取为主，而位于饱和区时修复以地下水和自由相NAPL 抽取为主，统一的抽提井的开筛位置难以达到最优抽提效果[26]，针对开筛位置的优化修复方案具有必要性.

因此，本研究利用MATLAB 实现遗传算法和TMVOC 软件调用，构建了基于场地污染羽分布和土壤渗透率、有机碳含量等水文地质条件优化MPE 修复方案的MATLAB-TMVOC 联合优化程序，在优化布井水平位置的同时优化各抽提井的开筛位置，并探究了不同数量井群的最优布设及开筛位置，总结了不同土壤渗透率下的最优布井规律，以期为实际现场抽提井布设提供指导，实现高效和低碳修复.

1 研究方法

1.1 MPE 模拟与优化软件

本研究所涉及的软件包括数据处理软件MATLAB(R2021a，MathWorks，Inc.，美国)、地下水模拟软件TMVOC(TOUGH2-TMVOC， Lawrence Berkeley National Laboratory，美国)和地下水模拟及可视化软件PetraSim(Version 5.1，RockWare，Inc.，美国).

1.2 MPE 修复模型设置

根据现有场地尺度模拟研究[9,11,18,23]，本研究以苯作为唯一污染物，建立了二维切片概念模型，模型尺寸及网格划分如图1 所示. 模型水平方向上长度为100 m，竖直方向上深度为15 m，厚度为1 m. 此外，模型上部设置高度为0.001 m 的网格作为大气边界，左右两侧设置水平长度为0.001 m 的网格作为定压水头边界. 模型网格均匀划分，在水平方向上以2 m 为单位长度划分网格，以最左侧作为相对水平距离等于0 m的原点；在竖直方向上以1 m 为单位长度划分网格，将地下水埋深位置作为相对深度等于0 m 的原点. 模型顶部相对深度为5 m，表示其位于地下水位线以上5 m；模型底部相对深度为——10 m，表示其位于地下水位线以下10 m. 模型网格总数为832 个，按照由左至右、由下往上的方式逐行编号. 在场地内进行为期1 年的释放以模拟污染物的泄漏，并进行1 年的污染物迁移扩散模拟以设置污染物初始分布，并模拟了为期90 d的MPE 修复.

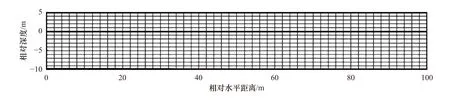
图1 模型尺寸与网格划分Fig.1 Model size and grid division

模型岩性设置中采用修正后的Stone 模型[27]描述场地相对渗透率，其方程形式如式(1)~(3)所示：

式中，krg、krw、krn分别表示气相、液相和NAPL 相的相对渗透率，krn′为修正后的近似NAPL 相相对渗透率，Sg、Sw、Sn分别为气相、液相和NAPL 相饱和度，Sgr、Swr、Snr分别为气相、液相和NAPL 相残余饱和度，A为拟合参数. 其中TMVOC 所需输入参数为Sgr、Swr、Snr以及A，本研究依照经验值和TMVOC 手册[23,28]分别取0.01、0.2、0.05 和3.

采用Parker 模型[29]描述三相系统的毛细压力，具体公式如式(4)~(7)所示：

式中：Sw、Sm、Sn分别为液相、残余相和NAPL 相饱和度；和分别为由式(4)和式(5)计算得到毛细管压力函数的斜率；Pcgn和Pcgw分别为气相-NAPL 相间毛细压力以及气相-水相间毛细压力，Pa；g为重力加速度，m/s2；αnw和αgn分别为气相-NAPL 相之间进气压力的倒数，以及NAPL 相和水相之间进气压力的倒数，1/Pa；B为Parker 模型的拟合参数；B′为计算过程的中间变量，数值上B′=1——1/B. 其中TMVOC 所需输入参数为Sm、B、αnw和αgn，本研究依照经验值和TMVOC 手册[23,28]分别取0.00、1.84、11.0 和10.0.

模型的水文地质参数、污染物设置参数与修复工艺参数取值范围参考了现有的TMVOC 研究[9,18,23,30-32]和TMVOC 手册[28]中案例所选取的参数范围以及工程经验. 对于岩性参数，现有文献报道[30-32]显示，土壤渗透率参数取值介于10——14~10——10m2之间，垂直渗透率为水平渗透率的0.25 倍；孔隙度随土壤渗透率的减小而增大，一般而言，黏土孔隙度为0.4~0.6，砂土孔隙度为0.3~0.4；岩层密度普遍采用2 600~2 700 kg/m3；常见的土壤其有机碳含量为0%~5%[33]. 其他参数中，抽提井真空度普遍取1×104~3×104Pa[9]，污染物释放速率普遍为10——6~10——5kg/s，降雨入渗设置可按照TMVOC手册[28].

本研究在上述范围内依照工程经验设定了模型参数，具体数值如表1 所示. 此外，为探究土壤渗透率对抽提修复和最优抽提井布设方案的影响，在此模型的基础上设定了8 种污染羽分布相同、土壤渗透率不同的场景模型，其水平渗透率参数取值分别为2×10——13、4×10——13、6×10——13、8×10——13、2×10——12、4×10——12、6×10——12和8×10——12m2，其余参数同表1.

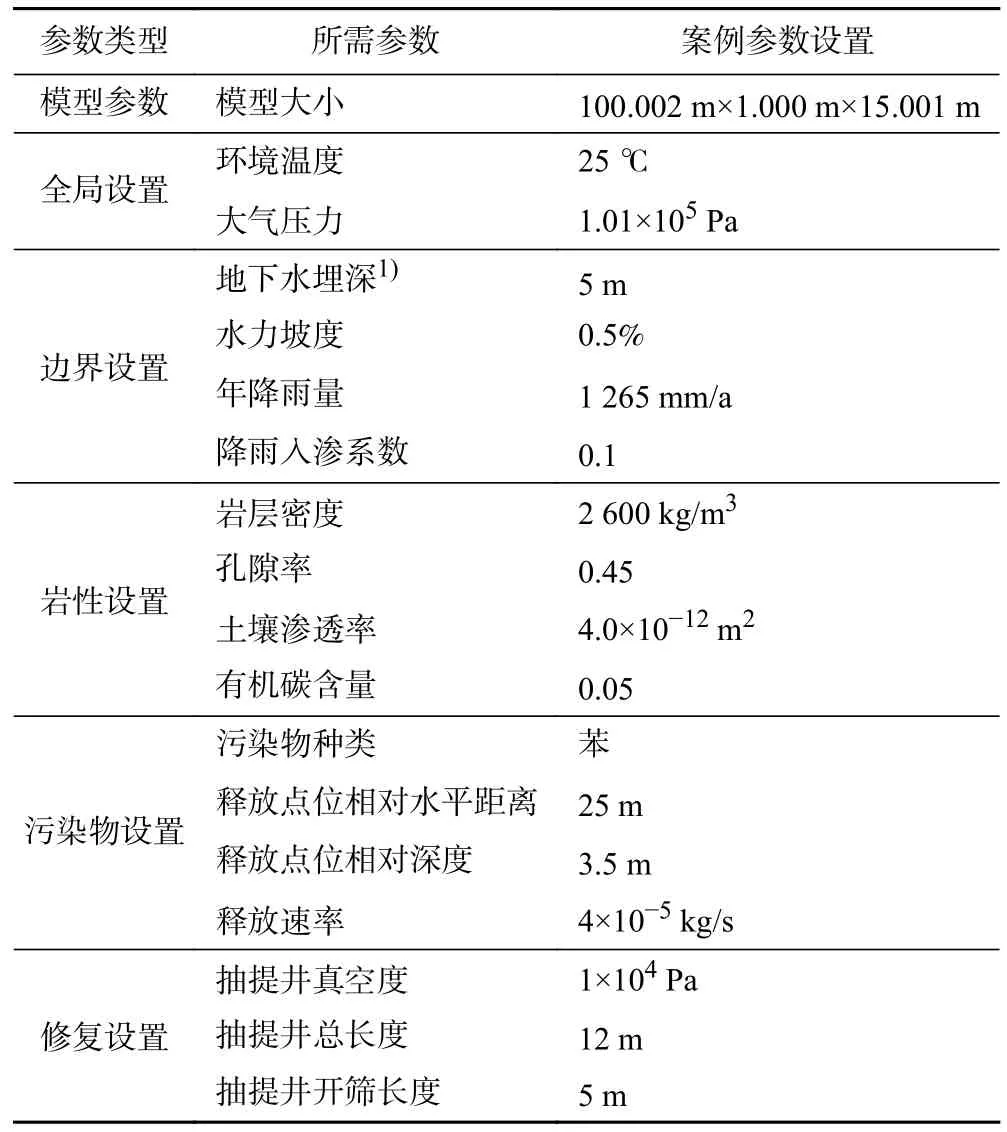
表1 模型中水文地质参数取值与修复工艺参数Table 1 Hydrogeological and remediation process parameters in the model

1.3 MPE 布井及开筛位置优化算法参数设置及约束条件

MPE 布井及开筛位置优化算法采用遗传算法，目标函数为抽提修复90 d 后的污染物去除率，分别以锦标赛选择法、单点变异和交换法实现种群的选择、变异和交换，群数大小设置为150，代沟为0.8，变异概率为0.01，迭代25 次[34].

TMVOC 所遵循质能平衡方程的形式如式(8)[28,35]所示：

式中：Va为流动单元体的体积，m3；Γa为表面积，m2；Mk为组分k在单位土壤介质中的质量，kg；Fk为进入流动单元体中组分k的总通量，kg；qk为组分k在单元体的源汇项，kg；a为流动区单元体表面的外法向单位矢量.

TMVOC 以GENER 模块描述特殊源汇项，其中同处一列的DELV 属性网格表示抽提井，因此设置抽提井位置时应当避开模型两侧及上方边界，故布井位置和开筛深度的约束条件可见式(9)~(12)：式中：ωc,i,j为第i口抽提井的开筛位置底部上方第j个网格在模型中的列位置；ωr,i,j为该网格在模型中的行位置；X和Z分别为模型总列数与总行数；L为设定的抽提井开筛长度对应的网格行数，本研究开筛长度为5 m，取5 行；Y为降雨入渗属性所占网格行数，数值取1.

1.4 经济性评估与碳排放量核算

本研究对成本计算和碳排放量核算方法进行了适当简化[13]，以定性分析各修复方案的成本和碳排放量. 以抽提井数量和深度评价施工成本，以抽提井运行过程中的电能耗为唯一因素核算运行成本及碳排放量[36]，计算方法如式(13)~(15)[13]所示，为评定最优修复方案，依据经验简单设定了式中变量的参考值以量化修复成本和碳排放量，在实际修复过程中，应当结合具体情况设定其数值.

式中：N为抽提井数量；θbu为建井施工成本，元；Di为第i口抽提井的钻井深度，m；kd为钻井深度费用系数，元/m，取经验值250 元/m；θbu′为其他施工成本，元，取1 000 元；θru为运行成本，元；Ei为第i口抽提井的每日能耗(kW·h/d)，与抽提井真空度和流量相关，为简化研究，假设每口抽提井每日能耗相同，统一取60 kW·h/d；θru′为其他每日运行成本，取1 000 元；T为达到修复目标值的时间，d；kE为能耗价格系数，即单位电价，以1 元/(kW·h)计；C为碳排放量，kg；kC为单位能耗碳排放量系数，kg/(kW·h)，取0.960 kg/(kW·h)[36].

2 结果与讨论

2.1 MPE 布井方案及开筛位置优化算法构建

利用MATLAB 搭建了基于TMVOC 与遗传算法的联合优化程序，利用程序代替了人工调参试错过程，输入文件改写和读取输出文件所用时间仅为0.8 s，相较人工设置参数可忽略不计；遗传算法的运用相较人工优化可以在有限的次数中确定最优布井位置. 其主要步骤包括建立输入文件与读取模型数据、参数集编码、修改输入文件、运行TMVOC 并读取模拟结果、优化结果计算.

2.1.1 建立输入文件与读取

使用MATLAB-TMVOC 优化程序前，先利用PetraSim 快速建立场地水文地质和污染物分布模型，基于该软件获得初始模型的TMVOC 输入文件，MATLAB-TMVOC 优化程序可以通过对该输入文件的改写和模拟实现优化过程.

根据TMVOC 用户手册，抽提井网格的参数被编写在输入文件的“GENER”(源和汇)模块中，该模块中每一行为一个网格所具有的源汇属性，共6 列，其中第1 列内容为对应的网格编号，同一列连续的网格被视作一口抽提井；第4 列为属性，其中DELV 为抽提井，COM1 常用作记录降雨入渗，COM2 则被设置为空气注入井；第5 列、第6 列分别为流量(曝气)和压力(抽提).

利用程序逐行读取文件后判定该行内容中是否存在“COM1、COM2、DELV”这三类TMVOC 中“GENER”模块的“源与汇”属性，最终记录下“GENER”模块的所有参数，计算模型中井数量以及网格数量.程序巧妙地利用了“COM1”入渗网格占据模型中一整行且上方仅存一行大气边界网格的原理，计算出了模型的总网格数、列数、行数. 总网格数计算公式：

式中，X为模型总列数， ∂MAX与 ∂MIN分 别 表 示 具 有“COM1”属性的网格的最大网格编号和最小网格编号.

因此总网格数为∂MAX与α之和，行数为总网格数与列数之商.

2.1.2 参数集编码

井网格的参数集确定及编码对遗传算法的运行至关重要. 依照TMVOC 将所处同一列连续的“DELV”属性网格判定为一口抽提井的原则，井网格参数集可以转化为每口抽提井最底部的井网格列编码和行编码.

显然对于井深度可以通过单井范围给定参数集，而对于井水平位置，可以采用“nchoosek”函数穷举所有列组合，然后通过选择组合的编号确定每口抽提井所在列.

2.1.3 修改输入文件、运行TMVOC 并读取模拟结果

在获得初始二进制编码转换的输入参数集后，修改输入文件，建立新的工艺参数下的修复模型，通过“system”函数调用TMVOC 便可以求解该模型，生成输出文件，读取输出文件中“TOTAL VOCs”模块内容的污染物残余量评价该参数的适应度.

2.1.4 优化结果计算

基于遗传算法对于不同的布井方案进行模拟以及优化迭代，最终确定最优布井位置. 利用MATLABTMVOC 优化布井方案及开筛位置可以有效地减少模拟时间和运算次数，优化程序可以自动化修改输入文件和读取模拟结果，所用时间可忽略不计，进行单次模拟的时长仅为TMVOC 模拟运行时长，约为70 s，而对于相同的模型，通过人工设置参数进行模拟的过程时长为120~180 s，自动化运行可以节省75%以上的单次模拟时间. 整个优化过程中，人工调参优化需要模拟尝试的次数具有不确定性，而遗传算法通过随机搜索可以在有限的次数中寻找到最优布井位置，快速高效的处理速度更有利于抽提井布设方案与开筛位置的优化.

在进行抽提井布设方案优化探究时，布设方案众多，本模型水平方向可选网格位置为50 种，最小布井间距为单元格水平距离2 m，竖直方向可选网格位置为9 种. 当布设5 口抽提井时，仅在水平方向有2 118 760〔C(50,5)〕种组合可能，但对于这种简单组合问题，遗传算法所需种群大小远小于参数集大小[11]，当遗传算法种群数为150 时，25 次迭代的运算过程中即可收敛获得最优解，总模拟次数为3 150 次，相较穷举所有可能性，计算量简化率超过90%.

2.2 不同MPE 抽提井数量方案的抽提井布点及开筛位置优化

通过PetraSim 模拟了污染物迁移释放及抽提修复过程并绘制了污染羽分布图，各井群数量下布井方案及开筛位置优化前后污染羽分布情况及去除率时间曲线见图2，在此基础上通过MATLAB-TMVOC联合程序优化了抽提井水平布置和开筛位置，经优化后的抽提方案可以于65 d 内达到90%的污染物去除率.

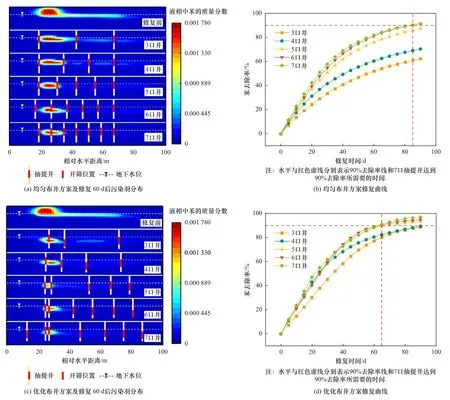
图2 优化前后修复60 d 后残余污染物分布及90 d 内污染物去除率变化Fig.2 Distribution of residual pollutants after 60 d and changes in removal rate within 90 d of remediation before and after optimization

均匀布井修复前后污染与分布和去除率情况如图2(a)(b)所示. 修复前的初始污染羽水平长度约为58 m，竖直长度约为6 m，超过50%的污染物处在模型相对水平位置17~34 m 处，即污染源附近形成了一个污染核心区域，该区域内地下水中的污染物浓度超过其他区域2 倍. 本研究设置了不同数量的抽提井群，分别以24、16、12、10、8 m 的间隔均匀布设抽提井以保证污染物的去除，抽提井开筛位置根据核心区域污染物分布情况设置，筛管底部的相对深度设置为——4 m，筛管顶部的相对深度设置为1 m，具体布井点位如表2 所示. 在90 d 的修复周期内，随着布井数量由3 口增至7 口，污染物去除率由58.5%增至89.2%，修复效率增加了52.4%. 均匀布设间距为8 m 的7 口抽提井可以在93 d 达到90%的去除率.

表2 优化前后的抽提井位置布设Table 2 Layout of extraction well positions before and after optimization

利用MATLAB-TMVOC 联合优化程序优化了不同数量井群的布井方案和每口井的开筛位置，其中开筛长度统一为5 m，优化后修复前后残余污染物的分布和去除率情况如图2(c)(d)所示，在污染物去除率上，90 d 的周期内，7 口抽提井MPE 修复方案的污染物去除率可达97.0%，相比优化前提高了7.9%，优化前7 口抽提井需要93 d 才能达到90%的污染物去除率，而优化后7 口抽提井在63 d 内即可达到目标修复值，缩短了30 d 的修复时间，优化方案提升了32.9%的修复速率.

优化后布井方案及开筛位置如表2 所示，在布井规律上，相较均匀布井，优化后的抽提井排布是根据污染物浓度及抽提井数量设计的非等间距布点，随着污染羽的分布，在水流方向上由密至疏，抽提井的数量在4 口以上时，位于核心区域的两口抽提井间距缩小至2~4 m，而污染羽尾部低浓度区抽提井间距为10~20 m，这与王颖[9]对于多个低渗透场地SVE 模拟修复结果相近，当抽提真空度为10 kPa 时，单井的影响半径为3.5~16 m. Sookhak 等[11]利用遗传算法与TMVOC 的并行版本TMVOC-MP 相结合研究了多相抽提修复某低渗透性污染场地的平面布井模型，得到了相同的结论，均匀布井并非是最优布井方案. 当抽提井开筛长度固定为5 m 时，最优布井方案的开筛位置在水平方向上深度逐渐增加，在污染羽核心区域，即污染羽前段，筛管顶部相对深度为1 m，略低于污染羽，修复以多相抽提为主，随着污染羽核心区域水平距离的增加，筛管顶部相对深度为0 m，以液相抽提为主，这是因为污染物主要通过地下水流动而发生横向迁移，下游区域主要为液相LNAPL[37-38]. 田蕾等[23]探讨了低渗透场地中抽提井开筛位置深度对于污染物去除率的影响，得到了相同的结论，当抽提井开筛位置最底端降至NAPL 附近时，修复效率最高，达到90.4%，而仅对包气带进行抽提时，去除率仅为29.1%. de Souza 等[17]通过STOMP 探究了MPE 修复过程中抽提井底部的最佳位置，结果显示，当开筛位置底端高程从14 m 提升至17 m 的过程中，最佳修复位置位于15.8 m 处，为气相-NAPL 与液相-NAPL 交界面之间. 这些研究结果都显示，MPE 抽提井开筛位置最底端应当低于地下水位，对于NAPL 和地下水直接的抽提有利于污染物的去除. 4 种优化布井方案都选择相对水平距离25 m 处(污染物释放点)布设筛管底部深度为地水位线下3~4 m 的抽提井，可见此处是污染物MPE 修复的关键布井点，在实际场地布设抽提井时，应当重点关注污染源，布设抽提井群中的主井.

2.3 不同MPE 抽提井数量修复方案的修复成本和碳排放量核算

当污染物目标去除率为90%时，不同抽提井数量下优化前后MPE 修复成本及碳排放量核算结果如表3 所示，优化前，6 口抽提井修复运行成本、总成本及总碳排放量(能耗)最低，分别为12.9×104元、14.8×104元与32.9 t，而5 口抽提井的总碳排放量最高，能耗最高. 优化后6 口抽提井运行成本最低，为8.4×104元；5 口井的总成本与碳排放量最低，分别为10.2×104元与19.6 t，盲目地缩小布井间距、增加抽提井数量会导致修复效率低，运行成本高. 相比优化前，优化后的方案可以节约29.7%~34.7%的运行成本、22.7%~29.3%的总成本以及21.4%~40.4%的碳排放量，MATLAB-TMVOC 联合优化后的抽提方案能够有效提高抽提效率，具有绿色、低碳和高效的特点.

2.4 不同渗透率场地中6 口MPE 抽提井修复方案的布井位置优化

2.2 节分析结果显示90 d 内6 口抽提井MPE 修复方案对土壤渗透率为4×10——12m2的模拟场地的污染物去除率可达90%，因此本节基于1.2 节构建的污染场地模型和污染羽分布，模拟了不同渗透率场地下6 口抽提井的MPE 修复过程，并利用MATLAB-TMVOC优化程序探究最优抽提井布井方案规律.

优化前后不同土壤渗透率下6 口抽提井布井方案的布井点位水平位置和开筛位置如表4 所示. 优化前的布井方案为均匀布设，具体点位同2.2 节中6 口抽提井均布方案，根据污染羽分布情况，以10 m 为间隔设置了均匀布井方案，筛管底部深度位于地下水位线下4 m；优化后的布井方案为非均匀的布井方案，与2.2 节相似，位于核心区域的抽提井间距较短，为2~4 m，而污染羽尾部低浓度区抽提井间距较长，为10~20 m. 优化布井方案随土壤渗透率的降低而发生改变，在土壤渗透率由8×10——12m2降至2×10——13m2的过程中，6 口抽提井的布井位置逐渐向污染物核心区域移动，6 口井首尾距离由71 m 缩短至44 m，平均井间距由11.8 m 降至7.3 m，降低了38%. 4 口靠近污染羽核心区域(水平位置15~50 m)的抽提井的平均间距由10.5 m 降至5.5 m，减少了47.6%. 优化后的布井平均间距与土壤渗透率呈正相关，当土壤渗透率处在10——12~10——13m2范围内，土壤渗透率每减少10——13m2，优化后的抽提井间距会减小约0.13 m，即当土壤渗透率下降一个数量级时，抽提井间距应减少17.8%~48.3%.

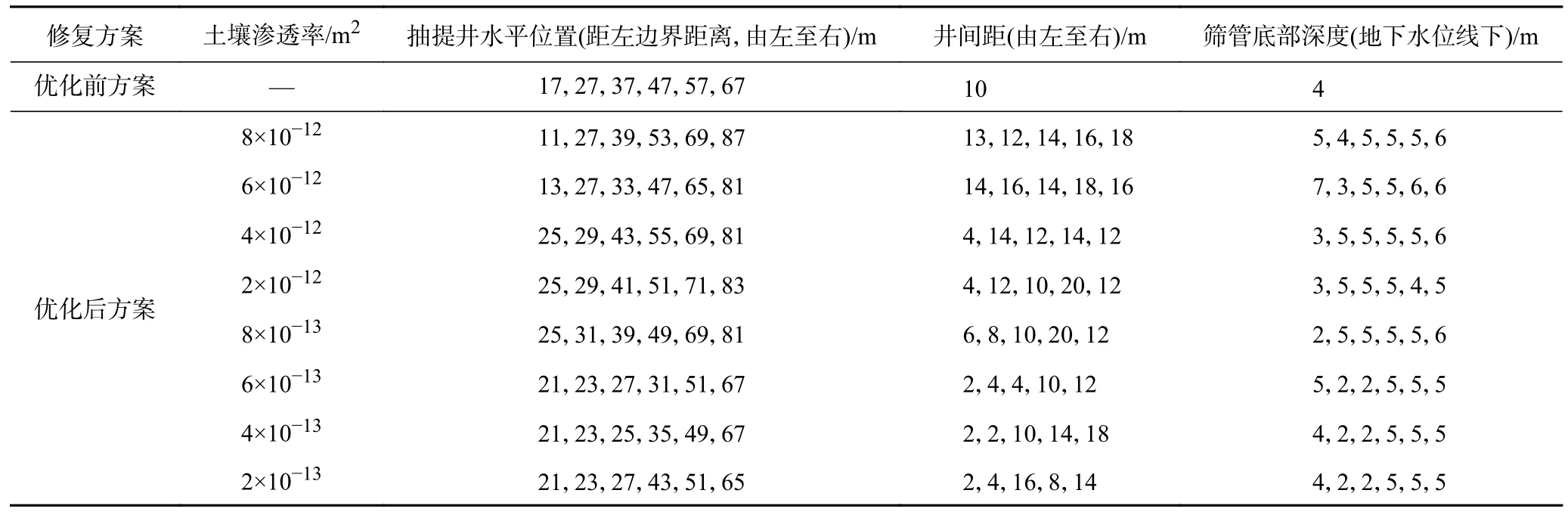
表4 优化前后不同渗透率下的抽提井位置布设Table 4 Layout of extraction well positions for different permeability rates before and after optimization

优化前后不同土壤渗透率下6 口抽提井的布井方案与修复60 d 后污染羽分布如图3(a)(b)所示，污染羽分布变化显示，污染物修复效果随土壤渗透率的降低而减小，以土壤渗透率为8×10——12m2的模拟场地的均匀布井修复结果为例，经60 d 的MPE 修复后污染羽水平相对位置由17~80 m 范围内缩小至20~30 m范围内，相对深度位于包气带的污染羽发生消失；而当土壤渗透率为8×10——12m2时，经均匀布井修复60 d后的污染羽大小几乎不变，包气带仍存在大量污染物. 对比结果表明，优化后的方案较优化前可以缩小修复后的污染羽范围，以土壤渗透率为8×10——12m2的场地为例，相同比例尺下，优化前仍有少部分可见污染羽，而优化后几乎未见污染羽分布.

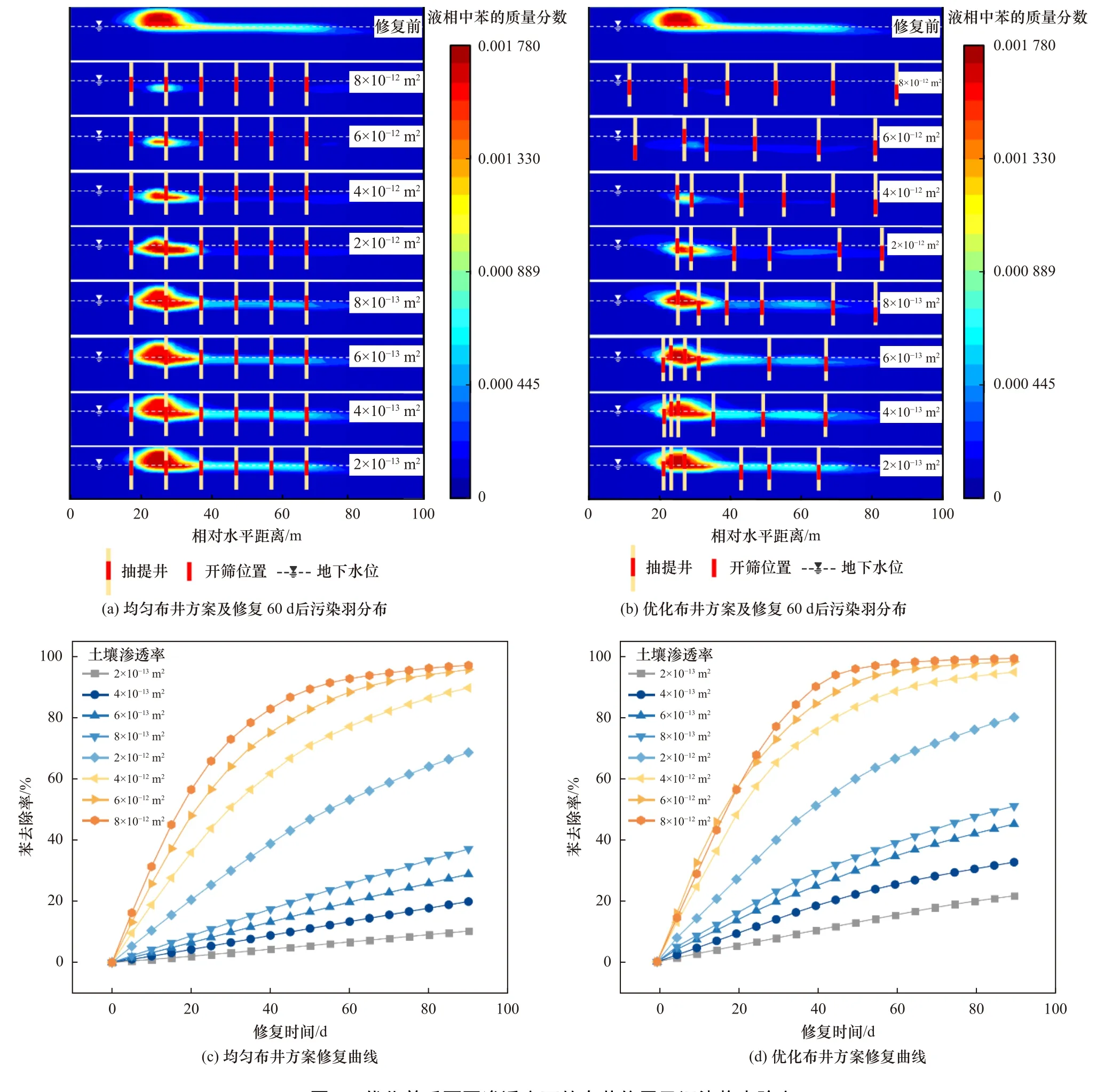
图3 优化前后不同渗透率下的布井位置及污染物去除率Fig.3 Well location and pollutant removal rates before and after optimization for different permeability conditions

优化前后不同土壤渗透率下修复过程中苯去除率随时间的变化曲线如图3(c)(d)所示，随着土壤渗透率由8×10——12m2降至2×10——13m2，均匀布井方案的污染物去除率由97.1%降至10.2%，而优化布井方案的污染物去除率由99.2%降至21.5%，优化后的布井方案可以提升污染物修复效果，各土壤渗透率下MPE修复污染物去除率大于均匀布井方案，土壤渗透率处于2×10——13m2~8×10——12m2范围时，优化后的修复方案可使污染物去除率增加2.1%~16.2%. 王颖[9]利用TMVOC模拟了15 个土壤渗透率介于10——14~10——12m2之间的场地模型中的苯系物泄漏、迁移以及SVE 修复过程，15 个模型除土壤渗透率外水文地质参数相近，苯泄漏速率均设置为2×10——5kg/s，泄漏与扩散时间均为1 年，在布井间距为7.5~10 m、抽提真空度为1×104Pa 的等间距布井方案下经SVE 修复2 年，污染物去除率为9%~99%；其中包气带土壤渗透率为1×10——12m2与9×10——13m2的场地，经SVE 修复后污染物去除率分别为60%与50%. 本研究中场地土壤渗透率为2×10——12m2与8×10——13m2的场景经优化后布井方案修复后，180 d 内的污染物去除率分别达到90%与60%. 对比显示，在土壤渗透率、污染物羽分布和抽提真空度相似的条件下，基于MATLAB-TMVOC 联合优化程序设计的方案可以显著提升污染物的修复效率.

总体而言，当土壤渗透率大于2×10——12m2时，最小布井距离为4 m，90 d 内污染物去除率高于90%，当土壤渗透率处于10——13m2数量级时，污染物去除率低于60%，最小布井间距达模型布井间距下限(2 m)，为达到90%的去除率，应当增加抽提井数量或修复时间. 这是因为土壤渗透率的降低会使流体流动能力减弱，使得污染物向气相、液相的迁移能力降低，从而使得抽提效率降低，抽提井有效影响半径减小[39].

2.5 不确定性分析

本研究以数值模拟的方式探究MPE 修复抽提井布设的优化方案，其结果具有不确定性，主要体现在两个方面：①在优化效果上，虽然2.2 节与2.4 节的模拟结果显示，优化后的方案相较优化前的均匀布井方案，能够提升2.1%~32.9%的修复效率，但是单一遗传算法的应用存在产生局部最优解的可能，优化后方案可能并非全局最优布井方案，需要结合诸如改进遗传-模拟退火算法等联合算法的应用以降低遗传算法发生“早熟”的可能[40]. ②研究模型仅为理想化的二维切片，在模型构建和经济及碳排放评估过程中选取的部分参数存在理想化和简化，对计算结果存在影响. 薛成杰等[36]的研究结果显示，使用气相抽提等土壤原位修复技术修复1 m3土壤的成本为500~1 000元，修复1 t 土壤的碳排放量为40~400 kg，以此参数计算本场地的修复成本与碳排放量，可知2.2 节场地的修复成本为2×105~4×105元，碳排放量为23~230 t，该结果均存在一定程度的低估，主要原因在于，为简化分析，本研究仅以抽提井运行过程中的电能耗为唯一因素核算运行成本及碳排放量. 但实际上多相抽提工艺中诸如管理等诸多环节都涉及碳减排潜能，特别是对于抽提尾气处理环节，需要对收集抽提尾气的活性炭进行无害化处理，该过程也是MPE 修复中重要的碳排放源[36].

3 结论

a) 本研究建立的MATLAB-TMVOC 优化程序，能够有效联合TMVOC 与优化算法，自动化实现MPE 修复模拟，免除数值模拟繁重的人工调参过程，缩短单次模拟的时间，在有限的计算模拟次数中高效求解最优布井方案.

b) 多相抽提井布设间距应当随着土壤渗透率的降低而缩小，当土壤渗透率处在10——13~10——12m2范围时，抽提井间距与渗透率成正比. 使用MPE 技术修复土壤渗透率低于10——13m2的黏性地层时，场地污染羽核心位置的布井间距应当小于4 m.

c) MPE 布井方案和抽提井开筛位置经优化后，可以减少抽提井数量并缩短修复时间，节约29.7%~34.7%的运行成本，降低22.7%~29.3%的总成本，减少21.4%~40.4%的碳排放量，实现污染场地修复的低碳减排.