无网格法结构拓扑优化模型的GPU 并行加速求解及应用

唐 芳，冯应朗，卢海山

（1.湖南理工职业技术学院新能源学院，湖南 湘潭 411105；2.湘潭大学机械工程与力学学院，湖南 湘潭 411105）

0 引言

结构拓扑优化技术可在产品的概念设计阶段提供创新设计方案，现已广泛应用于汽车、航空航天以及增材制造等领域[1，2]。目前结构拓扑优化一般利用有限元法进行结构分析，然而由于单元的存在，使得基于有限元法的结构拓扑优化模型容易出现棋盘格、单元铰接等数值不稳定现象[3]，且在处理大变形、含裂纹结构的拓扑优化问题时，面临网格畸变、不连续等困难[4]。

无网格法仅需离散节点信息即可构造出高阶场函数，并能有效处理大变形、不连续等问题。部分学者将无网格法引入结构拓扑优化，利用无网格不受网格束缚的优势，有效克服了传统基于有限元法的拓扑优化模型存在的缺点[5]。无网格Galerkin（Element-Free Galerkin，EFG）法是当前成熟且应用广泛的无网格法之一，具有收敛快、计算精度高和稳定性好等[6]优点，在结构拓扑优化中得到应用[7]，有效地抑制了传统拓扑优化中所出现的棋盘格等数值不稳定现象，同时避免了大变形结构拓扑优化中的网格畸变。

尽管基于无网格法的拓扑优化模型具有上述优势，但由于拓扑优化的求解需要多次迭代，重复进行结构分析计算，并且无网格法的计算量大，导致拓扑优化模型的求解极其耗时，难以应用于大规模拓扑优化问题。

近年来，GPU 并行加速技术因其强大的并行计算能力在计算力学领域得到广泛应用。韩琪等[8]针对大规模拓扑优化问题计算量大、计算效率低的问题，结合双向渐进结构拓扑优化方法与GPU 并行加速计算技术，设计了一种并行拓扑优化方法；Xia 等[9]等提出了一种使用GPU 并行策略与等几何分析的水平集拓扑优化方法，加速比达到两个数量级。而在无网格法的GPU 并行加速研究方面，龚曙光等[10]通过并行化组装刚度矩阵与求解离散方程，并为了充分发挥FEM 与EFG 法各自的优势，提出了FE-EFG 耦合法的GPU 并行加速算法。

针对无网格法结构拓扑优化模型的求解计算存在耗时长的问题，结合GPU 并行加速技术，提出了一种求解EFG 法拓扑优化模型的高效计算方法。该研究对无网格法应用于工程结构拓扑优化设计具有重要的理论意义与参考价值。

1 EFG 法拓扑优化模型

1.1 EFG 离散方程

位移u（x）的移动最小二乘逼近函数uh（x）为：

式中，N为节点数；U为节点位移参数列阵；Φ（x）为形函数矩阵，且其计算式为：

式中，A和H分别表示一个矩阵，并有

其中

式中，pm（xN）为基函数；w（x-xI）为权函数。本文采用线性基函数和三次样条权函数。

利用罚函数法施加本质边界条件，可得线弹性静力问题的EFG 离散方程：

式中，K为刚度矩阵；F为节点力向量；B为应变矩阵；α为罚系数；D为弹性矩阵。

1.2 拓扑优化模型及迭代更新

选择节点相对密度参数ρi作为设计变量，则设计域内任意点的相对密度ρ（x）可由移动最小二乘逼近得到

利用变密度法中的各向同性材料惩罚模型（SIMP）计算优化后的材料弹性模量为

式中，E0为实体材料的弹性模量，p为惩罚因子。

以结构柔度为目标函数、材料体积为约束条件，建立如下拓扑优化数学模型

式中，V0、V分别为优化前后的结构体积；ζ为体积保留率。

本文采用OC 准则法求解上述优化模型，其设计变量的更新格式为

式中

2 GPU 并行加速算法

2.1 CUDA 架构

NVIDA 推出的CUDA 平台，极大地简化了GPU并行编程。在CUDA 平台下，并行程序的执行模式为：①在CPU 的内存中准备好数据，并复制到GPU的显存中；②GPU 执行设备端程序；③将计算结果传回CPU 中的内存。GPU 上执行核函数的最小单位为线程，CUDA 将多个线程组成为一个线程块，多个线程块则构成为一个线程格。线程组织及存储器的架构如图1 所示。

图1 CUDA 的线程组织及存储架构

2.2 刚度矩阵计算

基于交叉节点对（影响域有交集的两个节点）的思想，提出了一种通过交叉节点对的循环来计算刚度矩阵的逐节点对法[18]。本文借助交叉节点对思想，结合上述CUDA 架构特点，构建了利用GPU 并行加速拓扑迭代过程中刚度矩阵的并行计算流程，如图2 所示。该并行流程有两个并行层次：第一个层次是交叉节点对，即每个线程块处理一个交叉节点对，第二层次是交叉节点对的公共积分点，即线程块中的每个线程处理交叉节点对的一个公共积分点。与公共积分点相关的数据存储于对应线程的寄存器，与交叉节点对相关的数据储存在线程块的共享内存，而最终的刚度矩阵储存在GPU 的全局内存。

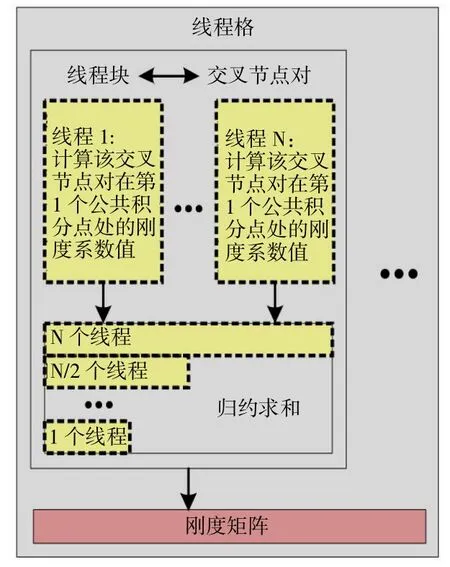
图2 刚度矩阵的GPU 并行计算

2.3 离散方程求解

结构拓扑优化模型的优化迭代过程需要对EFG法形成的离散方程进行重复求解，以获得结构响应。由于直接法所需内存大、矩阵分解耗时长，同时由于材料分布的高度非均匀性导致形成的EFG 刚度矩阵条件性态差，为了提高平衡方程的求解效率，本文采用雅克比预处理共轭梯度法，并结合GPU 并行加速技术求解离散方程，其计算流程如下：

其中，J为雅克比预处理矩阵。

2.4 GPU 并行加速流程

无网格法拓扑优化模型的GPU 并行加速求解流程如图3 所示。在该流程中，耗时量最大的计算刚度矩阵与求解离散方程两个部分在GPU 并行计算，而其余耗时很少的部分则在CPU 串行计算。此外，由于每一次OC 迭代均需要利用形函数及其导数值重新计算刚度矩阵，为避免反复计算形函数及其导数值，在前处理计算部分提前完成形函数及其导数值的计算并存储至GPU 全局内存，从而进一步降低计算耗时。

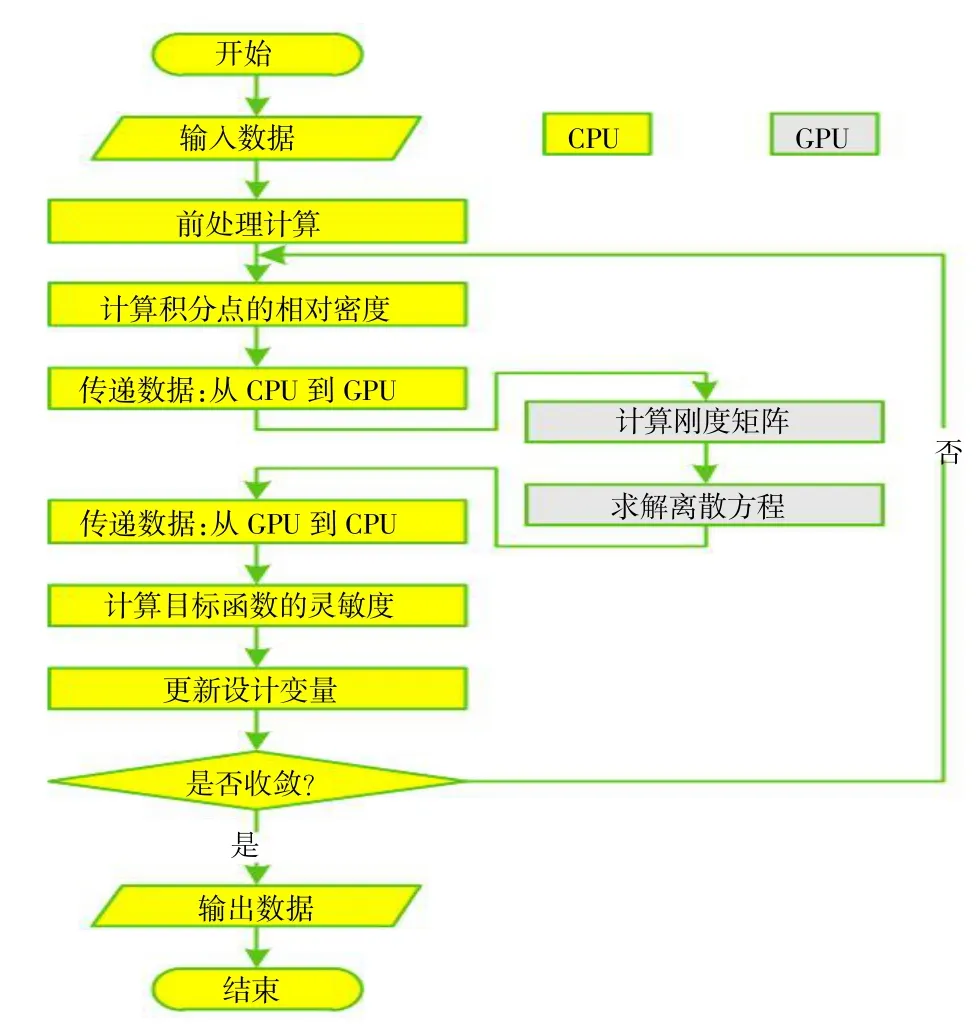
图3 GPU 并行加速流程

3 数值算例

在算例中，材料的弹性模量为E0= 1.0，泊松比为v= 0.3。算例的运行平台配置参数见表1。

表1 运行平台配置参数

定义加速比为

式中，tCPU为CPU 串行算法的运行耗时，tGPU为GPU 并行加速算法的运行耗时。

3.1 二维悬臂梁

图4 为悬臂梁模型。其中L= 90 mm。悬臂梁左边界为固定约束，右边中点承受竖直向下的集中力F=1 N。设计域的体积保留率为ζ= 0.1。

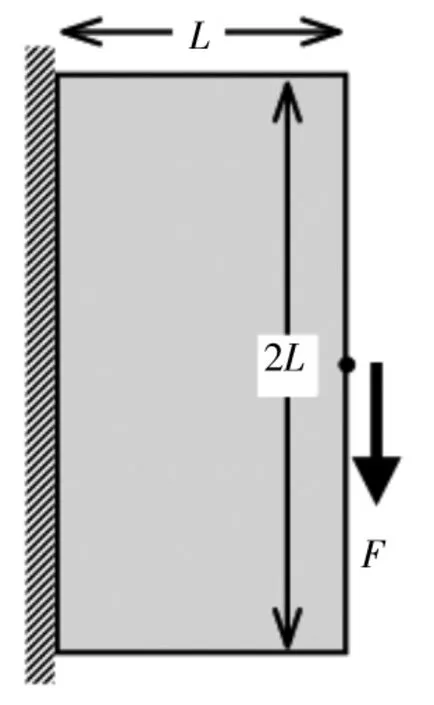
图4 悬臂梁

悬臂梁的拓扑优化结果如图5 所示。从图5 可知，CPU 串行程序的拓扑结果与GPU 并行加速程序的拓扑结果完全吻合，且拓扑结果边界清晰，无棋盘格等数值不稳定现象。这表明上述无网格拓扑优化模型及其GPU 并行加速求解算法是正确的。

图5 悬臂梁的拓扑结果

采用数目分别为1891（31×61）、7381（61×121）、29161（121×241）与115921（241×481）的四组节点离散该悬臂梁模型。四组节点规模下CPU 串行程序的各段耗时及比例见表2。由表2 可知，求解方程耗时占据了整个CPU 串行程序耗时的大部分，其次是计算刚度矩阵的耗时，而程序其余部分耗时的占比极低，表明CPU 串行算法的性能瓶颈主要在求解方程与计算刚度矩阵两个部分。因此，利用GPU 并行加速刚度矩阵计算与方程求解，就能够有效提高拓扑优化模型的求解效率，且能够避免在内存与显存之间反复传输刚度矩阵等大量的数据，从而进一步提高拓扑优化模型的求解性能。

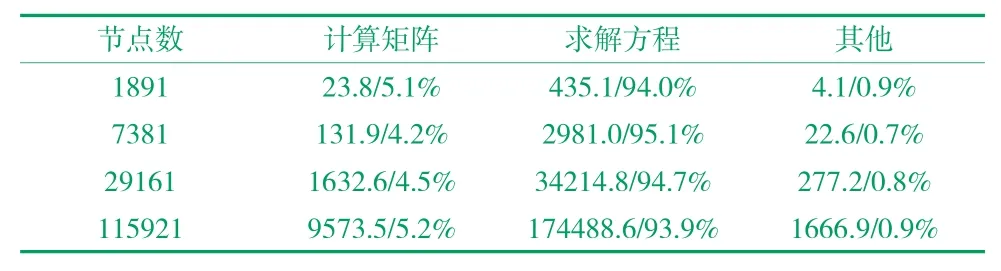
表2 CPU 串行程序的各段耗时（s）及比例

四组节点规模下GPU 并行算法对CPU 串行算法的加速比如图6 所示。由图6 可知，当节点规模较小时，整体加速比随节点规模增大而增加，但当节点规模增大到一定数量后，加速比出现小幅降低。这是由于GPU 的并行线程及寄存器与共享内存等资源是有限的，即GPU 能同时并行计算的任务量有限。方程求解加速比与整体加速比的变化趋势较为一致，但当节点规模较大时，加速比增幅减小。刚度矩阵计算加速比随节点规模增加呈现先小幅增加而后又小幅降低的趋势。这表明求解离散方程的加速性能在整个拓扑优化模型的加速求解过程中起主导作用。此外，该算例结果表明GPU 并行加速算法对于规模较大的无网格法拓扑优化模型的求解具有更加显著的加速效果。

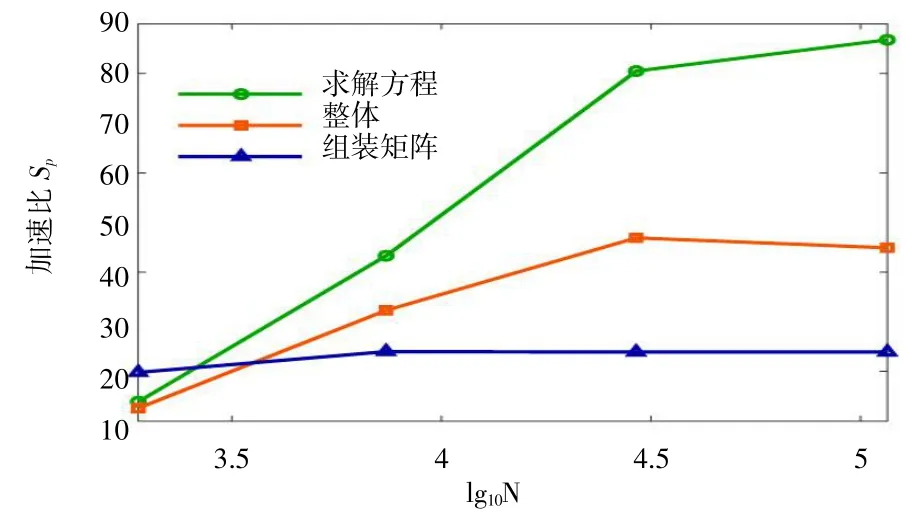
图6 不同节点数的加速比

3.2 二维曲形支架

图7 为曲形支架模型。结构尺寸为R= 100 mm、r= 50 mm。支架右边顶点承受水平向左的集中力F=1 N，支架底边施加固定约束。设计域的体积保留率为ζ= 0.5。采用8320 个节点离散该设计模型。由图8 可知，CPU 与GPU 程序的拓扑优化结果完全一致。

图7 曲形支架

图8 曲形支架的拓扑结果

计算耗时及加速比如图9 所示。CPU 程序总耗时高达13371.5 s，而GPU 程序总耗时仅为400.9 s，加速比达33.4，表明了本文GPU 并行加速算法的强大并行加速能力。

图9 曲形支架的计算耗时及加速比

3.3 三维支撑平台

图10 为三维支撑平台模型。结构尺寸如图11 所示。该支撑平台由顶部平板与下方的锥形筒体组成。平台顶面中心承受竖直向下的集中力400 kN，平台底面均匀分布四处固定约束。该模型具有对称性，可取整体模型的四分之一，得到平台的优化设计分析模型，如图12 所示。其中，平台顶部的平板（图12 中的灰色区域）划分为非设计域，在优化过程中，该部分的材料保持不变，以便于承受载荷。设计域的体积保留率为ζ= 0.2。采用13476 个节点离散该设计模型。

图10 支撑平台

图11 支撑平台模型尺寸（mm）

图12 支撑平台设计模型

拓扑优化结果如图13 所示，该拓扑结果合理、清晰，无棋盘格等现象。这是由于采用移动最小二成逼近构造的密度场具有高阶连续性，从而有效地抑制了棋盘格等数值不稳定现象。此外由于划分了非设计域，支撑平台顶部的平板被保留，因此得到的最优结果便于承受载荷，满足使用要求。

图13 支撑平台的拓扑结果

支撑平台算例的计算耗时及加速比，如图14 所示。CPU 程序总耗时为11235.1 s，而GPU 程序总耗时为518.0 s，加速比达21.7，表明了GPU 并行加速算法对于三维结构拓扑优化问题同样具有很好的加速求解性能。

图14 支撑平台的计算耗时及加速比

3.4 多工况固支梁

多载荷工况拓扑优化问题的每步OC 迭代过程均需要多次求解离散方程，以获得不同载荷工况下的结构响应，这将进一步增加计算耗时。本文利用GPU并行加速算法求解多工况固支梁优化模型，以测试GPU 算法对多载荷工况拓扑优化问题的加速求解性能。图15 为二维多工况固支梁模型，结构尺寸如图15 所示，其中L= 90 mm。固支梁的左右两端固定，顶边和底边中点处分别承受竖直向下与向上的集中力与。设计域的体积保留率为ζ= 0.3。采用10011 个节点离散该设计模型。图16 所示的CPU 与GPU 程序的拓扑优化结果完全吻合，进一步验证了本文所建立的GPU 并行加速求解算法的正确性。

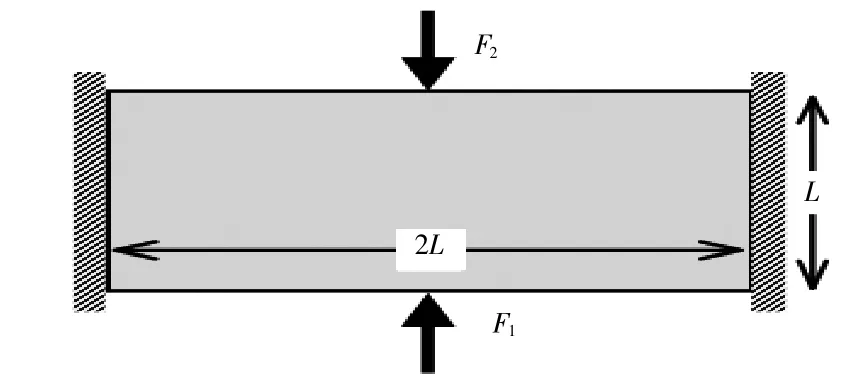
图15 多工况固支梁

图16 多工况固支梁的拓扑结果

图17 给出了多工况固支梁算例的计算耗时及加速比。CPU 程序总耗时为9383.3 s，GPU 程序总耗时为307.6 s。尽管在两个载荷工况下每一次OC 迭代均需要求解两次离散方程，但GPU 程序的耗时仍然远远小于CPU 程序耗时，且加速比达到了30.5。

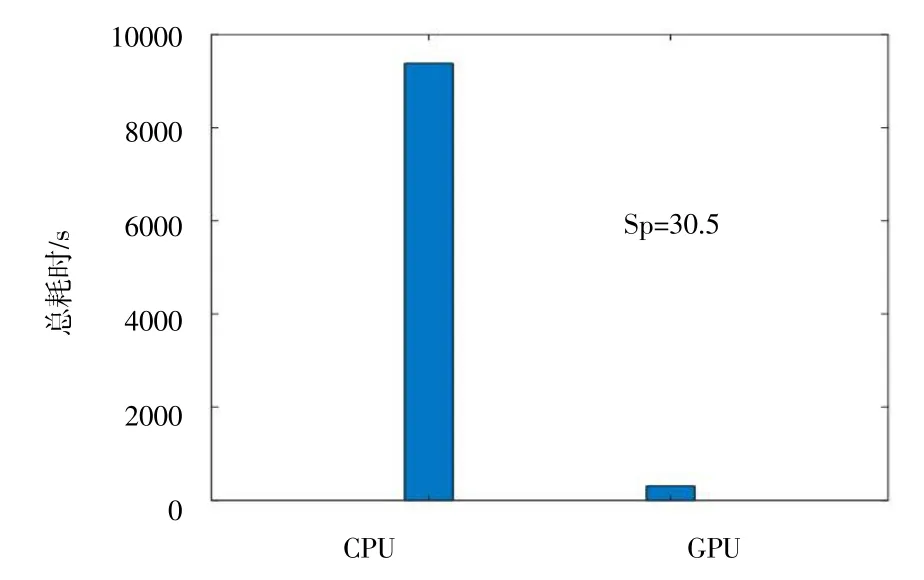
图17 多工况固支梁的计算耗时及加速比

4 结语

针对无网格法结构拓扑优化模型求解计算耗时长的问题，通过引入GPU 并行加速技术建立了无网格法拓扑优化模型的并行加速求解算法，以充分发挥无网格法不受网格束缚、GPU 并行加速计算效率高的优势。经算例分析得到了如下结论：

（1）无网格拓扑优化模型的GPU 并行加速求解算法的拓扑结果与CPU 串行算法的拓扑结果完全吻合，所得到的最优拓扑构型清晰，无棋盘格等数值奇异问题。同时，在结构中划分了非设计域，非设计域内的材料在优化迭代过程中均保持为实体材料，所得到的拓扑结构更为合理，满足使用要求。

（2）算例的整体加速比最大可达46.9，表明所提无网格拓扑优化模型的GPU 并行加速求解算法具有优良的加速性能。且当计算规模较大时，加速效果更加显著，但受限于GPU 自身的计算资源，加速比存在上限。

（3）尽管多载荷工况拓扑优化问题的每步OC 迭代均需要多次求解离散方程，但相比于CPU 串行算法，GPU 并行加速算法仍能大幅缩短拓扑优化模型的求解耗时，表明所提出的GPU 并行加速算法对于多载荷工况的拓扑优化问题同样具有很高的求解效率。