Effects of potassium channel blockage on inverse stochastic resonance in Hodgkin-Huxley neural systems

Xueqing WANG,Dong YU,Yong WU,Qianming DING,Tianyu LI,Ya JIA

Department of Physics,Central China Normal University,Wuhan 430079,China

Abstract: Inverse stochastic resonance (ISR) is a phenomenon in which the firing activity of a neuron is inhibited at a certain noise level.In this paper,the effects of potassium channel blockage on ISR in single Hodgkin-Huxley neurons and in small-world networks were investigated.For the single neuron,the ion channel noise-induced ISR phenomenon can occur only in a certain small range of potassium channel blockage ratio.Bifurcation analysis showed that this small range is the bistable region regulated by the external bias current.For small-world networks,the effect of non-homogeneous network blockage on ISR was investigated.The network blockage ratio was used to represent the proportion of potassium-channel-blocked neurons to total network neurons.It is found that an increase in network blockage ratio at small coupling strengths results in shorter ISR duration.When the coupling strength is increased,the ISR is more significant in the case of a large network blockage ratio.The ISR phenomenon is determined by the network blockage ratio,the coupling strength,and the ion channel noise.Our results will provide new perspectives on the observation of ISR in neuroscience experiments.

Key words: Inverse stochastic resonance (ISR); Small-world neuronal network; Potassium channel blockage; Network blockage ratio

1 Introduction

It was widely believed that adding noise (Faisal et al.,2008; Jin et al.,2019; Yu et al.,2021,2022a) to the transmission of information by neurons (Ma,2023)tended to have a negative effect.However,a counterintuitive effect (stochastic resonance) (Liu and Li,2013)allows the non-linear system to obtain the maximum response to the signal at the appropriate noise level(Gluckman et al.,1996; Gailey et al.,1997; Perc,2007;Wang et al.,2009; Kawaguchi et al.,2011).This means that proper noise can improve the efficiency of information transmission and processing by amplifying the neuron’s response to the signal (Chik et al.,2001;Kosko and Mitaim,2003; McDonnell and Abbott,2009).In addition,noise has an inhibitory effect on neuronal activity.In experiments on the in-vitro preparation of squid axons,Paydarfar et al.(2006) found that small noise could inhibit neuronal pacemaker activity and induce switching behaviour between repetitive firing and resting.Gutkin et al.(2009) and Tuckwell et al.(2009) studied the role of noise on the firing rhythms of Hodgkin-Huxley (HH) neurons (Hodgkin and Huxley,1952a).The results showed that a minimum of neuronal firing activity occurred at moderate noise levels.This phenomenon is referred to as inverse stochastic resonance (ISR).

In recent years,ISR has been extensively researched and proved both experimentally and theoretically.On one hand,Buchin et al.(2016) found that a noise of specific amplitude in cerebellar Purkinje cells can effectively suppress spike generation,thus providing the primary experimental evidence for ISR.Huh(2016) reported that ISR can be observed in alternating current-driven electrical convection in nematic liquid crystals.On the other hand,Uzuntarla et al.(2013) investigated channel noise-induced ISR in HH neurons,demonstrating that ISR depends on the setting of the initialization time in the simulation.They also elucidated the mechanism behind ISR from the perspective of kinetic structure.Furthermore,the ISR with specific biophysical mechanisms was discussed.It was found that ISR is related to synaptic input mechanisms(Uzuntarla,2013),and ISR is most significant when excitatory and inhibitory synaptic currents are in relative balance.Further,the authors reported on the dual ISR (Uzuntarla et al.,2017a) induced by dynamic synapses and the more complex kinetic mechanisms behind it.In addition to ISR induced by ion channel noise,other noises can also induce ISR effects.It is found that Gaussian colored noise (Lu et al.,2020),non-Gaussian colored noise (Li et al.,2018),and Levy noise (Zhao and Li,2019; Li et al.,2020) can also induce ISR effects (Wang et al.,2022).ISR has been further extended to neuronal networks (Uzuntarla et al.,2017b).

During the generation of action potentials in neurons (Wu et al.,2018; Zhang and Ma,2021; Yu et al.,2022b,2023a,2023b),the distribution of ion channels is one of the important influencing factors.Tetraethylammonium (TEA) and tetrodotoxin (TTX) can reduce the numbers of open potassium channels and sodium channels,respectively (Narahashi and Moore,1968;Hoyt and Strieb,1971).Schmid et al.(2004) investigated the effect of ion channel blockage on neuronal excitability in stochastic HH neurons.Their results showed that very small amounts of TTX lead to a decrease in action potentials and irregular peak activity.In contrast,small amounts of TEA increased the amount and regularity of peak activity.In addition to affecting neuronal excitability by reducing the number of open ion channels,toxins can also affect membrane potential by causing a decrease in conductance(Goldwyn et al.,2011; Ma et al.,2011; Liu et al.,2013;Xu et al.,2018,2019).In the past,when poisoning was considered in a neuronal network,the neurons in it were generally considered to be uniformly poisoned.In other words,all neuronal ion channels in the network were poisoned simultaneously and to the same extent.However,due to the variability of single neurons and the fact that neural tissue is generally anisotropic,toxins might cause localized poisoning at different locations,i.e.,the poisoning was non-uniform.Neural networks with random channel poisoning have a richer dynamical behavior than those with uniform channel poisoning (Wu et al.,2013a).Moreover,the stochastic nature of ion channel gating may lead both to threshold fluctuations in neurons and also be a major source of ion channel noise generation (White et al.,2000; Maisel and Lindenberg,2020; Ding and Jia,2021).

In previous studies,although ISR induced by ion channel noise in HH neurons has been considered(Uzuntarla et al.,2013),to our knowledge the effects of potassium channel blockage on ISR have not received much attention.Therefore,some interesting questions arise: How does potassium channel blockage affect the ISR in neurons? Does the ISR in a network change when drugs block neurons in the network unevenly? How do interactions between neurons affect the ISR?

In this paper we investigate the effects of potassium ion channel blockage as well as external bias currents on the ISR of single HH neurons and explore the ISR effects in small-world networks.The HH neuron model and neural network containing ion channel blockage are introduced,and ISR effects in single neurons and neuronal networks are discussed.

2 Models and methods

The kinetic equation for the change in membrane potential over timetin HH neurons containing blocked ion channels is as follows (Hodgkin and Huxley,1952b):

whereVis the membrane potential of the neuron andC=1 µF/cm2is the membrane capacitance.GK=36 mS/cm2,GNa=120 mS/cm2,andGL=0.3 mS/cm2indicate the maximum conductance of potassium,sodium,and leakage currents,respectively.xKindicates the ratio of nonblocking potassium channels to total potassium channels,andxNais the ratio of non-blocking sodium channels to total sodium channels.Thus,ion channel blockage ratiosxKandxNaare negatively correlated with the degree of blockage.At resting potential,the cell membrane is much more permeable to potassium ions than to sodium ions,so blockage of sodium channels has little effect on the resting potential of neurons (Schmid et al.,2004; Lu et al.,2017; Xu et al.,2018; Liu et al.,2019).In the present study,we focus on the effect of potassium channel blockage and the sodium channel blockage ratio is fixed asxNa=1.0.The parametersEK=-77 mV,ENa=50 mV,andEL=-54.4 mV are the reversal potentials for potassium,sodium,and leakage currents,respectively.In addition,Iextis the external bias current that can modulate neuronal excitability.

In Eq (1),nis the activation gating variable of the potassium ion channel,andmandhrepresent the activation and deactivation gating variables for sodium channels in neurons,respectively.Considering ion channel noise in the dynamical behavior of neurons,the Fox algorithm is used (Fox,1997),where the gating variables obey the following Langevin equation:

whereαyandβyare voltage-dependent rate functions of the gating variabley(y=n,m,h) described as follows:

and the random variableξy(t) is an independent zeromean Gaussian white noise whose autocorrelation function satisfies the following equations:

In Eq (4),the total numbers of potassium and sodium ion channels in a membrane patch are given byNK=ρK×SandNNa=ρNa×S,respectively,whereSindicates the membrane area.Assuming homogeneous density of ion channels,the potassium and sodium ion channel densities areρK=18 μm-2andρNa=60 μm-2,respectively.From a statistical physics point of view,the intensity of ion channel noiseξ(t) decreases with increasingS.Throughout the study,the membrane areaSwill be used as the control parameter for channel noise.

In neuronal networks,the kinetic equations of the network are as follows:

and the autocorrelation function for Gaussian white noise in the network is as follows:

In Eq (5),Isyniindicates the synaptic current of neuroni.The connections between neurons in the network are electrical synapses,where the synaptic current of neuroniis given by

wheregeis the strength of the electrical coupling between interconnected neurons.If neuronsiandjare connected,εi，jequals 1,otherwise it is zero.The neuronal network is modeled as a small-world network (Watts and Strogatz,1998; Uzun et al.,2017; Yu et al.,2022c),which has the following network topology parameters: the degreeK=4 and the rewiring probabilityp=0.4.The topology of the small-world network does not change unless otherwise indicated.

In neuronal systems,ion channels in the area of the neuronal membrane can be blocked by certain drugs(Narahashi and Moore,1968; Hoyt and Strieb,1971).In most cases,the blockage of neuronal networks by drugs is non-uniform,so it is of significance to study the overall effect of ion channel blockage in a portion of the neuron in the network (Wu et al.,2013a,2013b).We introduce the network blockage ratio (NBR),which represents the proportion of neurons in the network with the potassium channel blockage to the total of all neurons in the network.To simplify the study process,for blocked neurons we set the top portion of neurons,e.g.,NBR=0.2,as the first 20 neurons with potassium channel blockage (100 neurons in network).We found this network setting to be adequate for our purposes,as neurons randomly set to potassium ion blockage showed the same qualitative features as in the study here.

To investigate the ISR phenomenon in single neurons,we introduced the average firing rate of the single neurons.First,the initial conditions for the neuron were chosen randomly and uniformly in the state space (V,n,m,h),where the membrane potentialsVranged from -80 mV to 40 mV and each gating variable ofn,m,andhranged from 0 to 1.Then,after an initialization time ofT0=1 s,the number of spikes occurring in the neuron duringT=10 s was recorded.Each spike is defined by a transmembrane potential above -20 mV.Therefore,the average firing rate of the neuron is calculated by

whereH=100 indicates the number of times the process is repeated.This is enough repetitions for the firing rate to satisfy the statistical law.In addition,the average firing rate of the network can be calculated using the following equation:

and the number of nodes in the network is fixed atN=100.In the study of the numerical integration of this system,the fourth-order Runge-Kutta method is used with a step size of 10 μs.

3 Results

3.1 ISR in single neurons with ion channel noise

The effect of different ion channel noise and potassium channel blockage on the neuronal membrane potential is shown in Fig.1.Looking at the left and right columns it can be seen that there is a continuous change in the membrane potential of the neuron as the membrane area increases,i.e.,firing state→resting state→firing state.However,the firing of the neurons in the middle column barely changed.A horizontal comparison shows that the firing of neurons is only likely to be inhibited at moderate intensities of noise.The results show that neuronal firing is inhibited at moderate intensities of noise when potassium channel blockage is strong or weak,which indicates that the neuron undergoes ISR.However,in the case of moderate potassium channel blockage,neuronal firing was barely affected by the noise.

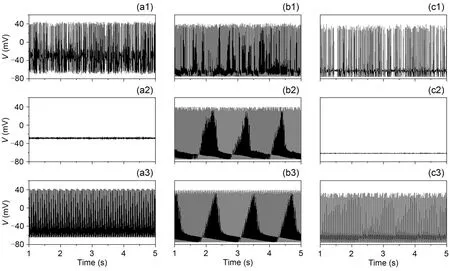
Fig.1 Time evolution of membrane potential under conditions of different noise intensities and potassium channel blockage (Iext=4.0 μA/cm2): (a1) xK=0.10,S=1×102 μm2; (a2) xK=0.10,S=1×104 μm2; (a3) xK=0.10,S=1×106 μm2; (b1) xK=0.50,S=1×102 μm2; (b2) xK=0.50,S=1×104 μm2; (b3) xK=0.50,S=1×106 μm2; (c1) xK=0.88,S=1×102 μm2; (c2) xK=0.88,S=1×104 μm2; (c3) xK=0.88,S=1×106 μm2

To investigate the effect of potassium ion blockage on neuronal firing activity,the neuronal average firing rateris plotted against the membrane areaSfor differentxKin Fig.2.The observations show that for different values ofxK,different changes in the firing rate of neurons occurred.Notably,atxK=0.09 the neuronal firing activity is diminished with decreasing noise intensity and even becomes resting.AtxK=0.20,xK=0.30,andxK=0.40,there is no apparent minimum in firing rate.The ISR is only observed for some specific values ofxK.To comprehensively understand the effect ofxKon the ISR effect,a contour plot ofrin theS-xKplane is shown in Fig.3.The external bias current is fixedIext=4.0 μA/cm2,and the blue areas indicater=0.The results show that for 0.11＜xK＜0.83,rgradually decreases,and then remains unchanged in its natural firing state.When 0.10＜xK＜0.11 and 0.83＜xK＜0.91,rdecreases and then increases with decreasing noise intensity (increasing membrane area),i.e.,the ISR effect occurs.AtxK＞0.91 andxK＜0.10,the neuron gradually changes to a resting state.In other words,the ISR occurs only for a certain small range of potassium channel blockage ratios.Additionally,when the membrane area is small,the relationship betweenxKandris inverse.This means that potassium channel blockage promotes neuronal firing behaviour at appropriate noise levels.This is similar to previous results (Zhou et al.,2020).

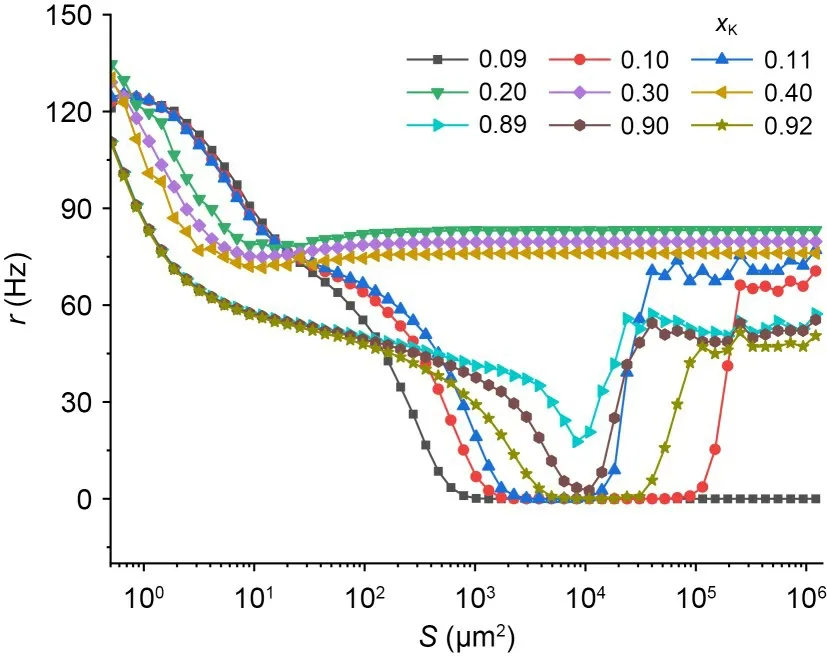
Fig.2 Occurrence of ISR in HH neurons with different potassium channel blockages: average firing rate of neurons versus noise intensity for different potassium channel blockage conditions

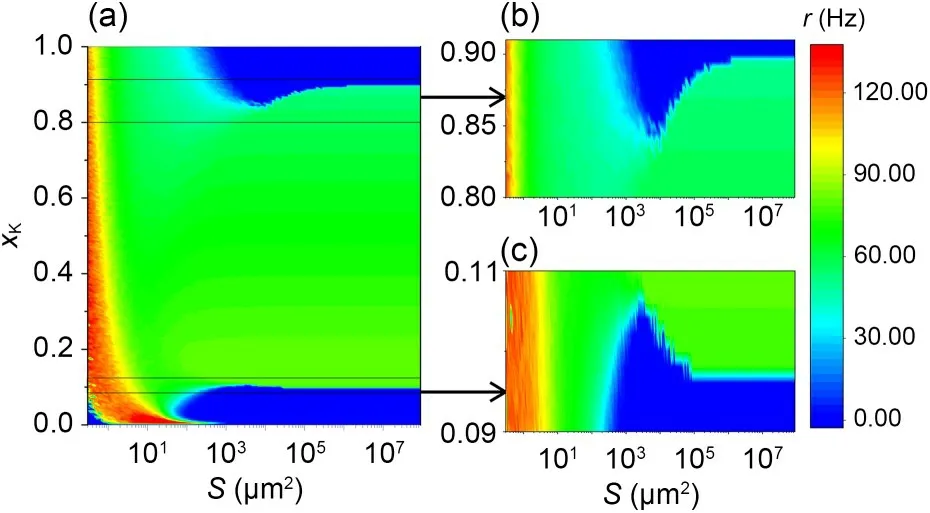
Fig.3 Dependence of neuronal firing rate on noise intensity and potassium channel blockage (a) (Iext=4.0 μA/cm2).(b) and(c) are enlargements of the small areas in the diagram in(a).Reference to color refers to the online version of this figure

The above neuronal responses to different degrees of potassium channel blockage can be interpreted in terms of the bifurcation diagram in Fig.4,which is the asymptotic behavior of the voltage of noise-free neurons against the potassium channel blockage ratioxK.ForxK＜x1andxK＞x4,the only attractor is the stable fixed point (SFP),which means that the neurons gradually change to the resting state with decreasing noise intensity.AtxK=x1andxK=x4,the saddle-node bifurcation produces stable and unstable limit cycles (SLC and ULC).The stable limit cycles correspond to the spiking behaviour.The ULC is the boundary between the steady-state SFP and the SLC.In the bistable state,xKhas little effect on SFP and SLC,but changes the size of the ULC.The ULC converges asxKincreases forxK∈(x1,x2) and asxKdecreases forxK∈(x3,x4),implying a decrease in the SFP attractor basin.This means that the neurons have difficulty transitioning from SLC to SFP,and ISR is less likely to occur.Note that SFP does not exist whenxK∈(x2,x3),so the neuron cannot transition from the limit cycle to the non-peak state and cannot undergo ISR effects.In conclusion,ISR occurs in the bistable region corresponding toxK,which is consistent with previous investigation (Uzuntarla et al.,2013).

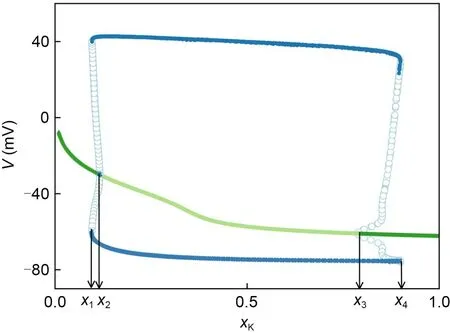
Fig.4 Bifurcation plot of the Hodgkin-Huxley neuron model versus the ratio of potassium channel blockage xK (from 0 to 1.0).The four critical points x1,x2,x3,and x4 are the four bifurcation points.Dark (light) green indicates stable(unstable) equilibrium,and blue solid (open) circles indicate asymptotic minima and maxima of voltage during stable(unstable) spiking behavior.Regions (x1,x2) and (x3,x4) are bistable regions.The parameter is fixed at Iext=4.0 μA/cm2.Reference to color refers to the online version of this figure

The variation of the four critical points in the HH neuron model with external bias current is shown in Table 1.AsIextincreases,x1andx2change slightly,whilex3andx4increase significantly.The results in Table 1 indicate that the external bias current can change the interval of the bistable state.

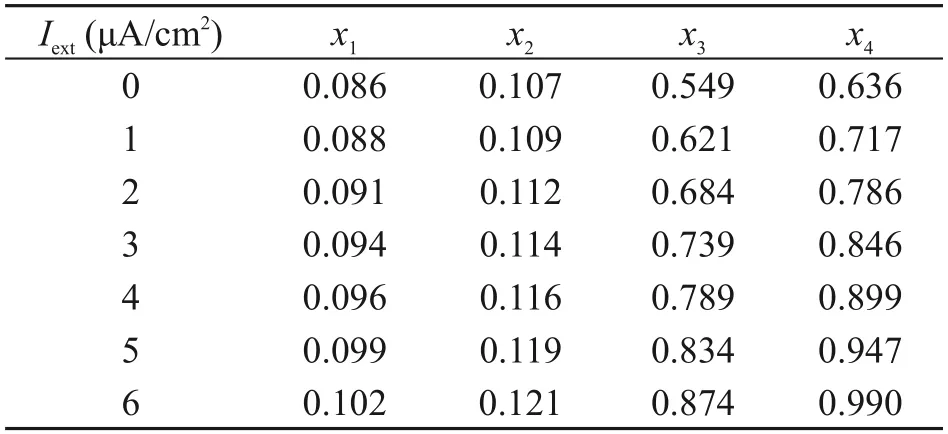
Table 1 Statistics of the four critical points at different external bias currents (Fig.4)

To explore the effect of an external bias current on ISR,Fig.5 shows the variation of neuron firing rate with noise intensity for different external bias currents.AtIext=1.0 μA/cm2andIext=5.5 μA/cm2,no ISR effect occurs in the neurons.The results indicate that the external bias current changes the interval of membrane area corresponding to a neuron with a firing rate of 0.Furthermore,Fig.6 shows contour plots of the variation of firing rate with membrane area and external current for three different potassium ion channel blockages.Fig.6a shows that forxK=0.10,ISR effects occur in the range ofIext∈(1.5,5.5) μA/cm2,and an increase in external current promotes ISR effects.ForxK=0.40,the neuron does not undergo ISR effects (Fig.6b).ForxK=0.90,the external current for ISR to occur is larger,at approximatelyIext∈(4.5,5.5) μA/cm2,and an increase in external current suppresses ISR effects (Fig.6c).Table 1 shows that asIextincreases,the morex2is greater than 0.10.As a result,whenxK=0.10,the SFP attractor basin grows as the current does,so an increase in external current promotes the ISR phenomenon and,vice versa,x3approaches 0.90 asIextrises,implying that atxK=0.90,an increase in current causes the SFP attractor basin to shrink,which in turn suppresses the ISR.

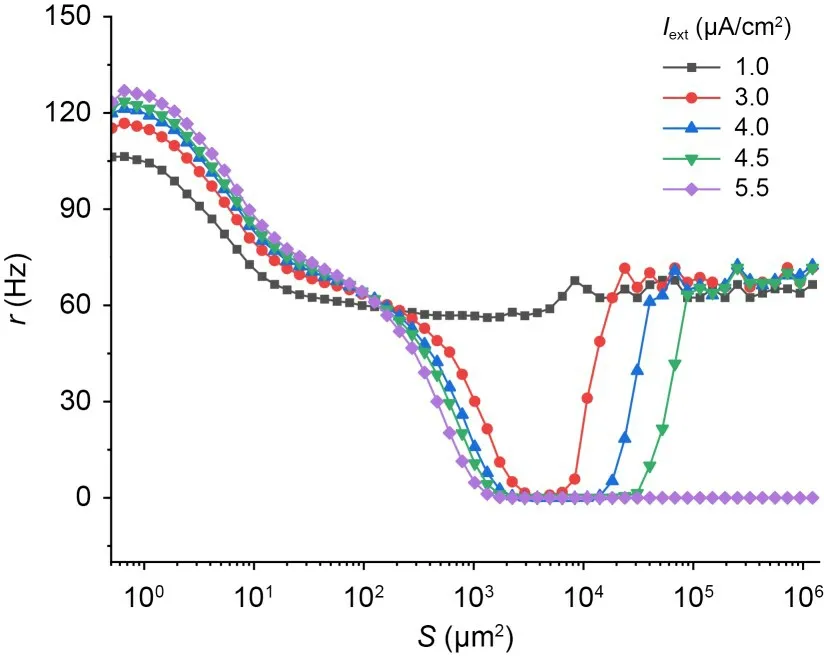
Fig.5 Mean firing rates of neurons versus noise intensity under different external bias current conditions.The other parameter is set to xK=0.1

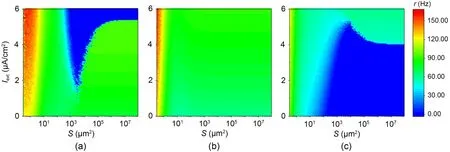
Fig.6 Contour plots of the average firing rate r in the Iext-S plane at different potassium channel blockage ratios xK: (a) xK=0.10; (b) xK=0.40; (c) xK=0.90.Note that xK is negatively correlated with the degree of blockage

3.2 Inverse stochastic resonance of small-world neuronal networks

ISR in isolated neuronal networks (i.e.,where there are no synaptic currents between neurons) is first discussed.Since the neuronal network is non-uniform in its response to drugs,we use NBR to denote the proportion of neurons in the network with blocked potassium channels to the total number of neurons in the network.To simplify the study process for blocked neurons,we set the top portion of neurons,e.g.,NBR=0.2,to the first 20 neurons with potassium channel blockage.ThexKof this part of the neuron is fixed at 0.1 (within the bistable interval).In the following,when calculating the firing rate of the network,each neuron in the network is chosen with the initial values fixed at (-30.08,0.65,0.44,0.44) in the state space (V,m,n,h).Fig.7a plots the average firing rate of networkRversus membrane area for no coupling currents between neurons,for different network blockage ratios NBR.The results indicate that the firing first decreases and then increases with increasing membrane area for different NBRs.TheRis zero at moderate intensity of noise.This means that in the isolated neural networks,the ISR phenomenon occurs for different NBRs.In the case of relatively high noise intensity,all neurons in the network are firing,the NBR increases,and the firing rate increases.Figs.7b and 7c show the firing distribution and spatio-temporal plots,respectively for the network blockage ratios of 60% under small noise.It can be seen that the first 60% of neurons are in a discharging state and the last 40% are in a resting state.Therefore,only bistable neurons in the network are firing at low noise intensities,and the firing rate of the network is positively correlated with the network blockage ratios.

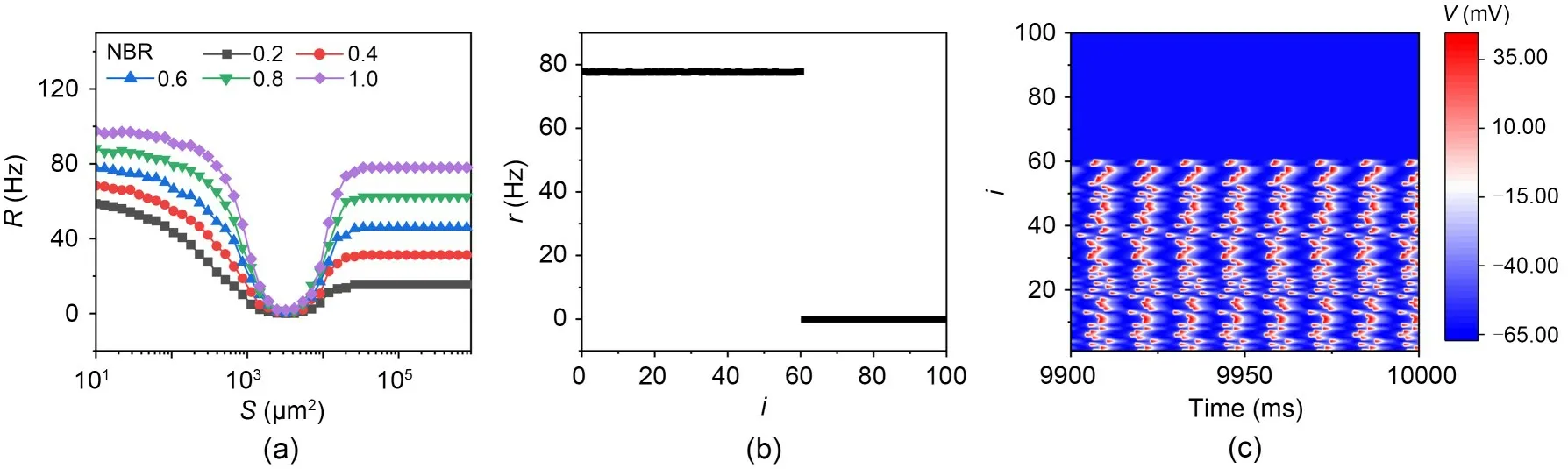
Fig.7 ISR in isolated neuronal networks: (a) average firing rate of the network as the function of membrane area for different NBRs,with coupling strength ge=0 mS/cm2; (b) firing rate of each node in the network under small noise,NBR=0.6 and S=1×105 μm2; (c) spatio-temporal plot in the isolated network under small noise,NBR=0.6 and S=1×105 μm2

We then explored ISR in the small world network with different electrical coupling strengthsge.Overall,the ISR is a robust phenomenon across different electrically coupled small-world networks.In Fig.8a,the ISR was clearly observed under different NBRs.In addition,the membrane area threshold (i.e.,the membrane area when the firing rate of the network starts to jump from zero) is different for different NBRs.Fig.9 shows the threshold versus the NBR in the case wherege=0.04 mS/cm2.The results show that the threshold decreases as NBR increases.This means that the range of noise that can inhibit neuronal firing activity is progressively reduced as the NBRincreases.In other words,the increase in the network blockage ratios at small coupling strengths suppresses the ISR effect.

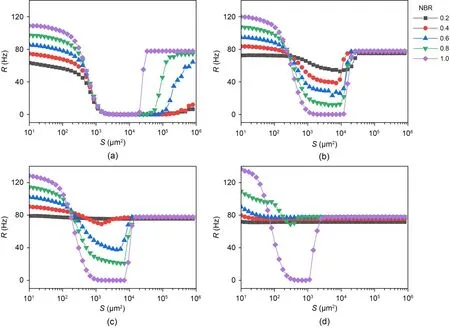
Fig.8 ISR emergence in the small world network of electrically coupled neurons at different coupling strengths.The average firing rate is the function of membrane area for different coupling strengths ge: (a) ge=0.04 mS/cm2; (b) ge=0.10 mS/cm2;(c) ge=0.17 mS/cm2; (d) ge=0.60 mS/cm2

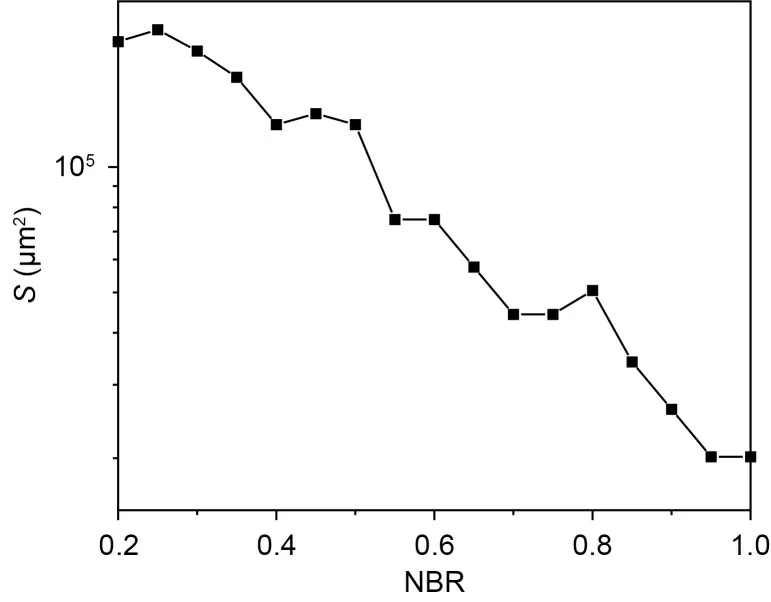
Fig.9 Relationship between the threshold of membrane area and the network blockage ratio.The threshold refers to the membrane area corresponding to the jump of R from zero,with ge=0.04 mS/cm2

Comparing the right side of Fig.8a with the middle of Fig.8b,it can be found thatRin the former gradually increases with increasing NBR,while in the latter it changes in the opposite direction.What are the differences in their kinetic mechanisms? As shown in Fig.8b,the minimum value of theRdecreases as the network blocking ratio NBR increases,indicating that the ISR becomes more pronounced with higher NBR.To explain this phenomenon,we use the relative abundance of spiking states (NS/N) to represent the proportion of neurons in the network that is in the spiking state.The top panel in Fig.10 represents theNS/Nfor three different NBRs,and the bottom panel represents the change in the firing rate of each neuron in the corresponding state.The observation shows that the reason for the decrease inRat moderate noise is that the part of the neuron with potassium channel blockage is resting.So the larger the NBR,the smaller theRof the network under moderate noise.The firing rate of neurons is suppressed to zero due to the ‘trapping effect’ (Uzuntarla et al.,2017b).In bistable neurons,the SFP and the SLC are divided by the ULC.This boundary is closer to the SLC.Thus,for moderate noise levels,the neuron in the firing state encounters a noise kick that causes it to cross the boundary and enter the basin of the SFP where it is captured.Once captured,the neuron will gradually became resting and have difficulty in being returned to the SLC.To sum up,under moderate noise intensityRbecomes smaller because the noise suppresses the firing of bistable neurons.The more the number of bistable neurons in the network,the more pronounced the suppression of the firing rate of the network.

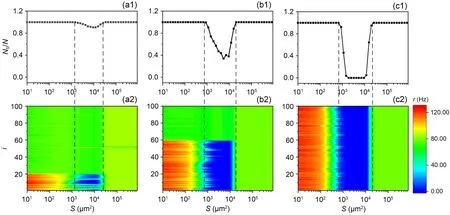
Fig.10 Firing behavior of neurons at different ratios of network blockage.ge=0.10 mS/cm2,top panel is the relative abundance NS/N of neurons in the firing state,and bottom panel is the firing rate of each neuron in the network as a function of membrane area.(a1 and a2) NBR=0.2; (b1 and b2) NBR=0.6; (c1 and c2) NBR=1.0

Fig.8c represents theRversus membrane area for different NBRs for the coupling strengthge=0.17 mS/cm2.There is no significant ISR phenomenon on the network when NBR=0.2.Comparing Fig.8b and Fig.8c,we find that for the same NBR,an increase in coupling strength results in a greater minimum value of the curve.This is because the SFP of the bistable neuron (Fig.11 green dot) is outside the excited trajectory of the monostable neuron (Fig.11 blue trajectory),such that a potential difference will form between the bistable neuron in the resting state and the monostable neuron in the firing state.When the coupling strength becomes greater,it leads to a greater synaptic current in the bistable neuron,and the neuron discharges steadily as a result.That can be confirmed in Figs.12a and 12b;when the coupling strength increases,the bistable neuron will be pulled to the limit circle in a firing state.This effect diminishes when the number of monostable firing neurons decreases.In Fig.12a,the ratio of the number of monostable to bistable neurons is 8:2,20% of all bistable neurons firing forge=0.17 mS/cm2.However,in Fig.12b2,there are some bistable neurons that remain in the resting state.There is little difference in the firing states of the neurons between Fig.12c and Fig.12d.Due to this effect,an increase in coupling strength suppresses ISR.Fig.8d indicates that significant ISR only occurs at NBR=0.8 and 1.0 for coupling strengthge=0.6 mS/cm2.Thus,as long as there is a potential difference between monostable and bistable neurons,a strong coupling current will override any effect that noise may have,given a sufficiently high coupling strength.So an increase in coupling strength will suppress ISR.

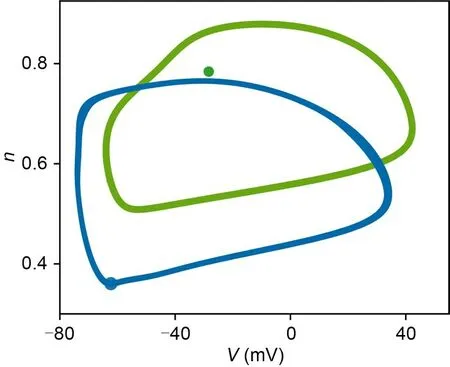
Fig.11 Phase diagrams of bistable and monostable neurons in the (V,n) plane.Green indicates SFP and SLC for the bistable neurons,and blue indicates resting state and stimulated trajectory for the monostable neurons.Iext=4.0 μA/cm2.Reference to color refers to the online version of this figure

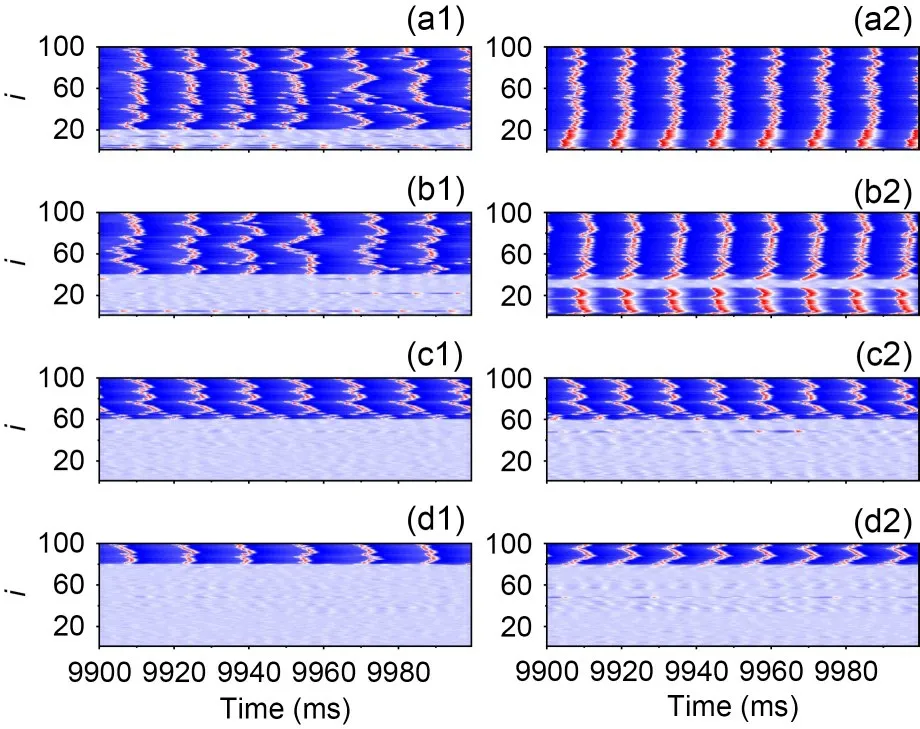
Fig.12 Behaviour of neurons in the network with different coupling strengths and network blockage ratios.S=4000 μm2,for left column ge=0.1 mS/cm2,and for right column ge=0.17 mS/cm2.(a1 and a2) NBR=0.2; (b1 and b2) NBR=0.4;(c1 and c2) NBR=0.6; (d1 and d2) NBR=0.8

In addition,the ISR phenomenon occurs regardless of the coupling strength and the firing rate is suppressed to zero when the NBR is 100%.Because each neuron in the network is a bistable neuron,there is no monostable neuron to pull a bistable neuron from the stable fixed point to the limit circle.Each neuron has the potential to undergo ISR,and firing rates of neurons are all suppressed to zero at moderate noise intensities.

The minimum firing rate of the network with respect to the NBR at different coupling strengths is shown in Fig.13.It shows that at smaller coupling strengthsge=0.04 mS/cm2,the minimum value of the network firing rate is zero regardless of the NBR.This means that ISR will occur in small coupled neuronal networks regardless of the NBR.Comparing the two curves for coupling strengths of 0.17 and 0.60 mS/cm2,it can be seen that,as the coupling strength increases,the range of NBR that can generate ISR appearances gradually decreases.For NBR=1.0,the ISR occurs,and the minimum firing rate is zero.Moreover,we also observed that the threshold for the minimum NBR that can occur with ISR increases as the coupling strength increases,because in the case of moderate noise,the noise kicks the bistable neuron from the limit cycle to the stable equilibrium,whereas a sufficiently large coupling current gives a stimulus to return it to the limit cycles.The higher the coupling current,the less the network firing rate decreases for a given network blocking ratio,so that the increasing coupling strength counteracts the trapping effect.

Fig.13 Minimum value of the average firing rate relative to the NBRs in different electrically coupled neuronal networks

To further investigate the relationship between the average firing rateRand the coupling strengthge,Fig.14 shows the response of the firing rate of the network to the coupling strength at different noise intensities.As shown in Fig.14a,for a noise intensity ofS=1000 μm2,Rfirst decreases slowly to a minimum or remains constant and then increases rapidly asgegradually increases.However,for NBR=0.2 and NBR=0.4,there is no significant minimum value.Fig.14b shows the variation of the average firing rate with coupling strength for a noise intensity ofS=3000 μm2.The observation shows that for different NBRs,the average firing rate of the network increases rapidly from zero as the coupling strength increases.In addition,the threshold of the coupling strength for this shift increases as the NBR increases.In both plots in Fig.14,the curves have a rapid rise and then fall in common.We explored the reasons for this phenomenon.

Fig.14 Average firing rate of the network with coupling strength for moderate noise intensity: (a) S=1000 μm2; (b) S=3000 μm2

Two conditions are required for a bistable neuron to fire under moderate intensity noise: a sufficiently large coupling strength and a potential difference between it and the monostable neurons.Therefore,for the network’s firing rate increasing from zero,we analyzed and reasonably speculated that the network’s firing rate first increased because the monostable neurons were first in the firing state.Afterwards there would be a potential difference between the monostable and bistable neurons,due to the increase in coupling strength,for the bistable neurons to be pulled into the firing state.Fig.15 confirms our speculation.We take Fig.14a(NBR=0.6) as an example,Fig.15 shows the distribution of firing at three coupling strengths during the period of increasing network firing rate.It can be seen that first the monostable neurons fire,then the number of bistable neurons in the firing state gradually increases with increasing coupling strength.

Fig.15 Effect of coupling strength on the firing rate of neurons in small-world networks on moderate noise intensity (S=1000 μm2,NBR=0.6): (a) ge=0.08 mS/cm2; (b) ge=0.20 mS/cm2; (c) ge=0.30 mS/cm2

It is worth noting that in Fig.14,except for NBR=1.0,the firing rate of the network reaches a maximum and then gradually decreases.Taking Fig.14b as an example,the NBRs are 0.2 and 1.0,and the spatio-temporal plot and firing distribution at large coupling strengthge=1.0 mS/cm2are shown in Fig.16.We know that the firing rate of neurons with NBR=1.0 is greater than that of neurons with NBR=0.2 firing rate.This is because,at large coupling strengths,the neuronal networks are all in a discharge-synchronous state and the firing rates are all close to the natural firing rates.However,on the one hand,there is heterogeneity between bistable and monostable neurons in which the eigenfrequencies of the two are not the same while,on the other hand,electrical coupling is connecting neurons throughout the discharge process and thus the membrane potential difference that always exists between neurons will coordinate the discharge frequencies with each other.So the overall firing rate of the network is smaller than the natural discharge rate,and the more bistable neurons there are,the larger is the network discharge rate.

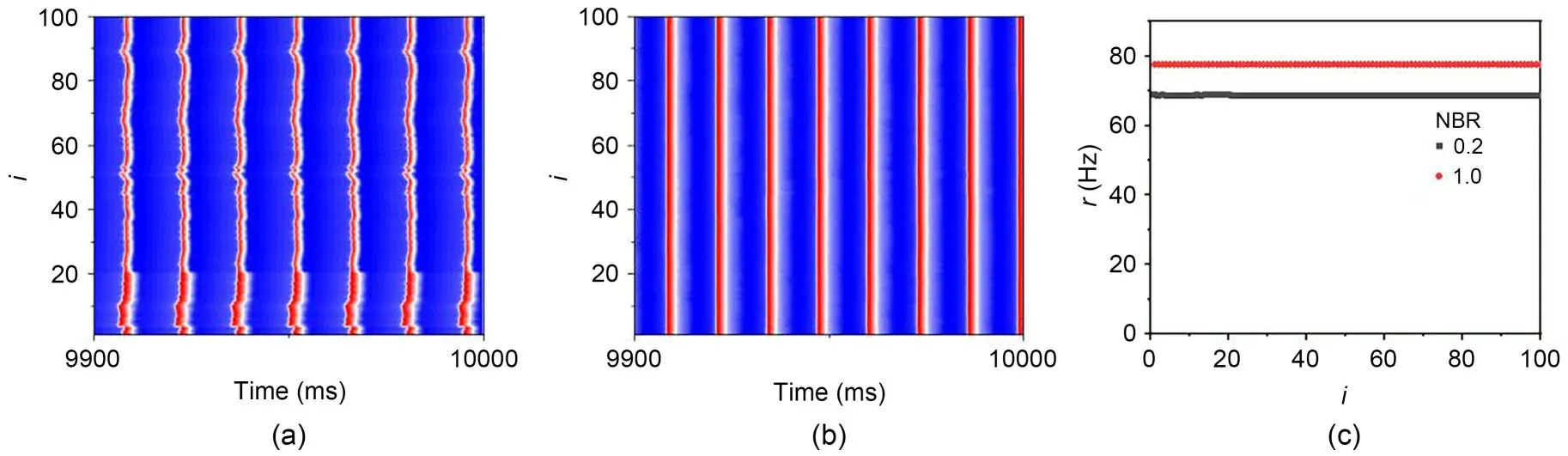
Fig.16 Effect of network blocking ratio on neuronal firing in small-world networks on moderate noise intensity.Spatiotemporal plots for two different network blockage ratios of NBR=0.2 (a) and NBR=1.0 (b) with ge=1.0 mS/cm2 and S=3000 μm2; (c) is the firing distribution corresponding to (a) and (b)

4 Conclusions

Previous studies have shown that the ISR induced by a variety of factors is widespread in single neurons and neuronal networks (Uzuntarla,2013; Uzuntarla et al.,2013,2017b).Certain drugs can affect neuronal information transfer processes by causing ion channel inactivation (Narahashi and Moore,1968; Hoyt and Strieb,1971).Currently,the effect of potassium channel blockage on ISR in HH neural systems has not received much attention.

In this paper,we focused on the effect of potassium ion channel blockage on ISR in HH neural systems.The results show that in single neurons,ion channel noise-induced ISR effects can occur only at a certain small range of potassium channel blockage ratios.The bifurcation analysis showed that within this small range is the bistable region,where stable fixed point and stable limit cycles coexist,and this range is regulated by the external bias current.Therefore,the bistable kinetic structure of HH neurons and external noise are necessary for the generation of ISR.

We further investigated the ISR effect in smallworld networks.Since drug effects are non-uniform across neurons in the network,we introduced the network blockage ratio NBR,which is the ratio of neurons with potassium channel blockage in the network to the total neurons in the network.At small coupling strengths,an increase in NBR resulted in shorter ISR durations.When the coupling strength is increased,the ISR was more pronounced in the case of large NBR.The reason for the presence of ISR is that the firing of bistable neurons is inhibited at moderate levels of noise.However,when there is a potential difference between the bistable and monostable neurons and the coupling strength is increased,this inhibition is counteracted.In summary,the appearance of ISR depends on the interaction of the network blockage ratios,the coupling strength,and the ion channel noise.

Previous studies have shown that ISR has been observed in individual Purkinje cells of the rat brain(Buchin et al.,2016),suggesting that the necessary kinetic structures for ISR to occur are present in biological individuals.Thus,ISR can be used to improve biological function.For example,the transmission of locally optimal information during cerebellar information processing (Buchin et al.,2016),the suppression of specific bands in working memory (Dipoppa and Gutkin,2013),and the stochastic facilitation effect in auditory brain stem cells (Schmerl and McDonnell,2013).In addition,ISR can be used to filter irrelevant information,thus allowing the nervous system to process information more selectively.In this paper,we have only considered ISR in small-world networks with electrically coupled connections.However,the phenomenon of ISR in more realistic neuronal (Ma et al.,2019) network structures as well as in connection patterns remains to be explored.Examples include neural networks in the cerebral cortex that are connected by the balance of excitatory and inhibitory synapses (Shu et al.,2003; Heiss et al.,2008).

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No.12175080) and the Fundamental Research Funds for the Central Universities (No.CCNU22JC009),China.

Author contributions

Xueqing WANG and Dong YU designed the research.Xueqing WANG and Dong YU processed the corresponding data.Xueqing WANG wrote the first draft of the manuscript.Yong WU,Tianyu LI,and Qianming DING helped to organize the manuscript.Dong YU and Ya JIA revised and edited the final version.

Conflict of interest

Xueqing WANG,Dong YU,Yong WU,Qianming DING,Tianyu LI,and Ya JIA declare that they have no conflict of interest.