用于激波增强的变截面激波管设计

白世杰，梁兴雨，王 昆

用于激波增强的变截面激波管设计

白世杰，梁兴雨，王 昆

(天津大学内燃机燃烧学国家重点实验室，天津 300350)

相对于常规等截面激波管，相同长度管道条件下，变截面的设计可显著增强入射激波的强度．考察了变截面收缩曲面对激波管内部气体流动特性的影响，进而设计该类新型激波管．基于理想不可压缩一维流动、可压缩流动、经验公式和经验公式加等4种理论方法，建立了不同的变截面收缩曲面替换段的二维几何模型．以上理论模型结合有限元分析，开展数值模拟研究，获取了亚音速和超音速工况下压力分布等值线云图，进而分析了不同长度收缩曲面的影响．结果表明：相对于其他3类理论方法，基于经验公式加R设计的收缩曲面更适用于变截面激波管的设计．

变截面激波管；收缩曲面；可压缩流；有限元分析；压力等值线

燃烧不仅为我国提供了超过90%的一次能源供应，同时也是航空航天的主要动力源[1-2]．在实现碳达峰和碳中和目标的背景下，碳氢燃料燃烧作为我国主要CO2排放源成为当前社会关注的焦点[3-4]．其中碳氢化合物的燃烧是大气污染物和温室气体CO2的主要排放源之一[5]．为了利用先进燃烧技术达到近零排放，需要建立其化学反应动力学模型来模拟各种碳氢燃料的燃烧过程[6-7]．激波管是发展和验证燃烧化学反应动力学模型的主要工具之一，不仅可以进行点火延迟研究，也可以对热解和氧化反应产物的种类进行高精度的定量分析[8]．随着对激波管实验压力5需求的升高，对其驱动段承压、密封等技术的要求可能会导致过高的加工成本，同时也可能超出现有的技术极限[9]．在激波管驱动段具备同等技术条件下，采用变截面设计是显著增加实验压力的有效方法之一[10].

激波管的变截面设计通常基于激波动力学理论和气体动力学理论进行计算[11]．基于激波动力学理论[12-13]的计算常用于将平面激波转换为圆柱激波，然后对激波的R-M(Richtmyer-Meshkov)不稳定性开展研究[14]．而在接近圆柱激波的中心点时，从理论上来讲激波强度可以无限制增加．如果控制其增加强度使其达到实验所需的要求，然后再将其转化为平面激波，就实现了在不改变波形的情况下增强了平面激波的强度．因此，Zhan等[15]通过激波动力学理论得到了形状为凹-平-凸的收缩曲线，然后通过纹影实验和数值模拟验证了其模型的准确性．基于气体动力学理论的计算多用于研究变截面激波管内部的气体流动特性．对于低密度气体或者对激波强度要求不高而对波形要求较高的情况，为了节省驱动气体的用量常采用扩张激波管；而为了获得更高强度的激波，经常采用驱动段截面大于被驱动段的收缩激波管．俞鸿儒等[7]通过对扩张激波管内气体在不同马赫数下流动特性的研究，提出了扩张激波管存在4种不同的流动区域，认为在实际的计算过程中需根据其流动特性选用不同的理论推导．林健民等[16]通过对比变截面激波管和插入多孔板的等截面激波管在不同驱动比下入射激波强度的变化，实现了在较高的驱动比下获得低强度入射激波，用于激波管在低压条件下开展小量程压力传感器的动态性能校准．

自20世纪90年代以来，激波管反应器的种类逐渐丰富，其中最具有代表性的激波管包括斯坦福大学传统激波管[17]、伊利诺伊大学芝加哥分校UIC单脉冲激波管[18]和阿贡国家实验室[19]无膜激波管等．目前只有UIC单脉冲激波管采用变截面方式提升实验压力5，然而其仅采用了较为粗糙的直线收缩方式作为变截面联接段，而不是顺滑的曲面收缩方式．曲面的设计可以优化其内部的气体流动和激波运行．

传统等截面激波管的压力计算方法较为完善．对于变截面激波管，当前基于激波动力学理论的优化计算只关注其激波波形的变化，未考虑其内部气体流动特性的变化；基于气体动力学理论/方法缺乏对激波管收缩曲面的基础研究．因此，本文基于理想不可压缩一维流动、可压缩流动、经验公式和经验公式加等4种理论方法，设计了4类收缩曲面，建立了各自所对应的二维几何模型，然后结合有限元分析开展了数值模拟研究，最后对比分析了不同模型的气体压力等值线分布．

1 数值分析

本文选取了4种变截面收缩曲面设计方法进行了详细的计算，其中包括不可压缩流动、经验公式以及对经验公式的优化、可压缩流动.

1.1 不可压缩流动

理想不可压缩流体一维流动假定每个截面上的气流参数是均匀的，通过给定轴向加速度分布，然后计算其收缩曲面．假设进口截面的面积和速度为1和1，出口截面面积和速度为2和2，收缩曲面长度为．根据一维流动动量守恒定律，可得：

在收缩段入口处和出口处流体都是处于稳定状态，其加速度为0，即＝0和＝时，＝0．假设轴向加速度为正弦分布，即：

式中：为加速度系数，m/s2；其值取决于气流经过收缩曲面的速度平方增量．

由式(1)和式(2)可得：

从＝0到任意处对式(3)积分，即：

化简得：

当＝时，＝2，由式(5)可得：

把式(1)、(6)代入式(5)可得任意处的截面积为

根据式(7)可确定任意位置处收缩曲面的横截面积，然后将其转换为半径即获得其收缩曲面．

1.2 经验公式

收缩曲面计算的经验公式根据理想轴对称流动推导得出：

式中：out为出口半径；in为入口半径．

1.3 经验公式加R的优化

当变截面前后管径收缩比大于6时，收缩曲面在前半部分会急剧收缩，而后半段基本不再收缩．这就会导致气流剧烈收缩，从而破坏气流的均匀性．解决这一问题的方法就是选取一个合理的1(式9)得到一个新的半径再减去1即为所求的收缩曲面．

1.4 可压缩流动

考虑气流压缩性建立了收缩曲面和马赫数之间的关系可得：

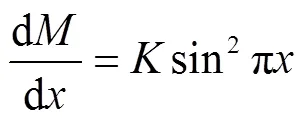
其余推导过程同不可压缩流一致，可得式(11)，根据马赫数和截面积的关系就可以得到收缩曲面．

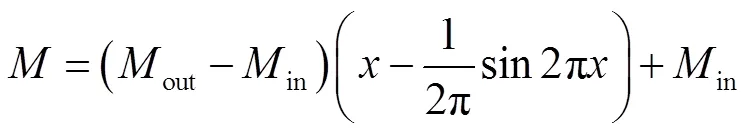
式中：in为变截面前马赫数；out为变截面后马赫数.

以上4种方式均基于理想流动方程，且假定入口端气流完全均匀，而实际上这两个假定可能难以完全满足．通常应先根据理论公式计算获得理论收缩曲面，然后据此制作模型开展实验验证或适当修正，进而确定最终实际可用的收缩曲面．

2 数值模拟

2.1 初始参数

激波管内径大小影响气流边界层，但当其管内径大于100mm时，其边界层效应基本可以忽略[6]．因此，本研究选取激波管驱动段的最小内径为105mm，同时收缩比通常在4～5之间，故激波管被驱动段的内径为210mm．收缩段的长度一般采用入口端内径的0.5～1.0倍，因此初步选定收缩段长度为1000mm．

2.2 收缩曲面

图1为基于以上理论计算得到的收缩曲面．从图中可以看出，基于不可压缩流获得的收缩曲面比基于其他方式获得的收缩曲面更陡峭；而基于可压缩流得到的收缩曲面在前半段最为平缓；基于经验公式加得到的收缩曲面在后半段最为平缓．相比经验公式加确定的收缩曲面，基于经验公式的收缩曲面在前半部分更加平缓，从而减缓前期剧烈收缩导致气流均匀性差的现象．

图1 基于不同理论方法计算的收缩曲面

2.3 曲面方程拟合无关性分析

基于每一种理论方法可以确定激波管任意位置所对应的内径，通过选取多个位置内径数据点的拟合确定收缩曲面方程(进而提供给数控机床加工)．显然选取点的数量可能对拟合曲面产生较大影响，本文首先对其开展无关性分析．基于不可压缩流公式，图2分别选取了10个、20个、40个、50个和100个数据点拟合得到收缩曲面．由图2可见，各拟合曲面趋势基本一致，但从其放大图中可看出，在收缩曲面前端随着取点数量的增加逐渐平滑．当取点数量大于40时，收缩曲面的变化则差别不大．基于以上分析，本文选取50个数据点拟合收缩曲面方程.

图2 收缩曲面方程拟合取点数量的无关性分析

2.4 二维几何模型

基于不同理论，图3建立了二维几何模型示意图．模型包含驱动段、被驱动段、替换段和实验段，依据替换段的截面特点将其分为普通激波管和变截面激波管．驱动段和被驱动段间由隔膜分隔，以便于两端填充不同气体．基于不同理论计算的收缩曲面作为替换段内壁面，建立其二维几何模型．其中，等截面和直线变截面激波管作为参照组，直线变截面激波管的替换段直线斜度由驱动段内径、实验段内径和替换段长度共同决定．等截面激波管的实验段内径为210mm，变截面激波管的实验段内径为105mm，模型4部分长度均为1000mm．

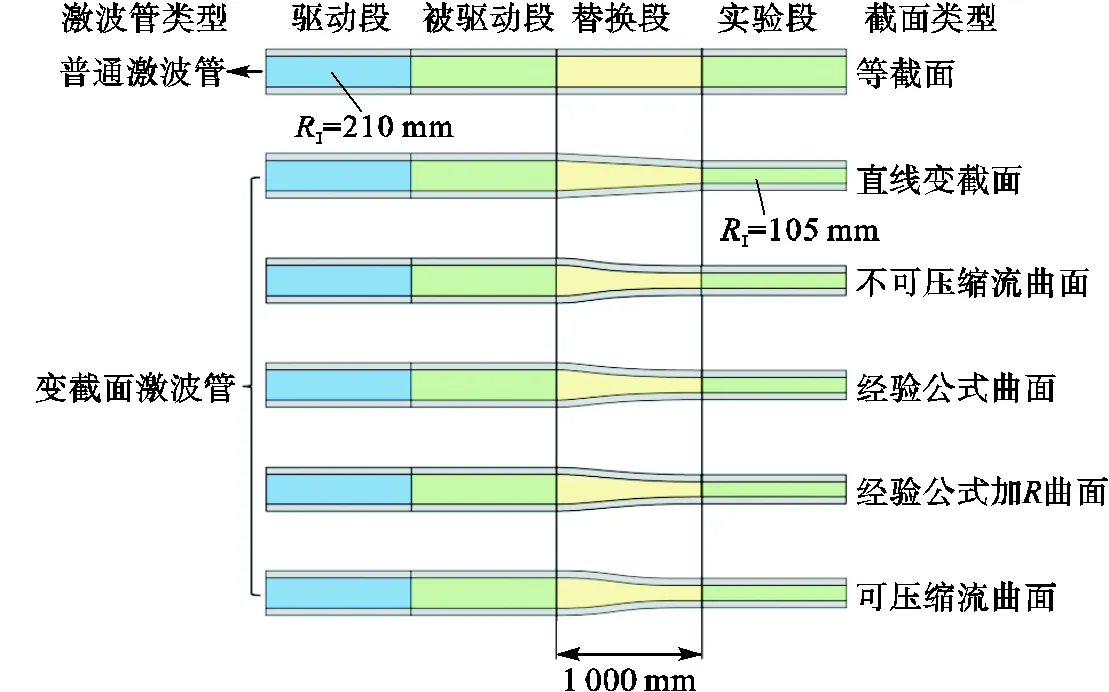
图3 不同界面类型二维几何模型示意

2.5 边界条件

在有限元分析中定义二维几何模型各部分材料属性和边界条件．进行模型验证时驱动段内部选取氦气，其余3部分内部选取空气．为避免不同气体混合扩散增加模拟研究的不确定性，在模拟仿真过程中四部分内部均为氦气，管道材料为304不锈钢．管道内部为压力声学瞬态场，以观察不同收缩曲面对其内部气体流动压力分布的影响，管道内部初始参数设定如表1所示．管道自身为固体力学场，其位移和速度场均设为0．

表1 初始参数设定

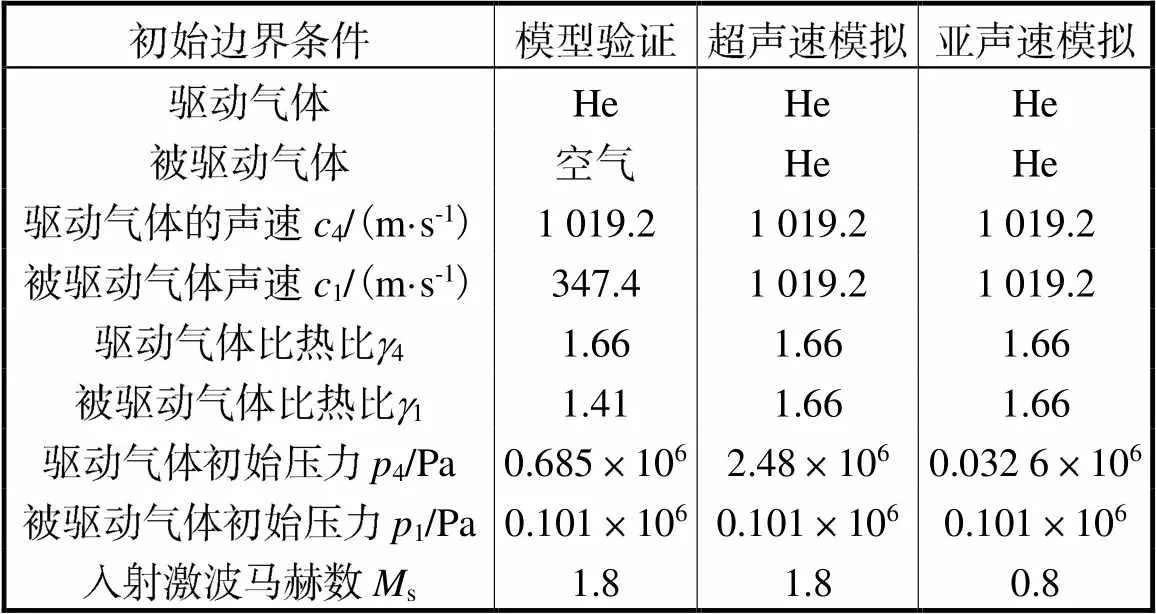
Tab.1 Initial parameter settings

2.6 模型验证

根据等截面激波管理论计算得：

通过对比等截面激波管模型和理论计算各自对应的5验证模型准确性．应用表1中用于模型验证的初始边界条件，计算两个5的相对误差，确定模型精度是否满足设计需求，理论计算值5为1.06×106Pa，有限元模拟值5为1.02×106Pa．两者的相对误差为4%；而通常相对误差小于5%则其精度满足设计需求．需要注意的是，为了减少不确定因素对数值模拟产生影响，本文中其他的数值模拟驱动和被驱动气体均设定为同种气体(氦气He)．

3 结果和讨论

3.1 超音速条件下变截面对压力分布的影响

通过有限元数值模拟可得激波管的表面声压图和压力等值线图，后期对替换段放大处理，便于观察其内部压力分布的变化规律．表面声压的颜色会覆盖压力等值线，见图4．对替换段入口处和出口处声压的等值线图二次放大处理，便于清晰观察其等值线的变化情况．图4为马赫数1.8时不同替换段二维模型的数值模拟云图．云图截取的时间节点为1.72s，选取依据为压力等值线密集分布层尾端到达实验段内径的95%，以便观察气体刚离开收缩曲面时压力的分布特点．

图4(a)为等截面激波管替换段的云图，图中气流方向均为从左到右，随着气流方向压力等值线数值逐渐减小．可见，入口处激波的等值线分布呈现碎片状，没有呈现明显的规律性．出口处左侧等值线分布呈波纹状，右侧等值线分布则存在小型闭环，但是等值线分布基本竖直，说明出口气流较为平稳．图4(b)为直线变截面激波管替换段的云图，可见变截面会增加激波管的内部压力．相比于等截面激波管的等值线分布，直线变截面下压力分布的碎片分布显著降低．这是因为口径收缩会导致其内部气体汇聚，使得其碎片状的压力等值线相交．在出口处左侧存在两个闭环，并且其等值线分布也较为密集．这是因为口径收缩使压力变化梯度增大，整体的等值线分布就会更为密集．

图4(c)为基于不可压缩流计算曲面的替换段的云图，其碎片化分布基本消失，呈两条等值曲线分布．入口处等值线向右侧凸起，出口处等值线波纹状减小且呈轻微的右侧凸起，分布更为密集．这是因为曲面收缩可以减缓边界气体流动的突变，减小了漩涡区的生成．因此采用曲面收缩口径可以优化其压力等值线的分布，并减少入口处的碎片化分布．图4(d)为基于经验公式计算曲面的替换段的云图，其入口处相比于等截面激波管的碎片化分布具备了一定的规律性，但是比基于压缩流曲面计算云图的碎片化分布明显，这是因为其在入口处的变化斜率要大于不可压缩流曲面．而其出口处的等值线分布要比不可压缩流云图的分布更加竖直，这是因为其在出口处的变化斜率要比不可压缩流曲面更小．

图4(e)为基于经验公式加计算曲面的替换段的云图，其入口处相比基于经验公式计算曲面的云图的碎片分布较少，这是因为加之后会使得收缩曲面前半段更加平缓．但是其出口处左侧呈向右凸起，右侧等值线分布中闭环曲线减少，形成了向左侧轻微凸起的曲线，说明经验公式加之后可以优化入口处和出口处右侧的等值线分布，但是会导致出口处左侧的曲线有轻微的向右凸起．

图4(f)为基于可压缩流计算曲面的替换段的云图，其入口处等值线的碎片状分布基本消失，并且其整体保持竖直分布，没有出现明显的凸起．这是因为可压缩流在入口处左侧和出口处右侧的变化斜率都很小．其出口处左侧的等值线分布呈轻微的右侧凸起，而右侧的分布还是呈多个闭环的分布，右侧相比于经验公式加并没有形成稳定的层流分布．这是因为可压缩流曲面在出口处右侧形成了一个内凸曲线，从而导致曲线稳定性减弱，所以没有经验公式加的等值线分布竖直度高．

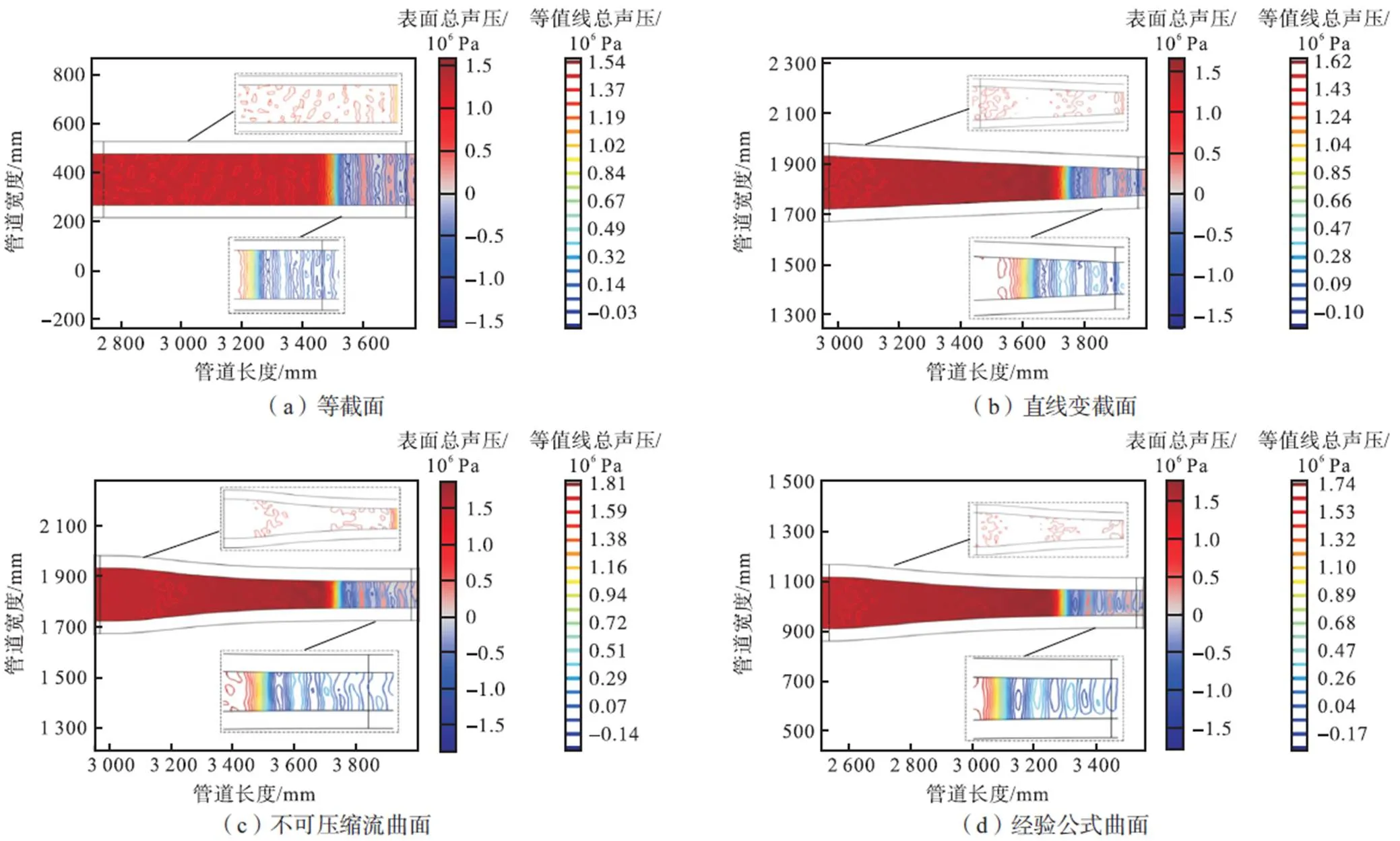
表2总结了马赫数为1.8不同替换段在1.72s时的最大压力值．从表中可知变截面增加了激波管内部压力值，直线对压力值的增加最少，不可压缩流对压力值的增加最多．其余压力值的变化程度相差并不大，这可能是因为收缩曲面下的积分面积基本保持一致，所以总压力变化并不明显．

表2 不同截面类型对应的最大压力值

Tab.2　　Maximum pressure corresponding to different section types

综上所述，在马赫数为1.8的工况下，不可压缩流曲面对应的压力值最大，可压缩流曲面在入口处的等值线分布碎片化最少并且其竖直度最高，经验公式曲面在出口处左侧的等值线分布竖直度最高且其密集度最高，经验公式加曲面在出口处右侧等值线分布形成的闭环分布最少．激波管关注的是其在实验段的等值线分布和压力情况，也就是在保证压力的前提下，出口处右侧的等值线分布竖直度越高越好，所以经验公式加曲面作为替换段更加适合激波管的需求．

3.2 亚音速条件下，变截面对压力分布的影响

在实际激波管中变截面处于不同位置，其内部气流速度可能是超音速或者亚音速，因此对亚音速工况下二维模型进行了数值模拟，以此验证在不同工况下其变化规律的普适性．图5为马赫数为0.8的工况下得到的数值模拟云图，对比发现在亚音速工况下其压力等值线的分布规律同超音速工况下基本一致，证明云图的仿真规律同时适用于亚音速和超音速．因为同超音速云图等值线分布走势基本一致，因此没有全部列出．

3.3 不同曲面长度下变截面对压力分布的影响

通过云图的对比分析认为经验公式加的收缩曲面更适合激波管的变截面设计，但是其替换段长度是根据经验所得．因此，为了研究不同替换段长度对最终压力等值曲线的影响，建立了图6的二维模型进行数值模拟．其中替换段长度分别为500mm、1000mm和1500mm，选取经验公式加曲面作为激波管的替换段内壁面．

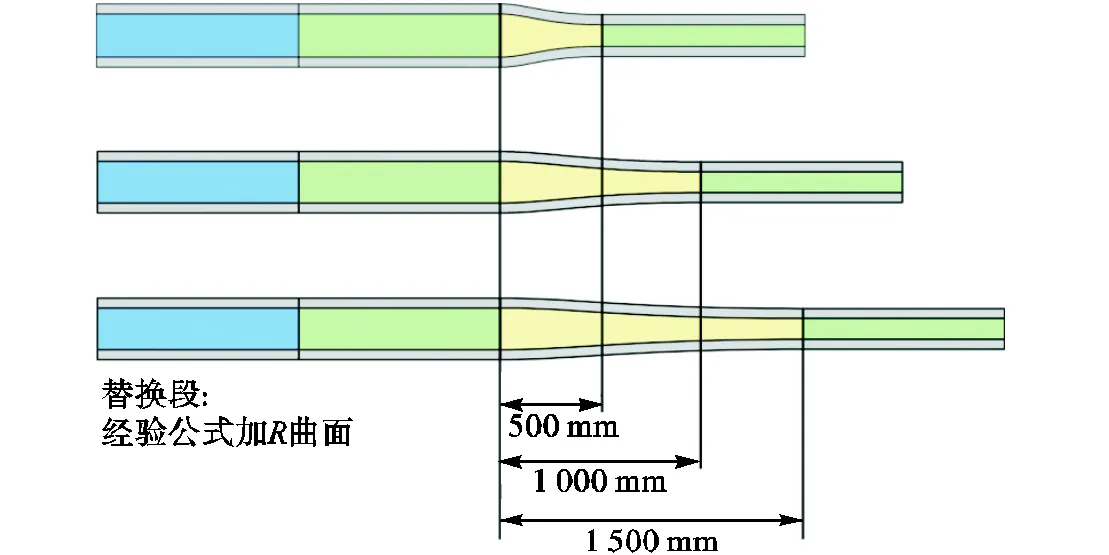
图6 基于经验公式加R理论不同长度替换段示意

图7为替换段长度分别为500mm和1500mm时经验公式加的云图(对应时间节点为1.34s和2.00s)，和图4(e)替换段长度为1000mm时经验公式加云图进行对比，研究替换段长度的影响．由图7(a)可知，其入口处的碎片化分布相比于图4(e)明显减少，但是在入口处右侧的等值线凸起方向从向右凸起变为了向左微凸．这可能是因为替换段长度缩短而变截面直径不变，导致收缩曲面的变化率增大．在出口处左侧等值线右凸更为明显，且右侧的等值线存在较多闭环．

由图7(b)可知，左侧入口端的碎片化分布也更趋向于竖直化，出口处左侧的等值线分布基本完全竖直；相比于图4(e)出口处右侧的等值线分布也基本保持竖直．但是最大压力值为1.69×106Pa，要低于1000mm的最大压力值1.72×106Pa．综合来看，随着替换段长度的增加，压力等值线的分布竖直度更高，但是压力会随之减少．压力的降低可能是因为替换段长度增加而导致的行程压降．

图7 不同长度替换段二维模型的数值模拟云图

4 结 论

随着对实验压力需求的升高，传统等截面设计的激波管可能导致成本过高和技术超纲的问题，而采用新型变截面设计可有效提升激波强度从而产生更高的实验压力5．本文研究了变截面收缩曲面对激波管内部气体流动特性的影响．基于不同理论计算得到了对应的收缩曲面，建立了激波管的二维几何模型．采用有限元分析对模型进行数值模拟，对比分析了超音速和亚音速工况下其内部压力等值线分布规律，并探讨了不同替换段长度对其内部压力分布的影响．主要结论如下：经验公式加曲面作为替换段内壁面能够满足激波管的需求；在超音速和亚音速下激波管的内部压力分布的变化规律基本一致；随着替换段长度的增加，等值线分布竖直度更高，但压力会随之降低．

［1］ Wang Juan，Song Ce，Yuan Rong. CO2emissions from electricity generation in China during 1997-2040：The roles of energy transition and thermal power generation efficiency[J].，2021，773(2/3)：145026.

［2］ 肖华林，罗 坤，金 台，等.航空发动机燃烧室环境中非预混旋流火焰的标量特征[J]. 燃烧科学与技术，2022，28(2)：170-176.

Xiao Hualin，Luo Kun，Jin Tai，et al.Scalar characteristics of non-premixed swirling flames inaircraft-engine combustor environment[J].，2022，28(2)：170-176(in Chinese).

［3］ Zhu Qingyuan，Li Xingchen，Li Feng，et al. The potential for energy saving and carbon emission reduction in China's regional industrial sectors[J].，2019，716：135009.

［4］ 金 武，任超群，汤朝伟，等. 强湍流下甲烷稀燃预混火焰的稳定性研究[J]. 燃烧科学与技术，2021，27(2)：148-154.

Jin Wu，Ren Chaoqun，Tang Chaowei，et al.Stability of lean premixed methane flame under high turbu-nce[J].，2021，27(2)：148-154(in Chinese).

［5］ Singh Digambar，Sharma Dilip，Soni S L，et al. A review on feedstocks，production processes，and yield for different generations of biodiesel[J].，2020，262：116553.

［6］ Wang Kun，Villano Stephanie M，Dean Anthony M. Fundamentally-based kinetic model for propene pyrolysis[J].，2015，162(12)：4456-4470.

［7］ Wang Hai，Xu Rui，Wang Kun，et al. A physics-based approach to modeling real-fuel combustion chemistry-I：Evidence from experiments，and thermodynamic，chemical kinetic and statistical considerations[J].，2018，193：502-519.

［8］ Hanson R K，Davidson D F. Recent advances in laser absorption and shock tube methods for studies of combustion chemistry[J].，2014，44(5)：103-114.

［9］ 何 东，丁艳军，彭志敏. 反射激波后状态分析及对燃料反应进程的影响[J]. 燃烧科学与技术，2022，28(2)：111-118.

He Dong，Ding Yanjun，Peng Zhimin.States analysis behind reflected shock waves and effects on fuel reaction processes[J].，2022，28(2)：111-118(in Chinese).

［10］ 俞鸿儒，林建民，李仲发，等. 扩张激波管流动波图观察[J]. 空气动力学学报，1984(3)：88-91.

Yu Hongru，Lin Jianmin，Li Zhongfa，et al. Observation of flow wave pattern in dilated shock tube[J].，1984(3)：88-91(in Chinese).

［11］ Resler E L，Lin S C，Kantrowitz A. The production of high temperature gases in shock tubes[J].，1952，23(12)：1390-1399.

［12］ Whitham G B. A new approach to problems of shock dynamics(PartⅠ)：Two-dimensional problems[J].，1957，2(2)：145-171.

［13］ Alpher R A，White D R. Flow in shock tubes with area change at the diaphragm section[J].，2006，3(5)：457-470.

［14］ Luo Xisheng，Si Ting，Yang Jiming，et al. A cylindrical converging shock tube for shock-interface studies[J].，2014，85：015107.

［15］ Zhan Dongwen，Li Zhufei，Yang Jianting，et al. Note：A contraction channel design for planar shock wave enhancement[J].，2018，89(5)：056104.

［16］ 林建民，魏以嘉，张大友. 激波管中获得低强度激波的方法[J]. 实验流体力学，2006，20(2)：63-67.

Lin Jianmin，Wei Yijia，Zhang Dayou. A method for obtaining low-intensity shock waves in a shock tube[J].，2006，20(2)：63-67(in Chinese).

［17］ Zaczek L T，Davidson D F，Hanson R K. Determination of the JP10＋OH→products reaction rate with measured fuel concentrations in shock tube experiments[J].，2020，124(16)：3026-3030.

［18］ Fridlyand A，Brezinsky K，Mandelbaum A. N-heptane pyrolysis and oxidation in ethylene-methane and iso-octane mixtures[J].，2013，29(3)：732-743.

［19］ Tranter R S，Lynch P T. A miniature high repetition rate shock tube[J].，2013，84(9)：094102.

Design of Variable Cross Section for Shock Enhancement in Shock Tubes

Bai Shijie，Liang Xingyu，Wang Kun

(State Key Laboratory of Engines，Tianjin University，Tianjin 300350，China)

Compared with the conventional shock tubes with constant cross sections，the design of variable cross section could substantially enhance the incident shock wave intensity. The effect of the contraction surface of variable cross section on the gas flow characteristics inside the shock tube was investigated，which was used in the design of a novel shock tube. Four theoretical approaches，including ideal incompressible one-dimensional flow，compressible flow，empirical equation and empirical equation with，were applied to developing two-dimensional geometric models，respectively，to examine the impact of variable-section contraction surface. The above models were combined with finite element analysis for numerical simulation studies to obtain the contours of pressure distribution under subsonic and supersonic operating conditions，and the effects of different lengths of contraction surfaces were analyzed. The results showed that the contraction surface based on the empirical equation with R was more applicable to the design of variable-section shock tube than the other three theoretical methods.

variable cross section shock tube；contraction surface；compressible flow；finite element analysis；pressure contours

10.11715/rskxjs.R202305032

TK402

A

1006-8740(2023)04-0406-08

2022-08-11．

国家自然科学基金资助项目(52176124，21961122007)；天津市研究生科研创新资助项目(2021YJSB170)．

白世杰(1996—  )，男，博士研究生，bsj@tju.edu.cn.

王 昆，男，博士，教授，kwang5@tju.edu.cn.

(责任编辑：梁 霞)