动水压力对高烈度区大跨度悬索桥阻尼减震性能的影响

郑成成，陈永祁，郑久建

(1.北京工业大学工程抗震与结构诊治北京市重点试验室,北京 100124; 2.北京奇太振控科技发展有限公司,北京 100037; 3.燕山大学建筑工程与力学学院,河北秦皇岛 066004)

近年来,随着我国公路和铁路工程建设加快,跨越库区水系的深水大跨度桥梁越来越多,部分桥梁还位于高烈度地震区。与一般陆上桥梁不同,受水库蓄水影响,库区大跨度桥梁的桥塔(墩)在很长一段时间内浸水深度在5 m以上,在此期间不排除发生地震的可能[1]。尤其对于高烈度区的深水大跨度桥梁而言,地震在使结构产生较大位移和内力响应的同时,可能会引起结构与周围水体发生相互作用并产生动水压力。此外,很多大跨度桥梁常采用黏滞阻尼器进行结构减震,因此,研究动水压力对大跨度桥梁地震响应及阻尼减震效果的影响很有必要。

目前国内外在深水桥梁抗震研究方面已取得一些进展。袁万城等[2]在考虑地震动空间效应的基础上,研究了拉索减震体系的减震效果及动水压力对深水大跨桥梁地震响应的影响;赵秋红等[3]详细分析了水与结构作用机理和分析方法,比较了不同规范中计算动水压力的方法及存在的不足;高立宝等[4]对比研究了不同规范中地震动附加动水质量的差异性和计算精度;LI等[5]基于Morison势流体理论,提出了一种新的流体动力计算简化方法,并通过桥梁模型振动台试验对简化方法进行了验证,研究表明动水压力对深水桥梁抗震的影响不能被忽视;WU等[6]通过考虑桩-土相互作用(PSI)、动水压力及二者的耦联作用,研究了深水高墩大跨连续刚构桥梁的地震易损性;马安财等[7]通过建立考虑动水压力的二自由度的连续梁桥简化模型,研究了动水压力对减震桥梁地震反应的影响。

目前针对高烈度地震区动水压力对深水大跨度桥梁阻尼减震性能的影响研究较少,因此,以一座深水大跨度悬索桥为研究对象,从分析阻尼减震原理和附加动水质量计算方法出发,通过建立不同的桥梁结构体系分析模型,研究动水压力对大跨度悬索桥地震响应和阻尼器减震性能的影响。

1 黏滞阻尼减震设计原理

1.1 黏滞材料耗能机理

黏滞阻尼器主要利用缸体内的液体硅油进行耗能减震。硅油作为一种黏滞材料,在地震作用下的应力和应变之间存在0～π/2的相位差,使其既具有弹性材料储存能量的特性,也具有黏性材料耗散能量的特性[8]。工作滞回曲线如图1所示。

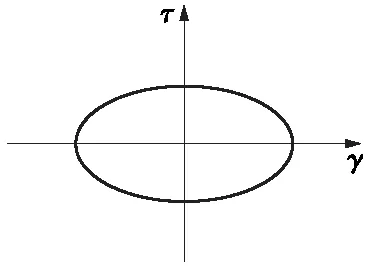
图1 黏滞材料的τ-γ关系曲线

1.2 黏滞阻尼减震原理

阻尼是结构振动衰减的根本原因,但其特性复杂,很难在实际结构中准确计算。在众多阻尼理论中,复阻尼理论和黏滞阻尼理论是目前应用较为广泛的两种线性阻尼理论。然而,复阻尼理论一般只适用于简谐振动或有限频带内的振动分析,由于引入了复刚度,对一般结构动力响应来说计算较为复杂,因此应用不多[9]。黏滞阻尼理论将阻尼理想化为阻尼力与速度成正比的形式,概念清晰且计算简便,在结构分析时可假定阻尼器附加的黏滞阻尼与结构本身的阻尼具有一致性,因此,被广泛应用于桥梁的抗震设计[10]。结构利用黏滞阻尼减震的原理可以通过单质点体系SDOF振动分析来阐明,其运动方程为

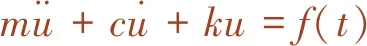
(1)

或

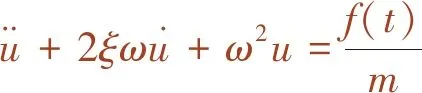
(2)

当f(t)=f0sinθt时,方程的稳态解可表示为

(3)

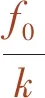
(4)

1.3 黏滞阻尼器理论计算模型

黏滞阻尼器理论计算公式的量化是其在土木工程领域进行实践应用的前提条件。Makris和Constantinou基于Maxwell模型提出了黏滞阻尼器的计算模型并对其逐步进行完善和简化[11-12]。在受迫振动下,液体在阻尼器密封缸体内高速流过阻尼孔的行为,可采用流体动力学Navier-Stokes方程进行描述。对于理想的直阻尼孔,Makris认为可考虑两种极端情况,一种是适用于液体黏度较低、间隙相对较大、液体在小孔流径较短或高流速情况下的惯性流理论。基于此理论,可将Navier方程进行简化,并考虑较低频率情况,而液体加速流过小孔通道产生的惯性力是阻尼力的唯一来源,可用下式表示

P=bp12

(5)

式中,p12为油腔1和油腔2之间的压强差;b为考虑了活塞头面积Ap、活塞杆截面积Ar、小孔面积A1、小孔数量n、控制阀面积A2以及孔隙和调节阀的调节系数Cd1和Cd2的函数。

活塞头两端的压强差可表示如下,其与速度平方成正比关系,因此,当速度很高时阻尼力会急剧增大,不适用于实际工程。

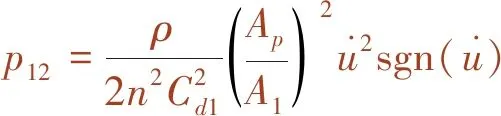
(6)

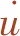
另一种可归纳为适用于液体黏度较高、相对间隙较小、液体在小孔流径较长或低流速情况的黏性流理论。在此情况下,阻尼器响应符合以下计算关系,其消能作用也主要依靠液体流经通道产生的黏性作用来实现。

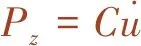
(7)

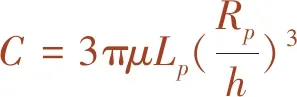
(8)

式中,Pz为黏滞阻尼力;μ为液体黏度;C为阻尼系数;Lp、Rp、h分别为活塞头长度、半径及间隙宽度。

以上分析主要基于阻尼器的几何特性以及液体的本构关系进行讨论。一般采用长直孔的阻尼器只能表现出线性特征,但实际工程中结构在外荷载作用下的动力特性常表现为非线性。因此,为准确描述结构的非线性动力行为,黏滞阻尼器通过采用一系列特殊形状的孔道改变液体的流速特性,使输出的阻尼力与速度的平方不再成比例而表现为非线性。此时,阻尼器的力学性能主要由阻尼系数C和速度指数α决定,影响关系如图2～图4所示,其本构关系可表示为[13]

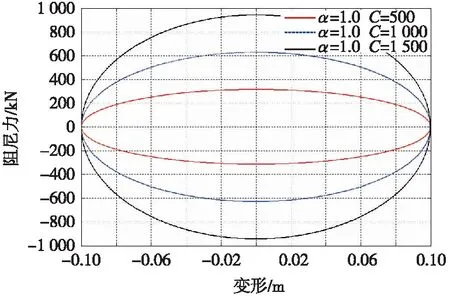
图2 阻尼系数与阻尼器工作性能的关系

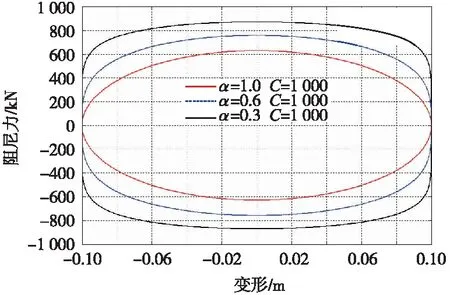
图3 速度指数与阻尼器工作性能的关系

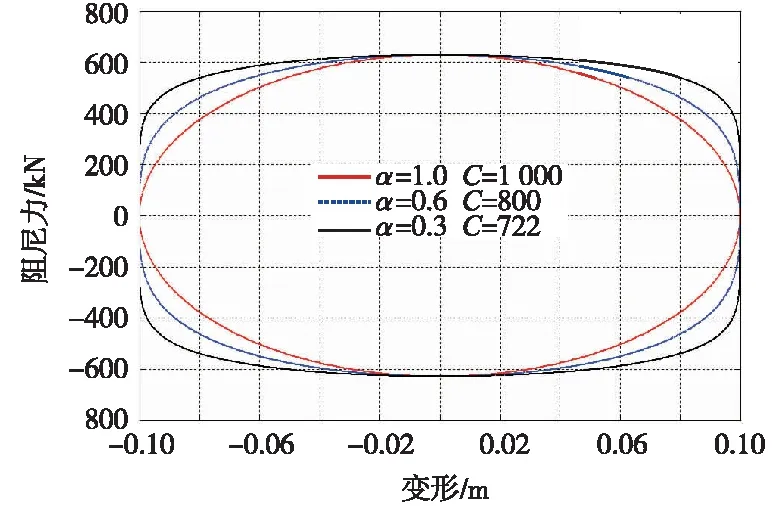
图4 C与α同时变化对阻尼器工作性能的影响

F=CVα

(9)

式中,α为速度指数,常用取值范围在0.3～1.0之间。

2 水与结构相互作用分析方法

水与结构相互作用在桥梁上主要体现为桥墩(塔)与水之间的耦合作用,其本质为桥墩因地震作用产生的受迫振动引起周围水体压力变化,形成了水对桥墩的反作用力和力矩[14]。动水压力对桥墩施加的作用可以表示为桥墩质量矩阵的变化,因此,可以通过附加质量的方式模拟水压力对桥墩的动力作用。目前计算水与结构相互作用的分析方法主要有以下4种。

2.1 基于Morison方程法

Morison方程法假设结构物为刚体,静止刚体和运动刚体在不稳定流中受到的作用力分别为[15]

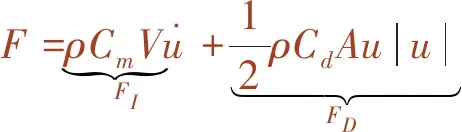
(10)

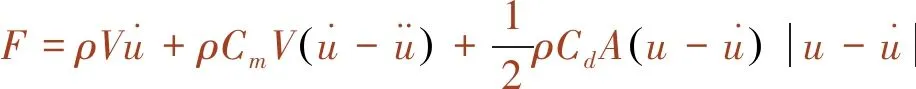
(11)

式中,FI为惯性力,是不稳定流体压力场Froude-Krylov力和附加水惯性力之和;FD为黏性流体的拖拽力。

Morison方程考虑了流体黏性形成的拖拽力,但仅作为一个半经验公式。且从式(10)和式(11)可以看出,Morison方程在实际应用中主要存在2个困难,一是系数Cm和Cd的确定;二是相对速度和加速度的计算。LIU[16]指出,Cm和Cd在实际流体中应该是时间t的函数,此外,雷诺数、表面粗糙程度和边界层情况的影响也不可忽略。然而在实际应用中,为设计方便,常取Cm和Cd为定值。

2.2 解析法

根据水中桥墩需要满足的各种边界条件,通过对流体应满足的三维Laplace方程求解,可求得圆柱形桥墩的解析解如下[17]

ma=(ρwπr2)×

(12)

其中

αm=(2m-1)π/2

(13)

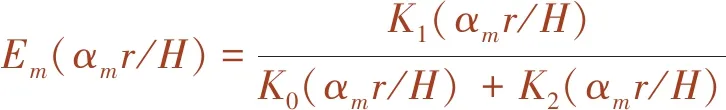
(14)

式中,z为截面距底面的距离;H为水深;ρw为水的密度;r为截面半径;Kn为改进的n阶贝塞尔函数。

对于其他截面形状的桥墩,GOYAL[18]将水域分为内、外两部分,取其间边界为圆柱面,边界内水和结构采用有限元方法离散,边界内建立流固耦合模型,边界上采用解析解得动水压力作为边界条件,从而得到半解析半数值的解法。

此外,赖伟[19]通过推理提出了一种新的计算动水压力的解析方法如下

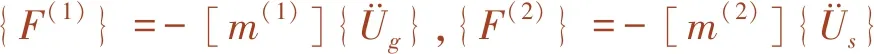
(15)

式中,[m(1)]和[m(2)]分别为水下刚体附加质量矩阵和弹性附加质量矩阵。

[m(1)]是对角阵,其对角元素为

(i=1,2,…,K-1)

(16)

[m(2)]中各元素为

(i=1,2,…,K-1)

(17)

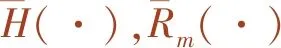
2.3 规范法

GB 50111—2006《铁路工程抗震设计规范》第7.2.7条给出了桥墩浸水深度超过5 m时,受到的地震动水压力计算方法如下

(18)

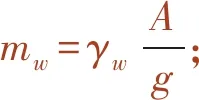
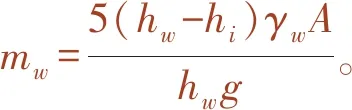
式中,Ci为桥梁的重要性系数;α为水平地震基本加速度;hi为桥墩水下部分高度;H为桥墩整体高度;mw为桥墩单位高度水的附加质量;γ1为桥墩计算方向的振型参与系数;β1为桥墩计算方向的动力放大系数;hw为常水位深度;γw为水的重度;A为桥墩截面面积。

2.4 数值法

数值法以有限元或边界元为主,需要同时建立结构与水的流固耦合模型,并对广泛水域进行离散,计算量较大,一般适合较复杂的流固耦合分析。

3 案例分析

以跨越某库区河流的一座大跨度上承式钢桁梁铁路悬索桥为工程背景,三跨连续加劲梁布置为(110+660+98) m,如图5所示。主缆垂跨比1/10,矢高66 m,仅在主跨660 m区域设置吊索。平行主缆和钢梁主桁的横向中心距均为25 m。主缆和吊索均采用设计强度为1 670 MPa的高强度钢丝。桥塔采用双柱式门式框架结构,截面采用类矩形空心截面形式,其中南塔上塔柱和下塔柱截面尺寸变化如图6所示。南岸桥塔高191 m,北岸桥塔高147 m。主塔采用分离式嵌固式桩基础,桥台采用分离式桥台。两岸均采用隧道锚碇。三跨加劲梁采用全飘浮结构体系,在桥台及桥塔位置设置竖向支座和纵向活动支座,在塔梁间设置纵向黏滞阻尼器。以水库常年蓄水位1 999 m考虑,南岸侧桥塔的水下深度为62.46 m,北岸侧桥塔的水下深度为18.46 m。采用Midas/civil分别建立不考虑动水压力和考虑动水压力作用的计算模型,如图7所示,前5阶自振特性如表1所示。

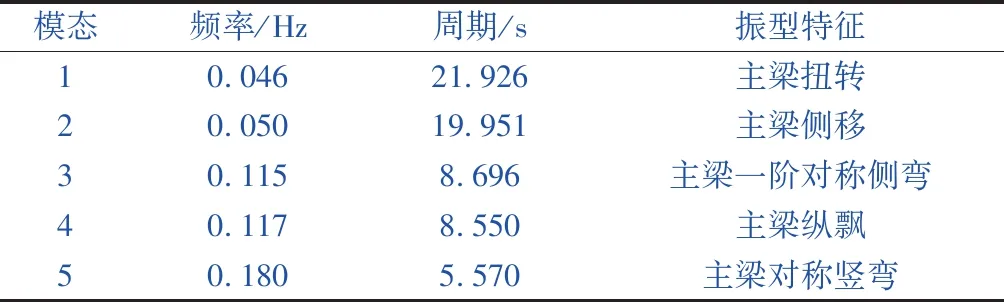
表1 悬索桥自振特性

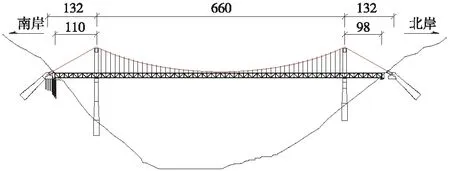
图5 悬索桥总体布置(单位:m)

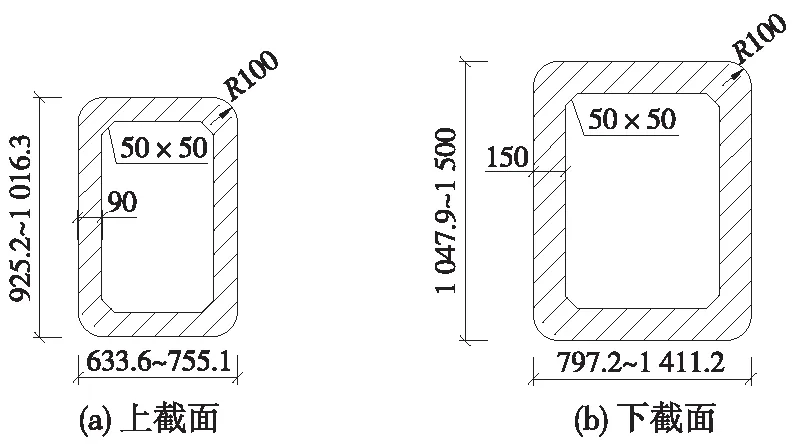
图6 南塔柱变截面尺寸(单位:cm)

图7 悬索桥计算模型

4 计算桥塔附加动水质量

目前计算地震动附加动水质量的方法很多,且各有优缺点。其中基于Morison公式的方法虽较为简洁,但经验成分太多,难以保证计算精度;数值法主要采用流固耦合有限元方法进行计算,不仅理论复杂且计算量很大,难以在实际工程设计中广泛采用;规范法计算简单,但仅适用于圆形或圆端形桥墩;解析法从波动理论出发,通过适当假设,导出桥墩附加动水质量的表达式,是较为推崇的方法之一[20]。综合以上原因,为确定合理的墩水耦合作用方式,分别采用解析法和规范法计算悬索桥南、北两侧桥塔顺桥向的附加动水质量,并进行分析比较,其结果如图8所示。计算结果表明,与解析法相比,采用规范法得到的桥墩顺桥向附加动水质量偏小,最大偏差甚至达到了48%左右。这主要因为规范法是基于经验公式计算的附加动水质量,理论基础不够清晰且未说明用于时程计算时考虑墩水相互作用的影响。因此,将根据解析法的计算结果进行地震作用下悬索桥墩水耦合作用分析,并研究动水压力对黏滞阻尼器减震性能的影响。

图8 计算附加动水质量

5 地震-动水压力耦合响应分析

悬索桥位于高烈度地震区,且由于采用了全飘浮结构体系,钢桁梁在地震荷载作用下的顺桥向位移响应较大,因此,本文主要考虑顺桥向的墩水耦合作用。根据前期计算结果,并综合考虑阻尼器参数对减震效果、阻尼器制造及安装难度、经济性等因素影响后,决定在南、北两侧桥塔与钢桁梁之间各设置4个阻尼系数为4 000 kN·s/m、速度指数为0.3的纵向液体黏滞阻尼器,全桥共计8个。采用安评报告提供的3条100年超越概率3%的地震动时程作为激励荷载(图9),通过分析4种不同工况下的悬索桥地震响应,研究动水压力对结构地震响应及阻尼器减震效果的影响,其中反应最大的一组地震波的计算结果如表2所示。

图9 罕遇地震动时程

由表2结果表明,在塔梁间设置黏滞阻尼器能有效减小钢桁梁的纵向位移,而动水压力作用对钢桁梁的位移响应基本无影响;动水压力增大了桥塔的地震响应,相比对塔顶位移的影响,其对塔顶振动速度的增大效果更明显,不过在主缆拉力约束下,无阻尼减震时的塔顶纵向位移和速度响应也并不十分强烈;由于采用了全飘浮体系,地震作用下的塔梁间相对位移较大,而动水压力进一步扩大了这一影响;剪力和弯矩作为表征桥塔地震内力响应的关键指标,动水压力作用下的塔底剪力和弯矩均有不同程度的增大,其中浸水深度较大的南塔底部剪力最大增幅43.76%(北塔为9.21%),弯矩最大增幅28.12%(北塔为0.48%);主缆作为主要的传力和受拉构件,动水压力使其地震应力响应也有所增大,且表现出北岸侧主缆拉应力比南岸侧主缆拉应力大,这使得北塔顶地震位移响应大于南塔顶位移;动水压力在增大结构地震响应的同时,也进一步增大了减震阻尼器的阻尼力和变形位移。此外,受桥塔浸水深度的影响,动水压力对南岸侧桥塔地震响应的影响比北岸侧桥塔显著。

图10给出了大跨度悬索桥采用不同结构体系时,桥塔水下部分的地震位移响应受水深的影响规律。桥塔底部即浸水最深处的纵向位移为零,随着远离底部约束的距离增加,浸水桥塔受到的整体动水压力越来越大,对桥塔纵向地震位移的增量效应也越来越显著。与无阻尼结构体系相比,设置黏滞阻尼器能在一定程度上减小动水压力造成的桥塔位移,这一现象随着桥塔浸水深度的增加也变得越来越明显,如图11(a)中所示。此外,从图11也可以看出,因塔底土石和塔顶主缆的纵向约束,使桥塔在地震-动水压力作用下的纵向位移自下而上(以无阻尼动水结构体系下的南塔为例,其塔底位移为0 m,塔梁结合处位移为0.53 m,塔顶位移为0.16 m)呈现出先增大后减小的趋势,且最大位移响应靠近塔梁结合处,即桥塔整体位移响应曲线符合“凸”形变化规律。因此,在塔梁结合处设置黏滞阻尼器能对较大的纵向位移起到控制作用。

图10 浸水深度对桥塔位移响应的影响

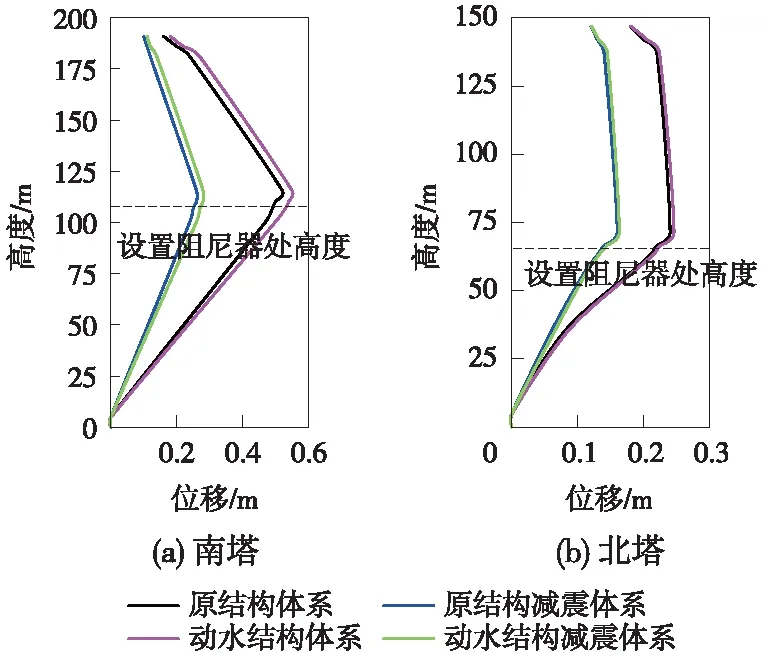
图11 桥塔纵向位移

6 动水压力对阻尼器减震性能的影响

为研究动水压力对黏滞阻尼器减震性能的影响,对设置在南、北岸两侧塔梁间黏滞阻尼器在罕遇地震作用下的工作滞回曲线进行分析,如图12所示。从图12可以看出,阻尼器的滞回曲线较为饱满,说明其工作状态稳定,且因地震强度较大,阻尼器的阻尼力和变形均较大,尤其是设置在塔高更高的南塔与钢桁梁间的黏滞阻尼器。从滞回曲线的包络情况看,动水压力进一步增大了阻尼器的力与位移响应,其中,南塔处阻尼器的阻尼力最大增幅为2.21%,位移最大增幅为8.33%,北塔处阻尼器的阻尼力最大增幅为0.26%,位移最大增幅为4.26%。由于南岸侧桥塔浸水深度接近北岸侧桥塔的3.4倍,使其受到的动水压力影响更大。而黏滞阻尼器作为主要的受力和耗能构件,承受着很大的地震能量冲击,特别在高烈度地震区,一旦受力或变形超限,阻尼器很可能发生破坏(密封失效而漏油),导致减震性能下降。因此,对于地震-动水压力作用显著的深水大跨度桥梁,在采用黏滞阻尼器耗能减震时,不能忽视动水压力对阻尼器工作性能的影响,必须预留一定的安全储备空间。

图12 动水压力对阻尼器变形及阻尼力的影响

阻尼是结构振动衰减的根本原因,而阻尼比作为表征结构耗散振动能量的基本特性之一,直接影响着结构的动力行为[21]。黏滞阻尼器通过黏滞材料吸收地震能量,附加给结构额外的阻尼比来增强结构的抗震能力。为研究动水压力对阻尼比的影响,采用应变能法分别计算了无动水压力和有动水压力作用的减震桥梁结构附加阻尼比,如图13所示。从图13可以看出,在动水压力作用下减震桥梁结构的阻尼耗能Ed在整个能量体系中的占比有所增加,由36.9%上升至38.0%,附加阻尼比也由0.047 8上升到0.049 9,增幅在4.39%左右。附加阻尼比的增大,一方面说明动水压力进一步激发了黏滞阻尼器的耗能能力,另一方面也表明黏滞阻尼器能对地震动水压力引起的结构振动做出反应,并通过附加阻尼的方式加速振动衰减。

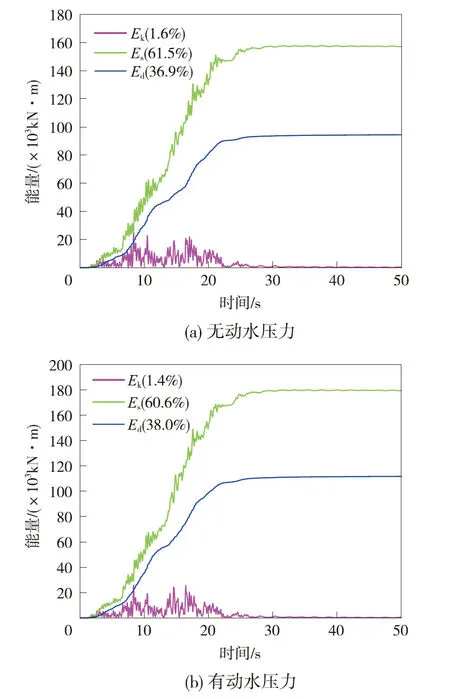
图13 地震能量响应时程曲线

7 结论

采用附加质量的方式,研究了地震动水压力对高烈度区大跨度深水悬索桥结构地震响应和黏滞阻尼器减震性能的影响,得到如下结论。

(1)地震激发的动水压力进一步增大了桥梁结构的地震响应。相比结构位移,动水压力对桥塔的内力响应影响更大,且随着浸水深度增加变得愈加明显。

(2)动水压力的存在进一步扩大了阻尼器减震时的工作滞回面积。相比阻尼力,动水压力对阻尼器变形位移的增幅效果更显著。因此,深水大跨度桥梁在采用黏滞阻尼器进行结构减震时,应考虑地震动水压力的影响,避免阻尼器发生超限破坏。

(3)在理论层面上详细分析了阻尼器基于黏滞阻尼原理用于高烈度地震区大跨度悬索桥抗震的可行性。讨论了实际工程中计算深水桥梁墩水耦合作用的有效方法。在地震动水压力影响评估、阻尼器参数设计与安置等方面,为类似深水大跨度悬索桥的减震方案制定提供参考。

由于在计算时采用了一致地震激励,未考虑“V”形峡谷地形对地震动空间变化的影响,桥梁地震响应结果存在一定误差。