高压电缆源平移扫描CT 高效重建算法

倪松，陈杰，余海军，段晓礁，陈大兵，刘建军

（1 重庆真测科技股份有限公司，重庆 401332）

（2 国网江苏省电力有限公司电力科学研究院，南京 211103）

0 引言

交变聚乙烯（Cross-Linked Polyethylene，XLPE）高压电缆因其出色的性能被广泛用于城市供电系统中。受工作环境、温度以及压力的影响，电缆内部阻水缓冲层易发生烧蚀缺陷导致电缆出现故障，严重影响输电安全［1-3］。

目前，局部放电检测技术［4-6］是电缆缺陷检测常用方法之一，但此技术容易受外部环境影响，在实际电缆缺陷检测中受到一定限制。X 射线数字成像技术广泛用于各领域无损检测中［7-8］，但其在一个方向上对物体进行扫描，其图像反映的是该方向上物体结构叠加的信息，结构层次性较差，只能用于检测较为明显的缺陷。X 射线计算机断层扫描（Computed Tomography， CT）技术通过对物体进行不同方向上的扫描，能清晰成像物体内部结构［9-10］。射线源平移扫描局部CT 成像方法（Local Source-Translation Computed Tomography，L-STCT）［11］针对城市地下隧道中电缆检测，该方法射线源沿直线运动，通过重建图像判别是否存在缓冲层烧蚀缺陷。由于L-STCT 主要对电缆局部扫描成像，射线无法覆盖整个电缆从而导致数据截断。同时，由于射线源移动距离和探测器宽度有限，无法实现至少180o投影角覆盖，存在有限角度成像问题。因此，L-STCT 扫描重建是一个包含数据截断和有限角成像的复合问题。

目前常用的图像重建方法主要分为解析类和迭代类算法。对于数据截断或有限角成像，文献［11］中使用联合迭代重建算法（Simultaneous Iterative Reconstruction Technique，SIRT）获得了较好的结果，类似的还有联合代数重建方法［12］、各向异性的全变分方法［13］以及高阶全变分最小化方法［14］。多次迭代重建过程得使得迭代类算法计算量大，重建速度较慢。解析类算法速度更快，但数据存在截断或缺失时容易产生严重的伪影，比如经典的滤波反投影算法（Filtered Back-Projection，FBP）［15］。OHNESORGE B 等提出了一种直接插值补全截断投影数据的方法［16］，类似的在文献［17， 18］中也得到了应用。此外，针对数据插值误差较大的特点，提出了利用深度学习网络结合先验知识来补全数据，从而缓解截断并提高插值精度［19-21］。QUITO E T 等分析了产生有限角伪影的原因［22，23］，并提出一种投影数据平滑处理方法来抑制有限角伪影。

本文提出一种基于数据平滑的局部扫描重建（Local-detecting FBP， LFBP）算法用于L-STCT 扫描重建。数据平滑主要利用余弦函数沿探测器和射线源方向分别进行数据插值。在探测器两端向外插值，新增部分逐渐平滑到零的虚拟数据与原始投影数据进行拼接，从而避免数据在探测器两端突然降为零，起到缓解数据截断的作用。类似地，从射线源采样起始和终止点采集的数据开始，对射线源在靠近其移动轨迹两端采集到的部分原始数据进行平滑处理，处理后的数据沿着射线源轨迹的两端逐渐平滑到零，起到抑制有限角伪影的作用。

1 扫描模型及重建算法

1.1 扫描模型

L-STCT 采用射线源平移直线扫描，成像模型如图1（a），扫描过程中，射线源和探测器置于待测电缆两侧，探测器和电缆固定不动，射线源平行于探测器做等距平移，并在每个位置发射锥束射线照射电缆。为了便于分析，取过射线源轨迹并垂直于探测器的平面为研究对象，得到图1（b）所示的L-STCT 二维几何模型。根据之前的研究［7］，在L-STCT 系统的扫描空间中，分别连接探测器上端点与射线源轨迹下端点、探测器下端点与射线源轨迹上端点，两线交点Q处可得到最好的成像质量。因此，以Q点为原点建立笛卡尔直角坐标系，其中x轴平行于射线源轨迹指向上，y轴指向探测器中心并垂直于探测器。由于电缆直径过大，难以全局成像，故将电缆中心o'相对坐标原点o向x负方向偏移距离τ，使待观测的缓冲层位于成像质量最好的Q点附近，仅对该区域进行局部成像。

图1 L-STCT 扫描模型Fig. 1 L-STCT scanning model

基于此，扫描过程中，探测器单元的坐标可表示为

射线源焦点的坐标可表示为

式中，u为探测器单元的局部坐标，δ为射线源焦点位置的局部坐标，d为探测器宽度的一半，s为射线源移动轨迹长度的一半，h和l分别表示原点o到探测器的距离和射线源轨迹到原点o的距离，有

F表示射线源轨迹到探测器的距离。在扫描系统中，任意一条射线可由其与y轴的夹角φ以及该射线与坐标原点o的距离r指定。沿射线对路径上各点的衰减系数f(x，y)进行积分即为该射线指定的投影，即

在L-STCT 扫描系统中，任意射线也可由(δ，u)进行唯一指定，有

根据图1（b）所示的几何关系，(r，φ)与(δ，u)的坐标对应关系为

根据式（7），想要采集至少180o的投影数据以实现精确重建，需要δ的取值范围达到( -∞，+∞)。但在实际扫描过程中，射线源移动距离2s必然有限，因此L-STCT 成像是一个有限角度问题。同时，由于电缆直径过大，射线源在每个位置发出的射线都只能覆盖电缆的一部分，探测器采集到的投影数据是截断的，L-STCT 成像是一个有限角和数据截断复合问题。

1.2 LFBP 重建算法

虽然FBP 算法往往受不完备数据的影响显著，但其在重建效率上的优势仍使FBP 算法有极大的研究价值。L-STCT 扇形束扫描的FBP 算法可利用变量替换从经典的平行束FBP 算法中推导，结合图1（b）所示的L-STCT 扫描模型，经典的平行束FBP 重建算法可表示为

将式（6）、（7）、（8）和（11）带入式（9）并化简可得

式（12）即为L-STCT 扇形束扫描的FBP 重建公式。由于L-STCT 扫描重建是一个包含了有限角和数据截断的问题，直接使用式（12）重建有限角度且截断的投影数据p(δ，u)会在重建图像中引入严重的条状伪影。受处理数据截断和有限角成像相关方法的启发，针对同时存在数据截断和有限角成像问题的L-STCT 扫描方式，对应地提出一种数据平滑策略，从而抑制有限角和截断伪影，提高重建图像质量。

为缓解数据截断造成的截断伪影，对投影数据沿探测器两端向外进行插值平滑。定义M和N分别表示每行探测器单元阵列个数和射线源采样点数，探测器单元u接收射线源位置δ发出的射线得到投影数据值p(δ，u)，取不同的δ和u形成数据矩阵p，其维度为M×N，定义向外插值M'列虚拟平滑数据。数据外插平滑过程中，首先分别提取原始数据最左侧一列数据p( ⋅，u1)和最右侧一列数据p( ⋅，uM)进行向外插值平滑处理，可表示为

式中，平滑函数g(x)=cosx，其中。pL( ⋅，um)和pR( ⋅，um)分别为左右两侧数据插值产生的虚拟平滑数据，。平滑后的原始数据可表示为

可以看出，数据向外插值平滑在原始数据基础上增加了部分虚拟数据。其次是对投影数据沿射线源采样方向进行向内插值平滑，从而抑制有限角成像导致的伪影。定义向内插值N'行数据进行平滑处理，平滑后的数据可表示为

图2 数据平滑过程Fig. 2 Diagram of projection smoothing

式（16）即最终用于L-STCT 扫描的LFBP 解析重建公式。

2 模拟仿真

为了验证本文算法针对L-STCT 扫描重建的有效性，设计了仿真实验。以110 kV 和220 kV 两种型号电缆为实验对象，对应的结构尺寸分别为Ø100 mm 和Ø160 mm，其内部结构基本一致。在材料方面，220 kV 内部阻水缓冲层为铜丝纤维编织布，而110 kV 为普通聚酯纤维编织布，其他基本相同。根据电缆的内部结构，设计了如图3 所示的仿真模体，并根据实际情况模拟了潜在的缓冲层缺陷。模体大小为512 pixel×512 pixel，由Intel（R） Core （TM） i7-4790 CPU 3.6 GHz×8、NVIDIA GeForce GT 720、8 GB RAM、Windows10 专业版64 位计算机在MATLAB R2018b 环境下完成。

图3 电缆仿真模体Fig. 3 Simulation phantom of cable

实验主要针对电缆局部进行扫描重建，重建图像大小为300 pixel×300 pixel，分别使用SIRT、FBP 和LFBP 方法进行图像重建对比。SIRT 方法重建时，相关重建参数与之前工作［7］中一致，共迭代500 次。FBP 方法直接使用原始数据重建。LFBP 方法重建时，数据平滑参数M'设置为50，N'设为100。采用均方根误差（Root Mean Square Error， RMSE）和结构相似性（Structure Similarity Index Measure， SSIM）来进行定量评价，RMSE 表征重建图像和原始模体之间的偏差，SSIM 表征重建图像与原始模体的结构相似度，其具体定义为

式中，f为重建图像；?为原始模体；分别为重建图像和原始模体的像素平均值；M和N分别为重建图像的行和列；σf和分别为重建图像和原始模体的标准差；为协方差；C1和C2是常数项。一般RMSE 值越小，SSIM 值越高，重建图像质量越好。

由于电缆内部铜芯密度高，射线难以穿透，且电缆缺陷多集中在缓冲层的一侧，因此主要成像电缆易产生缺陷的局部区域。针对实际的检测需求，对电缆Ø100 mm 和Ø160 mm 两种型号进行扫描重建仿真，参数如表1 所示。两种电缆除尺寸不同外，其内部结构基本一致，且产生的缺陷类型也基本一致，因此通过设置不同的模体尺寸进行仿真。

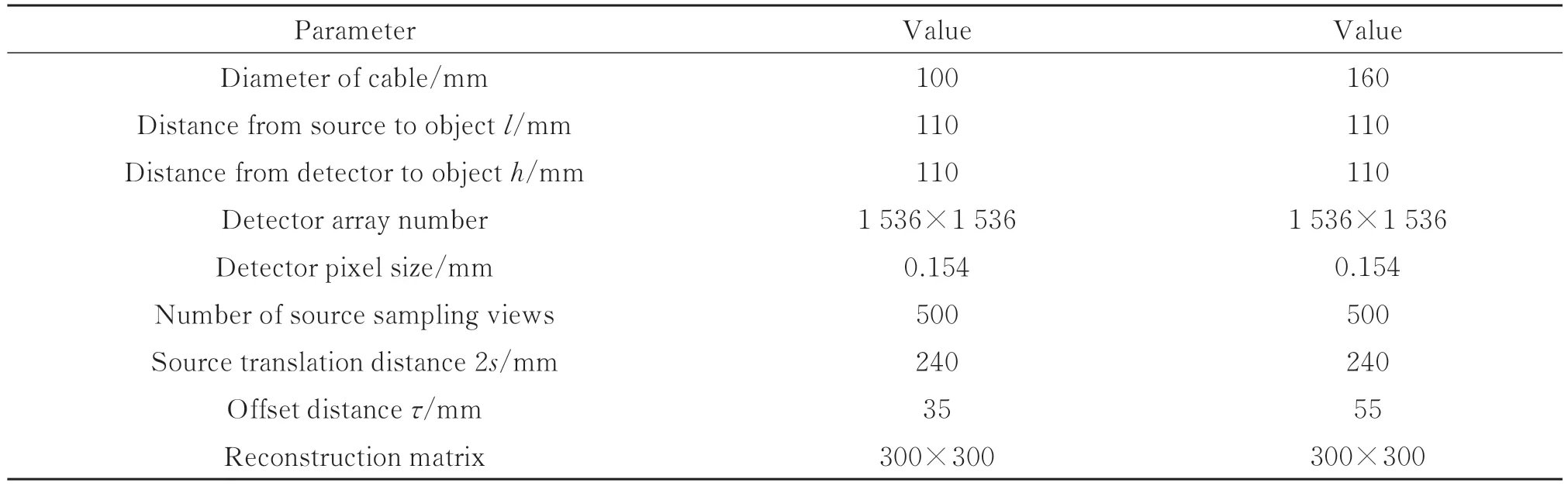
表1 仿真参数Table 1 Parameters for simulation

图4 展示了两种电缆通过不同重建方法得到的局部重建结果。所提的LFBP 方法和SIRT 重建图像质量接近，均优于FBP 重建结果。由于数据截断和有限角问题，FBP 重建结果如图4（a）所示，出现了明显的截断伪影（图中红色箭头所示）和有限角伪影（图中绿色箭头所示），干扰了几何结构以及缺陷的识别。SIRT算法通过500 次迭代得到的重建结果中，截断伪影被明显抑制，图像清晰度提升，但有限角伪影依旧明显（图4（b））。LFBP 方法使用经平滑处理后的投影数据重建，其结果如图4（c）所示，图像中无明显截断伪影，与SIRT 重建图像质量相当。相较于FBP 和SIRT 重建图像，有限角伪影也得到了抑制。

图4 FBP、SIRT、LFBP 三种方法仿真重建结果Fig. 4 Simulated reconstructions of FBP， SIRT and LFBP methods

为了进一步对比不同算法重建图像的差异，提取重建图像第150 行中第1 到160 号像素与模体图像进行灰度对比，如图5 所示。由于数据截断产生的条纹截断伪影使得FBP 重建图像对应的灰度值曲线出现明显波动，偏离了真实值。SIRT 重建结果对应的灰度值曲线明显更加平滑，贴近于真实值。但由于有限角伪影影响，仿真的高密度电缆外部铝护套重建灰度值偏低，而在其他低密度且没有受到伪影影响的区域重建灰度接近原始模体。LFBP 重建由于综合考虑了数据截断以及有限角问题，重建图像灰度值和SIRT 结果接近，并且由于抑制了部分有限角伪影使得其在高密度外围铝护套图像重建灰度值比SIRT 更加贴近真实值，但在低密度区域重建灰度值偏差略高于SIRT 重建结果。

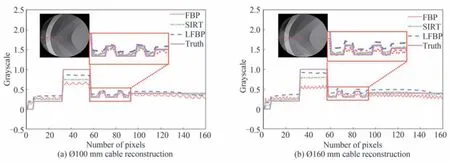
图5 不同方法重建图像第150 行局部区域灰度图Fig. 5 Profiles along 150th row of image reconstructed by different methods

为了进一步比较图像质量，表2 给出了根据不同方法重建结果计算的量化指标。结果显示LFBP 重建图像质量和SIRT 接近，且明显优于FBP 重建图像。对比RMSE 值，SIRT 和LFBP 指标明显低于FBP，说明重建图像与模体间的误差更小。同时，由于直接FBP 重建导致的伪影覆盖了电缆的结构特征，其SSIM值低于其他两种算法。

表2 不同方法重建图像量化指标Table 2 Quantitative evaluation metrics for different methods

表3 对比了不同算法的重建时间。可以发现解析重建方法FBP 和LFBP 的重建效率相当，比SIRT 迭代算法快约45 倍。由于对原始投影数据进行向外插值50（M'=50）列的平滑数据，额外增加了约1/15 的虚拟数据，因此LFBP 重建时间较直接使用原始数据重建的FBP 方法略有增加，但仅0.04 s 的差距几乎可以忽略。结合上述对重建图像质量和重建时间的对比，可以发现LFBP 既保证了重建效率与FBP 相当，同时成像质量与SIRT 迭代重建相当。

表3 三种方法重建时间对比Table 3 Time consumption for different reconstruction methods

3 实验验证

为了验证算法的有效性，搭建了如图6 所示的实验平台，包含X 射线源（L10321， Hamamatsu， 日本）、平板探测器（PaxScan1313DX， Varian， 美国）、平移台（M-ILS250PP， Newport， 美国）和待测电缆样品。射线源允许的最大管电压和管电流为100 kV 和200 μA；平移台最大行程为250 mm；探测器阵列包括1 024×1 024 个探测器单元，单元尺寸为0.127 mm×0.127 mm。射线源安装在平移台上，实际扫描过程中由平移台带动射线源直线运动，待测电缆和探测器固定不动。由于两种电缆尺寸不同，对Ø100 mm 电缆设置射线源工作电压电流为70 kV 和110 μA，对Ø160 mm 电缆设置射线源工作电压电流为100 kV 和110 μA。其他参数与仿真一致。

图6 实际实验平台Fig. 6 Practical experiment platform

图7 展示了Ø100 mm 和Ø160 mm 电缆分别使用FBP、SIRT 和 LFBP 方法重建的结果。由于实际扫描重建时需读取扫描数据，重建时间略高于仿真实验，分别为2.5 s、64.8 s 和2.7 s。LFBP 和FBP 重建效率相当且明显高于SIRT 算法。由于投影数据存在截断和有限角问题，直接使用FBP 算法重建导致了严重的截断伪影和有限角伪影，对电缆缺陷的识别造成干扰。SIRT 重建结果有效地抑制了截断伪影，增强了电缆结构的识别度，但无法进一步处理有限角伪影。LFBP 重建结果显示，不仅截断伪影得到了有效地抑制，而且弱化了有限角伪影，减小了其对真实几何结构的影响。

图7 不同方法重建结果Fig. 7 Images reconstructed by different methods

为了进一步展示所提方法对伪影的抑制效果，以Ø100 mm 电缆为例，对比了不同位置横截面有无伪影的重建结果。结果显示，所提出的重建方法能有效抑制截断伪影，并弱化有限角伪影。进一步对比缺陷处细节放大图像，第一排没有进行伪影抑制的图像中，缺陷淹没在伪影里难以识别。第二排经过伪影抑制后的图像，能从细节放大图中清楚地看到电缆缓冲层的烧蚀缺陷（如图8 黄色箭头所示）。实验充分反映了在电缆缺陷检测中进行重建图像伪影抑制对缺陷识别的重要性。

图8 Ø100 mm 电缆不同位置截面重建有无伪影结果对比Fig.8 Comparison of image with and without artifacts suppression for different layers of Ø100 mm cable

在实际扫描过程中，针对Ø100 mm 和Ø160 mm 两种型号电缆，提取了射线覆盖范围内电缆不同位置横截面的投影数据，从而重建出不同位置的截面图像。尽管电缆几何结构在其长度方向上是一致的，但其内部的缺陷分布和数量是不同的。通过重建不同位置的切片图像既增大了发现缺陷的概率，也可以对电缆在长度方向上存在缺陷的部分进行定量分析。图9 展示了使用LFBP 方法对两种型号电缆的不同高度截面进行重建的结果，红色箭头所示为检测出的缓冲层烧蚀孔洞缺陷。重建的电缆局部截面结构清晰可见，使用该方法能较好地抑制伪影，从而有效地检出缺陷，满足实际需求。实验进一步验证了所提方法针对不同型号电缆缺陷检测的有效性，有望直接用于实际电缆三维解析重建中。

图9 不同位置投影数据LFBP 重建结果Fig. 9 Images reconstructed by LFBP method with projections at different locations

4 结论

本文提出一种基于数据平滑的高压电缆X 射线扫描图像解析重建方法（LFBP）。在处理截断伪影时，采取了数据向外插值平滑的策略，增加了部分虚拟数据，在重建过程中起到抑制截断伪影作用。在处理有限角伪影时，对投影数据采用向内平滑的策略，对射线源在移动轨迹两端采集的部分原始采样数据进行了平滑处理，在重建过程中对有限角伪影有一定的抑制作用。实验结果表明，直接使FBP 重建会产生严重的有限角伪影和截断伪影，LFBP 能有效抑制两种伪影且重建效率基本相同；SIRT 通过较长时间的迭代，较好地抑制了图像伪影，但LFBP 能有效缩短重建时间且图像重建质量相当。综上，LFBP 重建方法能兼顾重建效率和重建图像质量，可推动L-STCT 扫描方式应用于实际电缆检测。