基于小波时频分析的车轮多边形和轨道不平顺分析研究

孙亮　张建全　沈龙江　贺世忠

摘要：车轮多边形和轨道不平顺是当下影响地铁车辆运行品质的最主要原因。轴箱的振动是轮轨耦合振动的最直接反映，车轮多边形引起的周期性激励和轨道不平顺信息可以从轴箱振动信号中分析出来。本文使用西门子Simcenter TestLab振动控制采集分析系统采用小波变换对实测轴箱振动信号进行时频分析，得到车轮多边形引起的振动主频在59.81～88.45 Hz的范围内，本方法可快速得到被测车辆车轮多边形情况以及定位轨道不平顺较为严重的区段，为工程师分析车辆异常振动提供依据。使用小波变换对轴箱振动信号进行时频分析的方法相较于传统车轮和轨道测试手段更为方便可靠。

关键词：小波变换；时频分析；线路不平顺；车轮多边形；轴箱振动分析

中图分类号：TE991.8 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.04.008

文章编号：1006-0316 （2023） 04-0053-06

Research on the Wheel Polygon and Track Irregularity based on

Wavelet Time-Frequency Analysis

SUN Liang1，ZHANG Jianquan1，SHEN Longjiang1，2，HE Shizhong1，2

（ 1.CRRC Zhuzhou Locomotive Co.， Ltd.， Zhuzhou 412001， China; 2.The State Key Laboratory of

Heavy Duty AC Drive Electric Locomotive Systems Integration， Zhuzhou 412001， China ）

Abstract：Wheel polygons and track irregularities are the most important reasons that affect the running quality of metro. The vibration of the axle box is the most direct reflection of the coupling vibration of the wheel and rail. The information of the periodic excitation and track irregularities caused by the wheel polygon can be analyzed from the vibration signal of the axle box. In this paper， the Siemens Simcenter TestLab vibration control acquisition and analysis system is employed to conduct the time-frequency analysis with wavelet transform on the axle box vibration signal， which shows that the main frequency of vibration caused by the wheel polygon is in the range of 59.81-88.45Hz. Though this method the wheel polygon situation of the tested vehicle and the section with severe positioning track irregularity can be quickly obtained， which provides a basis for the engineers to analyze the abnormal vibration of the vehicle. The time-frequency analysis of the axle box vibration signal is more convenient and reliable than the conventional wheel and track test methods.

Key words：wavelet transform；time-frequency analysis；track irregularity；wheel polygon；axle box vibration analysis

近年来，地铁车辆的转向架附属支架经常出现开裂的问题，相关研究机构对此问题展开了众多研究。相关研究表明轨道车辆转向架的振动异常是支架开裂的直接原因，目前学界主要认为轨道不平顺、车轮多边形是异常振动的源头。国内外学者对此展开了大量的研究。Alfi等[1]利用车辆－轨道耦合动力学模型，通过输入实测车辆振动加速度和轴箱加速度值，预测波长大于20 ｍ的轨道不平顺。Weston等[2]實测车辆轴箱加速度分析出了轨道高低不平顺的位置。Li等[3]采用BP神经网络的方法对轨道不平顺与车辆振动响应的关系进行研究。关于车轮多边形形成的激励目前尚不明，但是严重的车轮多边形会引起车辆振动特性异常，损害车辆结构安全[4-6]。李伟等[8]认为车轮多边形的与是轮对一阶弯曲模态有关，陈光雄等[9]认为车轮多边形磨耗与轮轨系统的低频黏－滑振动有关，胡晓依等[10]通过建立车辆轨道耦合动力学模型，验证了多边形磨耗与“频率固定”激励相关。各种理论都认为车轮多边形无法消除，只能通过在早期干预，减缓多边形发展。想要在车轮多边形磨耗早期发现，就必须对车轮多边形进行检测，车轮多边形的检测一直比较麻烦，通常采用车轮粗糙度测量系统，但该系统需要在库内顶起轴箱，影响车辆正常运营。所以一种通过轴箱振动检测车轮多边形的方法是解决多边形检测问题的有效手段。

小波变换是一种线性变换方法，适用于像轴箱振动信号这种线谱成分复杂、带宽分布广以及噪声多的非稳定信号，相比于短时傅里叶变换，其窗口大小可随频率变化，具有高灵活性、高对比度和高分辨率的优点。基于此，本文采用基于小波变换时频分析方法分析实测的地铁轴箱振动信号，准确判断地铁车辆车轮多边形和线路轨道不平顺情况，为车辆异常振动分析提供支撑。

1 小波变换基本原理

小波变换[7]通过一个随频率大小伸缩的小波函数的平移实现对频率域的局部化分析，小波函数在信号高频区域对时间进行细分，在信号低频区域对频率进行细分，可自适应时频信号处理的要求，是理想的信号处理工具。

2 轴箱振动实测信号原始数据

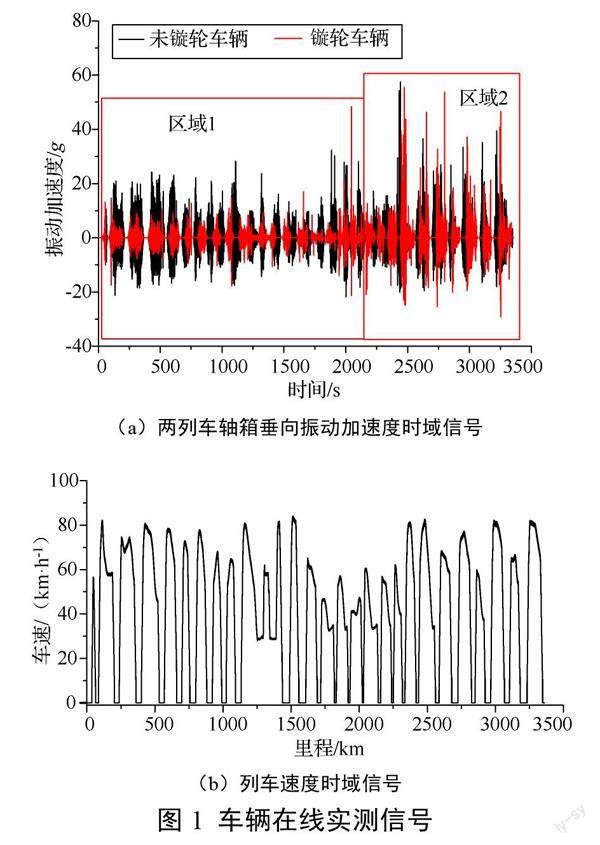
轴箱振动时域信号能够综合反映出车辆运行过程中的线路情况和车轮状态。图1（a）展示了两列车在同一线路上运行轴箱垂向振动加速度时域信号，一列为镟轮后车辆，另一列为未镟轮车辆，每一小段信号代表车辆从一个站点运行至下一站点的振动信号。从图中可以清晰的看出整个线路振动信号分成两个区域，区域1内的振动普遍要小于区域2，说明区域1的线路条件要优于区域2。在区域1内，镟轮后车辆的轴箱振动幅值要小于未镟轮的车辆，在区域2内，两者振动幅值相近。图1（b）展示了列车的速度时域信号，两列车的速度控制信号一致。

3 实测信号时频分析

使用西门子Simcenter TestLab振动控制采集分析系统采用小波变换对实测轴箱振动信号进行时频分析，可以得出每段信号频率成分随时间变化规律，根据车辆运行机理，随时间连续变化的频率成分是由车轮转动激发的谐振，随时间不连续的频率成分则是由环境（轨道、侧风等）所激发。

图2为两列车辆在区域1内某两段线路的轴箱振动时频图，该图横轴为时间，纵轴为频率，通过颜色表示幅值，颜色越深，幅值越大，从图中右侧的幅值图例中可知设置的阈值是1g2/Hz，大于阈值的幅值都显示为黑色。图2（a）为未镟轮车辆的轴箱振动时频图，从中可以看到振动信号在横向成带状分布，说明轴箱振动信号中存在谐振信号，该信号在时间上呈现连续性且变化趋势与车辆速度成一致性，这一现象为典型车轮多边形特征。这些带状条纹间距约为7 Hz，同时在59.81～88.45 Hz的范围内，且呈现出深紫色，由车辆运行速度与车轮多边形引起的振动频率关系（式（7））可推导出引起上述频率范围的车轮多边形阶数（式（8））：

式中： 为轴箱振动频率，Hz； 为车辆运行速度，km/h；λ为车轮多边形波长，mm； 为车轮直径，mm；n为车轮多边形阶数。

从图2（b）中得到的270～340 s的车辆运行速度约为65 km/h，该车已运营6年左右，车轮的平均直径约为800 mm，则通过式（8）可以算出59.81～88.45 Hz振动是由8～12阶多边形引起。

图2（b）为镟轮车辆的轴箱振动时频图，可看出轴箱振动整体更弱，且横向带状条纹不清晰，车轮多边形状态良好。因此在区域1内两者振动差异主要是由于车轮多边形差异引起。

图3为两列车辆在区域2内某两段线路的轴箱振动时频图。通过上文的分析可知，镟轮后的车辆车轮多边形的情况较好，所以影响其轴箱振动的主要原因是线路不平顺。图3（b）为镟轮车辆的轴箱振动时频图，分别截取了2400～2500 s和2700～2800 s的振动时频图，从中可以看到间隔相等的竖向带状条纹，这表示轴箱收到固定时间间隔的冲击信号。从图2（b）中得到的2710～2790 s的车辆运行速度约为75 km/h，计算可知引起这些竖向条纹的冲击空间间隔约为25 m，考虑为轨道焊接接头不平顺引起的冲击。图3（a）为未镟轮车辆同样在2400～2500 s和2700～2800 s的的轴箱振动时频图，图中可以看到时频图呈现同时横向竖向带状条纹，且横装条纹的能量比区域1更高，频带更宽。不难理解，在轨道接头冲击的条件下，轮轨耦合振动被激发，叠加车轮多边形磨耗，车辆运行品质严重恶化，60～120 Hz范围内存在谐振成分。可以很明显地发现在2430～2460 s之间存在宽频的剧烈振动，此处推测为轨道轨面磨损引起的振动。

4 车轮多边形和线路不平顺验证

选取未镟轮车辆二位轮对测试车轮多边形，结果如图4所示。图4（a）采用指教坐标表示车轮不圆度情况，横轴表示车轮周向展开后的位置，纵轴表示车轮实际直径与标准直径的差值，从测量结果来看，车轮圆跳动最大值为0.23 mm。图4（b）采用极坐标表示车轮不圆度，本质上与图4（a）相同。图4（c）和图4（d）分别采用阶次粗糙度和阶次幅值表示车轮不圆度。一般认为高阶（大于4阶）多边形

对振动的影响较大，该车车轮高阶多边形呈现8～13阶，结果与振动测试数据分析结果基本一致。

图5为通过时频分析预测轨道磨损位置附近的钢轨损伤情况，轨隙较大，间隔约25 m。左图中钢轨为区域2中一处道岔，该处钢轨轨缝明显，内侧有缺口，深度为约1 mm、长度约60 mm。右圖中钢轨直线段轨面有连续性多处磨损掉块情况，深度达2 mm，这是引起时频图中2430～2460 s时段内宽频高幅值振动的原因。现场调查情况与时频图分析具有一致性。

5 结论

本文基于小波变换时频分析理论采用使用西门子Simcenter TestLab振动控制采集分析系统分析实测的地铁轴箱振动信号成功诊断出车轮多边形和轨道不平顺程度：

（1）未镟轮车辆的车轮多边形主要呈现8～12阶，引起60～85 Hz的谐振，可对车辆设计提供指导；

（2）线路后半段存在轨道接头不平顺和局部轨道磨损；

（3）车轮不圆度测试和线路调查结果与分析结果基本一致，说明了使用小波变换对轴箱振动信号进行时频分析的方法相较于传统车轮和轨道测试手段更为方便可靠；

未来该技术还可以和图像识别技术相结合，实现车轮多边形和轨道不平顺的智能诊断。

参考文献：

[1]Alfi S，Bruni S. Estimation of  long wavelength track irregularities from on board measurement[C]. Derby：Petr Kroca：The 4th IET International Conference on Railway Condition Monitoring，2008：16-22.

[2]Weston P F，Ling C S，Roberts C，et al. Monitoring vertical track irregularity from in-service railway vehicles[J]. Proceeding of the Institution of Mechanical Engineer，Part F： Journal of Rail and Rapid Transi，2007，221（F1）：75-88.

[3]Li D，Meddah A，Hass K，et al. Relating track geometry to vehicle performance using neural network approach[J]. Proceeding of the Institution of Mechanical Engineer，Part F： Journal of Rail and Rapid Transi，2006，220（F3）：273-281.

[4]李成辉. 高低不平顺不利波长及其与车速关系[J]. 西南交通大学学报，1997，32（6）：633-636.

[5]翟婉明，涂贵军，高建敏．地铁线路钢轨焊接区轮轨动力学问题[J]. 振动、测试与诊断，2012，32（5）：701-708.

[6]张富兵，邬平波，吴兴文，等. 高速列车车轮多边形对轴箱的影响分析[J]. 振动、测试与诊断，2018（5）：1063-1068..

[7]彭玉華. 小波变换与工程应用[M]. 北京：科学出版社，2002.

[8]李伟，李言义，张雄飞，等. 地铁车辆车轮多边形的机理分析[J]. 机械工程学报，2013，49（18）：17-22.

[9]陈光雄，金学松，邬平波，等. 车轮多边形磨耗机理的有限元研究[J]. 铁道学报，2011，33（1）：14-18.

[10]胡晓依，任海星，成棣，等.动车组车轮多边形磨耗形成与发展过程仿真研究[J]. 中国铁道科学，2021，42（2）：107-115.

收稿日期：2023-01-09

基金项目：湖南省科技创新计划《新一代轨道交通高效驱动系统技术》（2022GK1060）

作者简介：孙亮（1993－），男，江苏扬州人，工学硕士，工程师，主要研究方向为车辆动力学和机械振动，E-mail：418510780@qq.com。