无中生有 有迹可循
何萍 蔡德清

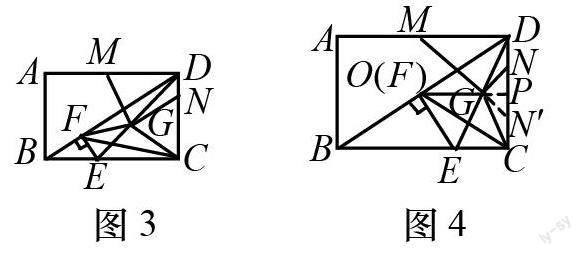
古有女娲补天,今有几何补线.自进入平面几何学习以来,常需面对辅助线解决几何问题的情形.然而,如何构造辅助线却成为解决几何问题的绊脚石,考生时常闻风丧胆,迟迟怯于下笔.事实上,辅助线的构造,建立在考生对几何知识深刻理解、熟练掌握、灵活应用的基础上,并非毫无章法可言.
1 几何常遇拦路虎,百思勤练苦尝试
路径最值问题是一类具有现实意义的几何问题,体现数学在生活中的应用价值.其中,“将军饮马”模型是路径最短问题中最具代表性的典型题型之一,古今中外不乏数学大家深入研究,具有较高的研究价值.寻找最值的过程中,需要尝试在所有可能的结果中觅得“最大”或“最小”值,而此时,对学生而言,却是构造辅助线题型中最高级别难度的问题,考查学生的几何直观感知能力,逻辑推理能力,抽象图形能力,综合分析、解决问题能力,渗透分类讨论思想,极限思想等.
解决这类平面几何问题的过程中,考生需不断构造辅助线,反复推敲,方能找到最值的路径.如若非要套用模型,固化思维,那么将是山穷水尽,而若能灵活变通,则必定能够柳暗花明.因此,理解几何题目中条件里字里行间隐含的内在本质,抽象提取图中的关键要素,动手操作,尝试不同辅助线作法,结合逻辑推理能力,经过反复有机训练,提炼总结归纳几何题解题方法与技巧,则可游刃有余完成几何证明、求解等难题.
2 似曾相识却无解,透过题目析本质
“将军饮马”模型作为大型测试的常客,中考、质检等不乏其身影,笔者以此模型为例剖析辅助线的来龙去脉.涉及辅助线的几何题考法较为灵活,但“将军饮马”模型的考查常常按部就班置于多姿多彩的几何背景中,通过抽象出“一线+两同側点”的几何模型,借助轴对称的几何变换,利用垂直平分线的性质,结合“两点之间线段最短”的基本事实,在已知的“定线”上即可寻得最值点.
2.1 由最值构造对称轴
数学问题的命制最忌熟悉的套路反复出现,必将学生的思维限制在框框条条之中.因此,越是经典的题型,越需要创新的呈现,方能开阔眼界,挖掘潜能,拓展思维.于是,2021年莆田市八年级市质检24题横空出世,本道题的命制反其道而行,不再出现“将军饮马”模型中的那条河,那么该如何寻找消失的河呢?本题前两问是常规的将军饮马问题,笔者不作讨论,仅对第三问进行剖析.
但有别于常规题型,对考生而言,似乎看不到“将军饮马”的影子,陷入困局,关键问题在于“河”隐身了,仿佛失去了依靠而导致无从下手.此时应回归问题本质,转换常规思维,搜索已有知识,类比联想,构造恰到好处的辅助线,这也是本题的精妙独特之处.“将军饮马”模型的内在核心是对称性,而本题的亮点也是难点在于对称轴成为最终的求解目标,而不再是辅助工具.此时需要利用对称不变性,作出点O或点B的对称点,逐步逆向推导,借助构造辅助线补全图形,构建将军饮马模型,便可豁然开朗.
与此同时,本题置于尺规作图的背景中,无形当中命制的创新性又提升一个层次,对考生提出更高的要求,更能展现考生的数学素养.显然,本题解决过程需要不断大胆尝试,巧妙构造辅助线,寻找那条失踪的“河”.回首本题,隐身的“河”即为对称轴,遵循对称性原则,抓住对称变换的变与不变,作出对应点,从而便可按部就班解决问题.
从答题情况看,此题失分除了“将军饮马”模型的应用不够熟练以外,最主要原因是几何思维不够活跃、联想能力较弱导致考生无从下手,不敢轻易动笔尝试.万丈高楼始于纸上,要建筑摩天大厦,要先设计宏伟蓝图,当然设计几何蓝图的依据便是对几何知识的熟练掌握,对几何的核心本质要了然于胸.同时,最为核心的关键点在勇于动笔尝试,敢于构造辅助线,要有试错的耐心、纠错的决心.数学是思维的科学,而几何题需要将思维通过动笔直观展现出来.在思维呈现的过程中,常常需要借助辅助线,使得几何大厦更加牢固,此时便可构造出精彩绝伦的模型.
正如本道题,考生若能将题中简洁的语言表述翻译出较为直接明了的条件要求,进而转化为常见的问题,化新知为旧知,将熟练的几何模型进行逆向迁移,动笔构造辅助线.也许辅助线无法一步到位,但在无数次的尝试甚至错误中,能够有所启发、反思、领悟,从而解题过程便呼之欲出.
2.2 构造对称轴求最值
无独有偶,2021年莆田市九年级市质检24题命制了看似相同却也不同的题型.
原题呈现 如图3,矩形ABCD中,AB=4,BC=8,点E为BC边上的动点,连接DE.过点E作EF⊥BD于点F,点G为DE的中点,连接CF,CG,GF.点M,N分别在ADCD,上,且DM=9/2,DN=1,连接GM,GN,当GM+GN取最小值时,求S的值.
感悟启思 本题第二问的第2小题,目标定位在求GM和GN的和的最小值,即路径最短问题,识别出具体问题背后的一般性后,结合条件,从复杂的图形中,抽象出几何模型,转化为熟悉的“将军饮马”模型.此时,遇到与上例同样的问题,模型虽已联想到,但条件却与常见问题截然不同,此时,将军饮马中的“河”又隐身了.
通过观察图形,思考探究,分析题意,点E为主动点在线段CB上运动,DE随之运动,G为DE中点,得出从动点G在ΔBCD的中位线OP上运动,此时,最关键的辅助线OP便跃然纸上.取得将军饮马模型的钥匙后,便可打开最值的大门,借助作点N关于OP的对称点N′,如图4,线段MN′的长即为GM+GN的最小值.
涉及最值问题,渗透极限思想,需针对具体问题展开更为全面的分析,特别地,与动态几何题的相互交融,使得数形结合展现得更加丰富、饱满.本题的关键点便是辅助线OP的寻觅,全方位考查考生几何直观、动态几何抽象、逻辑推理等关键能力的掌握水平.看似辅助线无从下手,而实际上OP的轨迹通过逐步推导构造.实际上,无论多繁杂的题目,都可借助波利亚的四个解题步骤,抽丝剥茧,层层递进解决问题,几何题尤为如此.当然,几何题有独特精妙之处,便是至关重要的辅助线.
综上所述,例1已知定性的最值点,由点求作对称轴,需紧抓对称性,分析对称变换的变与不变,循序渐进思考,活跃逆向思维,类比路径最短问题的求值,联想到“将军饮马”模型,巧妙构造辅助线,由最值点反推求作出直线,即对称轴;例2通过构造对称轴,定量求解最值,由题中线索构造辅助线,进而借助“将军饮马”模型,正面求解最值问题.两道例题完美展现双向考查同一个知识点的策略,灵活置换条件、结论,但隐身的对称轴保密性较强,通过辅助线的构造外显考查.因此,辅助线的构造是否灵活便可综合考查考生的几何知识掌握水平.
总而言之,平面几何问题中,尽管是同一个模型,但是切换为正、反面不同角度,则需创造性又有理有据构造匹配不同题型的恰当的辅助线,要点在于因题而异,由题定线.
3 百般题型皆如此,探本求源构辅助
平面几何题千千万,切忌题海里漫无目的遨游,解几何题的旅程尤其需要明确的目标.几何题目设置的问题便是航行的方向,几何的定义、公理、定理等知识决定航行的动力,而辅助线就是旅程的航线,尤为重要.航线众多,构造方法多样,需根据自身具备的几何知识,结合题中条件合情推理、演绎推理,选择正确的方向.一旦偏航,掌舵者也就是考生,便如无头苍蝇,在几何图形前束手无策,胡乱打转,随意构造辅助线,无法攻克几何问题.正所谓“兵马未动,粮草先行”,要想应对航行中遇到的各类难题,考生需储备充足的几何知识,武装充满几何思维的大脑,掌握丰富的解题经验.
幾何问题中的辅助线,皆有因果.以题中出现“中点”条件为例,则应联想到作中位线、直角三角形斜边上的中线、倍长中线,亦或是利用等腰三角形三线合一的性质、全等三角形的判定、三大几何变换的性质构造图形.与此同时,对于几何题中出现的线索要擅于挖掘,结合已掌握的知识,大胆尝试构造辅助线.解题方法、技巧、思维在脑中,但是辅助线在笔下,只有将二者有机结合,才可攻破几何难题.初中阶段的几何综合题,往往是包含千变万化的辅助线作法的平面几何题,全面考查几何直观想象、逻辑推理、数学建模、数学抽象等核心素养,深挖分类讨论、数形结合、转化化归等数学思想,体现分析问题、解决问题的关键能力,具有较高的命题价值,值得引起关注.
无论是何种题型,教学中切不可将模型放在首位,生搬硬套,那必定会本末倒置,限制思维的发展,而应当重视学生高阶、多向思维的发展,甚至遇到难题时更要不走寻常路,逆向、反向思考,或许能有顿悟之感.模型思想的渗透,应当在于引导学生灵活掌握各个知识点,并能够独立自主探究,主动构建恰当的模型,模型应为生所用,而非将模型奉为学习法宝.只有透过问题的表面,挖掘内在的本质,才能构造相得益彰的辅助线,搭线牵桥,配合严谨的逻辑推理,高效解决问题.明面上,辅助线貌似无中生有,事实上,暗含条件中、图形中、问题中,有迹可循,从而构造打开解题大门的重要辅助线.而这,恰是几何,更是数学的魅力.
女娲补天也许只是传说,美丽而神秘,然而,辅助线却是真实存在,是每位中学生所必须面临的一道坎,其实它也是神奇而美妙的.面对几何问题感到困惑迷茫时,可能只是“不识庐山真面目,只缘身在此山中”,尚未从新问题联想到已知、已求、已证中.此时,发散活跃思维,不走寻常路,不落套路,或倒行逆解,或顺势而为,或另辟蹊径,构造恰如其分的辅助线,以期达到解题的目的.

