基于知识空间理论的八年级学生代数关键学习路径

姚必

1 引言

《义务教育数学课程标准（2011版）》指出：函数是从具体情境中抽象出数学符号的过程，是探索具体问题中数量关系和变化规律的重要模型[1]．其中，“一次函数图象”不仅是函数知识的入门基础，还是解决其它实际问题的重要手段[2]．通过“一次函数图象”的学习，学生能够在平面直角坐标系中画出一次函数的图象，并且根据图象了解一次函数的性质，从而掌握数形结合的数学思想[3～4]．知识空间理论（简称KST）为基于计算机网络系统的知识和学习评估的发展提供了一个有效的数学理论框架，能有效地诊断学生对于某一个学习领域的掌握情况[5]．知识空间理论在国外已经广泛应用于数学学习的认知诊断中，但是在国内，与该理论相关的实证研究仅仅局限于化学教学实践[6～7]．因此，本研究应用知识空间理论对八年级学生的“一次函数图象”的学习情况进行具体描述和深入分析．

2 知识空间理论

Doignon和Falmagne认为：问题与对应的知识之间存在联系[8]．如果学习者能够解答某个问题，那么该学习者拥有这个问题相应的知识[8]．将某一个领域看成相关问题组成的集合Q[8]．问题有高低层次之分，如果作答者能解决高层次的问题，那么也一定可以解决相应的低层次问题[8]．将各个层次问题之间的关系称为推测关系（surmise relation），符合推测关系的集合称为知识状态（knowledge state）[8]．所有知识状态加上空集和集合Q组成的集合称为知识结构（knowledge structure），记为（）Qκ，[8]．若（）Qκ，满足对并运算的封闭性，即知识状态的任意并还是知识状态，则（）Qκ，称为知识空间（knowledge space）[8]．在知识空间中，我们用箭头表示包含的覆盖关系，如果L是包含知识状态K的极小知识状态，那么存在从知识状态K到知识状态L的箭头，以空集为起始点、全集为终止点，将各个知识状态通过一定的顺序依次连接起来，建立具有层级关系的网络结构[8]．每一个从空集到全集的知识状态组合，形成问题有序增长的组合称为分级[6]．各个分级中，可以找到一条具有最大出现概率的问题有序组合，我们称这个问题的有序组合为关键学习路径[8]．

3 研究方法

3.1 研究对象

本研究选取江苏省苏州市吴江区某中学八年级两个普通班共102名学生进行专题测试．这两个班级学生的数学成绩整体相当．在八年级第二学期进行测试，参与本次测试的学生对于“一次函数图象”的知识点已经进入长时记忆中，测试结果可以较好地体现学生关于该知识点的学习情况．

3.2 研究工具

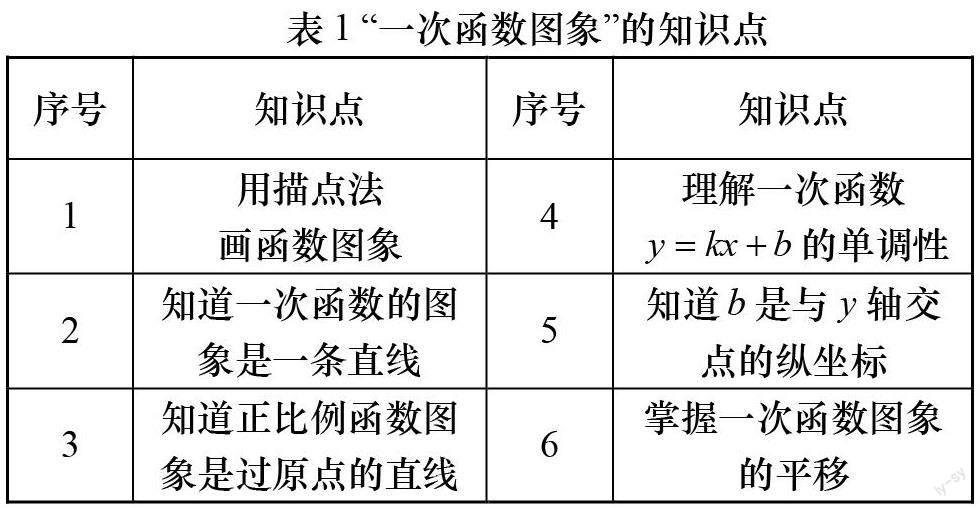
本研究基于《义务教育数学课程标准（2011版）》，使用《义务教育教科书·数学（八年级上）》（江苏凤凰科学技术出版社），先初步筛选测试题，再结合专家型数学教师的建议对测试题进行修改，最后征求专家教授的建议对测试题进行精选．本研究测试卷涉及6个知识点，详见表1．其中，知识点的序号代表了专家预设的学习路径．

3.3 研究流程

在八年级第二学期的第一个月内完成“一次函数图象”的专题测试．测试结束后，笔者回收试卷，批改学生的作答结果和记录学生的答题情况．将学生答对、答错的情况分别记录为1和0，则测试卷上所有问题的解答情况可以转化为一个有序数字组合．该组合就是学生的反应模式．例如，某位学生仅答对了第1、2、3、5题，那么该学生的反应模式为[111010]……

3.4 数据处理

参考知识空间理论，本研究使用python语言自主设计相关算法程序，并且将所有的反应模式和相应的人数作为原始数据．本研究的算法程序需要经历两个过程．首先，统计每一个反应模式所对应学生的人数，并且获取相应的知识状态；同时，根据问题之间的推测关系，添加必要的工作假设（working hypothesis）[9]，从而建立完整的知识空间．通过可视化功能，呈现知识空间的示意图．其次，计算反应模式的概率，并且通过概率值确定关键学习路径．在此过程中，基于已有文献[679]，，的研究，该程序设定猜测幸运（lucky guess）和粗心失误（careless error）的概率均为0.1．

4 研究结论

4.1 学生的答题情况

学生总体的平均答对率为45.15%．其中，每一道题的平均答对率详见表2．

由表2可见，第1题的答对率最高．结合表1中对应知识点的说明，可以发现“用描点法画函数图象”这个知识点学生的掌握较为熟练．进一步地，由学生答题情况的质性分析还表明：学生对图象过于依赖，导致学生缺乏函数图象和函数解析式之间转化的能力．同时，第4题的答对率明显较低．根据学生解答过程的分析发现，学生倾向于默认“单调性”为“单调递增”，而往往会忽视“单调递减”这种情况．究其原因，结合对任课教师的深度访谈，是教学中教师通常会以单调递增的函数作为例题和练习题．此外，由表2还可见，第3题的答对率最低．这充分说明对于定点问题，学生的理解和掌握有严重的欠缺．深度分析教材内容，其原因很可能是由于教材中未详细解释和区分“原点”和“定点”的内涵，导致绝大多数学生无法对“正比例函数图象”实施有效的思维拓展．

4.2 学生的关键学习路径

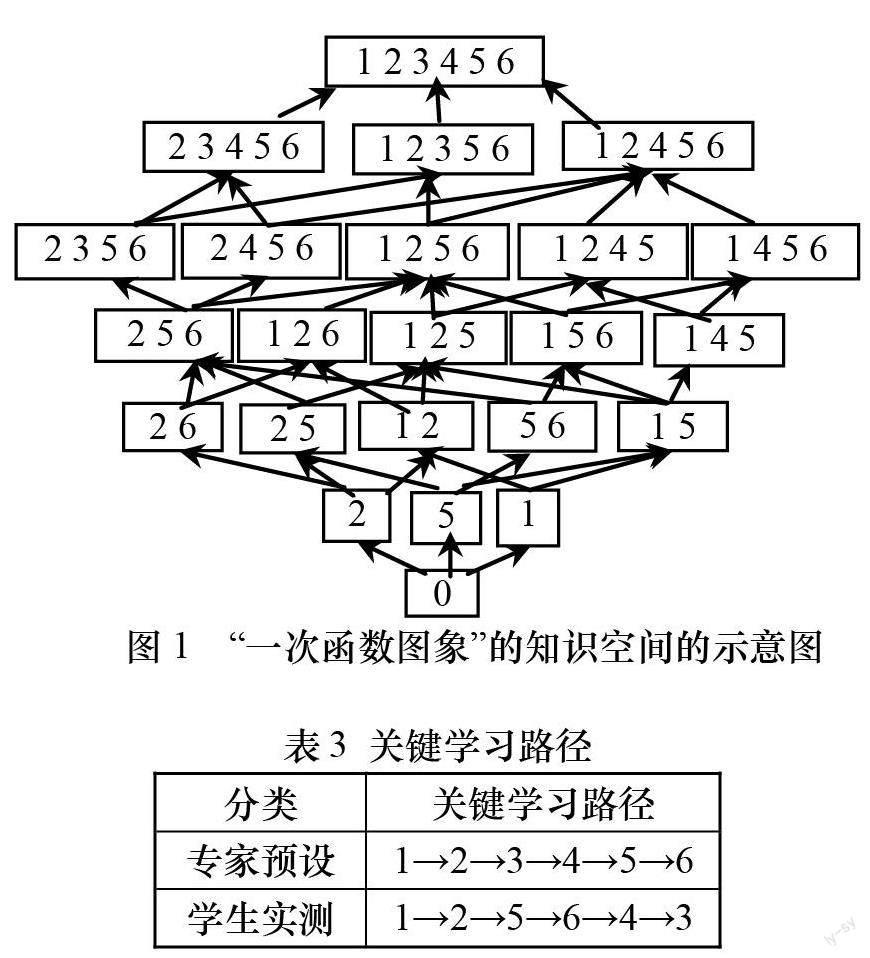
八年级学生关于“一次函数图象”的知识空间的示意图详见图1．关于“一次函数图象”这个知识点，图1显示了知识状态的数量较多，并且知识状态之间的连线也较多．由此可见，八年级学生关于该知识点的知识空间的结构较复杂．通过计算反应模式的整体概率，我们可以得到八年级学生的关键学习路径，如表3所示．

基于学生关键学习路径的分析，可以发现：“描点法”和“一次函数的图象是一条直线”出现的位置处于较前端．这说明八年级学生将上述两个知识作为“一次函数图象”学习的基础．同时，还可以发现：“一次函数的单调性”以及“正比例函数图象过原点”处于学习路径的末端．这说明对于这两个知识点，学生较难理解和掌握．究其原因，可能是因为在数学学习的过程中，只有熟练掌握了数形结合的思想，学生才能將“一次函数图象”和“一次函数解析式”融合起来，从而有效地解决一次函数单调性的相关问题．进一步地，由表3还发现：学生实际的关键学习路径与专家预设的学习路径存在明显的差异．例如，知识点“知道b是与y轴交点的纵坐标”和“掌握一次函数图象的平移”出现在学生实际的关键学习路径的中间位置．

5 结论与建议

5.1 研究结论

以“一次函数图象”为例，本文首次将知识空间理论应用于八年级学生代数关键学习路径的探讨和分析中，从而为数学教育心理学中的代数学习研究提供了一个新的视角．研究结果表明：（1）学生实际的关键学习路径与专家预设的学习路径存在明显的差异；（2）学生知识空间的结构较复杂，同时出现了23个知识状态；（3）学生在一次函数单调性和正比例函数过原点的相关问题上的学习表现有待改善．

韬尔将函数的概念作为数学认知根源，并将函数的概念分为前程序、程序、过程、对象和过程性概念五个层次[10]．基于该理论，本次调研发现：有极少数学生处于前程序阶段，对于画出一次函数图象还一无所知；大多数学生处于程序阶段，解题依赖于固定的操作步骤；只有少数学生处于过程阶段，能够熟练应用函数的输入与输出，不依赖于固定的操作步骤；仅仅有一到两位学生处于对象层次；没有学生能到达过程性概念层次．

5.2 教学建议

基于学生实际的关键学习路径，我们可以提出如下三点教学建议． 第一，教师预设的教学设计和学生实际的学习现状存在差异．教师需要判断对大多数学生来说存在认知障碍的知识点，例如，将“正比例函数过原点”放在关键学习路径的后面，体现出学生尚未熟悉函数不同表征之间的关联，不知道什么时候用哪一种表征比较容易解决问题．尽管大多数学生都知道正比例函数图象过原点，但是用另一种非标准形式去表示正比例函数的时候，学生会无从下手．因此，在后续的教学中，教师需要培养学生识别函数的能力，提升学生从函数的一种表征转化到另一种表征的能力． 第二，对于基础较差的学生，过于依賴一次函数的表达式，而难以从图象上获取相关信息．教师应该在教学过程中，将用图象表示函数的方法贯穿整个一次函数的教学过程中，不断提高学生用图象直观表示函数的性质以及解释由图象表示的函数相关信息的能力．同时，教师也可以利用相关计算机软件来辅助教学，比如几何画板，将函数运动、变换等特点直观化．

第三，考虑到同一所学校近几年的生源比较相似，在下一学年的教学中，对于“一次函数图象”这节课，教师要重点关注学生对于一次函数单调性和定点问题的掌握程度，并在教学后通过专题训练等方式加以巩固．同时，学生实际的关键学习路径可以为教师的新课教学提供一定的参考．从学生实际的关键学习路径中可以看出，学生数学思维水平仍处于初级阶段，需要教师在新课教学中重点突出函数解析式与图象之间的关联与转换．

5.3 研究展望

本研究以“一次函数图象”为例，深入探讨和具体分析了八年级学生的知识空间结构．在未来的研究中，对于不同的数学学习内容和不同学习阶段的学生，还可以应用知识空间理论进行深入的探讨和分析，从而丰富已有的研究成果，进而为数学学习过程提供更多的实践依据和理论支撑．