桥头搭板与路基路面结构一体化研究
李 洁
(济宁市鸿翔公路勘察设计研究院有限公司,山东 济宁 272000)
1 桥头搭板设计的理论
1.1 有限元分析理论的核心内容
有限元分析理论的核心内容是七个步骤:一是将构件的结构离散化,形成规格一致的有限单元网格;二是通过计算所有单元网格的刚度矩阵从而得到结构构件总的刚度矩阵;三是利用各个有限单元形成关于单元节点的荷载向量;四是根据结构构件所处的实地环境引入外部约束条件,建立线性代数方程组;五是依据函数关系式或者数学计算软件求解线性数学方程组;六是开展节点的位移(即横向或者是纵向的压缩变形量)计算;七是核算相应压缩变形量境况下对应的单元应力[3]。
1.2 桥头搭板设计中的有限元分析理论
首先将桥头搭板看作一块板式结构构件(含枕梁部分),再把桥头搭板构件与天然路基、填土路堤一起看作是相同性质且质地均匀的同一材料,即某一弹性体。从而将某一同质均质弹性体看作是桥头搭板与路基路面结构一体化的外在表现。
1.3 同质均质弹性体的有限元微分方程
在使用有限元分析理论对桥头搭板及路基路面一体化进行分析时,先将同质均质弹性体划分为无数个规格大小一致的矩形单元。如图1所示,某一矩形单元长度2a,宽度2b,厚度为t,以该矩形单元的中心点o作为原点建立平面x,y坐标系,则矩形单元内任一无量纲坐标(ζ,η)=(x/a,y/b)[4]。
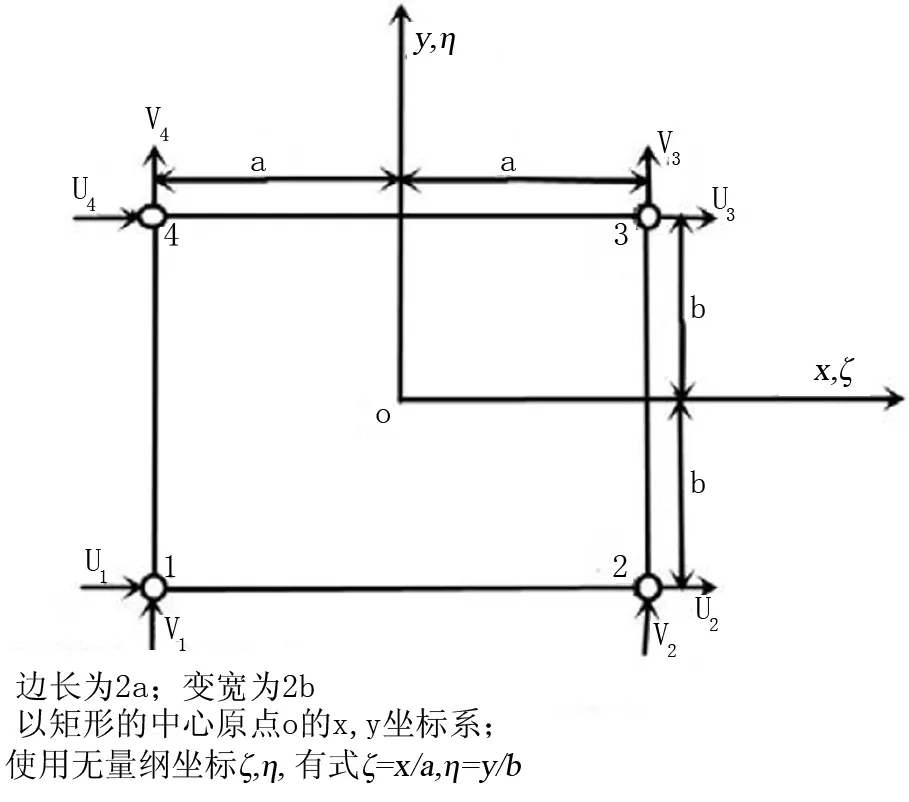
图1 同质均质弹性体矩形单元
若将图1所示矩形单元的四个角点看作节点i,那么节点i的无量纲坐标(ζi,ηi)分别为(1,1)、(1,-1)、(-1,-1)、(-1,1),由此可以推算出矩形单元内某一节点的单位移向量如式(1)所示,矩形单元任意一点的位移采用单元节点的位移进行表示,可用式(2)表示。
ac=[u1v1u2v2u3v3u4v4]T
(1)
式中:a为同质均匀弹性体矩形单元的1/2长度;c为同质均匀弹性体矩形单元内某一节点;ac为同质均匀弹性体矩形单元内某一节点c的位移向量;u1为同质均匀弹性体矩形单元顶点1受到的横向约束;v1为同质均匀弹性体矩形单元某一顶点1受到的纵向约束;u2为同质均匀弹性体矩形单元顶点2受到的横向约束;v2为同质均匀弹性体矩形单元某一顶点2受到的纵向约束;u3为同质均匀弹性体矩形单元顶点3受到的横向约束;v3为同质均匀弹性体矩形单元某一顶点3受到的纵向约束;u4为同质均匀弹性体矩形单元顶点4受到的横向约束;v4为同质均匀弹性体矩形单元某一顶点4受到的纵向约束;T表示约束周期[5]。
U=Nac
(2)
式中:U为同质均匀弹性体位移向量;N为同质均匀弹性体矩形单元矩阵。
在式(2)中,矩阵N值的计算如式(3)所示,在矩阵N中,向量Ni的计算如式(4)所示,且Ni具有如式(5)所示的特征。
(3)
(4)
(5)
式中:Ni为同质均匀弹性体矩形单元向量;ζi为同质均匀弹性体矩形单元节点i的无量纲横坐标;ηi为同质均匀弹性体矩形单元节点i的无量纲纵坐标;ζ为无量纲横坐标修正系数;η为无量纲纵坐标修正系数。
1.4 桥头搭板的有限元理论
基于前文中同质均质弹性体的有限元微分方程,可以推知,当把桥头搭板和路基路面作同质均匀弹性体看待时,搭板、路基和路面之间必然存在与外力相关联的因素。假定桥头搭板与路基路面之间的外力作用F=(Nx,Ny,Nz)T,桥头搭板与路基路面在外力作用下处于稳定状态的位移为U=(Ux,Uy,Uz)T,当此位移值是在安全的位移范围内,即表明桥头搭板与路基路面之间的结构一体化效果较好,桥头搭板与路基路面组成的整体,沉降稳定,无安全隐患[6]。
虽然有限元分析理论在我国多个工程领域已经得到了应用实践,但是在高速公路桥头搭板与路基路面的一体化设计领域,其应用探索还相对较少,因此基于有限元分析理论开展高速公路桥头搭板与路基路面的一体化设计探究,尤其是针对桥头搭板与路基、路堤临界衔接区域的一体化进行设计探究,对于今后一段时期内就提升桥头搭板的使用效能,保障高速公路上车辆的行驶安全而言是非常有益的。
2 桥头搭板与路基路面一体化设计案例分析
2.1 云贵高速武定桥工程概况
云贵高速武定桥桥梁设计长度1 800 m,宽度24 m,双向四车道。该高速公路桥梁有一段长度LK=750 m的距离范围属于脱空区,桥头搭板与桥梁的一体化设计长度为L,桥头搭板长度L搭=L-LK,以桥头搭板方向为横向X方向,以垂直于桥头搭板的方向为竖向Y0方向,可以看出云贵高速武定桥的桥梁一端受简支桥台约束,另一端桥头搭板置于路堤上受路堤支承。以桥头搭板与路堤的接触点为临界衔接接触中点,临界衔接接触中点左右0.7 m范围内(总长度1.4 m范围内)的均值荷载设计值为70 kN。
2.2 云贵高速武定桥桥头搭板设计类型的初步确定
在我国,高速公路桥头搭板的设计类型主要有单段式搭板、多段式搭板、可抬升式搭板三种类型。单段式搭板属于典型的桥头一端置于台背部位,搭板一端置于台背墙顶的两端约束类型,和云贵高速武定桥的约束类型最为相似,但是单段式搭板的长度一般较小;多段式搭板通常适用于长度在10 m以上的桥头搭板设计;可抬升式搭板虽然构造最为简单,但是对于路基的强度要求较高,一般可抬升式搭板需要使用高强度混凝土换填至少30 cm厚的天然路基或者填筑路堤作为台座式千斤顶的基础。基于项目投资成本控制的考虑,云贵高速武定桥项目的设计人员初步确定选择单段式搭板或者多段式搭板作为桥头搭板的设计类型。
2.3 云贵高速武定桥桥头搭板长度的设计与搭板类型的确定
根据前文可知,云贵高速武定桥桥头搭板与桥梁的一体化设计长度为L,桥头搭板长度L搭=L-LK,按照现有最新版本的《公路工程技术标准》和《公路路线设计规范》要求,桥头搭板的长度L搭需要大于路堤不均匀沉降段的长度,而且路堤不均匀沉降段的纵向坡度变化率需要控制在4‰到6‰以内。由此云贵高速武定桥项目的设计人员依照《公路工程技术标准》和《公路路线设计规范》中的搭板长度L搭计算公式,如式(6)所示,进行桥头搭板长度L搭的设计值确定。
L搭=△h/△i
(6)
式中:L搭为桥头搭板长度,cm;△h为桥台与填筑路堤之间的不均匀成降值,cm;△i为路堤不均匀沉降段的纵向坡度变化率,%。按照《公路工程技术标准》和《公路路线设计规范》的要求,△h≤10 cm;《公路工程技术标准》和《公路路线设计规范》规定4‰≤△i≤6‰。
根据对云贵高速武定桥附近其他高速桥梁路基、路堤的长年不均匀沉降监测与记录,发现云贵高速武定桥周边最近的兴源高速桥路基、路堤的纵向坡度最小沉降为4.5‰,最大沉降为5.8‰,为了充分保障桥头搭板的长度设计安全,保守起见,项目设计人员以△h=10 cm作为云贵高速武定桥桥台与填筑路堤之间的不均匀沉降参考值,以△i=5.8‰作为云贵高速武定桥的纵向沉降坡度设计参考值。由此根据式(6)计算得出云贵高速武定桥的桥头搭板设计长度L搭=△h/△i=10 cm/5.8%≈1 724.14 cm≈17.24 m>10m
前文中提到云贵高速武定桥项目设计人员初步决定选择单段式搭板或者多段式搭板作为桥头搭板的设计类型,根据上面的计算结果可以看出,云贵高速武定桥的桥头搭板设计长度约为17.24 m>10 m,故应选择多段式桥头搭板作为云贵高速武定桥桥头搭板的设计类型。
基于上述设计分析和计算,可以得出云贵高速武定桥的桥梁一段长度LK=750 m,桥头搭板设计长度L搭≈17.24 m,那么云贵高速武定桥与桥头搭板的一体化设计长度为L=LK+L搭≈767.24 m,且为多段式桥头搭板。
2.4 基于ANSYS模型分析桥头搭板与路基路面的一体化
ANSYS软件是开展有限元数学建模分析运用的常用软件,通过针对云贵高速武定桥桥头搭板与路基路面之间结构一体化的ANSYS软件模型分析,验证前文中的理论设计成果。
在ANSYS软件中,输入桥梁与桥头搭板的一体化长度近似值767.24 m,该桥的桥头搭板厚度参考云贵高速武定桥附近兴源桥的桥头搭板厚度与宽度,厚度取值h=0.4 m,宽度取值b=3.8 m,经测算该桥头搭板成品钢筋混凝土构件的弹性模量为29 800 MPa。桥头搭板与路基路面临界衔接接触中点左、右0.7 m范围(总长度1.4 m范围内)的均值荷载设计值为70 kN,经试验测得路基土体弹性模量1 600 MPa,路面土体弹性模量1 700 MPa。将此结合体桥头搭板与路基路面临界衔接接触中点左右0.7 m范围(总长度1.4 m范围内)的临界衔接区段通过ANSYS软件分割为尽可能小的规格一致矩形单元。
接着使用ANSYS软件根据公式(1)至公式(6)就桥头搭板与路基路面临界衔接区段0.7 m范围(总长度1.4 m范围内)在外力均质荷载70 kN的作用下,处于稳定状态时的位移进行计算,得出的计算结果表1所示。

表1 同质均匀弹性体稳定状态时的位移
经过有关测算,在表1所示稳定状态下的变形位移量,对于发生桥头跳车现象的可能性很低,遂而验证了云贵高速武定桥桥头搭板与临界衔接区域路基路面一体化设计的使用安全性。此外我们也可以看出,在当前我国《公路工程技术标准》和《公路路线设计规范》的指导下,桥头搭板的设计类型和设计长度虽然受到了设计区域路基、路堤不均匀成降值和纵向坡度变化率的严格限制,但是使用有限元分析理论对桥头搭板与路基路面临界衔接区域的计算分析显示,我国现行的《公路工程技术标准》和《公路路线设计规范》对于保障桥头搭板的设计安全而言是起到了较好的指导作用的。
3 结 语
梳理有限元分析理论的核心内容,从同质均质弹性体的有限元微分方程角度明晰和掌握桥头搭板设计中的有限元分析理论,以云贵高速武定桥桥头搭板设计类型的初步确定、桥头搭板的长度设计和桥头搭板类型的进一步确定以及利用ANSYS软件对云贵高速武定桥桥梁与桥头搭板的一体化长度开展路基路面一体化位移建模分析。根据模型数值分析结果可以看出,云贵高速武定桥桥头搭板与路基路面临界衔接区段在外力均质荷载70 kN的作用下,距离衔接中点0.3 m处、0.5 m处、0.7 m处的稳定状态位移量分别为0.41、0.38、0.32 mm,其位移量非常小,发生桥头跳车现象的可能性很低。从而得出云贵高速武定桥的桥梁桥头搭板与路基路面一体化设计符合有限元分析理论标准与最新《公路工程技术标准》和《公路路线设计规范》的结论。

