一种基于体素网格的三维点云均匀降采样方法
肖正涛,高 健,吴东庆,张揽宇
(1.广东工业大学省部共建精密电子制造技术与装备国家重点实验室,广东广州 510006;2.广东工贸职业技术学院机电工程学院,广东广州 510510;3.仲恺农业工程学院计算科学学院,广东广州 510220)
1 引言
随着三维激光扫描技术的快速发展和普及,三维点云的获取变得越来越容易。由于三维激光扫描技术具有非接触、高效率、高精度等优点,已被广泛应用在自动化加工生产线、虚拟现实、无人驾驶汽车等领域。由于实际得到的三维点云数据往往包含有大量的冗余数据,在使用点云数据前通常要进行降采样(Downs⁃Ampling[1])处理,以提升点云的最终处理效率和效果。
降采样,也称下采样,简而言之就是对点云进行精简[2−3]。点云降采样的方法有很多,通常分为不考虑点云细节特征和考虑点云细节特征两大类。不考虑点云细节特征的降采样方法有体素网格(Voxel Grid[4])、系统采样(Systematic Sampling[5])、随机采样(Random Sampling[6])、最远点采样(Farthest Point Sampling[7])等。考虑点云细节特征的算法一般会将点云的法向、曲率、是否位于边缘等信息结合在内。文献[8]提出了一种基于栅格动态划分的点云精简方法,对不同的区域采取不同精简策略,该方法能较好地保持模型的细微特征。文献[9]提出了一种能够保留边缘点的点云简化算法,通过八叉树建立k邻域,以法向量为依据检测并保留边缘特征点,该算法保留的边缘点大部分为模型的尖锐点。文献[10]提出了一种自适应下采样深度学习网络,该方法能根据应用、任务和训练数据的不同,减少无序点云中的点数,同时保留重要点。文献[11]提出了一种基于曲率泊松碟采样的散乱点云精简方法,该方法通过计算点云的曲率特征将点云划分为平坦区域和特征区域,然后对不同的区域使用不同的降采样策略,使得平坦区域能够均匀精简的同时最大化地保留点云的细节特征。这些不同的降采样方法通常有各自适合的应用场景。
体素网格法是一种常用的降采样方法。该方法先对三维点云建立轴向包围盒(Axis−Aligned Bounding Box,简称AABB[12]),然后沿各个坐标轴方向将包围盒分成n等份,接着计算每一个体素中所有点的重心,并将其作为该体素的采样值。体素网格法计算效率高,当轴向包围盒在x,y,z轴三个方向的边长相差不是太过悬殊的情况下,得到的采样点分布均匀,因而该方法被广泛使用。
体素网格法存在着一个不足之处:当点云的轴向包围盒在x,y,z轴三个方向的边长相差较大的时候,体素网格法得到的点云就变得不均匀,在长边方向点的分布较稀,在短边方向点的分布变得密集。不均匀点云会影响点云的法向和曲率计算,进而影响点云的后续处理,如配准、特征计算等的效果。因而,确保降采样后的点云在空间分布均匀是一项非常重要的工作。
针对传统体素网格法存在的不足,提出了一种新的体素网格法。该方法将点云轴向包围盒沿x,y,z轴三个方向的边分成不同的份数,使得每一个体素近似是正方体而不是与包围盒相似的长方体,然后计算每一个体素内所有点的重心,并将其作为该体素的采样值。这样,无论轴向包围盒x,y,z轴三个方向的边长是否相差悬殊,新的体素网格降采样方法皆可得到均匀分布的降采样点云。
2 一种新的体素网格法
当点云轴向包围盒在x,y,z轴三个方向的边长相差不是太过悬殊的情况下,传统体素网格法表现优异,不仅计算效率高,而且得到的采样点在空间分布也非常均匀。但当点云轴向包围盒在x,y,z轴三个方向的边长相差非常悬殊的时候,由于x,y,z轴三个方向的边都分成同样的份数,每一个体素皆是一个与包围盒相似的小长方体,因而每一个体素的边长同样也会相差悬殊,最终会导致包围盒最短边所在方向的采样点分布比最长边所在方向的点分布要密集得多,也即采样点在空间分布不均匀。
针对传统体素网格法存在的问题,提出了一种新的体素网格降采样方法。该方法将点云轴向包围盒x,y,z轴三个方向的边分成不同的份数,使得每一个体素是正方体而不是与包围盒相似的长方体。假设正方体体素的边长是dLen,则点云轴向包围盒x,y,z轴三个方向的边分成的份数如下:
式中:Lx、Ly、Lz—轴向包围盒沿x,y,z轴方向的边长;nx、ny、nz—轴向包围盒x,y,z轴三个方向的边分成的份数;round—四舍五入运算。
从公式可知,最终得到的每一个体素近似是一个正方体,如图1(a)所示。任意点所在体素的三维索引( )

图1 一种新的体素网格降采样方法Fig.1 A Novel Voxel Grid Downsampling Method
i,j,k的计算公式,如式(2)所示。
式中:dx、dy、dz—点到包围盒左侧面、前表面和下表面的距离;
trunc—截断取整;其余符号表示的意义与公式中的相同。
将所有体素的三维索引转换为一维索引,如图1(b)所示。如果按照先x轴方向,然后y轴方向,最后z轴方向的顺序,从三维索引到一维索引的转换公式如下:
式中:idx—体素的一维索引,i∈[0,nx],j∈[0,ny],k∈[0,nz]。
这样,每一个三维索引(i,j,k) 就唯一对应着一个一维索引idx。每一个一维索引idx也同样唯一对应着一个三维索引(i,j,k),从公式可推知一维索引到三维索引的计算公式如下:
式(3)和式(4)建立起了体素三维索引与体素一维索引的一一对应关系。新的体素网格降采样方法的算法过程是:首先对点云建立轴向包围盒,然后以某一个等分距离对包围盒沿x,y,z轴三个方向的边进行等分,使得每一个体素近似为一个正方体,然后计算每一个体素内所有点的重心,并将其作为该体素的采样值。整个算法,如算法1所示。
算法1 一种新的体素网格下采样方法
Algorithm.1 A Novel Voxel Grid Downsampling Method
3 实验
3.1 实验环境和实验点云
实验点云数据是用CREAFORM HandySCAN 700手持式三维激光扫描仪获得,以OpenCV和PCL(Point Cloud Library)为计算平台,计算机配置是Intel 酷睿I5−7200U,12GB内存。分别使用传统的体素网格降采样方法和新的体素网格降采样方法对三维点云进行降采样,从降采样的直观效果和数据分析对两种方法进行了比较和讨论。实验用的点云,如图2所示。从两个场景扫描获得两个点云,两个场景中的物体主要是机加工零件。图2(a)中的零件包含有凸起和凹陷的平面、阶梯圆柱面、球冠面,还包含有凸起的文字和复杂曲面,其对应的点云,如图2(c)所示。图2(b)中有3个散乱放置的L形零件,其对应的点云,如图2(d)所示。图2(c)、图2(d)在展示各个点云的同时,也展示出了各个点云的轴向包围盒。表1展示了两个实验点云各自包含的点数和尺寸,其中尺寸是指各个点云轴向包围盒在x,y,z轴三个方向的边长。结合图2(c)、图2(d)和表1,可知两个点云轴向包围盒的边长比例皆不相同,其中点云二的包围盒在z轴方向的边长与在x,y轴方向的边长差异非常悬殊。

表1 实验点云和轴向包围盒边长(mm)Tab.1 Experimental Point Clouds and the Side Length of the Axis-Aligned Bounding Box(mm)

图2 实验点云Fig.2 Experimental Point Clouds

图3 体素总数和计算时间Fig.3 Total Voxels and Computation Time
3.2 实验结果和分析
使用新方法,等分距离取10mm和15mm时,各个点云轴向包围盒在x,y,z轴方向等分的份数和降采样后的点数,如表2所示。结合表1、表2可知,由于各个点云轴向包围盒在x,y,z轴方向的边长各不相等,因而用新方法对点云进行体素划分时,x,y,z方向的等分数也各不相同。
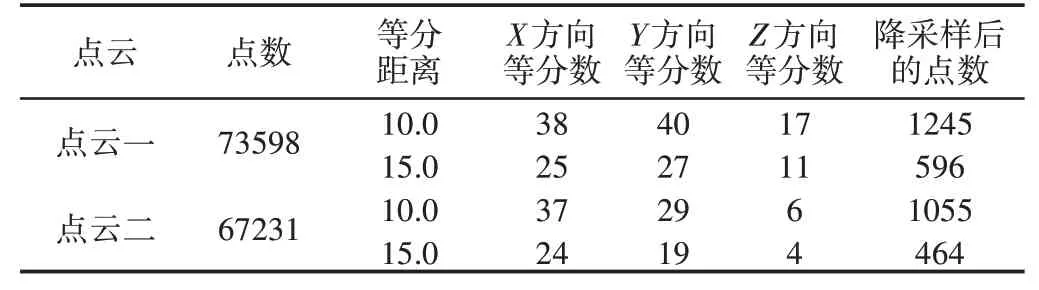
表2 新方法降采样的结果(mm)Tab.2 Downsampling Results of the Proposed Method(mm)
为了便于比较新方法和传统体素网格方法的降采样效果,使用传统体素网格降采样方法,选取不同的等分数对点云进行降采样,记录各个点云不同等分数对应的降采样后的点数,如表3所示。在表3中,无论等分数为多少,降采样后的点数量与表2中新方法降采样后的点数量都不相同。因而,我们从表3中选取降采样后的点数量与表2中降采样后的点数量接近的值,并在表3中加粗显示。同时,将表3中的这些数据摘抄出来,结合表2,并加上每种降采样方法所用的计算时间,如表4所示。

表3 不同等分数对应的降采样后的点数Tab.3 The Number of Points After Downsampling Corresponding to Different Subdivision

表4 体素网格法和新方法降采样的结果对比,长度单位mm,时间单位sTab.4 Comparison of the Results of the Voxe Grid and Proposed Methods,Length Unit in mm and Time Unit in Seconds
图4展示了用体素网格和新方法降采样后的点在原始点云中的实际效果,其中降采样后的点用粗点显示,原始点云用细点显示。从图4 中可见,对点云一,在降采样点数量接近的情况下,直观上看,体素网格方法和新方法降采样效果的差异不明显;对点云二来说,在降采样点数量接近的情况下,体素网格方法和新方法降采样效果有非常明显的差异。差异主要体现在三个L形的零件在z轴方向的采样点分布,体素网格方法得到的采样点在z轴方向分布非常密集,而新方法得到的采样点在z轴方向分布非常均匀。

图4 体素网格法和新方法降采样后的实际效果对比Fig.4 Comparison of the Actual Effects of the Voxel Grid and Proposed Methods
计算降采样后的点云各个点到其最近点的距离,并绘制相应的频数分布图,如图5所示。图5中水平轴表示各点间的最近距离值,纵轴表示距离值在某个区间内的点的数量。为了便于比较分析,当降采样点云的点数接近时,对应的水平轴和纵轴的最大刻度和间隔皆取为相同。在图5(a)、图5(b)、图5(e)、图5(f)中,也即点云一,当降采样点云的点数接近时,靠近水平刻度0的几个频数分布无明显差异,且频数都比较小,这表明体素网格方法和新方法得到的采样点都没有出现过于密集的问题,这与图4中的实际效果是一致的。在图5(c)、图5(d)、图5(g)、图5(h)中,也即点云二,靠近水平刻度0的几个频数分布有显著差异,体素网格方法得到的靠近水平0刻度的几个频数分布直方图较高,而新方法对应的那几个频数直方图则非常低,这表明体素网格方法得到的采样点有相当一部分靠得非常近,而新方法则没有出现这个问题,这与图4中的实际效果也是一致的。

图5 频数分布图Fig.5 Frequency Distribution
根据计算得到的降采样后的点云中各个点到其最近点的距离,接着计算出这些距离的平均值和标准差,并找出这些距离中的最小值、最大值,这些数值,如表5所示。从表5可知,对点云一,体素网格和新方法得到的降采样后的点云的距离平均值和标准差都非常接近,这说明两种方法得到的点云总体没有明显差异;对点云二,距离平均值则有显著差异,新方法得到的点云的距离平均值明显大于对应的体素网格法,而新方法的距离标准差皆小于对应的体素网格法,这说明新方法得到的点云在原始点云中的分布更均匀。

表5 体素网格法和新方法得到的点云中各个点之间的最近距离,长度单位mmTab.5 Nearest Distances Between Downsampling Points Obtained by the Voxel Grid and Proposed Methods,Length Unit in mm
从上面的实验数据和分析可见,当点云轴向包围盒在x,y,z轴方向的最长边与最短边的比值较小,比如点云一最长边与最短边比值为2.4,体素网格法和新方法降采样的效果差别较小;当点云轴向包围盒在x,y,z轴方向的最长边与最短边的比值较大,比如点云二最长边与最短边比值为5.6,体素网格法和新方法降采样的效果差别非常明显,此时新方法优于体素网格法。
将表4中的体素总数和计算时间数据分别绘制出来,如图3所示。从图3明显可见,降采样的计算时间折线走势与体素总数曲线走势一致,可见降采样的计算时间与体素总数大致成线性关系,也即体素越多,降采样所需要的计算时间也越长。从图3我们还可看到,对同一个点云,当降采样后的点数相当时,新方法得到体素数量通常比体素网格法要少,因而新方法通常比体素网格法的计算速度更快。

4 结论
当点云轴向包围盒在x,y,z轴三个方向的边长相差非常悬殊的时候,传统的体素网格降采样方法就存在着采样点分布不均匀的问题。这是因为传统的体素网格法不考虑轴向包围盒的边长差异,直接将点云的轴向包围盒沿各个坐标轴方向皆分成n等份,最终导致包围盒最短边所在方向的采样点分布比最长边所在方向的采样点分布要密集得多,也即采样点在空间分布不均匀。针对这一问题,提出了一种新的体素网格降采样方法。该方法首先对点云建立轴向包围盒,然后以某一个等分距离对包围盒沿x,y,z轴三个方向的边进行等分,使得每一个体素近似为一个正方体,然后计算每一个体素内所有点的重心,并将其作为该体素的采样值。从实验结果可见,当降采样后的点数大致相同时,若点云包围盒在x,y,z轴三个方向的边长相差不大,新方法和传统体素网格法获取的点云分布均匀程度相当,但若点云包围盒在x,y,z轴三个方向的边长相差非常悬殊,新方法比传统体素网格法获取的点云分布更均匀。而且,新方法的计算效率高于传统的体素网格法。

