圆柱齿轮自由曲面铣削下的齿形误差研究

陈丹萍，廖宇兰，周 汉，苏 明

（1.海南科技职业大学机电工程学院，海南海口 571126；2.海南大学机电工程学院，海南海口 570228）

1 引言

自由曲面铣削是一种新型的柔性齿轮加工技术，可用于外齿轮的加工，尤其适用于具有复杂几何形状的新型齿轮。近年来，齿轮的自由曲面铣削已显示出其巨大的潜在优势，并越来越具有工业应用价值［1］。

虽然工业上通用多轴加工中心可以实现齿轮的自由曲面铣削，传统的自由曲面理论和方法［2−4］可以被认为是齿轮制造的基础。国内外研究学者在齿轮铣削误差方面开展了大量研究，文献［5］针对锥齿轮的几何误差控制，从影响加工误差的因素方面建立了数学模型，研究了加工误差的影响规律。文献［6］在传统单齿轮加工工艺基础上，研究了齿槽加工顺序与铣削均匀度的影响关系，在此基础上优化了数控加工程序。文献［7］针对人字形齿轮的铣削加工精度和效率方面，基于残差控制法建立了刀具路径的数学模型，通过实验验证了立铣刀加工模型的有效性。文献［8］在数控铣床上研究了一种新型凸凹齿轮的加工时间，结果表明随着模数的增加、齿数和铣削角度的增加，加工次数增加。文献［9］提出了一种精确五轴侧铣螺旋锥齿轮或准双曲面齿轮的数控编程创新方法。其他比较典型的铣削误差研究如文献［10−13］所述。

上述研究为铣削技术的研究提供了重要参考加载，这里通过对圆柱齿轮表面几何特征与铣刀的运动关系进行建模，研究了自由曲面铣削加工圆柱齿轮的齿形误差，分析铣刀类型、铣刀进给策略、齿轮基本参数等加工参数对齿形误差的影响。最后在标准立铣床的通用多轴加工中心上进行了实验验证。

2 齿轮自由铣削的几何分析

2.1 自由曲面铣削齿轮的数学模型

自由曲面铣削齿轮加工结合了专用齿轮机床传统制造方法和通用机床的集成数控加工方法。齿面由铣刀的扫掠运动产生，立铣刀铣削圆柱斜齿轮自由曲面的示意图，如图1所示。笛卡尔坐标系Sm（Om−xmymzm），Og（Og−xgygzg）以及St（Ot−xtytzt）分别建立在机床、工件和铣刀上，铣刀参数a和e表示铣刀在xm轴方向和ym轴方向的位置。在齿轮的自由铣削中，工件和铣刀绕各自轴旋转，铣刀沿着zt轴从齿轮宽度的上部向底部进给，此时工件围绕zg轴旋转φ角度。随后铣刀沿xm轴进给一定量，然后铣刀沿着zt轴从齿轮宽度的底部向上部进给，与此同时，工件围绕zg轴旋转−φ角度，整个齿侧以及所有齿面均采用这种方式加工。

图1 立铣刀铣削圆柱斜齿轮自由曲面的示意图Fig.1 Schematic Diagram of Milling Free−Form Surface of Cylindrical Helical Gear with end Mill

对于普通渐开线螺旋面［14］，如果齿面参数为（u，θ），则在铣削点的齿侧位置向量和法向量可表示为：

式中：rb—基圆半径；

σ0—基圆上的半角齿厚；

p—斜齿轮的螺旋参数。

通用立铣刀示意简图，如图2所示。Ot为铣刀位置点，P为铣刀表面上的铣削点，H、L为铣削点的坐标参数，αt和ψ分别表示铣削刃的倾斜角和铣刀绕xt轴的旋转角。

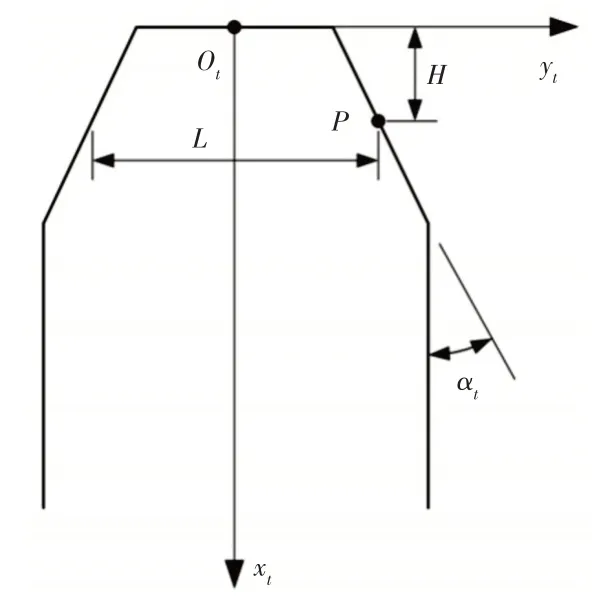
图2 通用立铣刀的参数定义Fig.2 Parameter Definition of Universal end Mill

因此，立铣刀在铣削点处的位置向量和法向量可以表示为：

式中：αt—铣削刃的斜角；ψ—铣刀绕xt轴的旋转角度。

通过坐标变换，工件坐标系Sg到加工坐标系统Sm的传递矩阵可以表示为：

式中：Mmg—Sg到Sm的传递矩阵

φ—旋转角度；p—斜齿轮的螺旋参数。

同样，从铣刀坐标系St到加工坐标系Sm的传递矩阵可以表示为：

式中：Mmt—St到Sm的传递矩阵—铣刀参数，用来描述xm轴方向和ym轴方向的铣刀位置点。

为使工件矢量与铣刀矢量相匹配，可以根据式（3）、式（4），通过改变齿形生成参数u，得到齿形上任意一点的旋转角度φ以及铣刀设置参数（a，e），从而可以推导出齿形上任意一点的铣刀位置点。

2.2 考虑残余误差的铣刀路径的计算

在齿轮自由成形铣削过程中，在满足齿形精度的基础上，计算铣刀轨迹以逼近理论齿面，而不是计算齿面上的所有刀位点。以普通立铣刀自由铣削直齿轮为例，考虑残余误差在内的铣刀路径计算，如图3所示。点A是与齿廓相切的第一个铣刀位置点，点B是与齿廓相切的相邻铣刀位置点，点C是这两条切线AC和BC的交点，点D是图面中齿廓曲线的法线交点。对于直齿轮，线CD的长度表示渐开线齿廓平面内的残余误差Δt，对于斜齿轮，需要在与表面正交的方向上测量表面误差。

图3 立铣刀自由铣削直齿圆柱齿轮的残余误差Fig.3 Residual Error in Free Milling of Spur Gear with end Mil

假设坐标A（xA，yA）、B（xB，yB），C（xC，yC）、D（xD，yD），由于AC和BC两直线与齿廓相切，因此AC和BC的斜率kA和kB可以表示为：

对于渐开线齿轮横向齿廓，螺旋参数θ=0，因此式（1）中法向量ng（u，θ）表示为ng（u，0），将ng（u，0）代入式（5），则斜率为kA和kB可以表示为：

同时，点C是两条切线AC和BC的交点，C（xC，yC）表示为：

由式（1）可知，点A、点B、点D在渐开线齿廓上，渐开线角分别为uA，uB和uD。此外，由于直线CD垂直于点D处渐开线的切线，且点D处的斜率kD为tan（σ0+uD），可得式（8）的几何关系：

式中：Δt—齿形残差。将坐标A（xA，yA）、B（xB，yB），C（xC，yC）、D（xD，yD），斜率kA，kB和kD添加到式（8），则有：

通常给定起始铣刀定位点A和齿形精度要求，即uA和Δt已知。根据式（9），可以推导出齿廓上铣刀位置点的参数（uB，uD），然后根据已知的uB作为起始值，可以推导出铣刀位置点的其他参数（uB1，uD1），同样可以获得铣刀位置点的所有参数（uBi，uDi）。立铣刀自由曲面铣削直齿轮，通过数值分析模拟了采用立铣刀的渐开线轮廓上的铣刀路径，如图4所示。

图4 立铣刀自由曲面铣削直齿轮Fig.4 End Mill Free−Form Surface Milling Spur Gear

3 齿形误差分析

本节将讨论自由铣削齿轮的过程中，铣刀类型、铣刀进给策略、齿轮基本参数等加工参数对齿形误差的影响。

3.1 关于齿形误差的铣刀类型

在自由铣削齿轮的过程中，不同类型的铣刀导致不同的加工效率和不同的齿面结构。与齿形误差相关的铣刀类型，立铣刀的侧边与齿面相切，而球头铣刀的顶部圆弧边与齿面相切，不同类型的铣刀会导致不同的加工时间，如图5所示。铣削道次与残余轮廓误差之间的关系，可以看出在本当前铣削参数条件下的残余轮廓误差范围Δt=（0.005~0.03）mm，如图6所示。

图5 铣刀的类型Fig.5 Types of Tool

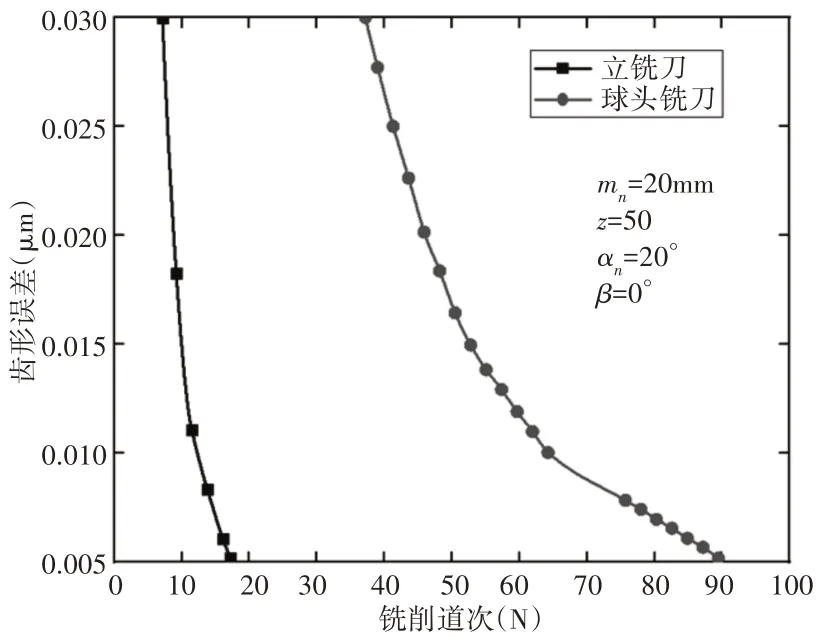
图6 铣削道数与残余轮廓误差的关系Fig.6 Relation Between Cutting Pass Number and Residual Profile Errors

对于立铣刀，铣削道次从17个减少到7个，对于球头铣刀，铣削道次从90个减少到37个。即当Δt=0.03mm时，立铣刀的铣削道次为7，球头铣刀的铣削道次为37，采用垂直铣削策略的球头铣刀，加工时间是采用切向铣削策略的球头铣刀的5.3倍。因此，与采用立铣刀制造齿轮相比，采用相同铣削道次的球头铣刀将产生更大的残余轮廓误差，且需要更多的加工时间。

3.2 齿形误差的铣刀进给策略研究

铣刀的进给策略也决定了齿形误差和加工时间。齿轮自由铣削加工过程中主要有三种进给策略：

（1）等渐开线角进给策略；

（2）等径进给策略；

（3）等残差轮廓误差进给策略。

立铣刀自由铣削齿轮的进给策略，如图7 所示。在图7（a）中，可以看出对于每条铣刀路径，铣刀进给是沿齿廓方向等距的，其渐开线角度Δui相等。根据渐开线齿形的特点，常数Δui表示从齿顶到齿根减小的齿形误差Δti，如图8所示。在图7（b）中，可以看出每个铣刀路径的铣刀进给都是等距的，沿轴向方向径向进给Δx。在图7（c）中，铣刀进给在每个铣刀路径上的距离相等，沿齿廓方向的残余误差Δt相同。也就是说，齿顶和齿根处的表面粗糙度相同，进给策略将直接影响齿形误差，下一节将讨论进给策略与齿形误差之间的关系。

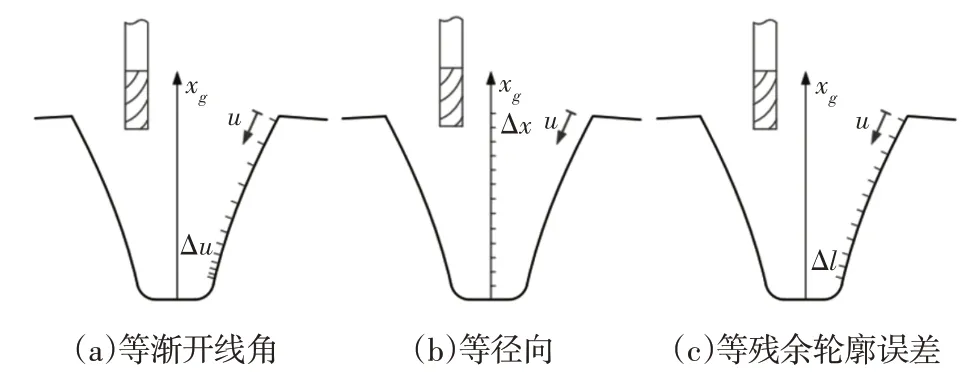
图7 立铣刀铣削齿轮进给策略Fig.7 Feed Strategy for Milling Gears with End Mills

图8 等渐开线角进给策略Fig.8 Feed Strategies of Equal Involute Angle Along Tooth Profile

为了分析进给策略对齿形误差的影响，在相同的铣削道次（N=14）下模拟了三种进给策略。等渐开线角的进给策略，如图9（a）所示。可以看出齿形的残余误差从齿顶到齿根呈减小趋势，齿形的最大误差为0.011mm，最小误差为0.0045mm，分别发生在齿顶和齿根上。从图9（b）中可以看出，采用上述等径向进给策略，齿形残余误差从齿根到齿顶呈现减少趋势，齿形的最大误差和最小误差分别为0.012mm 和0.007mm，分别出现在齿根和齿顶上。

图9 进给策略对齿形误差的影响Fig.9 Influence of Feed Strategy on Tooth Profile Error

由图9（c）可以看出，在等残齿形误差进给策略下，齿形残余误差基本一致，最大齿形误差为0.008mm。因此，从制造的角度来看，在给定最大齿形误差的情况下，铣削道次越少，效率越高，即等残余轮廓误差的进给策略是最优的，等径向进给策略是最差的。但在可能的情况下，可以考虑采用等径向进给策略和等渐开线角进给策略进行特殊轮廓的修形。

3.3 齿形参数对齿形误差的影响

从经济角度方面考虑铣刀路径的设计中，必须考虑工件参数，因为一旦确定了铣刀和所应用的铣削技术，齿形误差将由齿轮的齿形参数决定。本研究在相同的铣削道次（N=14）下，分析由于工件参数（如齿数z、齿模mn、压力角αn和螺旋角β）变化而导致的齿形误差，如图10所示。从图10（a）中可以看出，齿数的增加将导致两侧齿形误差的减小。在图10（b）中，可以看出当改变齿模时，齿模的增加将会导致两侧齿形误差的增加。在图10（c）中，可以看出压力角的增大将导致齿形误差减小。在图10（d）中，可以看出增大螺旋角将导致齿形误差减小。

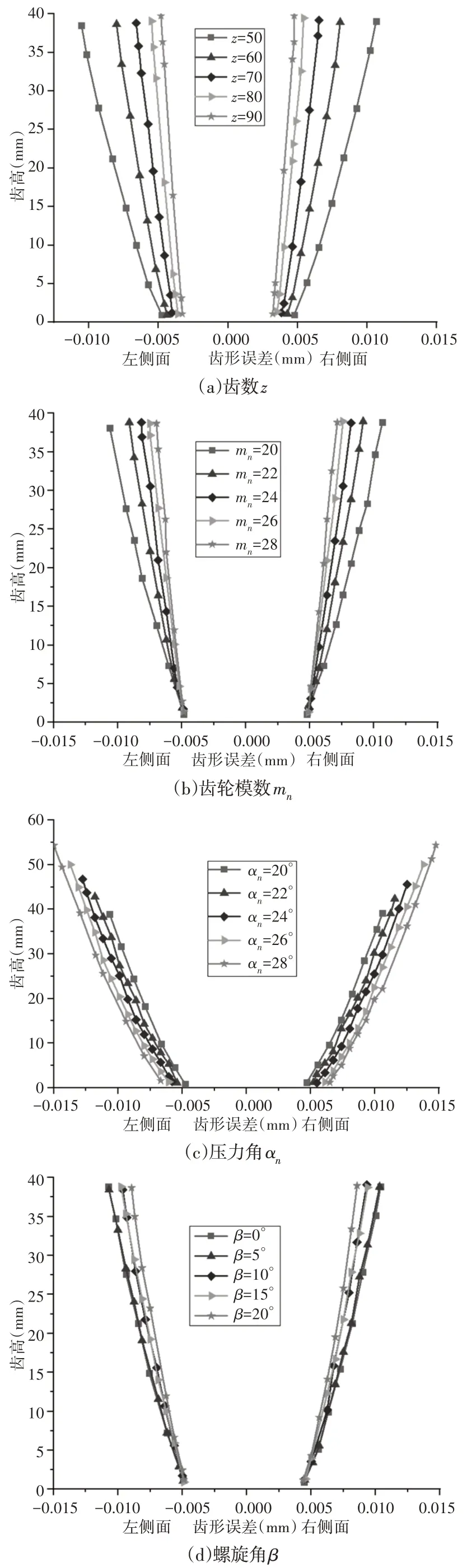
图10 齿形参数与齿形误差的影响关系Fig.10 Influence Relationship Between Tooth Profile Parameters and Tooth Profile Error

如前所述，齿形是由工件参数生成的，给定齿轮齿形误差后，铣削道次随着齿数的增加而减少，压力角和螺旋角也随之减少。但对于齿模越大的齿轮，铣削道次则越多。因此，在工件参数变化的情况下，应根据加工精度和效率的要求重新计算铣削道次。

4 实验研究

为了验证所提出数值分析模型的合理性，在大型多轴机床上对典型人字齿轮进行加工实验，如图11所示。机床有X轴、Y轴、Z轴和U轴四个直线轴，A轴和C轴两个旋转轴，可以采用通用铣刀加工各种类型和尺寸的齿轮。实验中铣齿的基本参数，如表1所示。

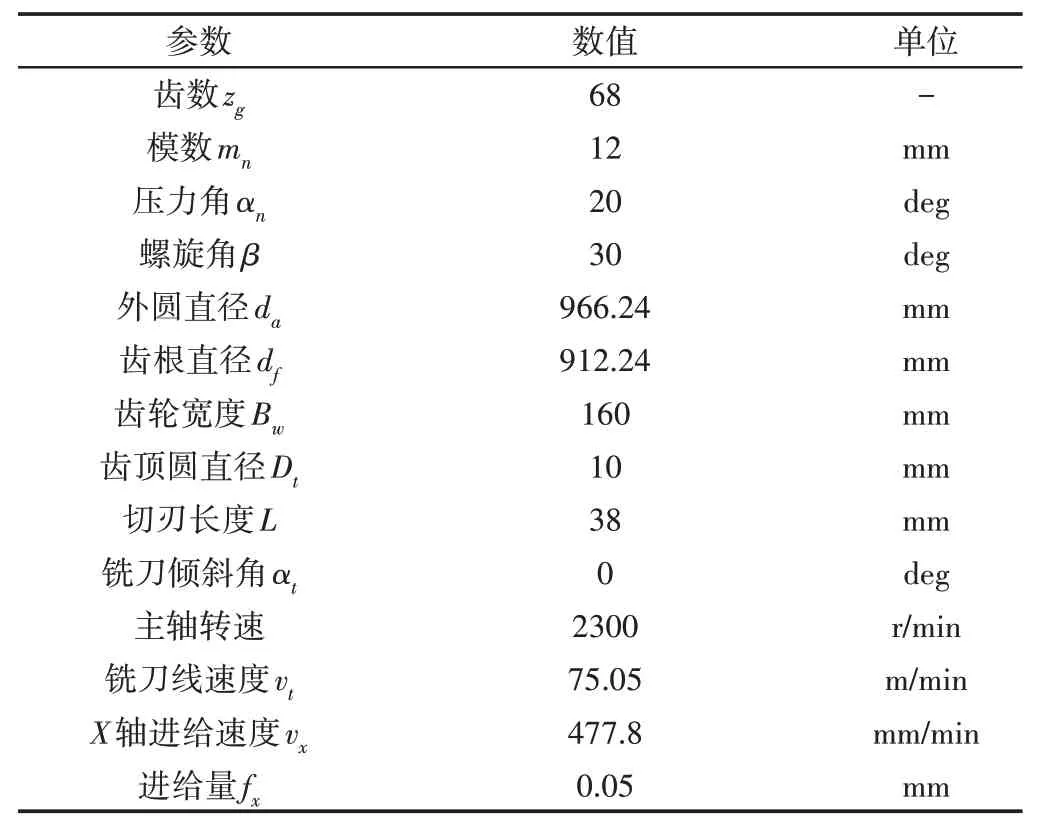
表1 实验的参数设置Tab.1 Parameter Settings of the Experiment

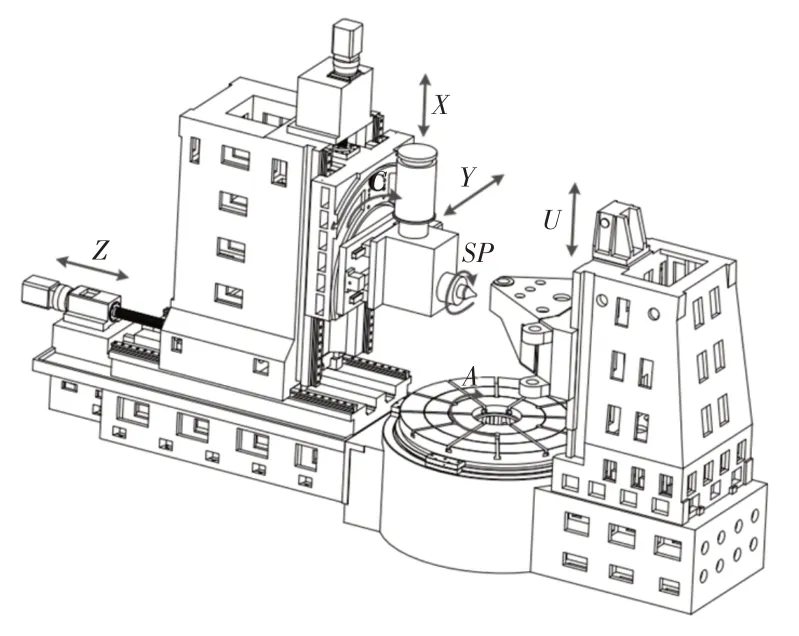
图11 自由曲面铣削齿轮的通用机床Fig.11 Universal Machine Tool for Milling Gear with Free−Form Surface

由于工件是一种特殊的人字齿轮，没有凹槽，通过传统生成方法或成型方法无法完成加工，而通过自由曲面铣削方法，可在通用机床上采用标准铣刀进行加工，立铣刀铣削齿轮自由曲面实验，如图12（a）所示。

图12 立铣刀铣削齿轮自由曲面实验Fig.12 Experiment on Milling Gear Free−Form Surface with End Milling Cutter

利用在机测量系统对齿轮齿形误差测量，从在机测量结果可以看出在自由曲面齿轮铣削中，齿形误差与工艺参数有直接关系。在相同的铣削道次（N=10）下，齿形残余误差在很大程度上依赖于所给定的进给铣刀路径。

对于等渐开线角度进给策略，通过在机测量系统测量得出图12（b）中的最大误差为0.007mm，该误差位于齿顶上。对于等径进给策略，通过在机测量系统测量得出的最大误差为0.006mm，该误差位于齿根上。对于等残差齿形误差进给策略，通过在机测量系统测量图12（c）的齿形误差最大为0.0045mm。此外，沿齿廓方向的误差大小基本相等，表明针对齿轮自由铣削过程中的不确定因素，实验结果与数值分析结果具有较好的吻合性。此外，采用不同铣刀类型的对比试验表明，如果两种铣削方法对残余齿形误差的要求相同时，则采用切向铣削方法的立铣刀比使用球头铣刀的铣削效率更高。

5 结论

研究了自由铣削圆柱齿轮的齿形误差，通过建立自由曲面铣削的数学模型，分析了铣刀类型、进给策略、齿轮基本参数等加工参数对齿形误差的影响。在铣刀类型的选择上，如果给定残余轮廓误差，采用顶刃与齿面相切的球头铣刀的加工时间大于侧刃与齿面相切的立铣刀。在进给策略方面，给定最大齿形误差时，等残余齿形误差的进给策略为最优，等径向进给策略为最差。在齿形参数的选择方面，可以通过增加齿数、压力角和螺旋角来减小齿形误差。研究结果可为自由曲面铣削加工参数的选择提供理论依据。