基于可制造性特征的制造资源建模

赵昌龙，杨俊宝，李明，赵钦祥，马洪楠，贾晓宇

(长春大学机械与车辆工程学院，吉林长春 130022)

0 前言

随着工业发展步伐的加快，许多新的智能制造技术应运而生。如数字孪生技术，它是利用计算机程序实现虚拟与实际加工之间的交互，对实际过程进行虚拟控制，从而降低成本、提高生产效率[1-2]。然而，数字孪生技术在实际生产过程中需要选择设备能加工的特征。随着现代设备不断发展，一个设备可以实现多种加工工艺，不同设备之间的工艺差别变得越来越模糊。因此，为提高实际生产效率，本文作者提出一种混合算法，将遗传算法(GA)和模糊C均值聚类(FCM)算法相结合，根据制造资源的可加工特征对制造资源进行分组。该混合算法既具有GA的全局搜索能力，又具有FCM的局部搜索能力，可以同时获得最佳聚类数量和最佳分组，从而减少设备的搜索时间和搜索空间。

1 基于Object-Oriented方法的制造资源信息建模

1.1 制造资源模型需求与结构

利用Object-Oriented方法的封装和派生等优势，构建Object-Oriented类分层结构模型。类是Object-Oriented方法中的主体，描述了一组对象公有的属性和服务，类可以进一步派生为子类，子类在主体的基础上，再添加自己特有的属性和服务。

根据可制造性评价内容，制造资源模型包括制造设备类、技术设备类和特征类信息模型。制造设备类信息模型主要为加工设备，包括铣床、磨床、车床等设备。磨床包括外圆磨床、内圆磨床和平面磨床，外圆磨床包括数控外圆磨床和万能外圆磨床等设备。技术装备类信息模型包括刀具、夹具、量具等。特征类信息模型包括制造资源模型中设备可以加工的特征，如平面、孔、凹槽等，如图1所示。

图1 制造资源模型

加工设备的Object-Oriented信息模型包含加工设备的基本信息和加工能力信息两部分。机床的基本信息模型如图2(a)所示，设备特征加工能力模型如图2(b)所示，刀具和特征基本信息模型分别如图2(c)和图2(d)所示。

图2 Object-oriented信息模型

部分程序如下所示：

机床基本信息定义：

class MachinetoolInformation//机床基本信息类

{

int GroupID；//机床的加工设备分组编号

int MachineID；//机床编号

stringMachinename；//机床名称

stringMachinetype；//机床型号

stringMachineowner；//机床所属单位

stringProcessfeature；//机床所能加工的特征

int MatchingfixtureID；//可匹配夹具编号

......

public：

void add()；//添加函数

void delete()；//删除函数

void alert()；//修改属性函数

......

}

车床基本信息类定义：

class LathInformation：publicMachinetoolInformation

{

double Maximumstroke；//顶尖套最大行程

double Taperangle；//顶尖套锥度

......

}

机床的特征加工能力信息类定义：

class ProcessCapability

{

int FeatureID；//特征编号

string Featurename；//特征名称

int FeatureownerID；//特征所属设备编号

double Maxlength；//机床能加工的最大长度

double MaxRa；//能达到的最高表面粗糙度

......

public：

void add()；//添加函数

void delete()；//删除函数

void alert()；//修改属性函数

......

1.2 基于制造资源约束的可制造性评价

零件可制造性是指零件可以适应现有制造资源的程度，包含加工成本、加工时间、加工技术和装配过程等因素[3]，并在此基础上，建立制造资源模型。基于制造资源约束的可制造性评价过程如图3所示。

图3 基于制造资源约束的可制造性评价

步骤1，输入制造特征。在数据库中搜索特征信息，如果发现特征，则可以加工零件；否则，零件无法加工。

步骤2，根据零件设计要求，搜索特征对应的制造设备组。如果找到可以加工该特征的设备，就可以加工该零件；否则，有限的制造资源无法加工该零件。

步骤3，在数据库中搜索技术设备信息。如果根据设计要求找到合适的刀具和夹具，零件就可以在现有的制造环境中进行加工；否则，零件无法加工。

可制造性评价的两个方面：(1)测试零件是否可以被现有制造资源加工；(2)决定零件如何低成本、有效地加工。第一步只关注制造资源，第二步根据不同客户的要求找到处理零件的最佳方法。制造资源建模的总体流程如图4所示。

图4 制造资源建模总体流程

2 基于特征的加工设备分组

制造过程包含许多特征，如平面、孔、盲孔、阶梯、凹槽和曲面等，加工设备根据设备可加工的特征进行分组。然而，由于零件尺寸、公差要求和其他重要的制造标准不同，相同的特征不能总是由相同的设备加工。本文作者除了考虑制造特征外，将设备加工能力(包括设备加工零件的尺寸及加工精度)也添加到制造资源模型中。在基于特征的制造资源划分中，共有N个加工设备和s个特征，加工设备向量可以通过公式(1)和(2)定义。

xi=(xi1,xi2,…,xis,pi,ai)i=1,2,…,N

(1)

k=1,2,…,s

(2)

3 FCM和GA混合算法

3.1 FCM算法

FCM算法是一种无监督的非参数化方法，通过聚类来分析数据。该技术于1973年首次提出，由于它具有良好的稳定性、分区质量及收敛性，一直被广泛应用。FCM算法收敛性证明如下：

由此看来，技艺只是手段而非本体，与物性展开对话，会使艺术家摆脱因自以为是的独门绝技去以偏概全、一意孤行。我们说艺术是自由的，每个人都能在这片天地里寻找自己、获得自己，但过度强调技艺的作用，往往会增加物我之间、观念与材料之间的更多隔阂。只有尊重对象的存在，通过对话才能激活物性的魅力。这正是海德格尔所赞美的“凝固着人的经历”的物性，不是自我表现，而是人性与物性、技艺与现实的唯一“存在”，不可分离。

给定一组对象X=(x1，x2，…，xN)，xi∈RS，其中N是对象的数量，S是模式向量的维数。用FCM划分区域，使目标函数最小化，如公式(3)所示：

(3)

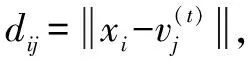
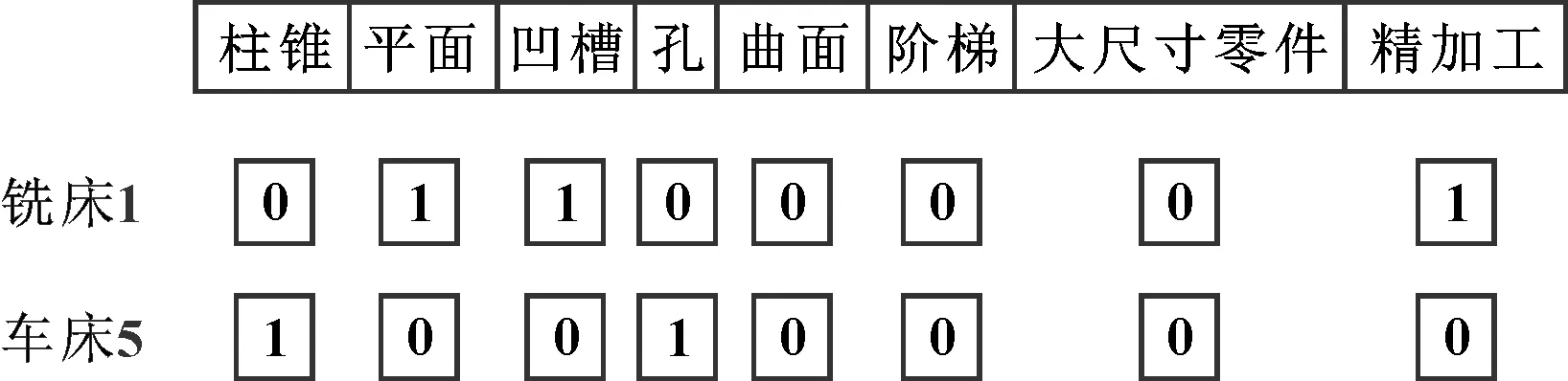
标准的拉格朗日乘数最小化方法可以在公式(3)中调用，以获得更新后的聚类中心点向量和隶属函数矩阵。给定一个固定数C(2≤C

(4)

(5)

3.2 遗传算法(GA)

1975年，J HOLLAND教授受进化论的启发，提出了遗传算法(GA)。物竞天择、适者生存是自然界的生存规律，在一个物种缓慢进化的过程中，基因随时可能发生变化。如果这些变化对自然选择有帮助，则会形成一个新物种；相反，则会导致种群灭绝。GA的出现取代了许多计算成本高的确定性优化方法，在工程领域越来越受欢迎[4-5]。

3.3 混合算法

FCM算法是一种局部搜索算法，它对初始化敏感，在计算过程成中容易进入局部最优状态，并没有达到人们的期望[6]。GA是一种在实践中广泛使用的全局优化算法，它不但具有普遍性和简单性等优点，还具有良好的鲁棒性和并发处理能力[7]。基于两种算法各自的优势，混合算法不仅具有GA的全局搜索能力，还具有FCM算法的局部搜索能力，解决了FCM算法对初始化敏感的问题，并提高收敛速度，可以更有效地完成聚类工作。

混合算法包括外层迭代和内层迭代。外层迭代利用GA获得最优聚类数，内层迭代利用基于GA的FCM算法确定最优聚类数所对应的最优分区。

3.3.1 内层迭代

由于在内层迭代中引入了GA和FCM的混合算法，根据最大隶属度原则，可以得到与聚类数量对应的最优分类矩阵。混合算法的主要功能包括编码、构建适应度函数、选择遗传算子和确定参数等[8]。

(1)编码。浮点数编码方法具有精度高、收敛速度快、便于大空间搜索等优点。聚类的目的是获得数据集的模糊划分矩阵U和聚类中心V，而U与V是相关的，所以文中通过浮点数编码方法对聚类中心V进行实际编码，从而减少算法的运算量并提高算法的搜索效率[9]。一个染色体表示为fchr=v1v2…vC，其中C是聚类数量，每个聚类中心V有S个字符，染色体长度为C×S，表示为{v11,v22,…,v1S,v21,v22,v2S,…,vC1,vC2,…,vCS}。

(2)适应度函数。模糊聚类问题实际上是优化问题，目的是为了获得最小的目标函数(损失函数)[10]。在优化过程中确定下一代个体生存概率的染色体适应度值是一个重要问题，模糊聚类的目标函数Jm越小，分区越合理，GA的适应度函数越大。目标函数Jm的适应度函数如下：

(6)

(3)交叉和变异算子。GA中最重要的算子是交叉算子，在交叉过程父母的两个染色体结合形成一个新染色体。交叉算子在遗传过程中，良好的染色体基因在群体中频繁出现，使整体收敛[11-12]。两个个体fchr1和fchr2交叉运算后产生两个新个体分别为

f′chr1=αfchr1+(1-α)fchr2

f′chr2=αfchr2+(1-α)fchr1

(7)

式中：α为个小于1的常数。

变异算子在GA中起着关键作用，能够在染色体进化过程中引入随机变化。交叉算子使种群中的染色体相似，进而种群收敛，而变异算子将随机变化引入种群，避免局部最优。对个体进行变异操作后得到变异后的个体为f′chr：

f′chr=x1x2…x′i…xn

x′i=Umin+γ(Umax-Umin)

(8)

式中：[Umin，Umax]为基因取值范围。

(4)选择算子。典型的GA不能保证结果收敛到全局最优解，当GA与最优个体保存策略一起应用时，可以产生全局最优解[13-15]。混合算法中的选择算子是通过将剩余随机抽样与替换和最优个体保存策略相结合来进行的。带有替换的剩余随机抽样优点是子代中具有高适配度的个体能以最小的选择误差被保留下来，具有最大适应度函数值的个体被保留在后代中。

(5)个体的FCM优化。使用FCM优化方法，可以提高收敛速度，增强局部搜索能力[16]。FCM优化步骤如下：①通过公式(5)计算染色体代码，得出相应的模糊矩阵U。②通过公式(4)计算出新的聚类矩阵U，得出新的聚类中心，并对其进行编码，生成新的染色体。③通过重新计算目标函数值，发现种群中最差的个体，并用在选择过程中始终保持最优的个体来代替。

基于GA的模糊聚类算法内层迭代步骤如图5所示。

图5 混合算法流程

3.3.2 外层迭代

一个好的聚类算法既要考虑不同分区之间的离散程度，也要考虑一个分区的压缩程度。不同分区之间的离散程度可以表示为聚类中心之间的平均距离。聚类中心之间的平均距离值越大，不同分区的偏差程度越大。聚类中心之间的距离用D表示，计算公式如下：

(9)

聚类的主要目的是对数据集进行分区，使不同分区之间的距离最大化，聚类中每个对象之间的距离最小化。随着聚类数量C的增加，Jm值减小，D值增加，外层迭代的目标函数如下：

f=Jm(U,V)+D

(10)

外层迭代的适应度函数为

(11)

典型的GA中编码方法是对聚类数量进行二进制编码。选择算子采用剩余随机抽样与替换和最优个体保存策略相结合的方法。交叉和变异算子分别是单点交叉和基本变异，计算每条染色体对应的聚类数量，并通过内层迭代得到最优分组。

混合算法的实现过程如图5所示。

4 算法的实现

为了测试混合算法的有效性，对设备可加工特征进行划分，得到如图6所示的制造资源集，其中特征包括柱锥、平面、凹槽、孔、曲面和阶梯。加工设备由模式向量表示，长度为8，前6位数字代表柱锥、平面、凹槽、孔、曲面和阶梯，最后2位数字表示能否加工大尺寸零件，以及能否用于精加工。模式向量由0和1组成，如果设备可以加工该特征，则对应数值1，否则对应数值0。例如，铣床1可以加工平面、凹槽，但不能加工大尺寸零件，可用于精加工，即铣床1的模式向量为01100001。车床5也如此，如图7所示。使用文中提出的混合算法对设备进行分组，得到32台加工设备的模式向量如图6所示。

图6 加工设备及其属性

图7 加工设备向量

本文作者利用C++实现该混合算法，内层迭代和外层迭代的种群数量分别设置为40和20，进化代数设置为100，交叉率和变异率分别设置为0.8和0.1。

模糊聚类目标函数Jm和聚类中心之间的平均距离D随聚类数量的变化如图8所示。Jm随着聚类数量的增加而单调递减；D在(2，10)(11，12)范围内单调递增，在(10，11)范围内单调递减；当聚类数量为6时，Jm和D之和最小。外层迭代适应度函数随聚类数量的变化如图9所示：当聚类数量为6时，得到适应度最大值。根据混合算法得到的最优数量6，按照最大隶属度原则获得最优分类，分类结果如表1所示。

表1 制造资源的分类结果

图8 模糊聚类的目标函数值

图9 外部适应度与聚类数量关系

每个制造资源只属于一个类别，但每个特征可以属于多个类别。第2组和第5组可以加工中小型零件的柱锥和孔特征，同时第5组设备可用于精加工，这些设备可以处理相同的特征，但位于不同的分区组中。可制造性评价的主要内容是评价零件每个特征是否具有相应的加工设备，文中利用混合算法对加工设备进行划分，只需搜索具有评价特征的分组，搜索时间和空间就会减少，从而使可制造性评价效率提高。

5 结论

设计一种由GA和FCM组成的混合算法，根据设备可以加工的制造特征对加工设备进行分组，利用基于制造资源约束的Object-Oriented方法建立制造资源信息模型，设计可制造性评价框架，使用模糊规则来处理现代加工设备之间加工能力差异问题；构建混合算法的数学模型，利用GA的全局寻优能力，采用GA和FCM的混合算法动态确定最优分组数目和该数目下的最优分组，并在32台加工设备上对混合算法进行测试。结果表明：混合算法对初始值不敏感，成功减少了加工设备的搜索空间和搜索时间，验证了该算法的有效性。制造资源模型可以为计算机辅助工艺规划提供信息，更好地管理人工制造资源，有利于提高企业的整体业绩，使管理层的决策更加完善可行。文中提出的模型可以在未来进一步完善，引入更多制造特征，使信息更加精简、可制造性评价和决策更加有效。