基于灰色预测模型的水煤浆输送管道冲蚀磨损寿命预测

王硕，张亚新，朱博韬

（1 新疆大学化工学院，新疆 乌鲁木齐 830000；2 新疆大学煤炭清洁转化与化工过程自治区重点实验室，新疆 乌鲁木齐 830000；3 新疆大学省部共建碳基能源资源化学与利用国家重点实验室，新疆 乌鲁木齐 830000）

随着我国的工业化进程的推进，市场对石油与天然气产品需求量激增，石油与天然气相关产品的供求矛盾加剧，高度依赖进口填补空缺，已成为制约我国工业更高质量发展的瓶颈[1]。针对我国“煤多油少”的能源结构现状，我国自“十五”计划至今连续4个五年计划都对调整能源结构、发展煤化工产业做出长期规划，发展煤化工成为保障我国能源安全、减少能源对外依赖程度的主要途径[2]。

固液两相流广泛出现在煤化工管道系统中，因多相流冲蚀磨损产生的失效、非计划停工事故频发，成为制约煤化工装置安全运行的重大隐患[3-4]。一直以来，应对固-液两相流冲蚀磨损失效问题，主要采取更换更高级材料的管道或增加管道壁厚的方法来保证管道的安全运行，但此类被动方法不能有效减少管道突发性失效事故发生概率，而且大大增加了生产成本。据能源行业统计研究表明，使用此类方法后突发性的管道失效事故仍然有30%～50%来源于摩擦与磨损[5-7]，其中主要失效穿孔位置集中到了弯管部位，弯管部位冲蚀速率是直管部位的50倍以上[8]。因此，针对冲蚀磨损现象开展管道寿命预测成为保障煤化工生产设备稳定运行、预防突发穿孔事故、实现事前预控的重要手段。

近年来，针对设备所出现的冲蚀磨损现象，国内外学者使用实验与数值模拟方式展开了相关研究，叶福相等[9]应用喷嘴冲蚀实验方式分析了冲蚀磨损与化学腐蚀的协同作用，研究发现颗粒浓度是冲蚀磨损导致金属材料减薄的主要影响因素。Cao等[10]采用管流式冲蚀装置研究发现冲蚀位置主要集中在弯管出口方向上，而且以切削痕迹为主，冲蚀痕迹主要集中在外侧轴向60°～90°之间。数值模拟研究方面，Peng 等[11]采用CFD 与DPM 模型双向耦合方式探究了两相流条件下弯管中的冲蚀磨损规律，离散相颗粒因惯性力产生的二次流对管壁的刮擦现象，加剧了管壁的冲蚀磨损。

在管道寿命预测研究方面，国外学者Teixeira等[12]和Caleyo 等[13]应用Monte Carlo 模拟方式对承受内压的海底管道进行了一阶可靠性评估，分析了内压波动对管道可靠性的影响，并对管道进行剩余寿命预测。Singh 等[14]使用模糊数学理论叠加Monte Carlo 混合模型计算出含内缺陷管道的可靠性数学模型。国内学者胡群芳等[15]针对燃气管道内缺陷导致泄漏风险问题，使用贝叶斯理论模型非线性拟合出最大缺陷深度公式与预测结果的置信区间，极大便利了燃气管道风险评价工作。高旭东等[16]使用数值模拟与PARIS经验公式结合方式，模拟了管道缺陷裂纹扩展过程并通过数学模型预测其剩余寿命。骆正山等[17]使用粒子群优化法对灰色马尔科夫链模型进行二次光顺处理，所建立的修正模型精度比传统灰色预测模型高40%，实现了预测值与实际值的高度吻合。陈翀等[18]使用基于自适应遗传算法模型的机器学习方法，通过大量数据对模型的训练，对多因素影响下的埋地管道剩余寿命与更换周期做出评估。张进春等[4]基于数值模拟结果，使用“首次穿越模型”对煤气化输送管道进行可靠性分析，发现大管径管道在固液两相流环境中抗冲击性能更好，并对该管道的服役寿命与预防性检修周期给出建议。

国内外学者通过大量的冲蚀磨损实验与数值模拟研究，证实了冲蚀磨损是一种由固体粒子撞击切削所产生的局部金属减薄现象，且冲蚀导致的局部减薄速率要远高于腐蚀所造成的均匀减薄速率，但是单纯的影响因素与冲蚀磨损规律研究，对管道冲蚀失效的预防与事前控制工作指导意义有限。同时在管道寿命预测研究方面，大多数研究所应用的数理统计或机器学习等方法，都要基于大量的数据分析且要求数据符合一定的概率分布形式才能达到良好的预测效果，但冲蚀磨损减薄速度快，冲蚀失效突发性高以及测量投入成本高等特点导致难以积累大量实际检测数据，因此冲蚀磨损不适宜采用数理统计或机器学习的方式来进行预测[19-21]。

针对以上研究中出现的问题，本研究以新疆某煤化工企业水煤浆汽化炉进料弯管为研究对象，该管道在使用期间冲蚀减薄速度极快，企业凭借经验在极短周期内采取频繁更换和补焊的手段来防止突发性泄漏事故发生，导致生产效率不高。在弯管此类大曲率面上进行常规的壁厚在线检测工作难以取得准确结果，同时高温高压临氢环境下开展人工测量的成本投入与危险性极高，因此鲜有管道减薄数据的积累，成为该系统寿命预测面临一项难题，为此本研究使用ANSYS 2021R1对进料弯管的冲蚀磨损减薄量及冲蚀磨损位置进行研究，通过数值模拟收集初始数据后，使用基于小数据量建模的灰色预测理论进行数学建模，并对预测模型进行优化。根据国家相关标准，对煤化工煤浆输送管道做出寿命评估，对该设备的在役管道使用寿命与检修周期给出合理化建议。本研究为该装置的水煤浆输送管道冲蚀磨损减薄规律与寿命评估提供一种解决方案，对煤化工管道冲蚀磨损的预防与管道系统完整性研究提供一种研究方式。

1 冲蚀磨损速率数值模拟

1.1 几何模型建立与网格划分

以新疆某煤化工企业中水煤浆汽化炉进料管弯管部分为建模依据，该弯管的公称直径为DN100mm，弯径比1.5，弯管角度90°，在弯头进出口处添加了长度为5 倍管径的直管段。使用ANSYS SpaceClaim 2021R1 软件生成如图1 所示的几何模型。网格由ANSYS Meshing 2021R1 软件生成，采用Sweep方式以入口面为源面向后扫略生成六面体内嵌三棱柱型式的网格（图1），并在管壁内侧设有5层边界层，边界层生成增长率为1.2。

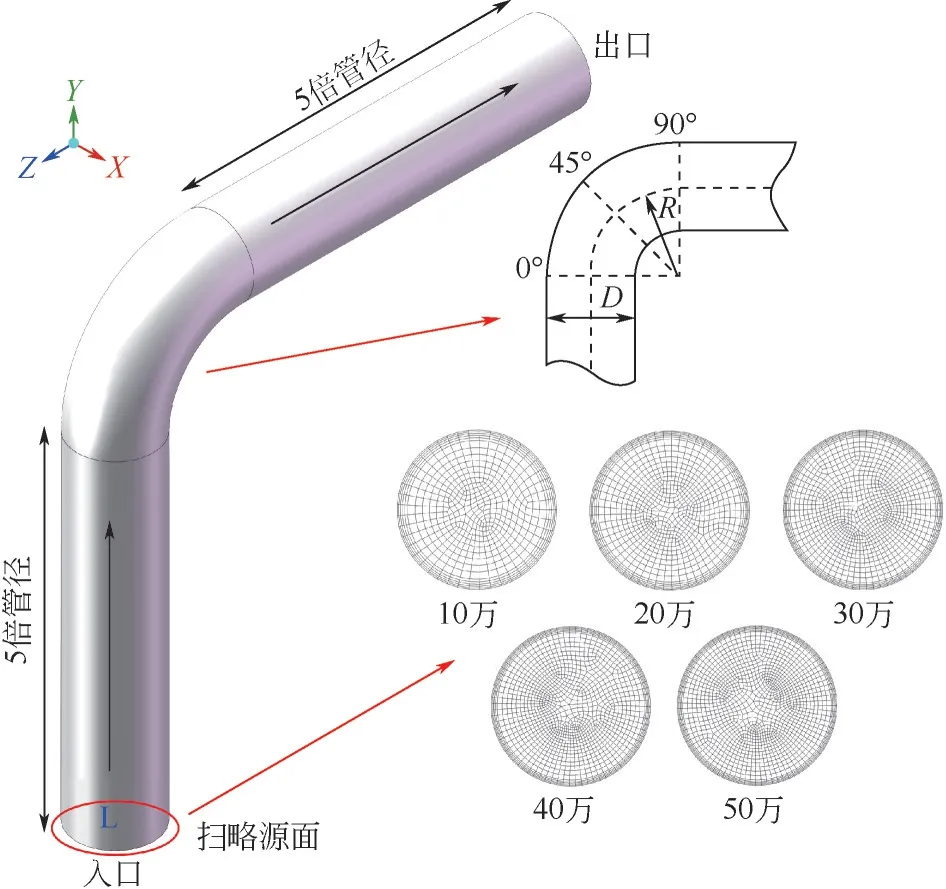
图1 几何模型与网格划分

1.2 数学模型

1.2.1 湍流模型方程

数值模拟研究中采用RNGk-ε湍流模型进行计算，该模型输运方程如式(1)、式(2)。

式中，Gk为平均速度梯度的湍流动能；Gb为浮力湍流动能；YM为可压缩流体湍流耗散；Sk、Sε为张量形式的源项；ε为湍流耗散率，W/m3；k为湍流动能，J。

1.2.2 DPM离散相受力方程[式(3)～式(6)]

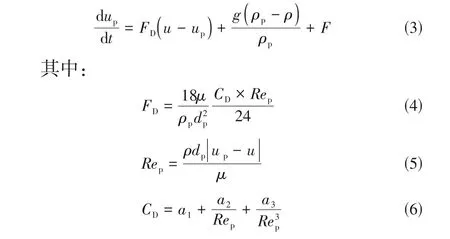
式中，u、up为连续相与分散相速度，m/s；ρp、ρ为连续相与分散相密度，kg/m3；F为附加质量力，N；FD(u-up)为单位颗粒质量所受阻力；dp为颗粒直径，m；μ为连续相黏度，Pa·s；a1、a2、a3为常数，根据雷诺数不同自行选取。

1.2.3 冲蚀磨损计算方程[式(7)]

式中，RE为冲蚀速率，kg/(m2·s)；mp为颗粒单位质量流率，kg/s；C(dp)为颗粒直径系数；f(α)为颗粒碰撞角函数；b(v)为相对速度；Aface为壁面单位表面积，m2。

1.3 无关性与模型准确性验证

1.3.1 网格无关性验证

几何模型采用上、下游直管段均为5倍管径的几何模型，由ANSYS Meshing 2021R1 生成以10 万网格数量为基础且逐级增加网格数量的5 套网格（图1），各套网格在各轴向角度上冲蚀速磨损量与网格数量关系如图2所示，网格数量到达30万的3套网格在各个轴向角度截面上的冲蚀磨损量已十分相近，最大冲蚀磨损量变化不超过3%。综合考虑计算效率与模拟准确性，采用数量为40 万的网格进行数值模拟计算。

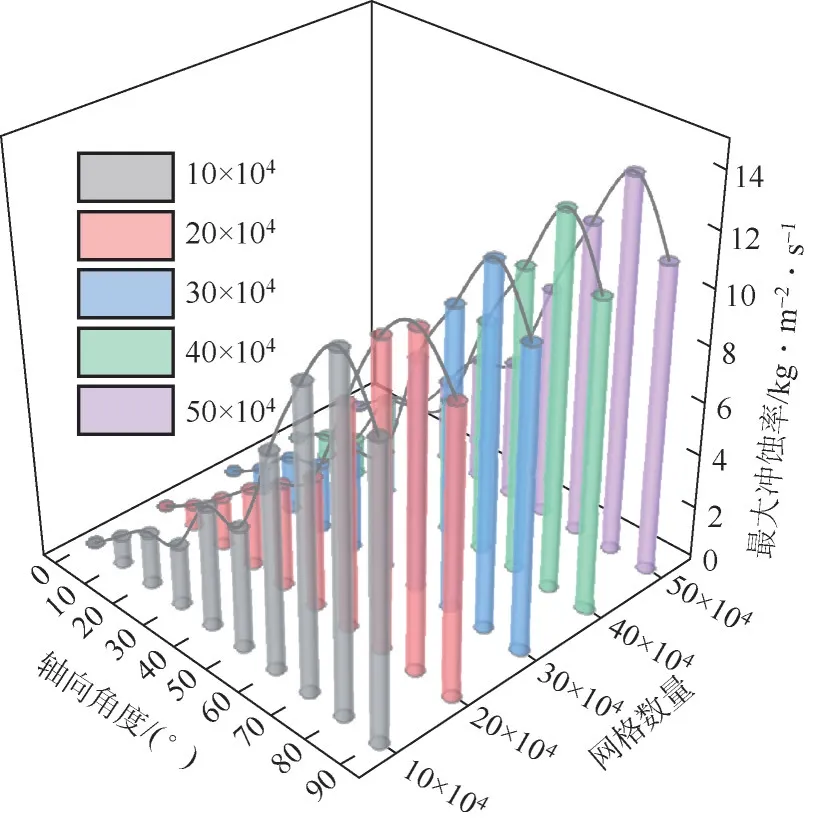
图2 不同网格轴向角度截面上冲蚀磨损率变化

1.3.2 模型准确性验证

彭文山[22]对固液两相流管道系统的冲蚀磨损现象进行了实验研究，管流式实验设备中介质流速为4.09m/s，离散相颗粒直径为0.3mm，颗粒质量流量为0.1027kg/s。在设置相同边界条件情况下，数值模拟结果与实验结果在冲蚀磨损位置以及冲蚀磨损速率上基本一致，由图3可以看出，本文数值模拟结果与文献实验结果误差小于5%。故鉴于模拟结果与文献实验结果的高度吻合，本文所建立的数学模型可以很好地描述管道内固液两相流的冲蚀磨损现象。

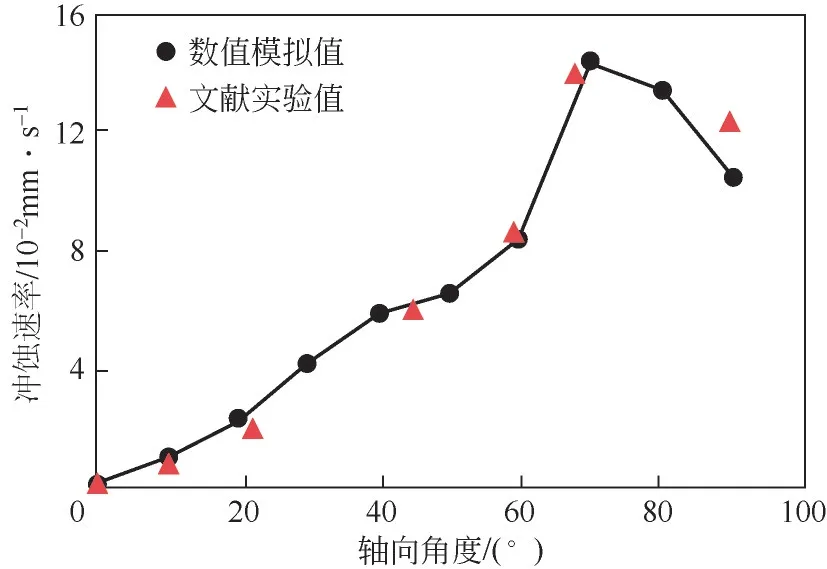
图3 轴向各角度冲蚀速率对比

1.4 边界条件

在ANSYS Fluent 求解器中采取欧拉-拉格朗日方式模拟固液两相流系统，其中连续相介质为水，密度为998kg/m3，沿入口法向速度为5m/s，离散相颗粒为煤粉颗粒，密度为1800kg/m3，速度与连续相介质保持一致，固体颗粒质量流量为0.5kg/s，颗粒相体积分数占比不足12%，故忽略颗粒与颗粒间相互碰撞，固体颗粒离散相与流体连续相间采用双相耦合方式，颗粒对壁面冲蚀磨损计算方式使用式(7)中的Generic 模型，颗粒与壁面间的反弹恢复模型使用Forder 模型[23]，压力与速度耦合方式采用SIMPLEC 算法，控制方程使用二阶迎风格式进行离散。

1.5 模拟结果分析

如图4所示在同样边界条件下，6组不同服役时间弯管的模拟结果表明冲蚀磨损主要集中在弯头区域内，直管段没有明显的冲蚀磨损现象。结合图中的流线，管内介质因为惯性作用直接冲击位置集中在弯曲部位，且均出现明显的速度损失现象，流线偏转与速度改变最为明显区域为中心截面轴向70°附近，从云图也可以看出该点处磨损减薄量最高，此位置即为该管道的最危险点。包括最危险点在内的冲蚀减薄量高的区域称为冲蚀磨损核心区，而其他受二次流等影响出现冲蚀磨损现象的区域称为冲蚀磨损影响区。随着服役时间的增长，冲蚀磨损核心区逐渐出现接近V形的磨痕[24]，冲蚀磨损核心区只出现略微的扩展且最危险点不随服役时间增长出现移动现象，而冲蚀磨损影响区域出现以冲蚀磨损核心区为中心向周围扩展的现象，且影响区扩展到一定程度后，范围不再发生扩展[图4(c)～(f)]。

图4 不同服役时间的冲蚀磨损减薄云图与流线图

6 组不同服役时间下的冲蚀减薄量如图5 所示均呈现轴向50°～80°冲蚀磨损率急剧高现象，磨损减薄量高于其他轴向角度至少20%以上。冲蚀磨损减薄量峰值在70°附近，最大磨损减薄量高于平均冲蚀磨损减薄量1个数量级。而当轴向角度大于70°后，冲蚀磨损减薄量出现明显下降趋势，结合图4 中流线可知，超过70°后两相流将不会出现与壁面的直接撞击切削，改为以二次流碰撞壁面为主的磨损形式，因此冲蚀磨损减量薄随之下降。

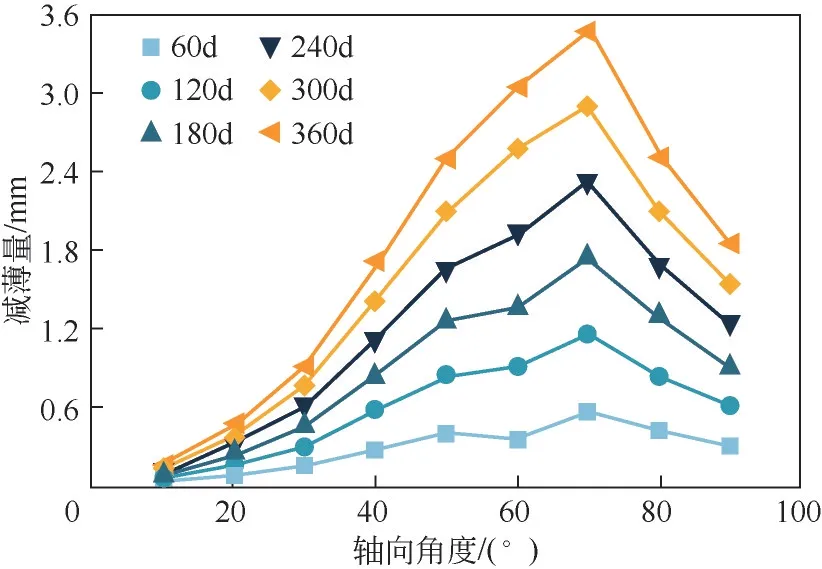
图5 不同服役时间减薄量

如图6所示不同服役时间的相同轴向角度下的减薄量增长率差值在-3.07%～4.05%之间，且差值变化无规律。同一服役时间内的各个轴向角度上的冲蚀磨损减薄量之间增长量同样呈现不规律变化，因此管道的冲蚀磨损减薄量变化是一个非线性的增长过程，且没有呈现出典型分布的特征，线性回归等统计学方法不适用于此类冲蚀磨损的预测，故具有小数据量建模、适用于不同数据类型等特点的灰色预测系统理论更适合对管道冲蚀磨损的预测。

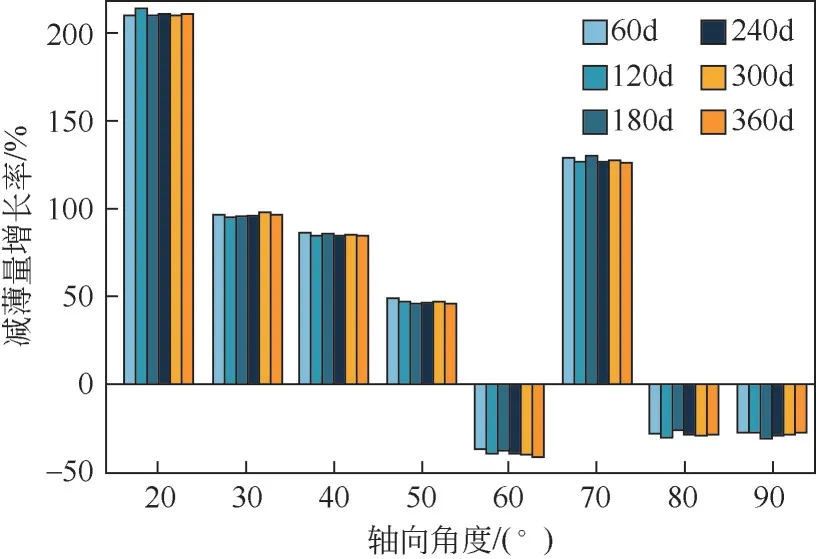
图6 减薄量增长率对比

2 预测模型建立

本研究使用灰色预测理论建立数学模型，该理论在1982 年由华中科技大学邓聚龙教授首次提出，是一门解决具有较高灰性或不确定性贫信息问题的横断科学，是一种研究小数据、贫信息不确定性系统的方法。该理论以“部分信息已知，部分信息未知”的“小数据”“贫信息”不确定性系统为研究对象，通过对“部分”已知信息的挖掘，提取有价值的信息，实现对系统运行行为、演化规律的正确描述与有效监控。现实工程实践过程中普遍存在的“小数据”“贫信息”不确定系统，为灰色系统理论提供了丰富的研究资源和广阔的发展空间，灰色预测理论在社会、经济、农业、工业、生态、生物等专业领域都有出色表现[25-29]。本研究中水煤浆输送管道的冲蚀磨损问题，因其在实际生产当中冲蚀磨损速率快、因成本与安全性考虑测厚数据积累少等问题成为“贫信息”系统，使用上一节中数值模拟得到的“小数据”对该水煤浆管道冲蚀磨损速率建立预测模型并做出一定的改进。

2.1 冲蚀磨损速率预测模型建立

2.1.1 GM(1,1)冲蚀磨损预测模型

将式(9)中微分方程根据最小二乘法估计原理建立如式(10)所示矩阵方程，通过式(11)中矩阵运算求解系统发展系数a与GM(1,1)模型的并净值b的最小二乘估计值。

确定a、b的估计值后一阶灰色预测微分方程的解即为1-AGO 序列的预测序列，如式(12)所示。将1-AGO 的预测序列进行逐级累减即可得到如式(13)所示的GM(1,1)冲蚀磨损预测模型。

上述一般形式的GM(1,1)模型被广泛应用在化工、能源等领域，同时也暴露出了一些该模型的缺点，比如只适用于短期预测，难以克服自身固有偏差等问题[30]。故需要对一般GM(1,1)模型做出优化。

2.1.2 无偏GM(1,1)冲蚀速率预测模型

针对一般形式的GM(1,1)模型所出现的长期预测精确度差和此类有偏的指数模型无法消除偏差问题，对系统发展系数a与GM(1,1)模型的并净值b通过式(14)、式(15)进行无偏估计修正[31]。

则弯管的冲蚀速率预测无偏灰色GM(1,1)模型为如式(16)。

在理论层面上相较于一般形式GM(1,1)模型，无偏GM(1,1)预测模型克服了一般GM(1,1)预测模型的固有偏差缺陷，比一般形式GM(1,1)预测模型有更广泛的应用空间，而且无偏GM(1,1)模型基于原始数据序列预测，不需要对1-AOG 预测序列的累减还原，简化了模型计算流程，提高了模型的计算效率[32]。

2.1.3 灰色马尔科夫预测模型

灰色马尔科夫模型以减小一般GM(1,1)模型预测结果与真实值之间误差作为修正为优化方向。灰色预测模型预测结果x^(0)(k+ 1)必定围绕真实值附近波动，灰色预测模型叠加马尔科夫模型即是对误差所处区间作出估计，缩小预测值与真实值之间的误差范围，使预测值在无限接近真实值的范围内波动，提高灰色预测模型的预测精度。灰色马尔科夫模型将灰色预测模型生成预测值的误差进行区间状态划分，将误差区间划分为E1、E2、…、En等n个状态子区间。依据马尔科夫链的无后效性质，i时刻状态只与i-1 时刻状态有关，不受之前预测值所产生的误差影响，经过对转化状态的统计，计算得到各个误差状态间的转移状态概率pij，而所有状态转移出现的频率所组成的矩阵即为步长为1 的马尔科夫状态转移概率矩阵，如式(17)所示。则从误差状态S经过一步转变为误差状态Si表示为Si=S×P。

因此，如果确定在Si时刻冲蚀磨损预测值的相对误差处于Ei区间内。则通过灰色马尔科夫预测模型对GM(1,1)模型所预测的冲蚀速率进行修正，修正后的预测值如式(18)。

2.2 预测模型精度分析

在以上3个预测模型建立后，需要对预测模型的精度与可信程度进行检验[33]，主要方式是对以上3个模型使用后验误差检验。后验误差比值C和小误差概率P计算如式(19)、式(20)所示，以P、C根据精度检验表（表1）所示的精度为衡量标准对以上预测模型做出评估。

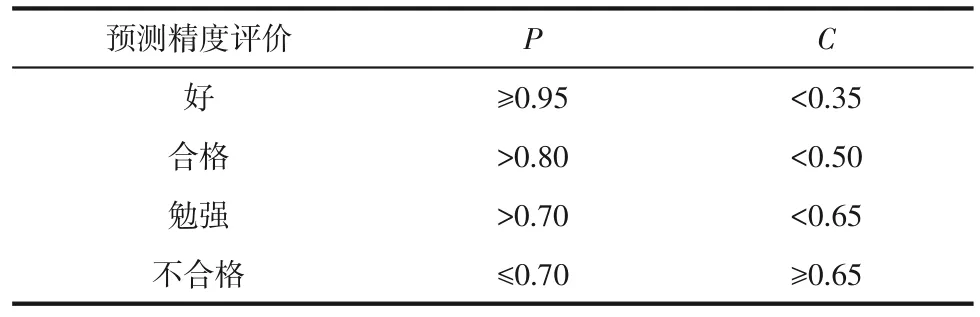
表1 精度检验表

式中，C为后验误差比值；P为小误差概率；s1为残差标准差；s2为原始数据标准差；εˉ为预测残差均值。

2.3 预测结果分析

以新疆某煤化工企业煤浆气化炉进料输送弯管的数值模拟为预测建模的原始序列。如表2 所示，以30天为1个数据采集周期在360天时间内共采集12 组生成预测的原始数据序列，用以替代在实际生产过程对冲蚀磨损减薄量的检测数据收集。

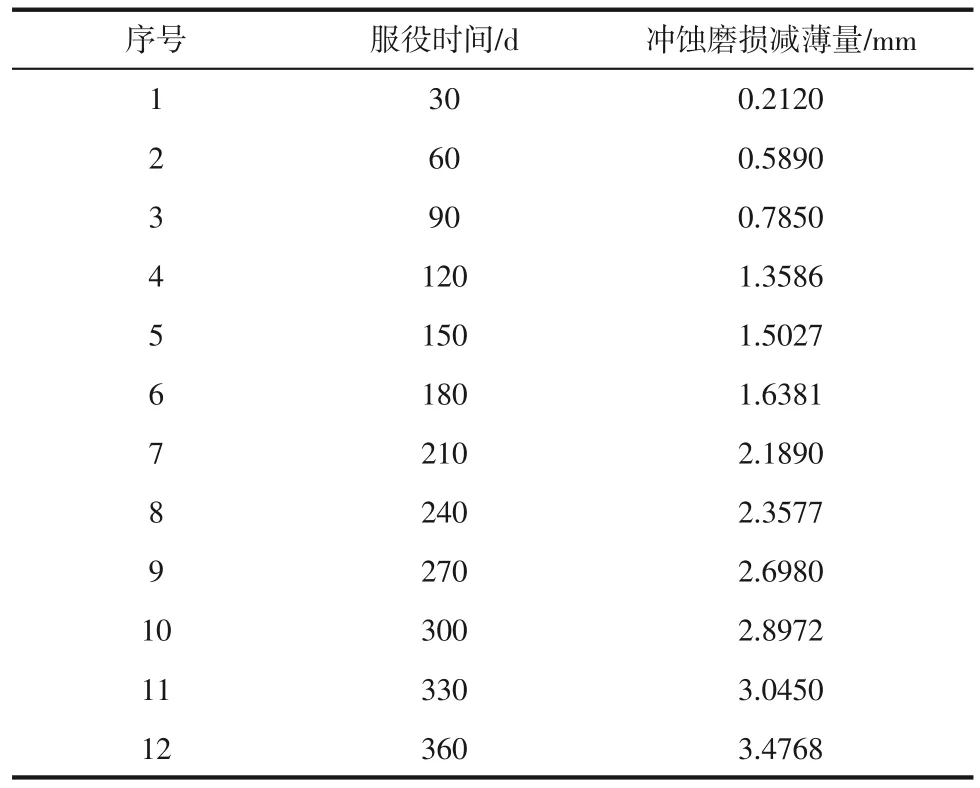
表2 减薄量数值模拟结果

借助MATLAB 2021b 软件对GM(1,1)预测模型与无偏GM(1,1)预测模型的系统发展系数、并净值以及无偏估计参数进行计算，结果为a=0.006，b=5.937，α=0.975，β=0.131。以表2内12组冲蚀减薄数据为原始数据进行预测，两种预测模型的预测结果位于表3 内。其中一般GM(1,1)模型与改进后的无偏GM(1,1)模型预测小误差概率P分别为0.833和1，后验误差比值C为0.144 和0.095。故根据精度检验表（表1）可知，一般GM(1,1)模型预测精度合格而无偏GM(1,1)预测精度为好，均可在一定精度范围内对冲蚀磨损减薄量做出预测。

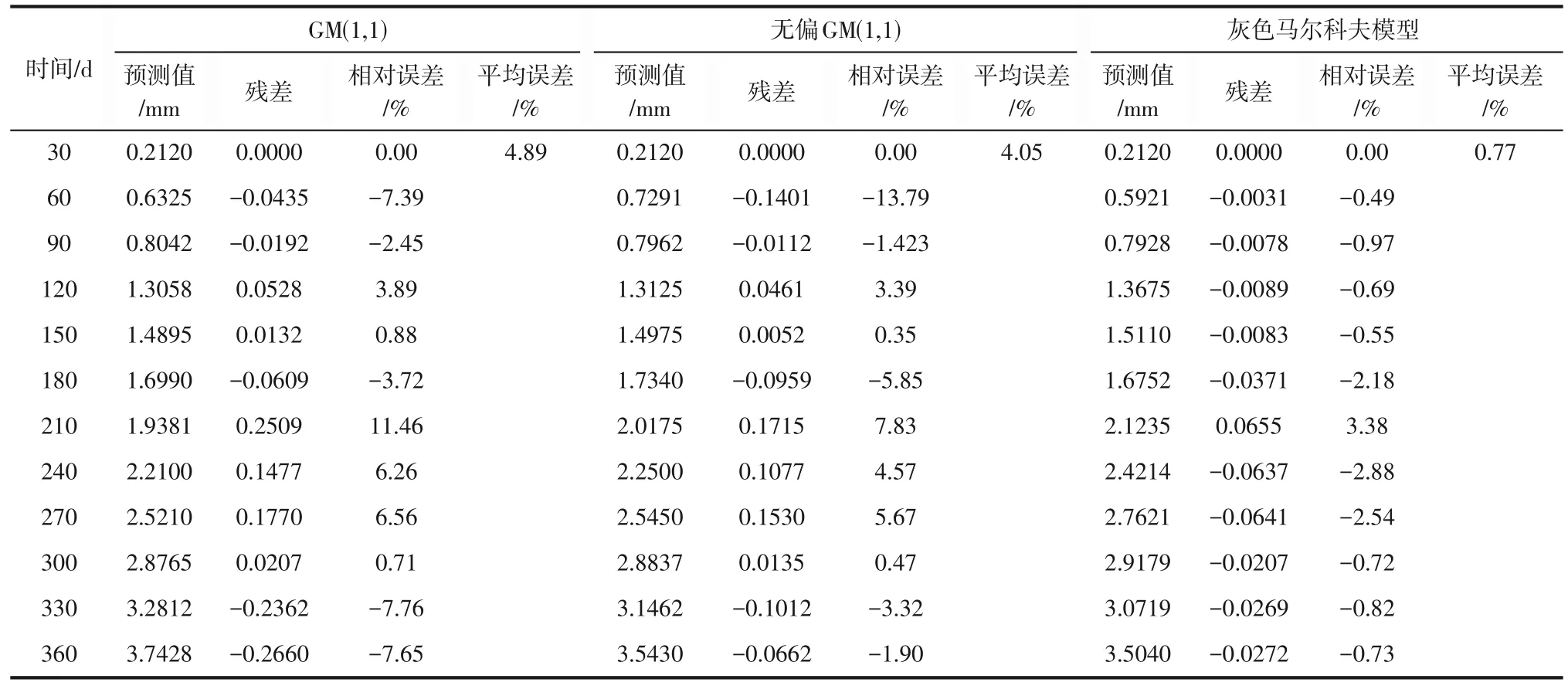
表3 不同预测模型结果对比

GM(1,1)预测模型相对误差区间为[-3.30, 7.87]，其序列均值u=3.47，标准差s=3.89，根据马尔科夫模型构建原理，故综合均值与方差将误差区间划分为如表4所示的4种误差状态。

表4 误差状态区间划分

根据表4 中的误差评价标准将GM(1,1)模型预测值根据误差所处区间进行状态划分（表5），且当预测值高于表5 中的模拟值时误差符号取正号，低于模拟值时误差符号取负号。统计表5中误差转移状态，得转移概率矩阵P如式(21)。

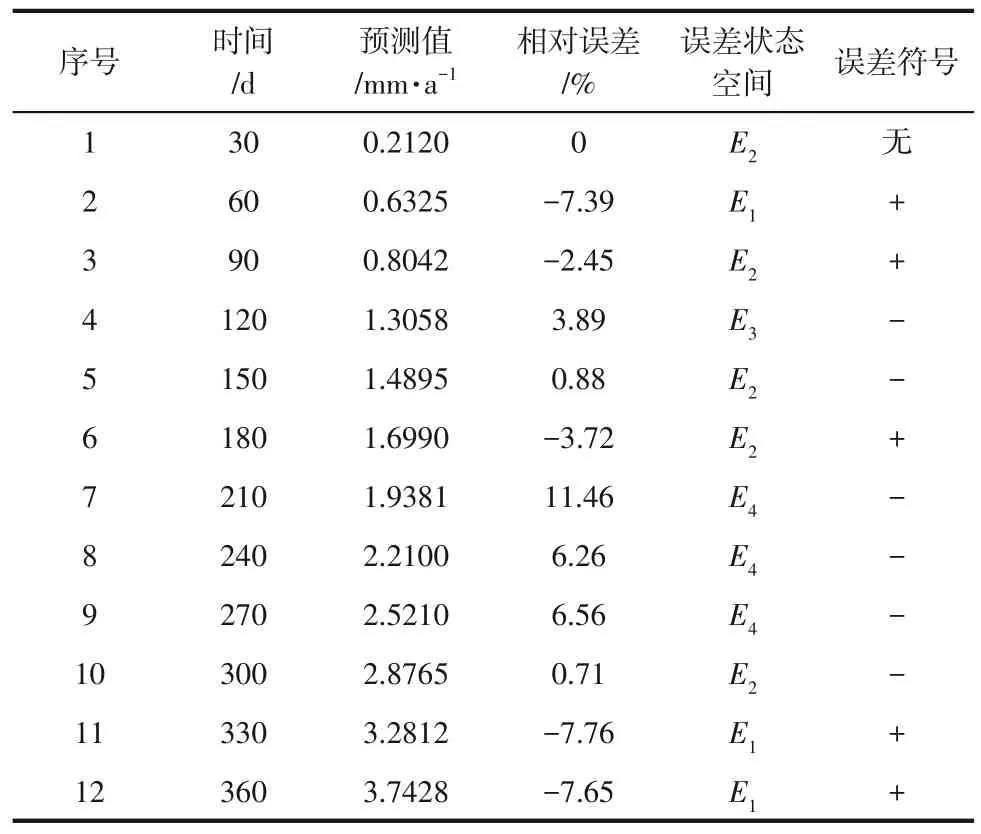
表5 GM(1,1)模型预测值与误差状态划分

以表5中第2组为例，其所处的空间状态为E1，并且预测值大于模拟值，根据式(18)对GM(1,1)模型预测值的误差修正结果如式(22)所示，其余具体计算结果列于表3中。灰色马尔科夫模型对于空间状态的预测一方面是根据GM(1,1)模型结果预测当前误差状态，另一方面可以获取预测值当前的误差符号用于修正误差。因此马尔科夫模型除对GM(1,1)模型当前误差进行修正外，还需对下一步预测值所处误差空间做出估计。以表5中第12组数据向后估计误差区间为例，第12 组所处误差状态由空间向量表示为E=[1 0 0 0]，下一步预测值所处误差状态应为E·P，因此第13 组预测值的误差区间处于E1的概率最大。以此类推，360天后的部分误差区间状态经计算后结果见表6。

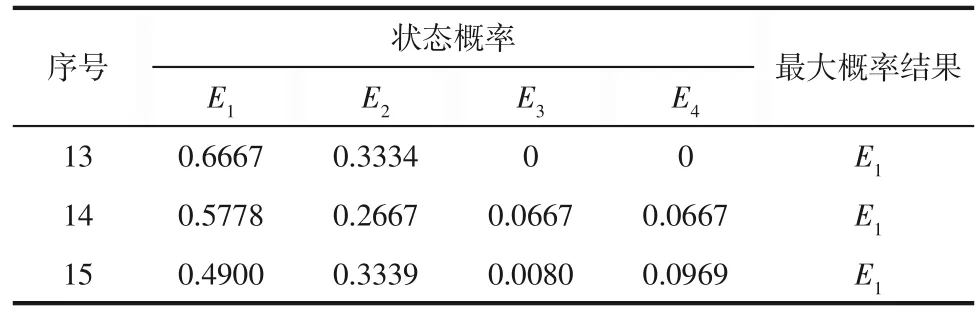
表6 空间状态预测结果

从表3可以看出，一般GM(1,1)模型预测值的平均相对误差是4.89%，进行无偏优化后的GM(1,1)模型预测值的平均误差为4.05%，比优化前预测精度提高了17.12%，无偏GM(1,1)模型预测精度比一般GM(1,1)模型已经大幅提高，但某些单点位置仍然存在较大的预测误差。在引入马尔科夫模型对误差进行优化后，预测值的平均误差降至0.77%，相较于一般GM(1,1)模型与无偏GM(1,1)模型的预测值，预测精度提升明显，分别提高了84%和80%。

由图7与图8更直观地看出GM(1,1)预测模型与无偏GM(1,1)预测模型在与初始值临近的短期预测区间内，与原始序列相比展现出良好的一致性，但随着预测时间增长都出现了误差逐渐增大现象。灰色马尔科夫模型与原始序列从始至终一致性都非常优秀，可见引入马尔科夫模型修正误差是解决GM(1,1)模型中长期预测不精确的有效手段。

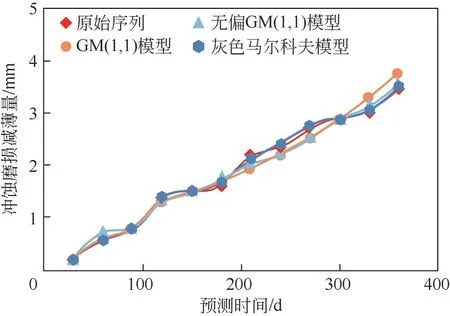
图7 不同模型预测值对比

图8 不同模型相对误差对比

3 管道寿命预测

根据我国石油天然气行业标准SY/T 6115—2009《钢质管道管体腐蚀损伤评价方法》，可将管道最大的冲蚀磨损减薄量作为管道寿命的评价标准并根据以往研究经验将在役管道局部损伤划分为5个服役状态[34-35]，其状态与冲蚀磨损最大减薄量对应关系见表7。

表7 管体冲蚀状态损伤评价划分

该企业水煤浆汽化炉进料弯管规格为DN100mm，公称壁厚h为12mm。根据上文所建立的灰色马尔科夫预测模型对冲蚀磨损减薄量以30天为一周期，使用MATLAB 2021b软件进行长期预测计算，预测计算程序至冲蚀减薄量预测值接近公称壁厚后结束，并依据表7所示的服役状态划分标准对管道服役状态进行划分（图9）。

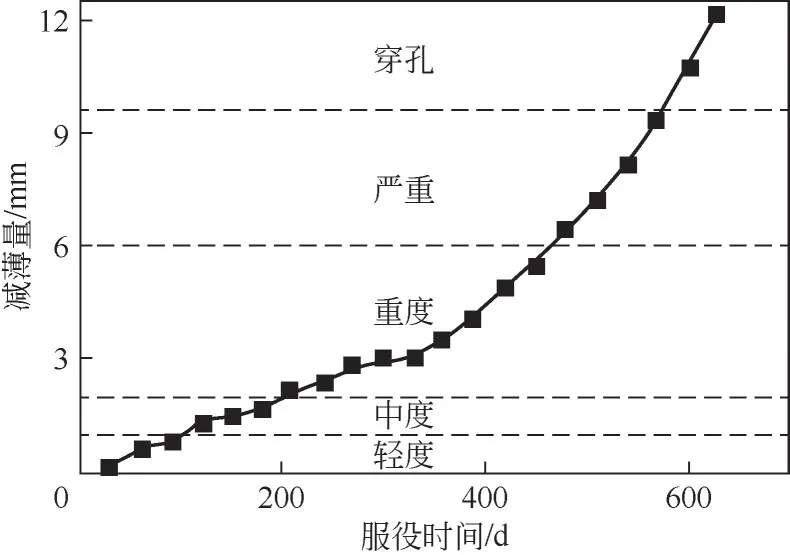
图9 服役状态与服役时间对应关系

如图9所示，该弯管在整个寿命周期中，较短时间内跨越了轻度与中度冲蚀磨损状态，服役期间的主要状态停留在重度与严重冲蚀磨损状态，自210天开始近11个预测周期停留在重度冲蚀磨损状态，冲蚀磨损减薄增长率较为平缓，超过450天后冲蚀磨损减薄量快速发展，管道服役状态由重度冲蚀转变为穿孔状态的过渡时间仅为120天。为确保管道系统的正常服役与煤化工设备安全，应在管道服役超过450天时对弯管关键点开展检修工作。

4 工程应用

该企业采纳以上研究成果后，将汽化炉两条分布在对称位置的进料管道的维修更换周期由360天更改为450 天，目前对预测效果共进行了为期3 个检修周期的验证，并对3个周期所更换下的6个弯头进行纵剖、除锈后测量得到表8所示的数据，其中1#、2#、5#为同一条进料管更换下的弯头，3#、4#、6#为对称侧进料管更换下的弯头。

表8 450天管道实测数据

表8 展示了6 个弯头在450 天时最大冲蚀减薄量实测值与最大减薄量预测值（值为5.6mm）的对比，预测值最大相对误差为6.42%，满足精度要求，基本验证了预测模型的准确性。弯管检修周期的延长，在一定程度上降低了检修的保守程度，减少了停工检修或切换备用设备的频率，极大提高了生产效率，压缩了生产成本。

5 结论

（1）数值模拟表明，固液两相流输送管道的最大冲蚀磨损部位不随时间变化发生移动现象，冲蚀减薄最大值主要集中在弯管轴向70°附近，该部位即为受冲蚀磨损管道的最危险点。

（2）无偏GM(1,1)预测模型与灰色马尔科夫模型两种优化后的模型预测精度比GM(1,1)预测模型均有提升，其中无偏GM(1,1)模型预测精度提升仅为17.12%，预测效果仍然不佳，而灰色马尔科夫模型将预测值相对误差降低到0.77%，预测效果明显优于其他两种预测模型。

（3）研究中所涉及的水煤浆气化炉进料弯管的服役寿命经初步预测仅为570天，且由正常服役状态向穿孔转变过渡时间短，为保证设备的安全运行，服役时间超过450天便需要对弯管最危险点进行重点检测工作。为便于管道运维人员开展快速预测计算与判断，将图9进行多项式拟合，得到服役时间与壁厚减薄量关系为ht=-0.2671+1.665×10-2t-4.325×10-5t2+7.6859×10-8t3。

符号说明

Aface——壁面单位表面积，m2

a——GM(1,1)模型系统发展系数

b——GM(1,1)模型并净值

b(v)——相对速度，m/s

C——后验误差

C(d

p)——颗粒直径系数

dp——颗粒直径，m

E——初始状态向量

Ei——第i个误差子区间

F——附加质量力，N

f(α)——颗粒碰撞角函数

Gk——平均速度梯度的湍流动能

Gb——浮力湍流动能

h——管道公称壁厚，mm

ht——t时刻壁厚减薄量，mm

k——湍流动能，J

LA，LB——上、下游直管长度，mm

mp——颗粒单位质量流率，kg/s

P——小误差概率

P——状态转移矩阵向量

RE——冲蚀速率，kg/(m2·s)

Sk，Sε——源项

t——管道服役时间

u，up——连续相与分散相速度，m/s

——预测原始序列

X(0)——一次累加序列

(k)——预测模型预测值

(k)——灰色马尔科夫模型修正后的预测值

YM——压缩流体湍流耗散

α，β——无偏GM(1,1)模型系数

ε——湍流耗散率，W/m3

γ——GM(1,1)模型背景系数

μ——连续相黏度，Pa·s

ρp、ρ——连续相与分散相密度，kg/m3