大数据融合在空气质量预测领域的应用
钱坤 张克凡


[摘 要] 大数据融合是将多种数据来源中的数据进行统一提取、融合,形成一个合适的数据集。以大数据的视角,运用大数据相关理论对传统问题进行研究,更能把握事物发展背后的规律,为决策提供支持。在通信领域,空气质量对信号传播效率和强度,以及通信计算服务器运行环境均有不可忽视的影响。本文研究宁波市每日的空气质量指数AQI以及六类主要污染物数据,运用大数据分析理论,对宁波空气质量进行分析预测,并挑选出最适合宁波的空气质量预测模型,预测出未来5天宁波的空气质量指数。
[关键词] 大数据分析;空气质量;通信;SARIMA;LSTM
doi : 10 . 3969 / j . issn . 1673 - 0194. 2023. 11. 051
[中图分类号] TP315 [文献标识码] A [文章编号] 1673 - 0194(2023)11- 0178- 05
0 引 言
如今,大数据理念和技术的普及程度呈持续上升的趋势,国务院发布的《“十四五”数字经济发展规划》指出,“数据要素是数字经济的核心引擎”。空气质量不仅在环境保护领域占据重要的地位,同时对经济发展也有重要的影响,例如在空气质量长期较差的情况下,居民相关疾病发病率会上升,在一定程度上阻碍经济发展。在通信领域,空气质量同样是重要影响因素:当雾霾较严重时,由于空气中颗粒物浓度较高,波的衍射现象发生的概率随之上升,信号的传播方向就更容易发生改变。此外,由于空气中介质浓度较高,信号强度通过介质时衰减程度较高,对日常生产生活也产生了消极影响。
宁波作为长三角城市圈内的重要城市,其经济与社会地位举足轻重。在大数据融合的背景下,建立相应的数理统计模型,对宁波市空气质量进行分析预测,研究其空气质量变化的背后原因及规律,不仅能够在环境保护方面提供建议,而且有助于规划城市发展道路,优化经济发展政策。
空气质量指数(AQI)是对当地空气质量的描述,是根据 PM2.5、PM10、NO2、CO、SO2 和 O3 等六个空气质量指标的浓度计算得到的。其计算公式如下:
式中:I为空气质量指数 AQI,Ih和It分别为 AQI 值上下限,Ch和Ct分别为污染物浓度上下限,C为该污染物当前浓度。空气质量指数 AQI 的取值等于上述六种污染物计算出的 6个I值的最大值。
本文选取2014年1月1日至2022年8月25日宁波市每日的空气质量指数AQI以及六类主要污染物数据。首先对其进行数据预处理,若数据存在缺失值,则需要通过相应算法进行插补。其次,文章通过相关性分析研究各指标之间的关联,并利用SARIMA模型与LSTM模型对宁波市未来空气质量指数进行预测,筛选出最优模型。
在进行SARIMA模型定阶时,与传统的利用ACF与PACF图不同,文章将网格搜索法引入SARIMA模型中,设定SARIMA模型的6个参数的最大值,通过网格搜索,依据AIC准则自动求得最优参数,节省时间的同时提高了模型预测的准确度。在拟合LSTM模型时,本文利用Adam算法优化替代了传统的参数寻找模式,提升了模型运行效率和准确性。
1 数据来源及方法介绍
1.1 数据来源
宁波是长三角城市圈内的重要城市,其经济与社会地位举足轻重。空气质量是影响城市发展的重要指标,研究并预测未来宁波的空气质量指数有重大现实意义。本文选取2014年1月1日至2022年8月25日宁波市每日的空气质量指数AQI以及六类主要污染物:PM2.5、PM10、SO2、CO、NO2 和 O3 的浓度数据(单位:μg/m3)。所有数据均摘自空气质量在线分析平台(www.aqistudy.cn)。
1.2 相關性分析
相关性分析是判断变量之间的相关程度,由相关系数进行衡量:相关系数值在0.8~1之间时,变量极强相关;相关系数值在0.6~0.8时,变量强相关;相关系数值在0.4~0.6时,变量中等强度相关;相关系数值在0.2~0.4时,变量弱相关;相关系数值在0~0.2时,变量极弱相关或不相关。
两变量X与Y之间的相关系数ρXY计算公式如下:
式中cov(X,Y)为变量X与变量Y之间的协方差,σX和σY分别为变量X与变量Y的标准差,μX和μY分别为变量X与变量Y的均值。
1.3 SARIMA模型
SARIMA模型由基础的ARIMA模型衍生而来,是在原有的ARIMA模型中增加季节参数得到。SARIMA的一般形式如下:
Φp(L)Ap(Ls)ΔdΔsDyt=Θq(L)BQ(Ls)εt(3)
其中yt为当前数据,εt为当前误差,(P,Q,p,q)分别为季节与非季节AR和MA参数,(D,d)分别表示季节和非季节性差分次数。在本研究中,将分别把yt定义为六类主要污染物浓度的取值。
1.4 LSTM模型
LSTM是一种自循环的神经网络,能够将之前学习到的参数权重引入下一次的学习中,并进行优化。 LSTM由一系列LSTM单元组成,其结构如图1所示。
2 数据预处理
本文采用的宁波 2014 年 1 月 1 日至 2022 年 8 月 25 日的空气质量指数(AQI)及各污染物浓度的数据是从空气质量在线分析平台(www.aqistudy.cn)摘录所得,其每日 AQI及各种污染物的浓度数据是根据当天宁波市内 9 个气象观测点观测的每小时实际数据,经过计算并对其求平均值所得,所以既存在数据观测记录时数据丢失,也存在计算过程中选取的算法导致数据缺失的情况。因此,在对数据进行分析前,必须检测数据是否完整,若存在缺失值,必须使用相应方法对其进行插补。由于本文数据集中各指标之间可能存在较强的线性关系,文章利用mice函数对数据进行数据缺失值的检测与插补,检测结果如图2所示。根据图2结果,数据集不存在缺失值,可以进行下一步分析。
3 基本数据分析
3.1 相关性分析
文章根据变量两两之间的相关系数,作出宁波空气质量的各指标相关系数图,结果如图3所示。通过分析各指标之间的相关系数可以提前找出各指标之间的关联,并有针对性地在之后的研究分析中着重讨论该部分。根据图3数据可以看出,空气质量指数AQI与O3的相关系数为0.32,说明AQI与该类主要污染物有一定的相关性,但相关性不强,属于弱相关;AQI与其余五类污染物相关性更低,因此可认为与其不相关。此外,SO2与CO的相关系数达到了0.51,属于中等强度相关,因此该两类污染物的变化很可能是同步的。
4 空气质量预测
对城市未来空气质量指数预测有相当重要的现实意义,根据预测结果,若当地空气质量指数在未来一段时间内呈持续下降趋势,则相关部门机构需要制定相应对策,来应对空气质量的变化。预测未来空气质量,能够为决策部门提供相应的建议。
本文聚焦2014年1月1日至2022年8月25日的空气质量指数AQI这一指标,将其构建为时间序列,对其分别建立SARIMA模型与LSTM模型,预测其未来的变化,并挑选出准确率更高、稳定性更强的模型。
4.1 SARIMA模型
SARIMA模型是在非季节的ARIMA(p,d,q)模型中加入了时间参数,构建了SARIMA(p,d,q)(P,D,Q)[T]模型,其中(P,D,Q)为季节参数,T为时间序列的周期。构建2014年1月1日至2022年8月25日的宁波市空气质量指数AQI的时间序列后,需对其进行季节性分解,判断其是否存在季节性,若存在,则需建立SARIMA模型,若不存在,建立ARIMA模型即可,季节性分解结果如图4所示。图4中seasonal图展示的是该时间序列的季节性趋势,从结果可以看出,宁波市空气质量指数AQI存在较强的季节性,而且大致以12月为周期,因此令参数T=12。trend图体现了时间序列的趋势性,若序列存在趋势性,则需要对其进行差分运算,使数据平稳化。从图中结果可看出,数据大致存在递减的趋势,为确定序列平稳性,还需对其进行ADF检验。经ADF检验后,其统计量p值为0.00,小于显著性水平0.05的阈值,因此序列是平稳的,无须对其进行差分运算,模型参数d为0。
由于SARIMA模型存在6个参数,若通过ACF和PACF图进行模型定阶效率低下,而且准确度较低。因此,本文选择通过网格搜索法,基于AIC和BIC准则,让模型自动搜寻参数,进行模型的定阶。在本研究中,选取参数(p,q)最大值为5,参数(P,Q)最大值为2,参数D值为1,利用网格搜索法和AIC、BIC准则进行模型定阶,得到最优SARIMA模型为SARIMA(3,0,3)(1,1,1)。本文将前80%数据设置为训练集,后20%数据设置为测试集,检验该模型在测试集上的预测情况,其结果如图5所示。从图中可以看出,该模型的预测值与真实值较为相似,因此可以作为宁波市空气质量指数AQI的预测模型。对未来5日的宁波市AQI进行预测,其结果如表1所示。
4.2 LSTM模型
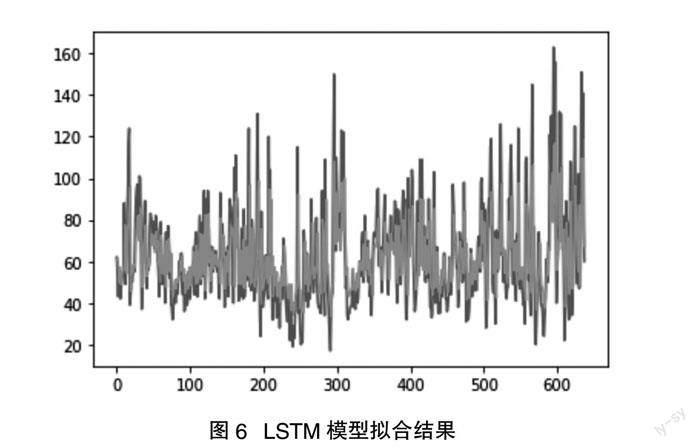
在使用SARIMA模型对宁波市空气质量指数AQI进行预测之后,为选取合适的预测模型,本文还利用LSTM模型对数据进行预测。与SARIMA建模过程相同,本文同样将前80%数据设置为训练集,将后20%数据设置为测试集,利用训练集数据拟合LSTM模型,并判断其在训练集上的预测准确度。由于LSTM模型中选取合适的参数较为困难,本文利用Adam算法对参数选取进行优化,自动计算出最优参数。经LSTM模型拟合,其在测试集上的预测值如图6所示。从图中结果可以看出,LSTM模型的预测值和真实值较为相似,而且相對于SARIMA模型,其对真实值的拟合程度更高,因此在预测宁波未来空气质量指数时,选用LSTM模型更为合适,对未来5天的空气质量指数进行预测,结果如表2所示。
5 结束语
经过对宁波市空气质量指数AQI以及其余六类污染物的分析,结果发现宁波市AQI与当地O3的相关性相较于其余五类污染物更大,因此其空气质量主要受当地O3浓度影响,但是其两者之间的相关性属于弱相关,因此还存在本文未研究的指标对空气质量产生了更大的影响。在空气质量预测阶段,本文选取了SARIMA模型,在原有ARIMA模型的基础上加入了季节性参数,增加了模型拟合和预测的准确性。此外,本文还选用了LSTM模型进行数据拟合,并与SARIMA模型进行对比,结果发现LSTM模型预测准确性更好,适合对宁波市未来的空气质量进行预测。在大数据的视角下对传统问题进行研究,能够更加准确、更加系统地对数据变化规律和原因进行探究把握,以数学的方式将问题发展的趋势一目了然地展现出来,为解决问题提供良好建议。同时,本文也存在一些不足之处,例如在研究各指标之间的关系时,仅仅使用了相关性分析,还没有进行更深层的研究,在时间序列预测时,也只使用了单变量时间序列预测,希望能在日后工作中继续深入探讨。
主要参考文献
[1]张冬雯,赵琪,许云峰,等.基于长短期记忆神经网络模型的空气质量预测[J].河北科技大学学报,2020(1):67-75.
[2]郑洋洋,白艳萍,续婷.基于SARIMA-SVR组合模型的空气质量指数预测[J].河北工业科技,2019,36(6):436-441.
[3]谢放尖,李文青,牟莹莹,等.宁波青奥期间污染减排对空气质量影响研究[J].环境科学与管理,2016,41(11):94-98.
[4]马丽娜,刘思强,陆小梅.定西市安定区手足口病SARIMA预测模型研究[J].中国公共卫生管理,2021,37(1):59-61.
[5]马明骏,赵海心,姜孝谟,等.基于LSTM-WPHM模型的风机轴承故障报警与寿命预测方法[J].风机技术,2022,64(3):63-71.

