基于社会压力敏感程度的观点动力学模型研究
张海波,陈 曦
(华中科技大学,武汉 430074)
0 引言
社会规范是指在特定情境下,被某一群体成员广泛认可的行为标准。当个体与舆论环境中其他个体交流时,会因为想要获得群体接受、实现社会成功及表明对一个群体的归属感等动机而遵守社会规范。社会压力是指需要个体改变自己观点以符合社会规范的力量[1]。当个体感知到社会压力时,会产生改变其原有观点或行为的倾向。不同个体对社会压力的敏感程度存在差异,对压力敏感的个体更容易产生调整自己行为或观点的倾向,而对压力不敏感的个体更能够在压力中保持原有观点或行为。ledgerwood a认为,社会压力对不同个体的作用效果存在差异,这种作用效果与双方的心理抗压能力成正比[2]。thomson o’brien ma对社会压力的量化研究发现,意见领袖的存在能够加大社会压力对个体的影响程度[3]。朱常海认为,个体面对社会压力时会产生不安感[4],尤其是对社会压力敏感的个体,其更可能会调整自己的观点或行为。
个体在交流中的复杂行为是交叉学科研究的重要领域。研究者在研究舆论演化的过程中,会考虑到各种社会心理学因素造成的影响,如基于智能体建模方式构建的HK模型、DW模型、Sznajd[5]模型。有学者将量化后的社会压力引入到观点动力学的模型中。一些研究者把社会压力量化为整个社会的普遍观点给予个体的压力,其中Wu扩展了Degroot模型,在提出的模型中认为,个体更新观点时,会考虑个体原有观点、个体邻居的观点及社会所有个体平均观点的影响[6]。张轩宇针对偏见同化理论,对社会压力造成的舆论演化影响进行了探索,提出在外界意见与个体自身观点有差异时,个体会担心观点差距带来负面影响而改变自身的观点表达[7]。李妍洁认为,社会压力与个体和社会平均观点的差距呈正相关,并使用幂函数来描述二者间的关系[8]。综上,现有关于社会压力量化的研究还比较浅显,且普遍认为,社会上所有个体能够感知到的社会压力相同,社会压力能够直接改变个体的观点。
事实上,处于社会网络中的不同个体接收到的信息不同,感知到的社会压力也会存在差异。社会压力对个体的影响体现在能够增加个体改变观点的可能性。个体间一对一的交流会直接改变个体的观点,而社会压力会更容易让个体动摇,促进个体在下次交流时改变已有的观点。社会压力的特点是比较稳定,个体每次交流的对象可能会持有不同的观点,每一次交流获取到的观点会存在较大波动,而个体邻居中的支持者和反对者比例比较稳定,故社会压力变化相对较慢。本研究尝试引入邻居观点的稳定性作为社会压力的定量描述,在考虑个体敏感程度的基础上,基于DW模型,构建新的观点动力学模型,并通过数学推导分析社会压力敏感程度在观点演化中起的作用,探讨社会压力影响下舆论演化的规律。
1 模型构建
在DW模型的信任半径中,引入个体敏感系数m,构建新的观点动力学模型。个体邻居形成的群体规范会给予个体带来一定社会压力,具有不同压力敏感程度的个体感知到社会压力后,信任半径出现不同程度的增加,决定了个体在下一次交流中是否会考虑对方的观点。引入信任半径变化过程到传统DW模型中,并修改DW模型中双方同时更新观点的机制,使双方观点独立更新,互不影响,进而提出建构一个信任半径异质且动态变化的有界置信模型。
社会压力的强度与两个因素有关:当环境的均值与个体的观点接近时,个体认为自己的观点与主流观点相吻合,感知到的社会压力较小。当环境的均值与个体的观点相差较远时,个体认为自己的观点偏离了主流观点,感知到的社会压力则较大。环境的声音是否一致也会影响个体社会压力的大小,观点异质的环境会增大这种压力,观点混乱的群体会减小这种压力。模型中,将个体i感知到的社会压力定义为:
(1)
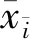
DW模型是用于描述个体间一对一交流的有界置信模型,模型中的个体把自己观点附近的区域称为信任域,只有当对方的观点在个体的信任域内时,个体才会把对方当成可以交流的邻居。经典的DW模型规则如下:系统中的个体分布在二维平面矩形网格中,每个个体对某一话题持有初始观点值,初始观点值是0~1上的某一随机实数,0为极端反对,1为极端赞成。在演化过程中,每个时刻随机选出一对格子内的相邻个体i和j,当两个个体观点差值小于某一阈值ε(信任半径),则分别根据公式(2)进行观点更新,如此循环执行,直至达到实验终止条件或舆论演化达到稳定状态。
(2)
式(2)中,w∈[0,1]是固执程度,w=0.5表示个体更新观点为双方观点的平均值。w=1表示个体极端固执,完全不接受对方的观点。0表示个体极端随和,完全接受对方的观点。传统DW模型中假设信任域固定不变,且忽略了其他邻居对个体的影响。邻居是个体感知社会压力的来源,不与个体直接交流的邻居虽然不会直接改变个体的观点,但会给个体施加潜在的压力,增加个体交流并改变观点的可能性。针对这种邻居传递的社会压力作用在个体身上的过程进行建模。经典的DW模型中,所有个体具有相同的信任半径,参与交流的双方会同时交流,而新建模型中个体具有不同的信任半径,双方是否交流是独立的。
舆论环境对个体施加社会压力,在社会压力的作用下,个体变得更加容易采纳新的观点,即扩大自己的信任半径。个体i的信任半径:
εi=mPi+ε0
(3)
式(3)中,m为个体的压力敏感系数,表示个体在单位环境压力作用下,信任半径增加的程度。ε0为个体的基础信任半径。结合公式(3),个体i的信任半径可以表示为公式(4)。个体i与其邻居个体j交流后,若对方的观点在自己的信任半径内,个体i和j就会根据公式(5)更新自己的观点。
(4)
(5)
式(5)中,w为个体的固执程度,即个体对自己已有观点的坚持程度。w值越大说明个体越固执,反之个体越随和。该模型中,个体持有的信任半径并非一成不变,而是随着个体所处的舆论环境变化而变化。不同舆论环境产生的社会压力强度不同,这种社会压力使得个体的信任半径增加的程度也不同。当网络中的个体持有极端观点时,会承受更大的压力,具有更大的信任域。当其持有中立观点时,承受的压力较小,则具有较小的信任域。当且仅当邻居观点的均值与自己观点相同时,个体感知到的环境压力为0,个体拥有最小的信任半径,即基础信任半径。
2 模型分析
经典的DW模型中,当个体的信任半径足够大时,群体能够达成共识。当信任半径较小时,随着观点交流的进行,个体邻居的观点逐渐统一,个体感知到的压力会逐渐增大,促使个体作出改变,整个群体可能会形成一个或多个观点簇,簇内个体观点相近,簇与簇间的观点相差较大。群体中的个体由于拥有足够多观点相似的邻居,感知到的社会压力较小,个体的信任域仅包含当前观点簇内的邻居,簇与簇间不再交流,整个群体达到稳定状态。个体压力敏感系数m是群体能否达成统一的关键因素,但需要进一步推导才能确定当m为何值时群体能够达到统一。
根据式(4)、式(5)定义的个体交流规则,个体压力敏感系数m对群体统一的形成具有以下影响:
定理1:在全连接网络中,当m>(1-0)时,群体必定能够达成观点统一。当[(1-0)/2] 为了证明定理1成立,将证明在m>(1-0)且群体观点数量簇大于1时,持有极端观点的个体始终能够找到邻居进行交流以减少自己观点的极端程度,增加群体观点的一致性,最终能够达到观点的统一。在m>[(1-0)/2]且群体观点簇数量大于2时,持有极端观点的个体始终能够找到邻居交流以减少自己观点的极端程度,增加群体观点的一致程度,最终能够达到观点的统一或形成两个独立的观点种群。 个体i能够与个体j进行交流的条件是个体i感知到的压力大于双方的观点差,即 (6) 故此个体i的信任半径内存在持有不同观点的个体的条件是 (7) (8) 用[x]表示一个不大于x的整数,当xp=0,xq=1,a=[n/2]时,式(8)右边取最大值m*,最大值m*为 (9) 若m>m*,可以保证无论a、b、xp、xq为何值,持有极端观点xp的个体i总能与持有不同观点(即xq)的个体j交流,并减少自己观点的极端程度。根据公式9可知,m*始终小于(1-0),当n趋于无穷时,m*=(1-0)。在全连接网络中,当m>(1-0)时,群体达到稳定时包含的观点簇数量不可能为2或群体必定能够最终达到统一。当[(1-0)/2] 先分析了社会压力对个体观点改变的促进作用,又把社会压力引入观点动力学,提出了一种考虑个体对社会压力敏感程度的观点动力学模型。在这个模型中,社会压力使个体信任半径增大,使个体在下次更新自己观点时,更容易接受他人的观点。对模型进行分析发现,全连接网络中,社会压力敏感系数足够大时,群体必定能够达到观点的统一,有助于深入理解社会压力对观点统一和极化的影响,为相关领域学者提供关于社会压力研究的新思路。对模型进行数学推导发现,在全连接网络中,不论群体观点初始值如何分布,当所有个体均具有大于1的压力敏感系数时,群体必定能够达到统一。对舆论治理者来说,为了促进群体意见达成一致,可以设法增加群体中所有个体的压力敏感程度,以此加快个体的交流频率,促进群体达成共识。
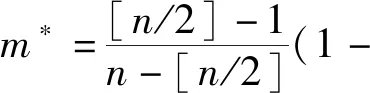
3 研究结论

