2023年新高考数学Ⅰ卷亮点试题评析

【摘 要】  2023年新高考数学Ⅰ卷试题命制情境新颖，设问、表述清新、简约，是一份深受好評的数学试卷.经过对2023年新高考数学Ⅰ卷中出现的一些亮点试题的认真研究，从中看出新高考数学Ⅰ卷促进学生提高学科素养的命题导向引领高考备考.

【关键词】  2023年；新高考Ⅰ卷；亮点试题；评析

2023年新高考数学Ⅰ卷落实基础性与综合性的考查要求，聚焦数学核心素养，精选试题情境，出现了一些表述简洁、背景鲜活、情境新颖的亮点试题.下面就这些亮点试题进行评析，供参考.

1   单选亮点题

例1  （第4题）设函数f（x）=2x（x-a）在区间（0，1）上单调递减，则a的取值范围是（  ）.

A.（-∞，-2］    B.［-2，0）C.（0，2］    D.［2，+∞）

分析  由指数型复合函数单调性，根据“同增异减”规律，转化为二次函数的单调性列式计算作答.

解   因为函数y=2x在 R 上单调递增，而函数f（x）=2x（x-a）在区间（0，1）上单调递减，则函数y=x（x-a）=x2-ax= x- a 2  2- a2 4 在区间（0，1）上单调递减，所以 a 2 ≥1，解得a≥2，所以a的取值范围是［2，+∞）.故选D.

评析  试题落实高考命题“基础性”和“全面性”考查要求，考查考生对基础知识和基本方法的深刻理解和融会贯通的应用.将复合函数的单调性转化为二次函数的单调性，考查化归转化思想的运用.试题亮点在于巧妙地用单调性考查了二次函数的知识.  例2  （第7题）记Sn为数列{an}的前n项和，设甲：{an}为等差数列；乙：  Sn n  为等差数列，则（  ）.

A.甲是乙的充分条件但不是必要条件

B.甲是乙的必要条件但不是充分条件

C.甲是乙的充要条件

D.甲既不是乙的充分条件也不是乙的必要条件

分析  根据充分条件、必要条件的定义及等差数列的定义，并结合等差数列前n项和公式以及数列前n项和与第n项的关系作出推理判断. 解  首先判断充分性.

因为甲：{an}为等差数列，设其公差为d，所以Sn=na1+ n（n-1） 2 d，所以 Sn n =a1+ n-1 2 d，所以 Sn+1 n+1 - Sn n = a1+ n 2 d - a1+ n-1 2 d = 1 2 d，由数列定义知  Sn n  为等差数列，则甲是乙的充分条件，充分性成立.再来判断必要性.

因为乙：  Sn n  为等差数列，由等差数列定义知 Sn+1 n+1 - Sn n 为常数，设为d′（常数），所以 Sn n = S1 1 +（n-1）d′=S1+（n-1）d′，所以Sn=nS1+n（n-1）d′.

于是，当n≥2时，an=Sn-Sn-1=nS1+n（n-1）d′-（n-1）S1-（n-1）（n-2）d′=S1+2（n-1）d′，所以an-an-1=S1+2（n-1）d′-S1-2（n-2）d′=2d′为常数，所以{an}为等差数列，则甲是乙的必要条件，必要性成立.

故选C.

评析   试题以等差数列有关知识的应用为情境，考查充要条件的推理论证，要求考生判断充分性和必要性，然后分别进行证明，解决问题的关键是利用等差数列的概念和特点进行推理论证，彰显了对数学运算、逻辑推理等核心素养的考查.试题亮点在于以等差数列情境考查充要条件的推理论证.  2   多选亮点题

例3  （第9题）有一组样本数据x1，x2，…，x6，其中x1是最小值，x6是最大值，则（  ）.

A.x2，x3，x4，x5的平均数等于x1，x2，…，x6的平均数

B.x2，x3，x4，x5的中位数等于x1，x2，…，x6的中位数

C.x2，x3，x4，x5的标准差不小于x1，x2，…，x6的标准差

D.x2，x3，x4，x5的极差不大于x1，x2，…，x6的极差

分析  依据题意，应用平均数、中位数、标准差及极差等数字特征的概念逐项分析作出判断.

解  对于A，如设2，2，2，2的平均数为2；1，2，2，2，2，9的平均数为3，故A错误.

对于B，不妨设x1≤x2≤x3≤x4≤x5≤x6，可知x2，x3，x4，x5的中位数等于x1，x2，…，x6的中位数均为 x3+x4 2 ，故B正确.

对于C，因为x1是最小值，x6是最大值，则x2，x3，x4，x5的波动性不大于x1，x2，…，x6的波动性，即x2，x3，x4，x5的标准差不大于x1，x2，…，x6的标准差，故C错误.

对于D，不妨设x1≤x2≤x3≤x4≤x5≤x6，则x6-x1≥x5-x2，当且仅当x1=x2，x5=x6时，等号成立，故D正确.综上，选BD.

评析  试题考查统计抽样中样本的基本数字特征，考查考生对样本平均数、样本标准差、样本中位数、样本极差概念的理解和掌握，不仅注重试题的基础性，而且对基础知识和基本能力的考查有机结合.试题亮点是：以清新的设问情境，很好地考查了统计中的平均数、中位数、方差、极差等数字特征的理解和知识应用.

例4  （第10题）噪声污染问题越来越受到重视．用声压级来度量声音的强弱，定义声压级Lp=20×lg p p0 ，其中常数p0（p0>0）是听觉下限阈值，p是实际声压.下表为不同声源的声压级：

声源 与声源的距离/m 声压级/dB

燃油汽车 10 60～90

混合动力汽车 10 50～60

电动汽车 10 40

已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为p1，p2，p3，则（  ）.

A.p1≥p2    B.p2>10p3

C.p3=100p0 D.p1≤100p2

分析  根据题意可知Lp1∈［60，90］，Lp2∈［50，60］，Lp3=40，结合对数运算逐项分析判断.

解  根据题意可知：Lp1∈［60，90］，Lp2∈［50，60］，Lp3=40.

对于A，Lp1-Lp2=20×lg p1 p0 -20×lg p2 p0 =20×lg  p1 p0 × p0 p2  =20×lg p1 p2 .由Lp1≥Lp2，得Lp1-Lp2=20×lg p1 p2 ≥0，lg p1 p2 ≥0，即 p1 p2 ≥1且p1，p2>0，所以p1≥p2.A正确.

对于B，Lp2-Lp3=20×lg p2 p0 -20×lg p3 p0 =20×lg  p2 p0 × p0 p3  =20×lg p2 p3 .

由于Lp2-Lp3=Lp2-40≥10，因此20×lg p2 p3 ≥10，lg p2 p3 ≥ 1 2 ，即 p2 p3 ≥ 10 且p2，p3>0，所以得p2≥ 10 p3，当且仅当Lp2=50时，取到等号.B错误.

对于C，由于Lp3=20×lg p3 p0 =40，lg p3 p0 =2，所以 p3 p0 =100，所以p3=100p0. C正确.

对于D，根据A可知Lp1-Lp2=20×lg p1 p2 ，且Lp1-Lp2≤90-50=40，因此得20×lg p1 p2 ≤40，所以lg p1 p2 ≤2，即 p1 p2 ≤100，且p1，p2>0，所以p1≤100p2. D正确.

综上，选ACD.

评析  试题利用对数知识研究噪声声压水平，经过对声压级的研究，考查了对数及运算性质的应用，很好地考查考生对问题的理解和应用能力.表面上看试题题干精炼，但计算量较大，审题和计算都需要认真、仔细，稍有不慎，就会导致误解题意而耗费时间.试题亮点：源于人教A版《普通高中教科书.数学必修第一册》（2019版）第141页习题4.4第10题的“声强”问题，体现高考命题源于教材的原则. 例5  （第12题）下列物体，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（  ）.

A.直径为0.99 m的球体B.所有棱长均为1.4 m的四面体

C.底面直径为0.01 m，高为1.8 m的圆柱体

D.底面直径为1.2 m，高为0.01 m的圆柱体

分析  根据题意结合正方体的性质逐项分析判断.对于C、D，以正方体的体对角线为圆柱体的轴，结合正方体以及圆柱体的性质分析判断.

解  对于A，棱长为1（单位：m）的正方体内切球的直径为1m. A正确.

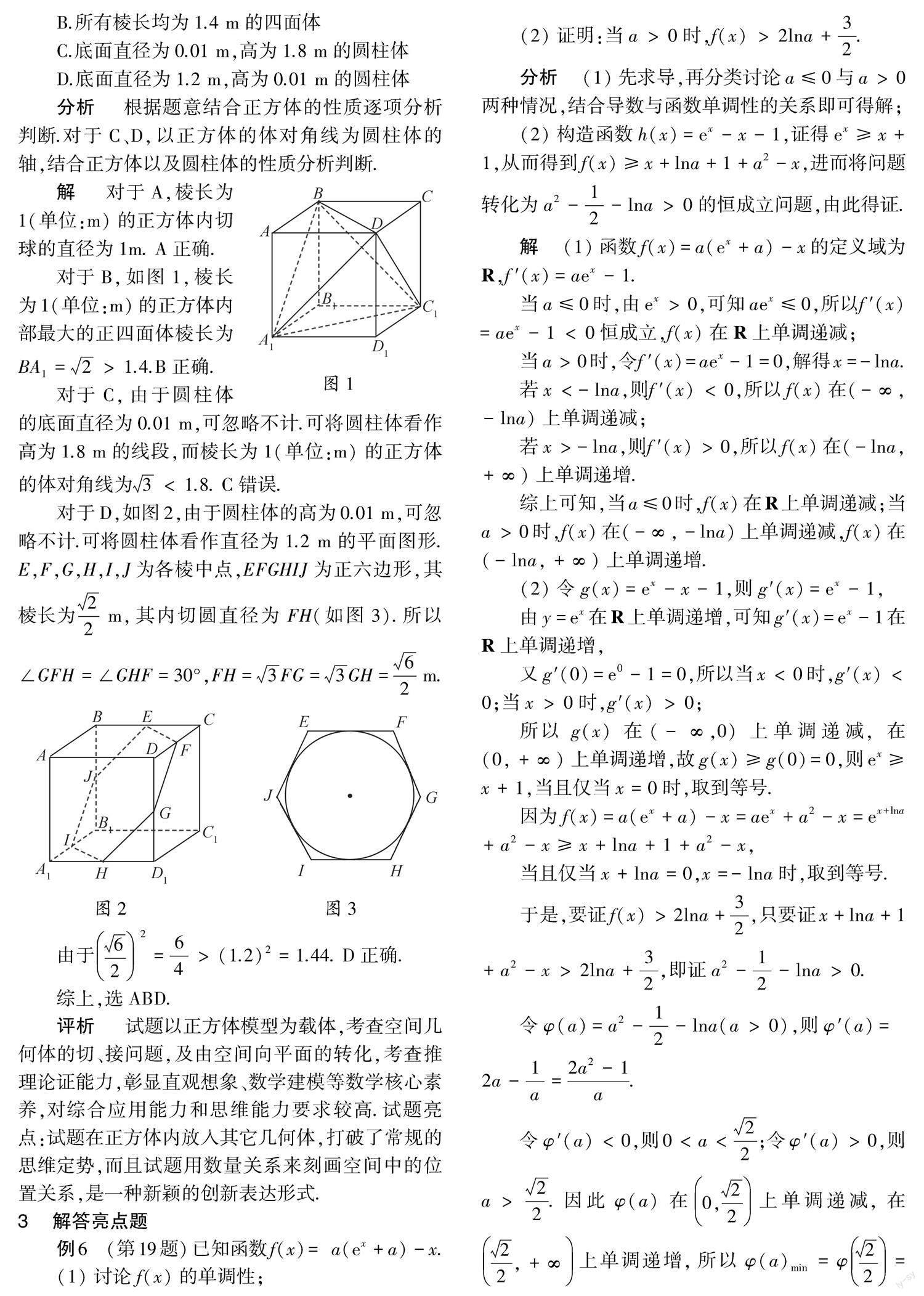
对于B，如图1，棱长为1（单位：m）的正方体内部最大的正四面体棱长为BA1= 2 >1.4.B正确.

对于C，由于圆柱体的底面直径为0.01 m，可忽略不计.可将圆柱体看作高为1.8 m的线段，而棱长为1（单位：m）的正方体的体对角线为 3 <1.8. C错误.

对于D，如图2，由于圆柱体的高为0.01 m，可忽略不计.可将圆柱體看作直径为1.2 m的平面图形. E，F，G，H，I，J为各棱中点，EFGHIJ为正六边形，其棱长为  2  2  m，其内切圆直径为FH（如图3）.所以∠GFH=∠GHF=30°，FH= 3 FG= 3 GH=  6  2  m.

由于   6  2  2= 6 4 >（1.2）2=1.44. D正确.

综上，选ABD.

评析   试题以正方体模型为载体，考查空间几何体的切、接问题，及由空间向平面的转化，考查推理论证能力，彰显直观想象、数学建模等数学核心素养，对综合应用能力和思维能力要求较高.试题亮点：试题在正方体内放入其它几何体，打破了常规的思维定势，而且试题用数量关系来刻画空间中的位置关系，是一种新颖的创新表达形式. 3   解答亮点题 例6  （第19题）已知函数f（x）=a（ex+a）-x.

（1）讨论f（x）的单调性；

（2）证明：当a>0时，f（x）>2lna+ 3 2 ．

分析  （1）先求导，再分类讨论a≤0与a>0两种情况，结合导数与函数单调性的关系即可得解；

（2）构造函数h（x）=ex-x-1，证得ex≥x+1，从而得到f（x）≥x+lna+1+a2-x，进而将问题转化为a2- 1 2 -lna>0的恒成立问题，由此得证.

解  （1）函数f（x）=a（ex+a）-x的定义域为 R ，f′（x）=aex-1.

当a≤0时，由ex>0，可知aex≤0，所以f′（x）=aex-1<0恒成立，f（x）在 R 上单调递减；

当a>0时，令f′（x）=aex-1=0，解得x=-lna.

若x<-lna，则f′（x）<0，所以f（x）在（-∞，-lna）上单调递减；

若x>-lna，则f′（x）>0，所以f（x）在（-lna，+∞）上单调递增.

综上可知，当a≤0时，f（x）在 R 上单调递减；当a>0时，f（x）在（-∞，-lna）上单调递减，f（x）在（-lna，+∞）上单调递增.

（2）令g（x）=ex-x-1，则g′（x）=ex-1，

由y=ex在 R 上单调递增，可知g′（x）=ex-1在 R 上单调递增，

又g′（0）=e0-1=0，所以当x<0时，g′（x）<0；当x>0时，g′（x）>0；

所以g（x）在（-∞，0）上单调递减，在（0，+∞）上单调递增，

故g（x）≥g（0）=0，则ex≥x+1，当且仅当x=0时，取到等号.

因为f（x）=a（ex+a）-x=aex+a2-x=ex+lna+a2-x≥x+lna+1+a2-x，

当且仅当x+lna=0，x=-lna时，取到等号.

于是，要证f（x）>2lna+ 3 2 ，只要证x+lna+1+a2-x>2lna+ 3 2 ，即证a2- 1 2 -lna>0.

令φ（a）=a2- 1 2 -lna（a>0），则φ′（a）=2a- 1 a = 2a2-1 a .

令φ′（a）<0，则00，则a>  2  2 .因此φ（a）在 0，  2  2  上单调递减，在   2  2 ，+∞ 上单调递增，所以φ（a）min=φ   2  2  =   2  2  2- 1 2 -ln  2  2 =ln 2 >0，从而有φ（a）>0恒成立.故当a>0时，f（x）>2lna+ 3 2 恒成立.证毕.

评析  试题以基本函数ex为背景命题，第（1）小题考查应用导数讨论函数的单调性；第（2）小题将不等式证明问题，通过构造函数，转化为不等式恒成立问题来解答.试题最大亮点在于打破了人们将导数应用的大题作为整个试卷“压轴题”的惯性认知，而是以“中档题”放置在第19题的位置，这既是整份试卷的最大变化，也是命题者“反刷题”“反押题”的独具匠心，对今后高考复习备考有着积极的导向作用.

例7  （第21题）甲乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮.无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为0.5.

（1）求第2次投篮的人是乙的概率；（2）求第i次投篮的人是甲的概率；

（3）已知：若随机变量xi服从两点分布，且P（xi=1）=1-P（xi=0）=qi，i=1，2，…，n，则E（∑ n i=1 xi）=∑ n i=1 qi.记前n次（即从第1次到第n次投篮）中甲投篮的次数为Y，求E（Y）.

分析  （1）根据全概率公式即可求出;

（2）设P（ai）=pi，由题意可得pi+1=0.4pi+0.2，根据数列知识，构造等比数列即可解出;

（3）先求出两点分布的期望，再根据题中的结论以及等比数列的求和公式即可求出．

解  （1）记“第i次投篮的人是甲”为事件Ai，“第i次投籃的人是乙”为事件Bi，

则P（B2）=P（A1B2）+P（B1B2）=P（A1）P（B2|A1）+P（B1）P（B2|B1）=0.5×（1-0.6）+0.5×0.8=0.6.

所以第2次投篮的人是乙的概率为0.6.

（2）设P（Ai）=pi，则根据题意可知P（Bi）=1-pi，所以

P（Ai+1）=P（AiAi+1）+P（BiAi+1）=P（Ai）P（Ai+1|Ai）+P（Bi）P（Ai+1|Bi），即pi+1=0.6pi+（1-0.8）×（1-pi）=0.4pi+0.2，从而得pi=0.4pi-1+0.2. ①

令pi+t=0.4（pi-1+t），所以pi=0.4pi-1-0.6t.  ②

故由①②，可得-0.6t=0.2，解得t=- 1 3 ，所以pi- 1 3 = 2 5  pi-1- 1 3  .

由p1=0.5= 1 2 ，得p1- 1 3 = 1 2 - 1 3 = 1 6 .

所以 pn- 1 3  是首项为 1 6 、公比为 2 5 的等比数列，所以pn- 1 3 = 1 6   2 5  n-1，即pn= 1 6   2 5  n-1+ 1 3 .

故第i次投篮的人是甲的概率为pi= 1 6 ·  2 5  i-1+ 1 3 .

（3）因为pi= 1 6 ·  2 5  i-1+ 1 3 ，i=1，2，…，n.所以当n∈ N *时，E（Y）=p1+p2+…+pn= 1 6 × 1-  2 5  n 1- 2 5  + n 3 = 5 18  1-  2 5  n + n 3 ，

故E（Y）= 5 18 · 1-  2 5  n + n 3 .

评析  试题是概率与递推数列融合、渗透的问题，第（1）小题考查了全概率公式的应用，第（2）（3）小题关键是由题意求得递推公式，然后根据等比数列的基本知识求解.对于这类问题，若直接求概率困难较大，而由问题特点建立关于概率的递推数列模型，利用递推的方法，再结合数列知识转化为求解数列通项公式及数列求和，可使问题得以顺利解决.试题亮点是：在概率中“隐藏”了等比数列的通项公式、求和公式等知识点，将概率与递推数列结合在一起考查.其实，这种命题方式在2019年全国Ⅰ卷理科的第21题就曾出现过，而且新教材《普通高中教科书·A版数学选择性必修第三册》（2019年版）第91页复习参考题7中的第10题（三人传球训练）是这类问题的教材原型.试题将递推数列与随机变量的概率分布及数学期望有机融合，则是一种全新的考法.

例8  （第22题）在直角坐标系xOy中，点P到x轴的距离等于点P到点 0， 1 2  的距离，记动点P的轨迹为W.

（1）求W的轨迹方程；

（2）已知矩形ABCD有三个顶点在W上，证明：矩形ABCD的周长大于3 3 .

分析  （1）设P（x，y），根据题意列出方程x2+ y－ 1 2  2=y2，化简即可；（2）设直线AB的方程为y=k（x-a）+a2+ 1 4 ，将其与抛物线方程联立，再利用弦长公式和放缩法得 AB + AD ≥  （1+k2）3 k2  ，利用换元法和求导即可求出周长最值，再排除邊界值即可.

解  （1）设点P（x，y），则由题意得 y = x2+ y- 1 2  2 ，化简、整理得y=x2+ 1 4 .

所以W的轨迹方程为y=x2+ 1 4 .

（2）不妨设A，B，D三点在W上，且BA⊥DA.

设A a，a2+ 1 4  ，直线BA，DA的斜率分别为k，- 1 k ，根据对称性不妨设|k|≤1.

由 y=x2+ 1 4 ，y=k（x-a）+a2+ 1 4 ， 消去y整理得x2-kx+ka-a2=0.

由一元二次方程的根与系数的关系，得xA+xB=k，所以B（k-a，（k-a）2+ 1 4 ），

所以 AB = （k-2a）2+ （k-a）2+ 1 4 -a2- 1 4  2 = 1+k2 |k-2a|.

同理得 AD = 1+ 1 k2  · - 1 k -2a = 1+ 1 k2  ·  1 k +2a .

所以 AB + AD = 1+k2  k-2a + 1+ 1 k2  ·  1 k +2a ≥ 1+k2   k-2a +  1 k +2a  ≥ 1+k2  （k-2a）+  1 k +2a  = 1+k2  k+ 1 k  =  （1+k2）3 k2  .

令φ（t）= （1+t）3 t =t2+3t+ 1 t +3，其中k2=t，t∈（0，1），则φ′（t）=2t+3- 1 t2 = （2t-1）（t+1）2 t2 .

当00，

所以φ（t）在 0， 1 2  上单调递减，在  1 2 ，1 上单调递增，

从而当t= 1 2 时，φ（t）在（0，1）上取得最小值为φ  1 2  = 27 4 ，所以 AB + AD ≥ φ（t） ≥ φ  1 2   =  27 4  = 3 3  2 .

由于两处取得等号的条件不一致，于是2（ AB + AD ）>3 3 .

故矩形ABCD的周长大于3 3 .得证.

评析  试题考查了轨迹方程的求法，直线与曲线的位置关系，用导数研究函数单调性、最值等知识的应用，落实了高考“综合性”的考查要求.虽然试题是常见的命题形式，但其亮点比较突出：一是以往的圆锥曲线方程都是标准方程，而试题中的方程却是顶点不在原点的抛物线方程，它以二次函数的形式呈现；二是解析几何问题中渗透导数知识的运用，提升了试题的“综合”层次；三是在求解最值的过程中用到了“三角不等式[1]”这样一个“不怎么考”的知识点，这也启示我们只有把基础知识全面、扎实地掌握了，才能在考试中从容应对.

参考文献

［1］  鲁贤龙，朱小扣. 聚焦在解题中的三角不等式[J]．中学数学杂志，2022（11）：28-30．

作者简介  王兵（1981—），男，汉族，山东泰安人，中学数学高级教师;荣获泰山名班主任、泰安市优秀班主任、市直优秀教师、泰安市课程与教学工作模范班主任、泰安市课程与教学工作先进个人、泰山英才班主任、泰山教学新星、泰安市学科教学能力大赛二等奖、市直创新课一等奖、全国骨干班主任培训优秀学员等荣誉;主要从事高中数学教学及研究工作;表教学论文10余篇，主持市级课题1项，参与市级课题2项.