2.5D 机织复合材料悬臂梁振动疲劳实验与有限元模拟
邓杨芳 ,王雅娜
(1.中国航发四川燃气涡轮研究院,成都,610500;2.中国航发北京航空材料研究院 表面工程所,北京 100095;3.中国航发北京航空材料研究院 先进复合材料科技重点实验室,北京 100095)
三维机织复合材料是纺织结构复合材料的一个分支,是利用机织技术将纤维束织造成具有空间网状结构的预成型结构件,然后以预成型结构作为骨架进行浸胶固化而直接形成的复合材料结构。为了区别于三维编织复合材料,三维机织复合材料有时也被称为2.5D 机织复合材料[1]。由于独特的层间联锁结构,2.5D 机织复合材料比传统的层板复合材料具有显著的优势。从力学性能的角度,2.5D 机织复合材料具有更高的耐分层性、抗冲击性和损伤阻抗(切口不敏感性)。从设计的角度,2.5D 机织复合材料具有更优良的可设计性,可按实际需要设计纤维预制体,针对特定要求定制每个部位、不同方向的力学特性。从制造的角度,2.5D 机织复合材料对复杂形状的零、部件可实现整体织造,能够一次成型组合件,使加工量和连接大大减少。因此,2.5D 机织复合材料在航空、航天结构中得到越来越多的应用[2]。
未来大涵道比商用涡扇发动机的发展目标是高效率、低油耗、低排放,为了满足上述发展目标,采用复合材料风扇叶片是目前最为有效的技术途径。目前在发动机用复合材料叶片的选材有两种方案,一种是预浸料手工铺层/热压罐固化成型工艺,另一种是三维机织/传递模塑(RTM)成型工艺。20 世纪60 代末期,罗罗公司首次开展复合材料风扇叶片的研究。1985 年,GE 公司利用预浸料手工铺层+热压罐固化成型工艺,制造了GE90 商用涡扇发动机风扇叶片。然而铺层工艺制备的叶片由于层间性能薄弱,导致其抗外物冲击性能不足,2012 年,随着三维机织技术的出现,GE 公司采用三维机织结构+RTM 工艺制造了Leap-X 系列发动机复合材料风扇叶片,可获得更高的外形精度,并使叶片在鸟撞中保持足够的刚度和韧性。风扇叶片的安装采用根部固定在发动机风扇轮盘榫槽内的方式,当外激励的频率等于叶片的固有频率时叶片将发生共振导致疲劳断裂[3],因此振动疲劳是三维机织复合材料风扇叶片工程应用必须深入理解的一个问题。目前关于三维机织复合材料的振动疲劳行为的研究非常有限,有效的预测模型和分析手段也鲜有开发。
在实验研究方面,国内外学者广泛采用悬臂梁形式的试件,开展复合材料振动特性(固有频率、模态振型、阻尼特性)的测试,并分别研究了振动特性随纱线编织结构、疲劳循环次数等的变化规律[4-6]。杨强等[7]对复合材料可调叶片开展模拟发动机真实约束条件下的振动疲劳实验。在仿真模拟方面,目前2.5D 机织复合材料的有限元模型可以分为三大类,即细观有限元模型、宏观有限元模型和多尺度模型。细观有限元模型的方法主要用于材料细观力学分析,在考虑细观材料分布的精细化模型基础上,基于单胞尺度模型的应力场分析,预测材料的力学行为和损伤机理,研究者们在这方面已经开展了大量研究[8-10]。由于细观有限元模型涉及复杂的建模问题,且计算成本较高,很难应用于实际工程结构的力学性能分析,因此2.5D 机织复合材料结构以及复杂受力状态下的数值模拟大多采用宏观有限元模型[11]。近年来,兼顾计算精度和计算效率的多尺度模型逐渐发展成为2.5D 机织复合材料结构损伤模拟和强度预测的理想技术途径[12]。多尺度模型的基本原理是:在远离结构高应力水平的危险区域采用宏观模型模拟,在危险部位采用基于单胞的细观尺度模型进行预测[13]。多尺度模型目前已被广泛应用于机织复合材料结构加载下的应力分析和力学响应预测,但其在2.5D 机织复合材料振动疲劳行为模拟方面的应用还鲜有报道。
本工作利用实验与仿真相结合的手段探究2.5D机织复合材料悬臂梁振动疲劳行为,对2.5D 机织复合材料经、纬向试件分别开展设计应力水平下的振动疲劳实验,基于实验获得的材料振动疲劳损伤机制,建立2.5D 机织复合材料振动疲劳模拟的多尺度模型;基于主导的疲劳损伤机制建立纱线和基体的疲劳损伤萌生准则,结合复合材料疲劳加载模拟常采用的循环跳跃策略,采用固定周期跳跃法,分别针对纱线和基体选择恰当的剩余刚度模型,预测2.5D 机织复合材料经、纬向试件振动疲劳加载过程中工作段单胞内的应力场,并通过与试件断口形貌的对比验证模型的有效性。最后,利用建立的多尺度模型对2.5D 机织复合材料经向试件不同加载次数下内部损伤状态进行预测,揭示2.5D 机织复合材料振动疲劳损伤的演化机理。
1 2.5D 机织复合材料的振动疲劳实验
1.1 材料与试件
材料为一种发动机叶片用2.5D 机织复合材料,由中国航发北京航空材料研究院软材料研究中心提供,其中2.5D 机织预制体采用国产T800 制备,基体为一种热固性双马树脂EC230R。通过RTM 工艺制备获得的2.5D 机织复合材料板的名义厚度为4 mm,纤维体积含量为56%。2.5D 机织预制体由天津工业大学制备,图1(a)为2.5D 机织预制体编织结构示意图,编织参数详见参考文献[12]。2.5D 机织复合材料振动疲劳试件设计参考HB5722—1984 发动机叶片及材料振动疲劳试验标准,试件的构型和具体尺寸见图1(b),设计加工经、纬向振动疲劳试件各3 根,其中经向试件的长度方向沿着2.5D 机织复合材料的经纱方向,纬向试件的长度方向沿着2.5D 机织复合材料的纬纱方向。

图1 2.5D 机织复合材料振动疲劳试件(a)2.5D 机织预制体;(b)试件构型Fig.1 Vibration fatigue specimen of 2.5D woven composite(a)2.5D woven perform;(b)configuration of specimen
1.2 实验装置与实验方法
1.2.1 振动疲劳实验装置
振动疲劳实验装置包括一台1 吨推力电磁振动系统、一套专用实验夹具、一台Spider-81 型振动控制与动态信号分析系统、一台VIB2040 专用振动应变测量仪、一套ILD2310-40 型激光位移传感器、一个8324 型振动加速度传感器,上述仪器装置的信号将采用闭环控制方式进行采集和控制,通过控制输入-输出疲劳曲线相位角的一致性,实时追踪试件的共振频率,并控制振动台的激励频率始终等于试件的共振频率。
1.2.2 实验方法
(1)试件一阶弯曲模态频率测试
利用扫频测试方法获得2.5D 机织复合材料经、纬向试件的一阶弯曲模态的固有频率,即初始共振频率。
(2)应变-振幅关系标定实验
在试件工作段最小截面处的上表面粘贴应变片,将试件用特定夹具连接于振动台上,将振动台激振频率设定为试件一阶弯曲模态频率,开启振动台、动态应变采集仪以及激光传感器,通过调节加速度令试件获得不同的振幅,得到一组试件末端位移X、试件工作段中心上表面沿试件长度方向应变ε的数据,即为应变-振幅标定曲线。
(3)振动疲劳实验
对经向试件,选取2.5D 机织复合材料经向拉伸强度X1(数值为691 MPa)的0.32 倍作为其振动疲劳实验的最大设定应力水平,对纬向试件,选取材料纬向拉伸强度X2(数值为662 MPa)的0.29 倍作为其振动疲劳实验的最大设定应力水平。利用胡克定律计算经、纬向试件在设定最大应力水平下的应变值,根据应变-振幅标定曲线插值得到试件末端位移设定值。设定应力比R=-1,并设定激振频率等于试件初始共振频率,使试件末端位移逐渐增加到试件末端位移设定值后开始计数,停机判据为:材料破坏到一定程度导致共振无法保持。
1.3 实验结果
表1 为3 根经向试件和3 根纬向试件的振动疲劳实验结果,包括试件编号、末端位移、初始共振频率以及停机时的循环次数。采用光学显微镜对不同应力水下开展过振动疲劳实验的2.5D 机织复合材料经、纬向试件工作段侧面的断口形貌进行观察。采用微纳米焦点CT 扫描对疲劳实验后试件内部的损伤进行检测。
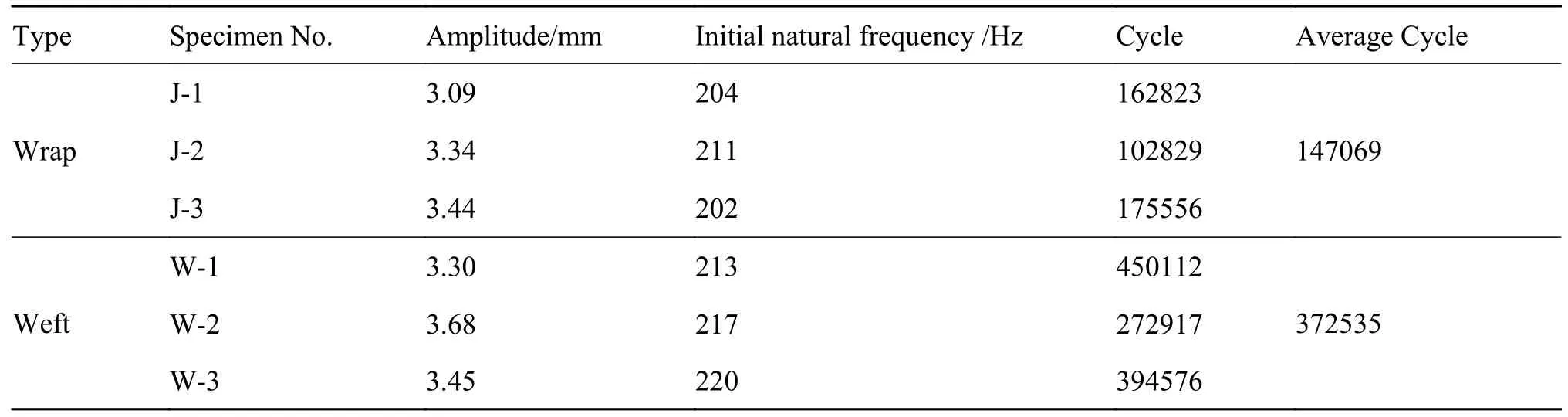
表1 经向、纬向试件的振动疲劳实验结果Table 1 Resonance fatigue test results of warp specimens and weft specimens
图2 为光学显微镜观察到的经、纬向试件经历振动疲劳实验后的工作段侧面的损伤状态。靠近试件上、下表面的区域可观察到纱线与基体之间发生了明显的界面脱粘。

图2 2.5D 机织复合材料试件断口形貌(a)经向;(b)纬向Fig.2 Fracture morphologies of 2.5D woven composite specimens(a)wrap direction;(b)weft direction
图3 为振动疲劳实验后经向、纬向试件工作段不同方向截面CT 图像。由图3 可见,经、纬向试件内部的损伤比侧面观察到的损伤更严重,材料内部不仅发生了明显的纱线与基体之间的界面脱粘,基体和纱线内部也都发生了不同程度的开裂,界面脱粘也主要是由于基体开裂所诱发的。
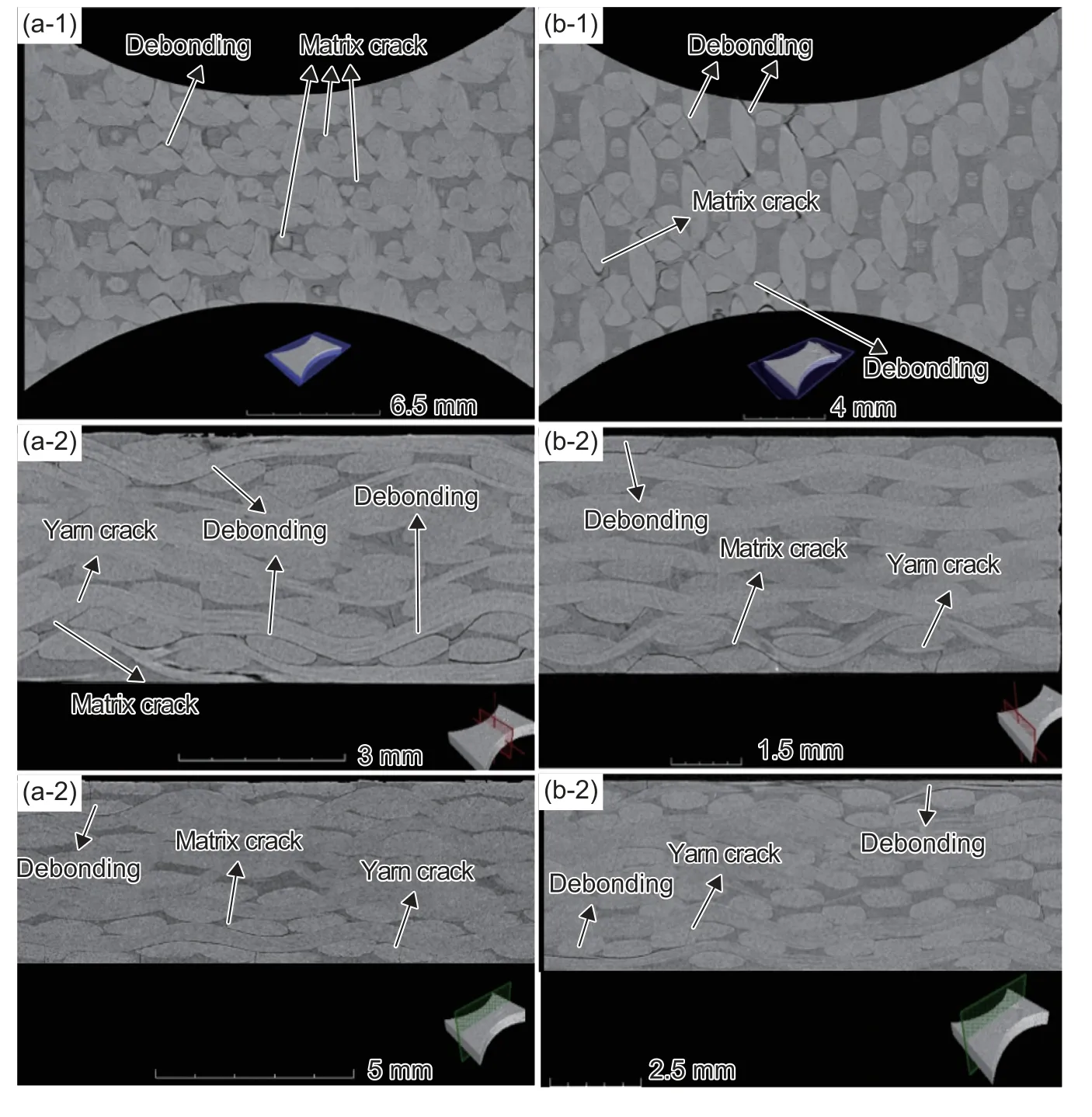
图3 2.5D 机织复合材料试件不同截面的CT 图像(a)经向;(b)纬向;(1)厚度方向;(2)长度方向;(3)宽度方向Fig.3 CT images of 2.5D woven composite specimens at different cross profiles (a)wrap-direction ;(b)weft-direction;(1)thickness direction;(2)length direction;(3)width direction
2 2.5D 机织复合材料振动疲劳仿真模型
2.1 2.5D 机织复合材料振动疲劳试件的多尺度模型
对试件大部分区域采用基于材料均匀化的宏观有限元模型,而对试件中部最窄截面区域(即工作段)采用考虑真实编织结构的全厚度单胞模型模拟,单胞模型以一定的方式“嵌入”宏观有限元模型中[14]。
(1)全厚度单胞模型
全厚度单胞模型的建模流程如图4 所示,采用英国诺丁汉大学设计开发的织物建模软件TexGen®建立2.5D 机织复合材料全厚度单胞的几何模型,尺寸为3.33 mm(经向)×5 mm(纬向)×4 mm(厚向)。单胞几何模型建模所需的纱线机织参数见表2。进一步设置基体、纤维组分的材料属性。纱线中T800 碳纤维是横观各向同性材料,其6 个工程常数包括纵向弹性模量Ef=295 GPa,横向模量Et=10 GPa,纵横剪切模量Gft=5 GPa,横向剪切模Gtt=5 GPa,纵横泊松比vft=0.3,横向泊松比vtt=0.4。基体采用EC230R,弹性模量为Em=4.5 GPa,泊松比vm=0.35。最后,基于单胞的几何模型生成可导入商用有限元软件ABAQUS®的单元网格,单元类型选为C3D8R,长、宽、高三个方向的单元数量均为80,并设置单胞模型的周期性边界条件[15-16]。

表2 2.5D 织物建模输入参数Table 2 Input parameters for 2.5D fabric modeling

图4 2.5D 机织复合材料全厚度单胞模型的建模流程Fig.4 Schematic diagram for full-thickness unit cell model of 2.5D braided composite
将TexGen®中导出的单胞模型inp 文件导入ABAQUS®中运行数值计算,进行单胞内部应力场的分析后运行TexGen®提供的脚本文件,得到2.5D 机织复合材料9 个工程常数的预测值。表3同时展示了2.5D 机织复合材料工程常数的预测值与测试值。实验仅能实测得到E1、E2、G12、ν12,利用单胞模型预测得到的上述四个工程常数与测试结果吻合较好,证明了基于单胞模型预测2.5D 机织复合材料宏观工程常数方法的适用性。
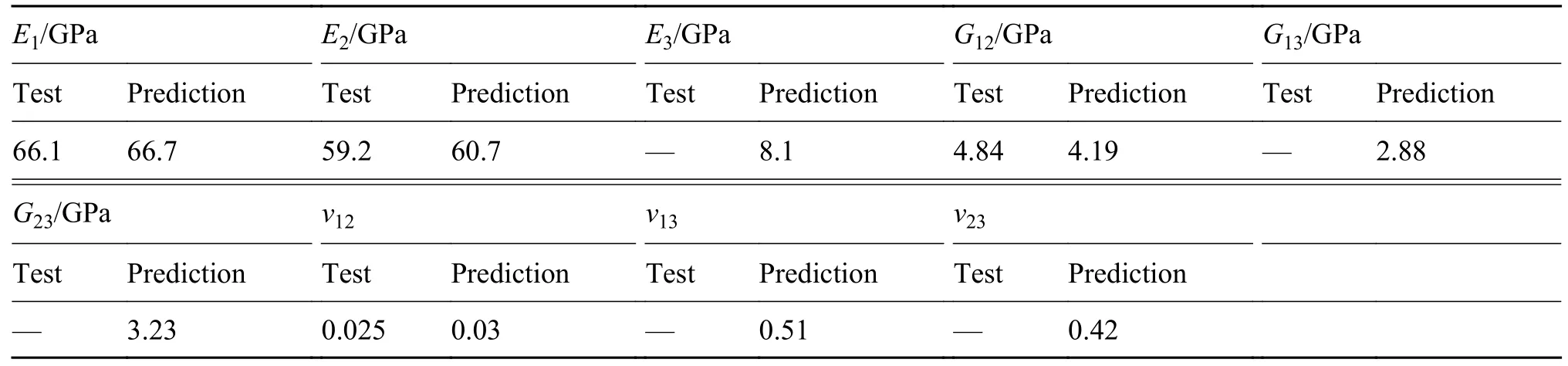
表3 2.5D 机织复合材料的工程常数Table 3 Engineering constants of 2.5D woven composite
(2)2.5D 机织复合材料振动疲劳试件的宏观有限元模型
图5 为2.5D 经、纬向振动疲劳试件的宏观有限元模型,模型采用减缩积分的8 节点六面体单元(C3D8R)。宏观模型建模时将材料等效为均匀的各向异性体,采用表3 中9 个材料宏观工程常数的预测值定义宏观有限元模型的材料本构。

图5 单胞模型四面网格嵌入宏观模型的示意图Fig.5 Schematic diagram of the four-sided mesh of an unit cell model embedded in a macro model
(3)基于宏观模型与单胞模型组装的多尺度模型
在ABAQUS®的装配模块导入2 个经向单胞模型和切除了中间部分的经向试件的宏观模型,利用merge 功能使2 个经向单胞模型共节点。然后,在ABAQUS®中建立经向试件的整体宏观模型,将宏观模型中间部分的最小截面处挖除一个3.32 mm×9.8 mm×4 mm 的区域。将由2 个经向单胞模型merge 得到的单胞模型嵌入经向试件宏观模型中间切除的部位,保证单胞模型前、后、左、右四个面各有一列完整的单元嵌入经向试件宏观有限元模型中,如图5 所示。利用ABAQUS®的嵌入式约束(embedded region),将单胞模型完全嵌入宏观模型中的节点约束到宏观模型中,得到经向试件振动疲劳模拟的多尺度模型,建模流程见图6。采用同样的方式,将3 个纬向单胞模型和切除了中间部分的纬向试件的宏观模型进行组装和集成,令单胞模型前、后、左、右四个面恰好各有一列完整单元被嵌入纬向试件宏观有限元模型。

图6 振动疲劳试件多尺度模型建模流程(a)经向试件;(b)纬向试件Fig.6 Multi-scale modeling process of vibration fatigue specimen(a)wrap direction;(b)weft direction
为确保不同尺度模型之间的边界协调,对宏观模型中嵌入单胞模型的区域采用与被嵌入的单胞模型完全相同的网格尺寸。宏观模型远离中部的区域采用较粗的网格,并使中部和两端区域的网格平缓过渡,以节省计算成本。根据实际工况施加边界条件:对2.5D 机织复合材料经、纬向试件宏观有限元模型左侧端面到距离变截面处0.5 mm 之间区域的上、下表面施加固支约束(U1=U2=U3=UR1=UR2=UR3=0);在宏观有限元模型的右端施加位移型载荷U3,令其等于试件末端振幅的平均值,如图7 所示。

图7 振动疲劳试件多尺度模型的约束与加载Fig.7 Restraint and loading of multi-scale model of vibration fatigue specimen
2.2 基于固定周期跳跃的疲劳加载模拟方法
拟采用基于固定周期跳跃的疲劳加载模拟策略,以每一次“加载-卸载后的再加载”的分析步模拟振动疲劳实验经历固定周次的循环[17]。每个周期跳跃的分析步采用疲劳损伤萌生准则和损伤后模量突降模型模拟损伤扩展,每个周期跳跃的分析步之间采用以循环加载次数控制的疲劳剩余强度模型模拟疲劳加载导致的材料性能退化,由此模拟振动疲劳实验中2.5D 机织复合材料试件工作段区域单胞内纱线、基体微观损伤的萌生和演变行为。本模拟中固定循环周次的跳跃值Njump为103,利用ABAQUS®软件的载荷步设置模块和载荷谱定义模块,通过特定的设置实现以分析增量步的逐步增加模拟循环加载次数以固定循环周次向前跳跃。具体设置如下:设置时间为1 的通用静态分析步,并设定为固定步长,步长值等于固定循环周次的跳跃值103除以疲劳寿命设定值(106)的0.5 倍(考虑加载和卸载),即0.0005。在载荷谱定义模块,采用“Tabular”类型定义“加载-卸载”循环模块,循环模块的个数等于疲劳寿命设定值(106)除以Njump,即为1000。
2.3 疲劳损伤模型和剩余强度退化模型
为了在基于固定周期跳跃的疲劳加载模拟方法下,实现2.5D 机织复合材料的疲劳加载过程中材料微观尺度(纱线、基体)的疲劳损伤演变预测,分别针对基体和纱线建立相应的疲劳损伤萌生准则和损伤后模量突降模型,以及由疲劳加载次数控制的疲劳剩余强度模型。其中,疲劳剩余强度模型用于定义由于疲劳循环加载次数累积导致的材料强度退化。考虑到疲劳加载主要导致基体和纤维束内微裂纹的产生和裂纹密度增加,疲劳剩余强度模型只考虑基体抗拉强度和纤维束内横向抗拉强度的衰减。
(1)基体疲劳损伤萌生准则与模量突降模型
基体组分的疲劳损伤萌生准则定义为:基体的Von Mises 应力大于基体抗拉强度σm[18];在本工作的模拟中,基体的抗拉强度σm为119 MPa。基体损伤后性能的退化通过如下模量突降法则定义:当基体的应力水平满足基体的疲劳损伤萌生准则时,将基体的弹性模量Em降为极小值(0.001 MPa)。
(2)纱线疲劳损伤萌生准则与模量突降模型
根据疲劳后断口形貌的观察,纱线的主导损伤模式为纤维束间的破坏,以及纱线与基体之间的脱粘,其中纱线与基体之间的脱粘又是由于为纤维束间的开裂所诱发的,因此纱线的疲劳损伤萌生准则定义为:纱线中横向应力(S22)或纱线厚度方向应力(S33)大于纱线横向抗拉强度,鉴于纱线在横向都是靠基体粘合在一起,因此认为纱线的横向抗拉强度Yt等于基体的抗拉强度σm。当纱线的应力水平满足纱线的疲劳损伤萌生准则时,将纱线的横向模量Et,纱线纵横剪切模量Gft,纱线横向剪切模量Gtt同时降为极小值(0.001 MPa)。
(3)基体的疲劳剩余强度模型
基体组分的疲劳剩余强度模型参考Palmgren-Miner 理论,定义为:
式中:Rm为基体的剩余强度值;k表示第k次固定周期跳跃;j表示模拟的固定周期跳跃数;σm为基体准静态抗拉强度值;Njump表示固定循环周次(本工作Njump=103);表示当下应力水平下的最大疲劳周次,根据基体的疲劳S-N曲线插值确定。
(4)纱线的疲劳剩余强度模型
纤维组分的疲劳剩余强度模型同样参考Palmgren-Miner 理论,定义为:
式中:RT为纤维的剩余强度值;Yt为纱线横向拉伸强度值。
为了将上述疲劳损伤模型和剩余强度退化模型嵌入多尺度有限元模型的数值计算中,将根据上述定义的疲劳损伤萌生准则和模量突降模型的数学表达,以及疲劳剩余强度模型的数字表达式编写umat 子程序,并在umat 子程序中根据疲劳损伤萌生准则的数学表达式定义纱线和基体的损伤状态变量(statev),以便在数值计算结果中指示纱线和基体的损伤程度。
2.4 有限元模型有效性验证
图8(a)为模拟经历了147000(接近经向试件的疲劳寿命平均值147069)次循环后,2.5D 机织复合材料经向试件全厚度单胞内6 个应力分量的应力云图。S11 最大值出现在单胞模型长度方向的中间截面处,从试件厚度方向看,S11 最大值位于试件弯曲加载的受拉一侧。S11 最大值为3047 MPa,远低于纤维抗拉强度(6017 MPa),因此纱线中的纤维不会发生断裂。纬纱承受较大的横向应力,试件宽度方向一侧纬纱中的S22 最大值达到180 MPa,鉴于纱线的横向承载能力由基体强度决定,这个值已经超过了基体抗拉强度(119 MPa),因此纬纱在振动疲劳实验中将发生横向开裂。S33 的最大值出现在单胞靠近夹持端的截面处,位于靠近试件表面的经纱中,最大值高达304 MPa,已经远远超过基体抗拉强度,因此经纱在振动疲劳实验中会发生劈裂。整个单胞内部S12 的水平普遍不高,仅在单胞前、后截面处有比较大的值。整个单胞内部S13 的水平普遍较高,尤其在经纱、衬经纱与基体的交界处S13 非常显著,最大值高达150 MPa,远高于材料经向层间剪切强度(57.1 MPa),因此振动疲劳实验中试件内的经纱、衬经纱与基体会发生脱粘。整个单胞内部S23 的水平较低,最大值为42 MPa,出现在经纱、衬经纱与基体之间的交界处,由于这个值低于材料经向层间剪切强度,因此不会发生引起纱线与基体之间的脱粘。图8(a-7)展示了单胞模型内基体的Mises 应力云图,根据2.5D 机织复合材料的基体开裂准则[18],当基体中的Mises 应力超过基体强度时,基体将发生开裂,以基体抗拉强度值为门槛值,令云图中Mises 应力超过该门槛值处显示为灰色,可见基体中许多区域的应力水平达到了基体开裂强度,并且Mises 应力最大值高达322 MPa,超过了基体抗拉强度,因此试件在振动疲劳过程中,内部必然会发生严重的基体开裂。综上可知经向试件的振动疲劳实验过程中,将会发生的损伤有纬纱开裂、经纱劈裂、基体开裂以及经纱、衬经纱与基体脱粘,上述预测结果与内部损伤的CT 图像基本一致。

图8 试件单胞内应力云图(a)经向;(b)纬向;(1)S11;(2)S22;(3)S33;(4)S12;(5)S13;(6)S23;(7)Mises stressFig.8 Stresses maps of unit cell in specimen(a)wrap direction;(b)weft direction;(1)S11;(2)S22;(3)S33;(4)S12;(5)S13;(6)S23;(7)Mises stress
图8(b)为利用多尺度模型模拟经历了373000(接近纬向试件的疲劳寿命平均值372535)次循环后的2.5D 机织复合材料纬向试件全厚度单胞内6 个应力分量的应力云图。在振动疲劳实验过程中试件宽度方向靠近两侧的单胞中的纱线承受大部分弯曲应力,并且两侧的单胞中靠近试件下表面受拉一侧的纬向纱线承受最大的纤维抗拉应力,S11 最大为2762 MPa,远低于纤维抗拉强度,因此振动疲劳实验过程中纱线中的纤维不会断裂。S22 显著部位位于工作段中间单胞内的纬向纱线中,最大值高达240 MPa,超过了基体抗拉强度,因此振动疲劳实验过程中试件中部的纬纱将发生横向开裂。S33 最显著部位出现在最中间一个单胞内的经向纱线中,所在截面距离单胞靠近夹持端的截面约1 mm 处,S33 最大值为121 MPa,超过了基体抗拉强度,因此纬向试件的振动疲劳实验过程中试件中部的经纱也会发生劈裂。经纱和衬经纱与基体之间界面处的剪切应力S12 较高,可能导致纱线与基体之间的脱粘。S13 最显著部位位于单胞靠近夹持端的截面处,出现在纬纱与基体界面之间,最大值高达137 MPa,超过了材料纬向的层间剪切强度(64.8 MPa),也会导致纱线与基体之间的脱粘。单胞内S23 的应力水平整体较低,不会引起纬纱与基体界面脱粘。图8(b-7)展示了单胞模型内基体中的Mises 应力的云图,云图显示设置时同样令Mises 应力超过基体强度的部分显示为灰色。可见纬向试件的单胞内,有许多部位的基体Mises 应力超过基体抗拉强度,最大值高达266 MPa,因此纬向试件工作段最小截面部分的基体中也将发生严重开裂。综上可知纬向试件的振动疲劳实验过程中,将会发生的损伤有纬纱横向劈裂、经纱劈裂,纬纱与基体脱粘,基体开裂等,预测结果也与断口观测结果吻合。
2.5 振动疲劳加载历程中损伤演化过程模拟
根据单胞应力场的分析结果以及内部损伤形貌的观察结果,基体的开裂引发纱线与基体脱粘,是导致2.5D 机织复合材料疲劳破坏的主要因素,因此在umat 子程序中根据基体开裂准则定义指示基体损伤的损伤状态变量(statev),可以从计算结果中逐增量步地查看单胞模型中损伤状态变量(statev)的云图,在软件界面下损伤状态变量(statev)显示为符号SDV。设置当SDV 大于1 时云图显示为黑色,SDV 的数值则指示了损伤程度。分析增量步每增加一步,代表模拟的振动疲劳循环加载次数向前跳跃了固定循环周次N0=103,通过逐分析增量步地查看单胞内SDV 的云图,可得到疲劳循环加载次数每累计103次后,振动疲劳试件工作段单胞内损伤状态的演变规律;图9 为2.5D 机织复合材料经向试件分别经历了50000、100000、140000 次循环后,工作段材料内部微观损伤状态的模拟结果。可见,随着循环次数的增加,单胞内部的损伤区域逐渐变大,单胞内部的基体损伤程度也越来越严重,基体损伤诱发纱线与基体之间的界面脱粘,造成纤维“骨架”与基体全面分离,导致材料内部载荷难以传递,悬臂梁试样发生彻底失效。

图9 经向试件不同循环次数下的损伤状态模拟结果(a)50000 次;(b)100000 次;(c)140000 次Fig.9 Simulated results of damage state of wrap-direction specimens under different cycles(a)50000 cycles;(b)100000 cycles;(c)140000 cycles
3 结论
(1)2.5D 机织复合材料经、纬向试件在振动疲劳实验过程中内部的微观疲劳损伤模式类似,包括纱线与基体之间的脱粘、基体开裂、纱线内纤维束间的横向劈裂等。
(2)建立的2.5D 机织复合材料振动疲劳试件的多尺度模型,以及开发的基于固定循环周次跳跃策略渐进疲劳损伤模型可准确模拟试件工作段单胞内的应力场,以及单胞内纱线和基体疲劳损伤的演变,与观测到的试件断口形貌特征基本吻合,验证了本工作数值预测模型的有效性。
(3)基体开裂对2.5D 机织复合材料的振动疲劳损伤具有关键影响,2.5D 机织复合材料振动疲劳损伤的机制为:基体开裂诱发纱线内部纤维束间的横向开裂,进一步诱发纱线与基体之间脱粘,造成纤维“骨架”与基体脱离,复合材料纤维、基体协同承力的一体化结构被破坏,材料内部载荷无法有效传递,导致试件的最终失效。

