面向高速切削的钛合金Ti-6Al-4V动态本构模型：综述

姜紫薇 ,杨 东* ,陈建彬

（1.安徽大学 机械工程系，合肥 230601；2.安徽天航机电有限公司，安徽 芜湖 241000）

钛合金Ti-6Al-4V（TC4）材料因其优良的力学性能和机械性能，如高强度、高硬度，良好的热稳定性和耐腐蚀性等，被广泛地应用于国防工业等领域[1-3]。TC4 钛合金属于典型的难加工材料，在加工时存在变形系数小、切削温度高、弹性回复大、易于生成加工硬化层等问题[4-5]。高速切削加工作为一门先进制造技术已得到广泛应用，实践表明高速切削不仅能够提高钛合金等难加工材料的去除效率，还可以改善其加工表面质量[6]。钛合金高速切削加工过程具有高温、高应变和高应变率的热力强耦合非线性动态特征，为了有效调控钛合金切削性能，需要对钛合金高速切削过程动态力学行为进行准确表征和评价。

动态本构模型可以描述材料在大变形、高应变率、高温等载荷作用下复杂动态力学行为，对研究金属材料在强载荷作用下的热力学响应有着重要的意义，是研究切削加工变形的理论基础[7]。本文以TC4 钛合金为研究对象，从TC4 钛合金高速切削过程的动力学特点出发，分析了切削变形区的温度响应和应变率响应的变化规律，提出了探究动态本构模型的必要性。同时，对比了Johnson-Cook（J-C）模型、Zerilli-Armstrong（Z-A）模型及其修正模型和Bammann 模型在构建时的理论依据、适用条件、优缺点及预测精度，发现预测值与实验值存在一定误差。经综合比较，选取J-C 模型进行探究。可将J-C 模型修正的方法归为两类：基于温度影响的修正及基于竞争机制影响的修正，对比修正后的预测精度与经典模型的预测精度。最后根据不同构建方法的理论依据及优缺点，给出高速切削钛合金Ti-6Al-4V 本构模型的表征所面临的关键问题和主要发展方向。

1 TC4 钛合金高速切削过程动力学特点

高速切削载荷作用下，工件材料的动态力学特点主要体现在高应变率和高温等方面。TC4 钛合金在不同的切削工艺条件下应变率、温度敏感性不同，且应变率、温度变化范围大。

1.1 切削变形区应变率响应

TC4 钛合金在高速切削过程中会产生高应变率，相同温度条件下，流动应力随着应变率的增加而增大，表现出应变率强化效应[8]。高速切削过程中的塑性变形是加工硬化与软化的综合过程。TC4 钛合金在高应变率下的软化需要足够的时间来完成，否则在切削过程中的硬化率大于软化率，会生成加工硬化，导致应力升高。

刘战强等[9]计算了高速切削条件下TC4 钛合金应变率随切削速率的变化趋势。在切削速率为0～400 m/min 范围内，应变率理论值呈现上升趋势，且增幅逐渐增大。在0～300 m/min 时应变率增大280000 s−1，在300～400 m/min 时应变率增大220000 s−1。朱水生[10]利用AdvantEdge 软 件 对TC4 钛合金进行了100～500 m/min 的切削仿真，发现最大应变率的集中区域在切屑和剪切带之间不断转化。在100 m/min 的切削速率下没有出现明显的集中变形的行为，应变率小于8000 s−1；当切削速率升高至300、500 m/min 时，剪切带中则有明显的集中变形行为，应变率达到105s−1，切屑开始呈现锯齿形态。王情情等[11]开展了切削速率在180～3000 m/min 范围内的TC4 钛合金直角切削实验，研究结果表明，切削速率在180～2500 m/min范围内，切屑绝热剪切带内的应变率由105s−1增大到107s−1，切屑锯齿化程度加剧，发生严重塑性变形。切削速率高于2500 m/min 时，材料发生韧性断裂，绝热剪切带破坏，应变率无明显变化。为探究高速切削时切削速率对应变率的影响，计算了400～800 m/min 范围内的锯齿化程度，发现在400～600 m/min 之间锯齿化程度大幅上升，在600～800 m/min 之间锯齿化程度几乎不变。

综合上述文献，当切削速率低于300 m/min时，产生带状切削。切削速率高于300 m/min 时，剪切面的温度升高，导致了TC4 钛合金的热软化效应大于应变硬化效应和应变率硬化效应，使得材料发生塑性流动。同时第一变形区的承载能力下降，发生热塑性失稳，开始产生锯齿形切屑。在切削速率小于900 m/min 范围内，应变率随切削速率的增大而增大，且增幅也逐渐增大，如图1 所示。

图1 应变率随切削速率的变化趋势Fig.1 Variation trend of strain rate with cutting speed

1.2 切削变形区温度响应

TC4 钛合金具有化学活性高、导热性能差等特点。高速切削使工件处于高温加工环境，在发生塑性变形时，除了原子跃迁加快会引起塑性流动加剧，还可能发生动态回复和再结晶两种软化机制[12]。若工件表层温度升高过大，会造成表面的完整性下降。在高速切削过程中，切削层的剪切区会因为剪切变形，前刀面与切屑产生摩擦，后刀面与已加工表面摩擦而产生切屑。同时，切削速率的提高也加快了切屑的流动速率，切屑上的热量随着高速流动的切屑被带走，减少了传递到刀具和工件表面上的热量[13]。

胡敏敏[14]探究了TC4 钛合金在切削速率为90～135 m/min 范围内铣削结果，利用AdvantEdge FEM 软件进行了顺铣和逆铣的仿真，结果表明两种情况下切削速率从90 m/min 升高至135 m/min，切削温度从725 ℃上升至830 ℃。杨振朝等[15]采用AdvantEdge FEM 软件对TC4 钛合金进行了113～377 m/min 范围内的二维模拟仿真，发现切削区的最高温度发生在刀-屑接触面上，距离刀尖0.01～0.02 mm。随着铣削速率的增加，刀尖处切削区温度经历上升-下降-上升，温度总增幅约为700 ℃，切削区的最高温度为1116 ℃。许光彬等[12]利用Deform-3D 模拟了切削速率为60、100、140、180、220 m/min 的TC4 高速切削，发现切削速率在60～100 m/min时，切削温度由440 ℃增加到650 ℃；高于100 m/min时，切削温度增加约80 ℃，增幅较慢，最后达到相对波动幅度较小的稳态范围内。胡木林[16]建立了TC4 钛合金的Deform-3D模型，进行了切削速率为60～240 m/min 的高速切削仿真，得到的仿真结果与文献[12]具有高度的一致性。图2 为切削温度随切削速率的变化趋势。

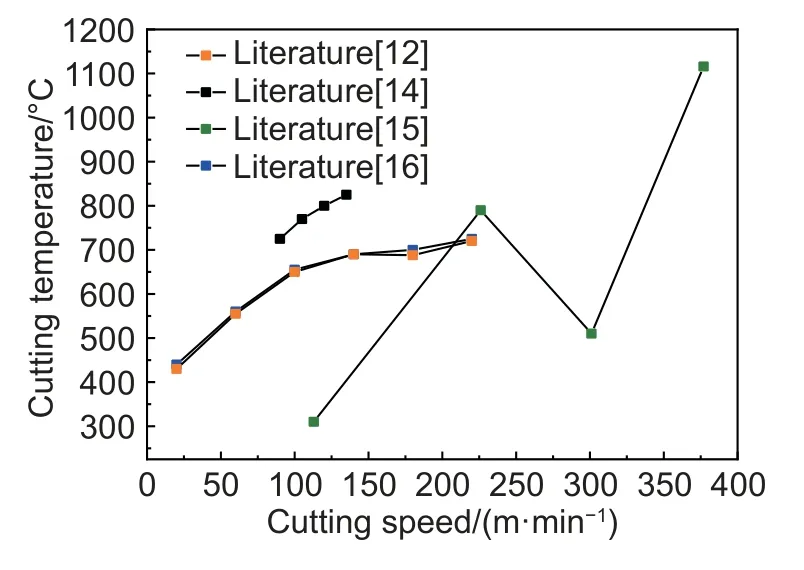
图2 切削温度随切削速率的变化趋势Fig.2 Variation trend of cutting temperature with cutting speed

TC4 钛合金相变温度在980～990 ℃范围内，在高速切削过程中，由于切削会带走大量热量，所以切削速率低于300 m/min 时不会发生相变。当切削速率低于250 m/min 时，切削区温度随切削速率的增大呈现上升的趋势，且增幅逐渐减小。这是由于切削速率较低时，刀具与切屑之间产生较大的摩擦力和切屑剪切滑移力，切削力做功导致单位时间内产生的切削热增多，故切削温度升高快。随着切削速率的升高，切削流动加快，带走的热量增多，但温度总体仍呈现上升的趋势，出现升高幅度减慢的情况。

用于描述TC4 钛合金高速切削过程力学响应的本构模型主要分为两类，一类是唯象本构模型，如Johnson-Cook 模型；另一类是物理学本构模型，如Zerilli-Armstrong 模型、Bammann 模型等。唯象本构模型主要根据实验过程中的现象，总结其在不同应变、应变率、温度等条件下应力-应变关系的响应规律[17]，从而得出相应的关系式。而物理学模型主要是从材料的内部结构如晶粒尺寸、位错密度等出发，认为变形条件取决于材料的内在结构[18]。

2 TC4 动态本构模型

2.1 Johnson-Cook 模型

Johnson-Cook 模型综合考虑了材料的应变硬化、应变率硬化和热软化效应，描述了材料在不同应变、应变率、温度和压力下的应力-应变对应关系[19]。由于其参数少，各项因子具有明确的物理意义，目前被广泛使用，如式（1）所示：

式中：A、B、C、m、n为待定参数；σ为Von Mises 流动应力；ε为应变；为应变率；为参考应变率；Tr为参考热力学温度；Tm为材料的熔点；T为实验温度。第一项表示应变硬化效应，第二项表示应变率硬化效应，第三项表示热软化效应[2]。

崔奎虎[20]开展了应变率范围为0.01～4000 s−1，温度范围为20～900 ℃的分离式Hopkinson 压杆（SHPB）实验，绘制了应力-应变曲线图，并且拟合了J-C 模型。图像表明从常温到300 ℃条件下，材料看不到明显的屈服点；从500 ℃升高到900 ℃，材料表现出典型的弹塑性特征，应变硬化现象不明显。且材料的屈服强度随着温度的升高降低，500 ℃屈服应力是900 ℃的两倍。将相同温度条件下本构模型的预测曲线与实验曲线进行对比，应变率为2500 s−1时最大误差不超过9%；应变率为4000 s−1时，最大误差不超过5%。惠旭龙等[21]利用SHPB 装置探究了应变率为500、1500 s−1和2500 s−1时TC4 钛合金的动态力学性能。当塑性应变为0.02、0.04 和0.07 时，与准静态条件相比，三种不同应变率下的流动应力分别增大27.8%、25.1%和22.4%，应变率硬化效应减弱。同一应变率下，随着应变的增加，流动应力分别增大1.6%、1.5%和1.3%，应变硬化效应也减弱。利用实验得到的数据进行J-C 本构模型拟合，该模型最终的仿真结果与实验结果之间误差均在5%以内。朱文明[22]开展了应变率范围为10−3～104s−1的动态实验，并探究了动态条件下应变率和温度对流动应力的影响，拟合了J-C 模型的参数。利用ABAQUS软件进行切削速率为107、166、210 m/min 的TC4 钛合金高速切削仿真，得到的仿真主切削力与实验值误差在10%左右，并且不同温度下仿真得到的最高温度比实验测得平均温度约高260 ℃。

上述学者所得到的J-C 模型参数如表1 所示，对比模型参数发现应变率敏感系数的大小与参考应变率呈负相关[21]。在常温状态下，随着应变率和应变的增加，应变硬化和应变率硬化效应都在减弱，说明存在相互耦合的现象。在高温状态下，由于TC4 钛合金的强度降低，应变率对材料的影响很小，使得相同温度下准静态与高应变率的应力应变曲线基本重合。对比高速切削时的仿真结果与实验结果，误差均不大于10%。

表1 文献中获得的TC4 钛合金的J-C 模型参数Table 1 J-C model parameters of TC4 titanium alloy obtained in literature

2.2 Zerilli-Armstrong 模型

在较高的应变率下，特别是在冲击载荷作用下，位错运动速率的提升来不及协调多余的塑性变形，此时需要位错生成机制参与塑性变形。Zerilli 等[23]研究发现不同组织结构的金属具有不同的热激活机理，基于微观位错机理的角度提出了用于体心立方（BCC）和面心立方（FCC）金属的Zerilli-Armstrong 模型。TC4 钛合金由密排六方（HCP）结构的α 相和体心立方（BCC）结构的β 相组成，在室温至980 ℃时，TC4 钛合金为α+β 相组织；在980～1030 ℃范围内TC4 钛合金为β 单相组织，软化机制主要为动态回复，且该温度范围内流动应力对温度敏感程度较低，高应变率变形产生热效应对流动应力的影响不大[24-25]。因此，在进行TC4 钛合金高速切削时大多采用BCC 型本构模型，如式（2）所示：

式中：C1～C5和应变硬化指数n为Z-A 模型的材料参数；σ为Von-Mises 流动应力；为参考应变率。Z-A 模型的假设条件会影响其精度，在BCC 晶格结构的材料中，假设其应变硬化指数与温度、应变率无关。该模型兼顾了材料的应变强化效应、应变率硬化效应和高温热软化效应[26]，适用于TC4 钛合金高速切削时应变率≤104s−1的条件下。但忽略了应变率和温度对材料加工硬化的影响。大应变的加载条件下，应变率、温度和应变的耦合作用显著，所以不能准确反映材料的动态力学性能[27]。Macdougall 等[28]开展了TC4 钛合金在100 ℃、应变率为300～1000 s−1范围内的拉伸实验，结合红外线放射仪测量实验过程中产生的绝热温升，确定了Z-A 模型的参数。利用ABAQUS 软件进行仿真预测，发现 Z-A 模型在应变率为3500 s−1以内拟合误差20%，在3500 s−1以上则无法准确描述材料的加工硬化效应。

Liu 等[29]考虑了切削加工中TC4 钛合金绝热剪切带形成过程中孔洞和微裂纹等破坏机制对材料流动强度的影响，将捕捉合金在高应变和高应变率下承载能力损失的失效函数与Z-A 模型相结合，扩展了HCP 金属的Z-A 模型，用于相变温度以下的实验条件。该模型描述Ti-6Al-4V 合金在大应变范围和应变率下的流动强度，其预测的切屑锯齿化程度与实验值的平均误差在25%以下。如式（3）所示：

式中：σa由溶质原子和晶界引起的流动应力的非热分量；β0、β1、B0、α0、α1是材料常数；εr是动态恢复的特征应变；失效函数由括号中的第二项给出，由三个应变率相关参数H、a和k控制。为了补充温度在动态力学性能过程中的影响，LS-DYNA 软件中对Z-A 模型进行了修正。在Z-A 修正模型[30]增加了一项温度多项式函数来反映温度对预测的影响，如式（4）、（5）所示：

式中：μT为温度T时的剪切模量；μ293为293 K（室温）时的剪切模量。

Z-A 模型的构建基于金属材料的晶格种类，TC4 钛合金在达到再结晶温度时会发生相变，由α+β 相组织转变为β 单相组织。因此，Z-A 模型可以描述未发生相变的温度和应变率的实验范围，无法同时准确描述相变温度前后的动态力学性能。

2.3 Bammann 模型

Bammann[31]认为材料力学特性是与温度相关的，需从热力学角度进行考察。将力学与热力学对材料的共同影响作为建立本构模型的依据，基于此提出的黏塑性耦合本构模型—Bammann 模型。该模型可以捕捉材料的变形过程，且适用于大应变、高应变率和蠕变等变形情况[32-33]。Bammann模型的黏塑性流动法则如式（6）所示，硬化内变量演化方程如式（7）、（8）所示：

式中：C1～C18为材料参数；V（T）表示屈服应力的速率相关性大小；Y（T）表示与速率无关的屈服应力；f（T）表示速率相关性对初始屈服应力的影响；rs（T）和Rs（T）是描述扩散控制的静态或热恢复的标量函数；rd（T）和Rd（T）描述动态恢复的标量函数；h（T）表示各向异性硬化模量；H（T）为各向同性硬化模量。

Guo 等[34]开展了温度为20、500、700、900、1100 ℃，应变率为800、1700、2000、2500 s−1的SHPB实验，采用非线性最小二乘法拟合Bammann 模型。将预测值与实验值的应力-应变曲线进行比较，发现Bammann 模型塑性阶段的预测误差约在10%以内。当应变率高于1700 s−1时，模型的预测误差约在5%以内。张雪强[35]开展了温度为200～400 ℃，应变率为0.001～5000 s−1范围内的SHPB实验，经平滑处理后的实验曲线与计算曲线在塑性阶段的后50%应变内吻合度高。在屈服点附近实验曲线高于预测曲线，最大误差约为150 MPa。

Bammann 模型适合预测大应变阶段的应力值，利用Bammann 模型所测的应力—应变曲线塑性阶段内，预测精度随着应变率的提高而提高。由于SHPB 实验时基于均匀化假设的，而实际实验中试件中的应力波一般需要在试件中传播三个来回才能达到均匀。因此，在实验初始阶段应力还未均匀化，导致预测值与实验值在应变前期的误差大于后期。

2.4 模型拟合结果对比

不同的本构模型旨在准确描述TC4 钛合金切削时的动态力学行为。已有学者对不同本构模型的预测能力进行了对比。胡绪腾等[33,36]开展了200～400 ℃、应变率为103～106s−1的SHPB 实验，分别拟合了J-C 模型、Z-A 修正模型[30]和Bammann模型，发现三者在200～400 ℃、应变率为1000～5000 s−1时预测值与实验值具有较好的一致性。利用最小二乘法对模型参数进行优化，优化目标为模型预测结果与实验结果的误差平方和最小。单从模型计算曲线与实验曲线之间的累积误差看，Bammann 模型材料参数优化的目标函数值为21995，为三者中的最小值；Z-A 修正模型误差函数值为28465；J-C 模型的为30775。陈敏[37]开展了20～400 ℃、500～5000 s−1应变率的SHPB 实验，并拟合了J-C 模型和Z-A 修正模型。利用ANSYS/LS-DYNA 软件仿真了200 ℃、3000 s−1应变率的实验。将仿真结果与实验数据进行对比，发现相同应变率时，室温条件下J-C 模型的预测精度最高，这是由于J-C 模型的拟合参考条件为室温下准静态。由表2 可以看出，该拟合范围内J-C 模型的拟合误差小于Z-A 模型。

表2 J-C 模型与Z-A 修正模型拟合误差Table 2 J-C model and Z-A model fitting error correction

张一雨等[38]开展了TC4 钛合金在850～1050 ℃、不同应变率下的等温热压缩实验，利用实验数据进行了J-C 模型、J-C 修正模型[26]和Z-A 修正模型[26]的拟合。三种本构模型的预测应力值与实验应力值的对比结果如表3 所示，可以看出J-C 修正模型的预测精度高于其余两种模型。

表3 各模型拟合结果对比[38]Table 3 Comparison of fitting results of each model were compared[38]

刘东等[39]利用有限元分析软件Deform 对TC4 钛合金进行正交切削仿真，分别使用J-C 模型、Z-A 模型、Deform 软件自带本构模型（σ=σ（ε，˙ε，T））进行建模。将仿真得到的x、y向的切削力与实验结果进行对比，结果表明Z-A 模型仿真结果的x、y向切削力仿真值最大，偏离实际切削力值最多；Deform 自带本构模型和J-C 模型的仿真结果与实际切削力值最为接近，且随切削速率的增大，仿真切削力结果周期性变化更明显。

J-C 模型是利用准静态条件下的实验参数进行拟合的，在室温条件下的预测精度高与Z-A 模型。但在实验温度高于850 ℃时，预测结果相反。这是由于Z-A 模型基于微观位错机理，对于不同的晶格建立不同的本构模型。TC4 钛合金在850～1000 ℃会由于再结晶发生相变，即准静态条件下相变后的Z-A 模型的拟合精度高于J-C 模型。应变率在500～10000 s−1条件下，J-C 模型总体的拟合精度高于Z-A 模型，且随着温度的升高，拟合误差整体呈现增大的趋势。与Bammann 模型相比，J-C 模型在塑性阶段前期拟合精度高，而Bammann 模型在塑性阶段后期拟合精度高。各本构模型的优缺点如表4 所示。综合多组条件来看，在描述TC4 钛合金高速切削动态力学性能时，选取J-C 本构模型最佳。

表4 本构模型在TC4 钛合金高速切削仿真中的优缺点Table 4 Advantages and disadvantages of constitutive model in high speed cutting simulation of TC4 titanium alloy

3 J-C 本构修正模型

J-C 模型因具有形式简单、参数数量少的优点，在金属动态力学性能的描述中得到广泛应用。但是，经典J-C 模型将力学行为归结为三种效应相乘，彼此相互独立且不存在耦合关系。在描述TC4钛合金高速切削时高应变率和高温条件下的描述能力较差，与材料的实际流变行为不一致，降低了表征精度[40]。鉴于此，国内外学者开展了基于经典J-C 模型的修正本构模型研究，主要包括应变-应变率-温度耦合效应修正和温度影响修正等。

3.1 基于温度影响修正

高应变率下材料快速变形产生的热能，一部分耗散到自然界中，另一部分使材料自身温度升高。由于加载速率快，TC4 钛合金表现出热黏塑性，即内部温升来不及扩散，导致应变、应变率的强化作用减弱，从而出现流变应力在高温下软化的现象。经典J-C 模型假设热软化行为是线性的，然而热软化会出现高温饱和现象，从而使流动应力不随温度的升高而线性减小[41]。

王琪等[42]发现当材料的温度高于再结晶温度时，可能会发生动态再结晶以及相变现象，导致阻止局部变形的应力减小，发生软化现象。因此引入连续温度函数式Y（T），提出了一种考虑动态再结晶软化的修正模型，如式（18）、（19）所示：

式中：r和s为再结晶软化指数；Tc为再结晶温度。分别提取应变率1400 s−1时，800 ℃和1000 ℃下预测应力值进行比较，修正后的预测值与实验值误差在4%以内。

刘丽娟等[7,43]开展了815～955 ℃及1000～1100 ℃范围内的等温恒应变率压缩实验的动力学研究，发现TC4 钛合金变形热激活能远大于其自扩散激活能，发生热软化现象，流动应力值下降显著。通过添加一项影响因子H（t）来反映高温发生相变时的应力-应变的曲线变化趋势，如式（20）、（21）所示：

式中：（σf）bc为再结晶之前的流动应力；（σf）ac为再结晶之后的流动应力；Tc为再结晶温度；f（T/Tc）是一个关于温度的取整函数。利用AdvantEdge FEM 有限元软件对经典J-C 模型和修正J-C 模型进行有限元仿真，结果表明在相同的切削条件下，当温度超过850 ℃时，修正J-C 模型的流动应力急剧下降，下降幅度为46.7%；而经典J-C 模型的流动应力下降平缓，下降了11%。

随着塑性应变的增大，TC4 钛合金在高应变率下流变应力的变化梯度比准静态下流变应力的变化梯度更平缓，甚至出现动态应力-应变曲线和准静态应力-应变曲线相交的现象[44]。曾祥国等[45]基于功热转换原理，通过引入功热转换系数h，对J-C 模型温度项进行修正。h与应变率呈正相关，当→∞时，h→1（h=1 为绝热状态），如式（22）所示：

式中：ka、kb、kc为应变率敏感材料常数，需要通过实验数据来确定，且有-1＜ka＜0，kb＜0，kc＜0。在验证时采用文献[44]中的实验数据进行比较，在23～725 ℃、1900～3700 s−1范围内最大误差均小于15%。

在温度高于TC4 钛合金再结晶温度时，材料会发生软化现象。针对这一现象，从功热转换和能量转换的角度，对钛合金TC4 在高温条件下应力-应变曲线呈现下降的趋势进行解释。在修正时，引入单独的温度函数来进行修正，这类函数选取再结晶条件下的温度和流动应力作为参考值，修正后模型的预测误差均小于30%。

3.2 基于竞争机制影响修正

在高温、高应变率的切削加工中，应变与温度之间的耦合效应非常显著，应变硬化和动态再结晶引起的软化会形成竞争机制，经典J-C 模型很难准确预测机械加工过程中常见的锯齿形切屑形成的绝热现象[46]。胡绪腾等[33]发现在102～104s−1的应变率范围内，TC4 钛合金在室温和高温下的应变率敏感性存在差异，室温下的应变率敏感性明显大于200 ℃、400 ℃的应变率敏感性。但应变率-温度耦合效应对本构模型的影响小于应变-温度耦合现象。

侯鑫[47]发现TC4 钛合金在高温、高应变率的加载条件下，当加载温度低于100 ℃时，J-C 模型能够准确地预测材料的流动应力。当加载温度高于200 ℃、应变大于0.1 时，J-C 模型所预测的流动应力值高于实验值，且随着应变的增加和温度的升高，差值逐渐增大，最大差值约为100 MPa。选取应变率为104s−1，温度范围为25～600 ℃的流动应力数据进行定量分析，构建了变形温度与应变硬化率之间的指数模型，得到的修正本构模型如式（23）所示：

式中：m1为应变-温度敏感系数，描述应变和温度的耦合效应；m2为修正模型的温度敏感度指数。修正后的本构模型在应变0.05～0.25、温度25～600 ℃范围内流动应力值与实测值符合度较高，应变硬化率与实测应变硬化率一致。且修正前后的最大相对误差，由原先的10.43%下降至4.19%。

Seo 等[48]开发了高温SHPB 测试系统，使用两个带有两个卤素灯的椭圆辐射加热反射器解决测量试样温度的问题。为了确定真实的流动应力与真实的应变关系，以200 ℃的间隔和1400 s−1的应变速率从室温到1000 ℃进行测试。实验数据拟合的J-C 模型适合应用于TC4 钛合金在再结晶温度附近的动力学行为的表述。张铭等[49]对Seo 等[48]基于分离式霍普金森压杆实验得到的数据进行分析，发现当加载温度达到900～1000 ℃时，TC4 钛合金的流动应力急剧下降，J-C 本构模型的预测误差率达到了70.30%。在修正时综合考虑应变硬化和动态再结晶导致的应变软化的影响，以在结晶温度TC为分界点，建立了分段的本构模型，修正后的本构方程在不同温度下的误差均在7.92%以内。本构模型如（24）式所示：

式中：r为表征应变硬化与温度的耦合效应的修正系数；（σf）bc为再结晶之前的流动应力；（σf）ac为再结晶之后的流动应力。

尹浩等[50]开展了切削速率为70～150 m/min的TC4 钛合金切削实验，利用扫描电子显微镜和X 射线衍射仪进行观察和相变分析，发现TC4 钛合金的X 射线显示材料的硬化会使 得流动应力呈现一个波谷值，该波谷值通常低于材料动态回复过程中的饱和值。在该临界值之后，随着应变的增大，材料的流动应力存在下降的趋势。不同温度下α 相和β 相所占比例会发生变化，在该切削条件下β 相占比始终小于30%，因此修正时仅考虑了α 相的影响，如式（25）所示：

式中：d为α 相晶粒的尺寸；κ和a是考虑了材料α 相和拉伸性能影响的常数。最终得到的仿真结果和实验结果之间最大误差不超过10%。Chen 等[51]根据经典J-C 模型的流动应力硬化速率计算结果和显微观察，将104s−1、500 ℃设定为临界条件，针对于依赖温度的硬化效应进行了修正，如式（26）所示：

式中：T0为500 ℃。在温度高于500 ℃时，J-C 模型的平均标准偏差为55.6 MPa，而J-C 修正模型的平均标准偏差分别为42 MPa。J-C 模型预测的流变应力在700 ℃、900 ℃时相对误差大于10%，在应变为0.12 和0.14 时，误差达到25%；而J-C 修正模型的相对误差小于5%。由于J-C 修正模型在温度高于500 ℃时的加工硬化速率较小，其预测结果更接近实验结果。

综上所述，经典J-C 模型在温度高于200 ℃时的大应变条件下，预测误差会逐渐增大。针对这一现象，已有学者建立了适用于TC4 再结晶温度附近的J-C 修正模型。然而在该温度条件下，应变硬化和动态再结晶引起的软化会形成竞争机制。结合扫描电子显微镜和X 射线衍射仪进行观察，可将再结晶温度作为竞争临界点来判断该实验条件下TC4 的状态，建立分段本构模型。除此之外，也可根据流动应力硬化速率的结果，选取临界值条件的温度对应变硬化项进行修正，消除应变硬化对温度的依赖。

4 发展趋势

TC4 钛合金动态本构模型是研究动态力学性能基础，也是进行高速切削仿真的主要依据。在高速切削时本构模型的拟合中，模型在高温、高应变率条件下的预测精度以及模型的构建方法是当前研究的重点问题，具体研究方向如下：

（1）本构模型参数的拟合算法研究。优选遗传算法进行拟合，可以提高本构模型参数的预测精度[48,52-53]。鲁世红等[52]采用自适应遗传算法拟合J-C 本构模型参数，利用ABAQUS 软件进行TC4高速正交切削过程的模拟，结果表明在1200～4000 s−1、293～873 K 的实验条件下，最大相对误差为6.15%，最小相对误差为−3.48%。侯鑫[47]对比了粒子群优化算法和线性回归法的拟合结果，取应变率为104s−1、温度为25～600 ℃的实验数据进行仿真。结果表明采用线性回归法所参数计算出的流动应力最大相对误差为10.43%，而采用粒子群优化算法所得参数计算出的流动应力最大相对误差为44.39%。对本构模型进行修正后，利用线性回归法再次拟合J-C 修正模型参数，得到的预测值与实验值的最大值相对误差为4.19%。Gao 等[54]则认为单独拟合确定的参数不是整体上的最优解，因此采用全局遗传算法和局部算法相结合，保证本构参数在其理论允许范围内为全局最优解。对比该模型在2000 s−1应变率下预测能力，均优于ZA 模型与J-C 模型。

（2）基于切削实验的本构模型构建。目前拟合本构模型时的实验条件有所限制，无法真实还原实际加工条件，得到的实验数据与真实数据之间可能存在误差。在进行本构模型的修正和参数拟合时，会因为实验数据的偏差而产生一定误差。

杨勇等[55]开展了SHPB 实验和直角铣削实验，根据正交切削理论建立剪切区内应力、应变、应变率、温度以及二维切削力的数学模型，以剪切区长度和厚度比值为迭代变量进行本构模型的建立。所得到的模型预测值与SHPB 实验值之间的平均误差为14.3%；与直角铣削实验的应力预测值之间的平均误差为9.5%。李川平[56]开展了正交切削实验，测量了不同切削速率下的切削力，并将刀具前刀面和切屑之间的摩擦系数作为有限元模拟的摩擦系数，在有限元中进行迭代分析，从而获得J-C 本构参数。将参数带入仿真，结果表明计算所得主切削力与实验测量值平均误差为12.35%；进给力的平均误差为23.19%。李新建等[57]发现常规材料性能测试所获得的模型参数不能准确地描述材料在高速切削中发生的塑性流动行为，所以采用响应曲面近似法和多目标优化方法进行优化，并建立二维正交切削有限元模型进行仿真。仿真结果表明，使用常规本构模型参数仿真得到的剪切带间距、齿根高、平均切削力的误差在20%以上，而优化后的仿真结果误差均小于6%。后续研究中可以采取加工实验和计算机优化协同作用的方式来优化本构模型，使模型仿真结果更加精确[26]。

（3）复合动态本构模型。在进行TC4 钛合金高速切削本构模型的拟合时，可将众多因素结合起来考虑，如将唯象模型与物理学模型相结合、将强度模型与失效准则相结合，提高预测精度。

Lin 等[26]通过考虑应变、应变率和变形温度之间的相互影响，将J-C 模型的屈服和应变硬化部分与Z-A 模型的温度和应变率部分相结合，提出了JC-ZA 组合模型。得到的预测结果与实际的流动应力最大误差为1.217%，最大标准差为4.281%。李云飞等[24]基于细观塑性变形机理和热激活位错动力学理论，综合考虑实验温度、应变率、应变量等宏观因素，以及晶粒大小、点阵类型、原始位错分布和种类、动态回复和再结晶、变形激活能、金属类型等微观因素的共同影响，提出新的黏塑性动态本构模型，其预测结果优于单一的唯象模型和物理学模型。聂蕾等[58]将材料的宏观力学行为与显微组织演化过程联系起来，经编程算出800～1000 ℃范围内流动应力、再结晶晶粒尺寸和再结晶体积分数的预测值，与实验结果对比相对误差在15%以内。周琳[59]提出了由强度模型和失效准则组成的动态本构模型，并将预测结果与不同加载条件下的实验数据进行对比，从应变率效应、温度效应、失效准则验证了模型的合理性和准确性。从长远来看，TC4 钛合金高速切削本构模型将向综合考虑宏、微观参量，结合多尺度效应的方向发展。但宏、微观参量之间的联系仍然是研究难题之一[40]。

5 结论

（1）塑性变形时，TC4 钛合金内部组织将发生变化，晶粒沿着变形最大的方向被拉长，相互之间产生剪切滑移，从而导致晶格扭曲、畸变，发生硬化现象。在高速切削过程中，切削会带走大量热量。当切削速率高于250 m/min，TC4 钛合金的切削变形区可能会达到相变温度，发生动态再结晶软化。因此在高温、高应变率时会发生应变-应变率-温度耦合。

（2）J-C 模型对TC4 材料晶格无明确要求，但忽略了TC4 钛合金高速切削时的应变-应变率-温度之间的耦合现象。Z-A 模型及其修正模型预测时流动应力对应变的依赖性不受温度和应变率的影响。Bammann 模型可使用最大等效塑性应变失效准则删除失效单元，但无法准确确定损伤演化指数，只能采用试凑法。准静态条件下TC4 钛合金相变后的Z-A 模型的拟合精度高于J-C 模型；应变率在500～10000 s−1条件下，J-C 模型总体的拟合精度高于Z-A 模型，且随着温度的升高，拟合误差整体呈现增大的趋势。与Bammann 模型相比，J-C 模型在塑性阶段前期拟合精度高，而Bammann 模型在塑性阶段后期拟合精度高。

（3）经典的J-C 模型难以准确描述复杂的热-力耦合过程。基于温度影响修正的J-C 模型，通过引入温度函数，探究温度引起的热能与变形能之间的关系。可实现应力-应变曲线在塑性阶段呈下降趋势，减小因材料热软化对预测精度带来的影响。基于竞争机制影响而修正的J-C 模型，结合显微组织观察，以再结晶温度为临界条件，探究了应变硬化、应变率硬化与热软化之间的动态关系，可提高在再结晶温度附近的预测精度。修正后的J-C 模型与经典J-C 模型相比，预测误差均有所减小。

（4）TC4 高速切削的本构模型的构建是重点的研究方向，旨在构建出利用于在高温、高应变率条件下的预测。构建复合本构模型是表述TC4 钛合金动态力学性能的发展方向，在构建时可从多重角度考虑，如宏观和微观相结合，唯象模型与物理学模型相结合等。同时，将切削实验与计算机协同工作来实现本构模型的优化，采取全局遗传算法，得到本构模型参数的最优解。