以形助数 推算等式

浙江杭州市萧山区贺知章学校（311203） 张芳苹

一、研究缘起

图形等式推算是解决问题的一种重要策略和方法。为了解学生对图形等式推算的掌握情况，笔者对本校404 班全体学生进行了测试，得到以下结果：

测试题1：35×□+300=720。该题是简单、明确的图形等式，学生基本会运算。

测试题2：15×□=12×（□+17）。该题属于较复杂的图形等式，不能简单地用四则运算的关系解决，所以学生都束手无策。

测试题3：A、B 两市相距180 千米，甲、乙两车同时从两市出发，相向而行。甲车每小时行35 千米，3 小时后两车相遇。问乙车的速度是多少？对于该题，没有学生用图形等式解决。

产生以上现象的原因有三点。①认识不深。学生对于图形等式推算的重要性认识不深，主动运用的意识更是薄弱。②审题不细。学生在搜集信息、处理信息、整合信息方面的能力较弱，包括读题、分析数量关系等，没有理解题意，就不会列图形等式。③方法单一。图形等式推算已成为学生的一种心理负担，不少学生只会对两步以内、简单的图形等式进行逆运算，碰到需要转化、合并的图形等式时，不知如何下手。因此，学生在解决问题时更不会选择图形等式推算这一方法。

笔者认为，列图形等式有助于学生厘清思路、分析数量关系、化抽象为形象，从而解决问题，发展数学逻辑思维。但在日常教学中，图形等式推算这一方法没有引起教师的足够重视。

二、实践研究

学生学习数学的过程是循序渐进的：了解、理解、掌握、运用。笔者遵循这一规律，在图形等式推算的教学中，分四个步骤教学：认识、学会、运用、渗透。

1.思维引领，认识图形等式推算

含有图形的等式推算在教材的各个年级都会出现相应的思考题，如“3+■=5”“36÷■=4”“3×4+☆=24”，对于这样简单的图形等式，四年级学生一般能够利用图形和已知数的关系求出图形的值。如果仅是将这类题当作逆向思维习题训练，那么题目的其他价值就没有体现出来。故教师需要串联知识板块，引领学生意识到图形等式推算在解决实际问题时的独特价值。

（1）深入挖掘旧知，认识图形等式推算

从低学段开始，学生已习惯直接得出结果的算式，不会列图形等式，更没有列图形等式的意识。教师不仅要告诉学生，解决应用题可以用图形等式推算，还要教学方法的原理及应用步骤。因此，笔者首先带领学生认识图形等式推算。

【案例1】认识图形等式推算

（教师出示“3+■=5”“36÷■=4”“3×4+☆=24”）

师：同学们见过它们吗？它们有什么特点？

生1：都用符号代表数字。

师：很好，再找一找，还有什么共同点呢？

生2：都有等号。

师：这样含有等号的式子叫等式。像这样有图形的等式，你们觉得应该取个什么名字？

生（齐）：图形等式。

师：接下来请大家算一算图形等式里的图形都代表数字几。

（学生回答出分别是2、9、12）

师：我们把这样求出图形等式中图形所表示的数的过程叫图形等式推算。

让学生在旧知的基础上提炼本质，明确图形等式和图形等式推算的概念，认识到图形等式推算就是求出图形等式中图形所表示的数的过程，在不断进行巩固训练的基础上，加深学生对概念的理解。

（2）观摩优秀案例，打破学生思维定式

在图形等式推算的练习中，部分学生觉得图形等式推算换汤不换药，无非就是求未知数。此时，利用优秀的案例让学生重新认识图形等式推算是十分必要的。

将常见的图形等式推算运用到行程问题中，是学生没有尝试过的，他们不免充满了陌生感。这时，用简单易懂的案例介绍图形等式推算的方法，鼓励学生多接触，学生对于图形等式推算就不那么陌生了。而用稍复杂的案例能让学生对图形等式推算产生一定的兴趣，当用图形等式推算解决了难题，一道难题被解决的喜悦往往能培养出学生对图形等式推算的好感。

2.有效审题，学会图形等式推算

尽管有的学生基础知识掌握得很好，但如果不会审题、看不懂题意，题目还是解不出来，更谈不上什么教学效果。因此，认真审题、能准确把握题目中有价值的信息，显得尤为重要。

审题步骤可分为初读、细读、精读、复读。笔者认为这是对数学信息的搜集、整合、概括、再思考的过程。教师要引导学生结合题中重点词句理解题意、借助图形与一定的方法辅助解决问题，从而学会图形等式推算。

（1）理解重点词句

课堂上，经常能听到教师问“你得到了哪些数学信息”后，学生仅是完整地将题目读一遍。数学信息确实在题目中，但它们隐藏在重点词句里，如行程问题中常见的相对、相向、相背、相遇、相差、同时、同向等词语，抓住这些关键词，往往能顺势把题意转化成图形等式。

【案例2】把题意转化成图形等式

出示题目：两地相距270 千米，甲、乙两车同时从两地相对开出，1 小时后相遇。已知甲车的速度是乙车的1.5 倍，求甲、乙两车每小时各行多少千米？

师：同学们，读完后，你划出了哪些重点词句来帮你理解题意？

生1：“同时”“相对”“相遇”。

生2：“甲车的速度是乙车的1.5倍”。

师：很好，我们来分析一下这句话。

（板书：如果乙车速度=每小时行□千米

甲车的速度是乙车的1.5倍

甲车的速度=□×1.5）

师：现在，甲乙两车的速度都可以用含□的式子表示出来，那么怎么列等式呢？

生3：甲乙两车行的路程加起来等于两地间的距离，列式□+1.5×□=270。

师：解答得很棒，同学们，这就是我们列出来的图形等式。

（2）培养画图意识

【案例3】认识画图的重要性

题目：甲、乙两车同时从两地出发，相向而行。已知甲每小时行45千米，乙每小时行32千米，相遇时甲车比乙车多行52千米，此时过了几小时？

师：谁来说说该怎么列图形等式？

生1：假设过了★小时甲乙两车相遇，由于甲车每小时比乙车多行45-32=13（千米），过了★小时甲车比乙车多行13×★千米，所以13×★=52。

（生1说完后，很多学生摇头表示不明白）

生2：老师，我知道了，我能把这句话表述清楚。先画图（如图1），表示过了★小时甲乙相遇。等量关系：甲行的路程-乙行的路程=52 千米，即45×★-32×★=52。

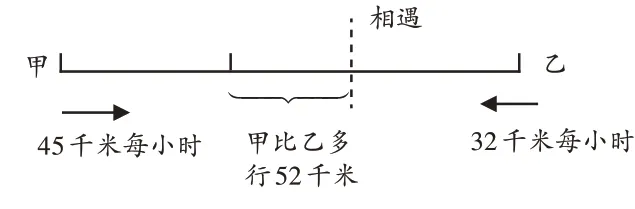
图1 甲乙两车行程示意图

培养学生画图意识，需要教师适时加以引导。讲课中，教师要少画图，鼓励学生自己动手画一画、说一说，让学生发自内心体会到画图能将问题简单化，有助于理解题意、快速准确地列出图形等式。

（3）学会推算等式

一步到位的图形等式，学生是容易完成的。故重点和难点是两步甚至三步以上图形等式推算。

【案例4】图形等式推算方法

出示：35×□+300=720。

师：图形等式中的运算顺序同一般数学算式，所以某一步中含有图形的，需要看作一个整体。解这个算式，把35×□看作一个整体，想35×□等于几？一个加数=和-另一个加数，得到35×□=420，

题目转化为一步图形推算。出示：120-◇×5=30。

生1：我把◇×5 当成一个整体，减数=被减数-差，◇×5=90，◇=18。

出示：40×■+60×■=2400。

生2：利用乘法分配律，转化成（40+60）×■=2400，就能很快算出■。

出示：2×★+1=★+3。

生3：这个图形等式可以通过两边同时减1 转化成2×★=★+2。

师：非常好，那现在怎么求★呢？

（生3摇摇头，表示没有办法。）

师：一边有图形的要先合成一处，那两边有图形的首先要转化成只有一边有图形，两边同时减去一个★，得★=2。

师：那能解“2×★-3=★-1”吗？

生4：等式两边都先同时加上3，转化成“2×★=★+2”，就和前面那题一样啦！

通过实践让学生认识到等式一边有图形的要先合成一处，等式两边都有图形的需要转化为只有一边有图形，利用四则运算不断求解二步以上的图形等式。

3.举一反三，运用图形等式推算

学习了图形等式推算这一解题策略后，学生碰到各种行程问题，要第一时间辨别该题适不适合用图形等式推算来解决，要根据等式选择合适的方法。

（1）辨析题型

【案例5】讨论图形等式推算的题型特点

师：同学们，你们认为哪些行程问题可以不用图形等式推算来解？

生1：我认为能直接求出来的题可以不用。

师：反之，不能直接求出来的题可以用图形等式推算对吗？还有没有可以不用图形等式推算来解的？

生2：简单的题可以不用。

师：你的意思是复杂的题可以用图形等式推算，但是简单或复杂因人而异。其实“直接求出来”与“简单”是同一个意思。我们说一步到位的题、正向思维运算的题可以不用图形等式推算。

出示案例3 的变式：甲、乙两车同时从A、B 两地出发，相向而行。已知甲车每小时行45 千米，乙车每小时行32 千米，相遇时甲车比乙车多行52 千米，问A、B两地相距多少千米？

生3：这个题可以先用图形等式推算，假设相遇时间为★小时后，求得★是4 小时，A、B 两地的距离是45×4+32×4=308（千米）。

显然，已有一部分学生意识到图形等式推算在解决较复杂的行程问题时的重要性，会选择图形等式推算来解决。

（2）建构模型

在一定的巩固训练基础上，学生对用图形等式推算解决行程问题已有了经验。此时，通过一类图形等式推算总结出一类代数模型的求解方法（见表1），能为以后的方程学习做铺垫。

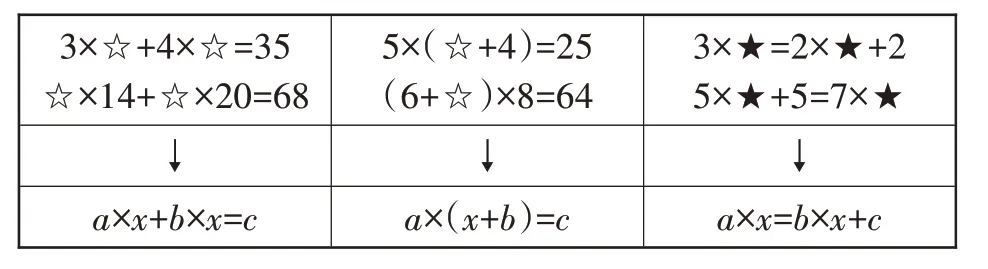
表1 由图形等式到方程

随着图形等式增多，代数模型呈现形式变得多样，但在一系列转化合并后仍会回到最基础的代数模型。另外，教师还可鼓励学有余力的学生探究三步以上图形等式的代数模型求解方法。

4.发散思维，渗透图形等式推算

图形等式推算作为一种解题策略，不仅能解决行程问题，还能解决其他类型的问题，如解决鸡兔同笼问题、求长方形长和宽等。在教学中不要单纯地就题论题，而要把学生已学的方法渗透到多种题型中去，一方面巩固图形等式推算的训练，另一方面使学生意识到要融会贯通新方法，发散思维地运用它。

三、实践反思

图形等式推算在问题解决中具有十分重要的作用，它生动形象地将复杂的数学问题变得简单明了。在实践研究过程中，笔者看到学生运用图形等式推算解决问题的意识增强，对题目的辨析思考能力增强，学生运用图形等式推算解题，大大提高了他们的问题解决能力，同时也大大提高了课堂学习效率。然而，图形等式推算作为解决问题的一种策略和方法，与五年级“等式性质”不同，那么教师在教学中应如何引导学生灵活选择这一策略方法？影响学生运用这一策略的因素又有哪些？这一系列的问题都值得继续思考。