时空环境因素对无信号交叉口事故严重程度的异质性影响

陈 钦

(江苏都市交通规划设计研究院有限公司,江苏南京 210001)

据世界卫生组织(World Health Organization)报道,道路交通事故已成为人类非正常死亡的主要致因[1]。根据事故伤害的严重程度,可以将道路交通事故分为死亡事故、重伤事故、轻伤事故和仅财产损失事故4类,探明不同伤害程度事故的发生原因对预防事故发生、降低人身伤害、减少财产损失意义重大。

围绕人、车、路、环境等不同角度,国内外学者已经开展了大量的理论研究和实证研究,分析驾驶行为特性[2]、驾驶员属性(性别、驾龄等)[3]、车型[4]、车辆速度特性[5]、道路特征[6]、车道宽度[7]、天气[8]、交通流特性[9]等因素对事故严重程度的影响效能。但是,即便是相同的因素,它们在白昼和夜间对行车安全的作用效果也存在显著异质性,例如夜间时段不良光照条件对驾驶员视距的限制比白昼时段更加严重,这将会显著加剧驾驶员正确判断安全跟车距离以及安全车速的难度,同时让驾驶人难以明晰路肩位置和道路曲率,威胁行车安全。因此,以事故率普遍较高的无信号交叉口为例,采用数理统计的手段探查白昼和夜间时空环境因素对事故严重程度的贡献差异,捕获影响因素在时间维度上的不稳定特征具有重要意义。

目前国内外研究学者用于探究事故严重程度影响因素问题的最有效方法是离散选择模型。常用的离散选择模型大多基于传统Logit模型结构形式,例如SZE等[10]综合考虑区域人口数量、碰撞、建筑环境、道路几何以及交通条件等多维特征,构建二元Logit模型用于确定死亡事故和受伤事故的影响因素差异。林庆丰等[11]则在道路环境因素的基础上,将驾驶人年龄因素加入多项式Logit模型,分析了不同形态公交车事故中严重程度影响因素的异同性。但是传统Logit模型的基本假设是将所有参数均视作固定参数,即默认因素对严重程度的影响机理始终是无变化的。这一假设忽视了影响因素的时空变化特性,因此往往无法深入剖析影响因素的潜在关系。针对此类异质性问题,研究人员从参数的角度出发,允许模型参数在一个分布区间内变化(通常为正态分布),构建了随机参数模型[12]。WU等[13]采用随机参数Logit模型分别量化了驾驶员行为、天气条件、环境特征、道路几何特征和交通组成对多车事故和单车事故的影响。BEHNOOD等[14]同样采用随机参数Logit模型研究了全球经济衰退3个阶段中,事故造成行人伤害严重程度的影响因素差异。随后,随机参数的均值和方差异质性也引起了研究人员的重视,有学者提出了考虑均值和方差异质性的随机参数模型。基于此模型,YAN等[15]构建挖掘恶劣天气条件下事故严重程度影响因素的时空不稳定性;SERANEEPRAKARN等[16]研究了涉及混合动力车辆的事故严重程度影响因素;宋栋栋等[17]分析了驾驶人、道路和环境潜在因素对城市道路事故严重程度的异质性影响;潘义勇等[18]重点讨论了建成环境对老年人在交通事故中遭受伤害等级的影响因素。

综上所述,国内外研究人员在研究事故严重程度影响因素方面已经取得了许多成果,但是仍然缺乏对建成环境和天气环境因素的综合探讨,而且对时空因素的影响考量较少。本研究以美国西南部某州的事故数据为基础,构建均值和方差异质性的随机参数Logit模型,重点考虑影响因素的时空不稳定性,根据模型参数估计和边际效应分析结果,深入探讨时空环境对城市道路无信号灯交叉口路段的事故严重程度的异质性影响机理,并解析这些特征之间潜在的异质交互作用,以期为车辆被动安全系统的设计提供理论依据和参考。

1 建模方法

1.1 考虑均值和方差异质性的随机参数Logit模型

笔者选择采用考虑均值和方差异质性的随机参数Logit模型来分析无信号交叉口昼夜时段事故严重程度的影响因素,该模型的效用函数如式(1)所示。

Sij=βiXij+εij,

(1)

式中:Sij表示事故j的伤害严重程度为等级i的效用函数;βi为待估参数的向量;Xij为事故j中伤害严重程度为i的解释变量的向量;εij代表服从广义极值分布的误差项。根据效用函数构建的多元Logit模型[19],如式(2)所示。

(2)

式中:Pj(i)表示事故j严重程度为i的概率;I为所有事故严重程度的集合。标准的多元Logit模型中假设每个解释变量对每起事故严重程度的影响是固定不变的,但是在实际事故中解释变量的影响会因为事故的差异而不同。因此为了解决事故中由于未观测到变量引发的异质性问题,在模型中引入均值和方差异质性向量,其表达形式如式(3)所示。

βi=β+θijZij+σijexp(φijWij)vij,

(3)

式中:β表示待估参数的均值;Zij为事故j中存在的均值异质性向量,用于捕捉均值异质性;θij则为其对应估计参数的向量;σij为βi的标准差;Wij为方差异质性向量;φij为Wij对应的待估参数向量;vij为误差项。此时可构成考虑均值和方差异质性的随机参数Logit模型,如式(4)所示。

(4)

式中:f(β|φ)为β服从某种分布的概率密度函数,根据以往研究的成果,刻画事故严重程度一般采用正态分布的形式[20];φ表示刻画该分布的预定义参数向量。由于考虑均值异质性的随机参数Logit模型为非闭式积分,无法求解出闭式解析解,因此,采用500次Halton序列抽样的模拟极大似然估计法(simulation maximum likelihood estimation, SMLE)对参数进行估计。

1.2 解释变量的边际效应

模型中解释变量的估计参数无法直接反映其对事故严重程度的影响程度,因此选用边际效应评价方法来分析每个解释变量对结果的影响程度。离散变量和连续变量的边际效应计算公式如式(5)和式(6)所示[21-22]。

(5)

(6)

式中:Ed和Ec分别为离散变量和连续变量的边际效应;Ed刻画的是离散变量从0变为1时,对应伤害严重程度概率变化的百分比;Ec为连续变量变化1%时,对应伤害严重程度概率变化的百分比。

2 数据描述

事故数据来源于美国西南部某州2016年7月至2020年12月的历史事故数据统计,剔除统计数据缺失值和数据异常值,筛选得到城市道路无信号灯路段事故5 956起,以每日6:00—18:00为白昼时段,其余时间为夜晚时段的方式划分,得到白昼时段事故3 519起,夜间时段事故2 437起,根据造成的人员伤亡和财产损失后果,事故被划分为4个等级,分别是仅财产损失事故、轻伤事故(非失能性损伤)、重伤事故(失能性损伤)和死亡事故,4类事故分别占比4.89%,76.73%,12.99%和5.39%。

以无信号控制交叉口路段的交通事故为研究对象,将事故划分为白昼事故和夜间事故进行分析,重点探究时间、空间特征和环境因素对事故严重程度影响的异质性,主要选取了周时间(星期一至星期日)和季节(春季至冬季)[15]、道路空间因素(道路类型、侧向以及周围交通设施和建筑设施情况等)和环境因素(气象条件、天气状况、能见度、风速等)[23]4个方面的因素。其中,道路空间因素中除了“事故发生于道路左侧”“事故发生于道路右侧”之外,均为独立离散变量。气象条件不仅划分为“良好天气条件”和“恶劣天气条件”,同时还划分了具体的气象分类,以此来量化气象条件对事故严重程度的影响。具体信息如表1和表2所示。

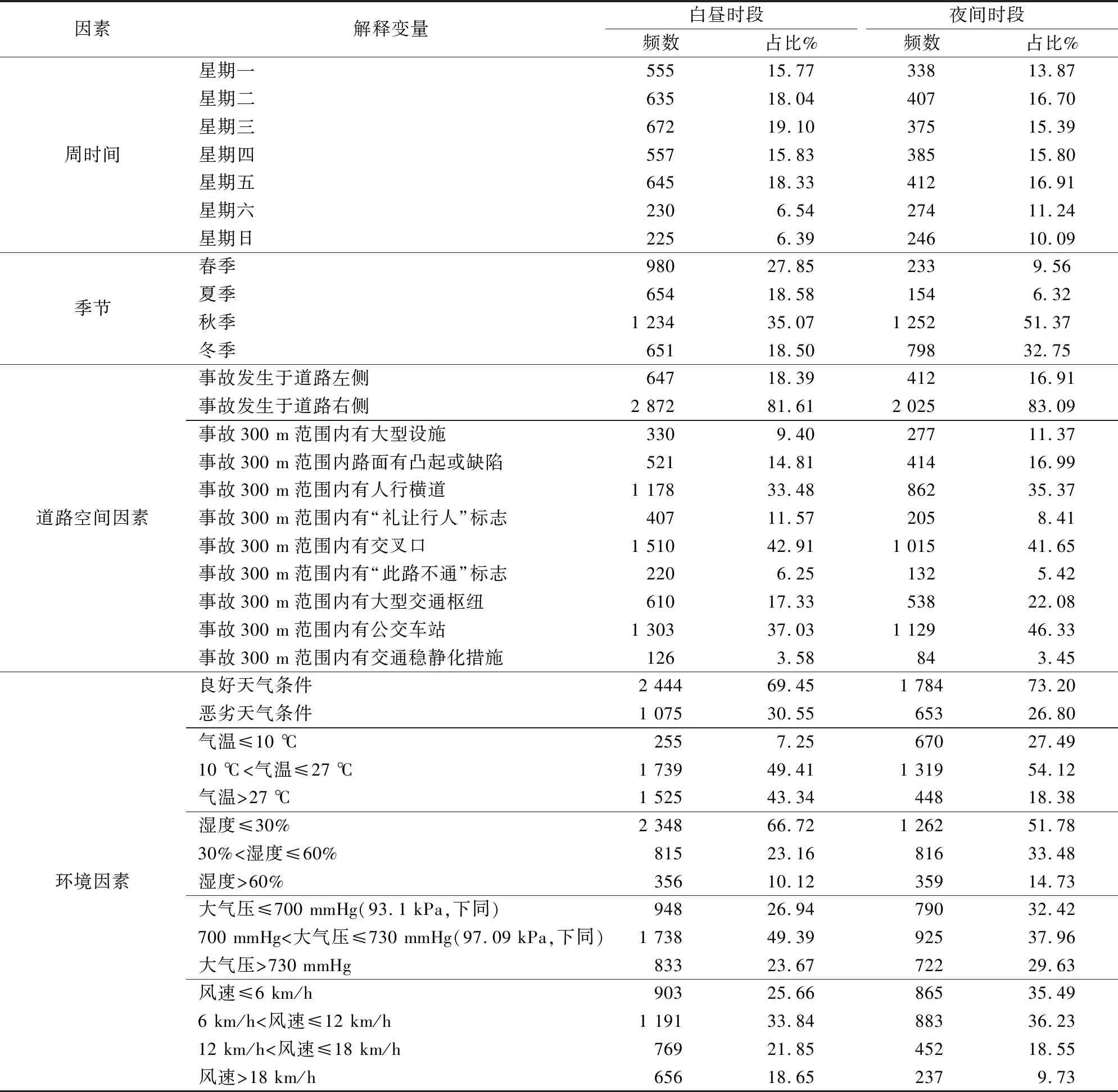
表1 事故数据的描述性统计(离散变量)

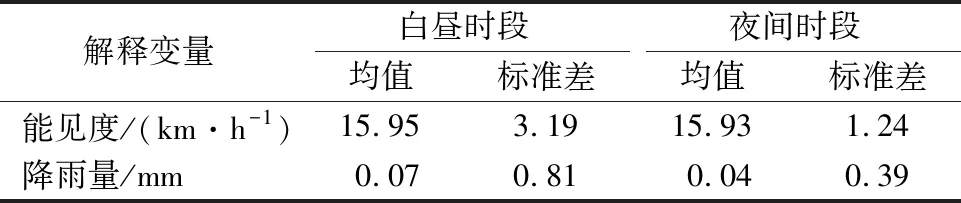
表2 事故数据的描述性统计(连续变量)

3 模型结果分析

无信号交叉口白昼和夜间的事故严重程度建模对比结果如表3和表4所示,其中MNL表示多项式Logit模型,RPL表示随机参数Logit模型,RPLM表示考虑均值异质性的随机参数Logit模型。由于在建模过程中并未捕捉到模型的方差异质性,因此最终模型退化为考虑均值异质性的随机参数Logit模型。拟合优度较好的模型具有更低的赤池信息量准则(akaike information criterion,AIC)值和更高的对数似然值和麦克法登伪R2(McFadden PseudoR2,以下简称伪R2)。根据模型标定的结果,RPLM在白昼事故和夜间事故拟合过程中的AIC值低于MNL和RPL模型,而对数似然值和伪R2则高于前两者。采用χ2检验的方法来验证是否有必要采用更复杂的考虑均值异质性的随机参数Logit模型,χ2检验结果表明在95%以上的置信度水平下,可以拒绝考虑均值异质性的随机参数Logit模型与其余2个模型性能相同的原假设。因此结果分析以RPLM的结果为基础。

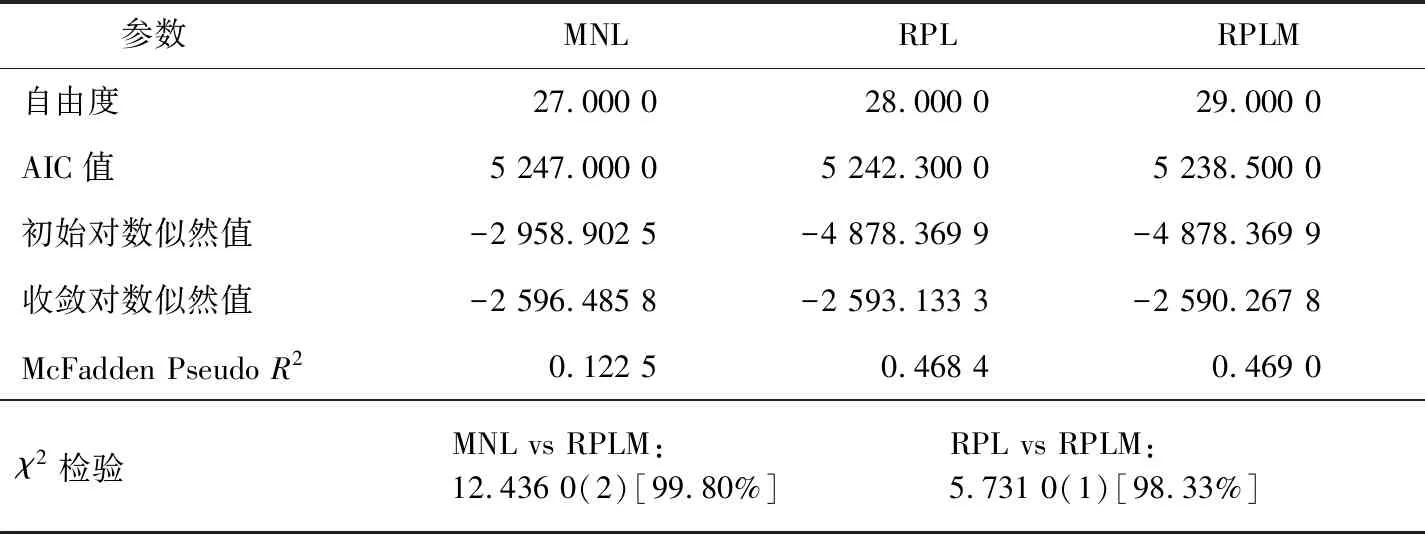
表3 白昼时段事故的模型对比结果

3.1 随机参数分析

图1和表5、表6中:[F]表示死亡事故,[S]表示重伤事故,[M]表示轻伤事故,[N]表示仅财产损失事故。白昼事故和夜间事故的模型参数估计结果见表5和表6,白昼事故模型中,只有在事故严重程度为重伤事故时,“夏季”变量被识别为随机变量,服从均值为-3.017、标准差为3.511的正态分布。而在夜间事故模型中,轻伤事故的“夏季”变量和死亡事故的“恶劣天气条件”变量均被识别为随机变量,分布服从均值为-1.246、标准差1.968和均值为2.393、标准差为2.992的正态分布。为了更直观地反映随机参数的影响机理,绘制的随机参数正态分布曲线如图1所示。从正态分布图可以看出“夏季”变量有19.51%的可能性会增加在白昼事故中造成人员受重伤的概率,同时“夏季”变量还有26.32%的可能性会增加在夜间事故中造成人员受轻伤的概率。此外,“恶劣天气条件”变量则有78.81%的可能性会增加在夜间事故中造成人员死亡的概率。

图1 随机参数的概率密度分布Fig.1 Probability density distribution of random parameters

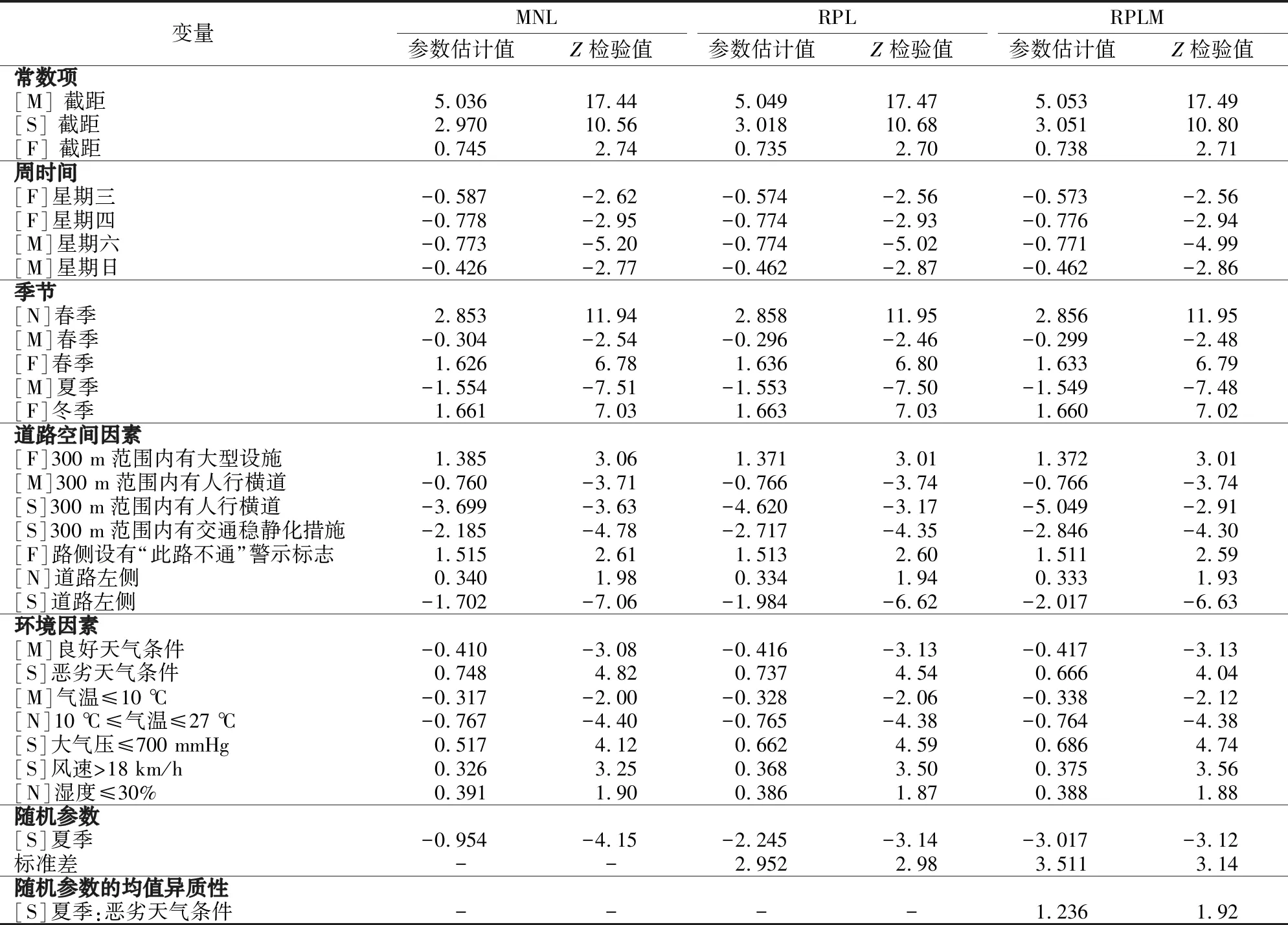
表5 白昼事故模型参数估计结果

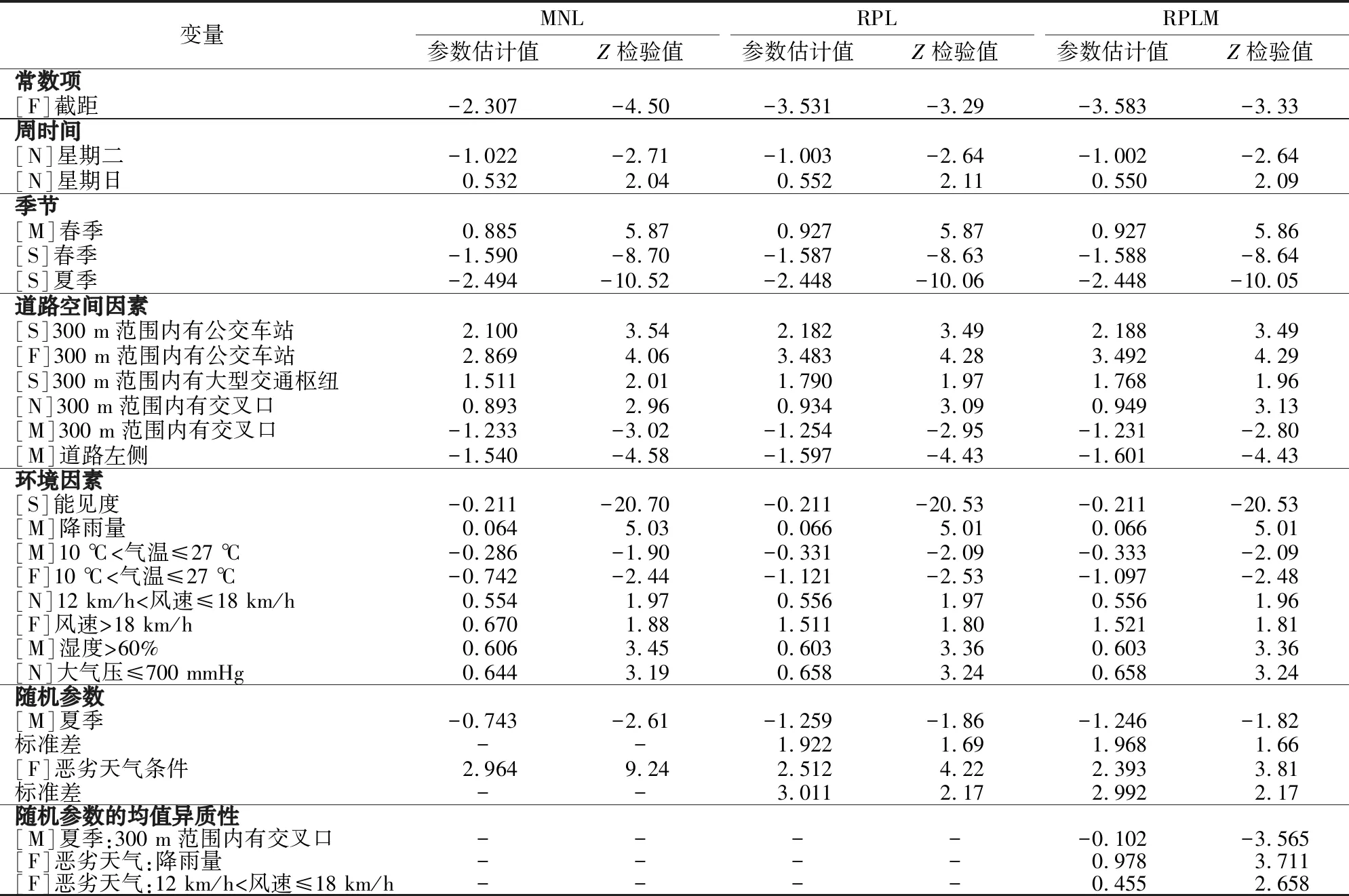
表6 夜间事故模型参数估计结果

3.2 随机参数的均值异质性分析

白昼事故和夜间事故模型的均值异质性影响分别见表5和表6。

通过表5可以看出,在白昼时段发生的事故中,“恶劣天气条件”因素的均值异质性系数为1.236,这说明该因素会显著增加随机变量“夏季”的正态分布均值,即恶劣天气条件会增加发生在夏季白昼时段事故造成人员重伤的概率。

表6的结果反映出对于夜间发生的事故,随机变量“夏季”的正态分布均值受“300 m范围内有交叉口”这一因素的负相关影响,这意味着当夏季夜间事故发生在交叉口附近时,造成人员受轻伤的概率将会降低。值得注意的是,对另一个随机变量“恶劣天气条件”具有均值异质性影响的2个因素(降雨量,12 km/h<风速≤ 18 km/h)均为环境因素。这2个因素的特点在于更细致地刻画了恶劣天气条件的状态,并且均表现出正相关的影响关系。也就是说,对于发生在恶劣天气条件下的夜间事故,当恶劣天气条件表现为大雨或强风时,其造成人员死亡的概率增加。

4 事故影响因素分析

通过对比参数估计结果可见,除了上述随机参数和均值异质性的差异外,固定参数在白昼时段事故和夜间时段事故中也表现出明显的不同。因此对白昼事故模型和夜间事故模型均进行边际效应分析,以进一步探究影响因素对事故严重程度的实际影响效果,结果分别如表7和表8所示,若变量在某种事故中的边际效应值为正,则说明该变量会增加该种事故发生的概率,以下结果均根据表7和表8的边际效应值分析得出。

4.1 时间因素

表7中的“周时间”和“季节”的边际效应结果表明,对于白昼时段事故而言,星期三和星期四在死亡事故中边际效应值分别为-0.003 9和-0.003 6,说明星期三和星期四的白昼发生死亡事故的概率降低,而星期六和星期日在轻伤事故中的边际效应值分别为-0.010 6和-0.005 7,说明周末更不易发生轻伤事故。从事故的季节分布上来看,春季时发生死亡事故和仅财产损失事故的概率均增加,但是轻伤事故的概率则会降低。夏季的重伤事故和轻伤事故概率均有一定程度降低,而冬季只会增加死亡事故的概率。

表8中的“周时间”和“季节”的边际效应结果表明,对于夜间时段事故而言,仅财产损失事故易发生于星期日。春季会增加轻伤事故概率而降低重伤事故概率,夏季则会降低死亡事故概率。可以看出,无论是白昼事故还是夜间事故,在春、夏季节的变化性更为显著,这说明春、夏季节造成事故的影响因素以及影响因素间的交互效应更加复杂。

4.2 空间因素

表7中的“道路空间因素”边际效应结果表明,人行横道的设置会降低轻伤和重伤事故的概率,而有交通稳静化措施的道路重伤事故概率也会降低。相反发生在大型设施或设有“此路不通”警示道路的事故则有可能增加人员死亡的概率。另外,当事故发生在道路左侧时更有可能只造成财产损失。

表8中的“道路空间因素”边际效应结果表明,公交车站和大型交通枢纽附近的事故更容易造成人员重伤甚至死亡,相反交叉口附近和道路左侧的事故不易造成人员伤亡,交叉口附近多为财产损失事故。

这些现象的原因主要在于人行横道和交通稳静化设施往往会意味着道路有更多的安全保障措施,而大型设施和公交车站附近车流量较大,交通流成分较为复杂,同时设有“此路不通”警示标志道路往往是处于施工或其他不利于通行的道路状态,因此这些地方更容易造成严重的交通事故。而交叉口附近以及道路左侧的车速普遍较低,因此事故多为轻微碰撞或者剐蹭,不易产生严重的事故后果。

4.3 环境因素

表7中白昼时段事故的“环境因素”边际效应结果表明,良好的天气条件会显著降低轻伤事故发生的概率,而恶劣的天气条件则会增加重伤事故概率,这与常规的认知相符。具体来说,当气温在10 ℃以下和10～27 ℃时分别会降低轻伤事故和仅财产损失事故的发生概率。另外,较低的大气压和较高的风速都会造成重伤事故频发,而干燥的天气则会更多引发仅财产损失事故。值得注意的是,白昼时段事故中造成重伤事故概率增加的3个因素在气象学上均属于强降雨天气的显著特征,虽然本文并未对“强降雨”、“降雪”变量进行具体定义,但是根据这些量化指标依旧可以推断出,相比于降雪、低温和雾霾等天气,降雨仍是造成严重事故的主要诱因。而干燥天气下车辆部件干摩擦严重,进而造成车辆制动性能下降,动力性能减弱,即在交通流较拥堵时容易在反复的加减速操作中出现车辆剐蹭、追尾等车损事故。

表8中夜间时段事故的“环境因素”的边际效应结果表明,恶劣天气条件和超过18 km/h的强风会直接造成死亡事故的概率增加,而能见度越高发生重伤事故的概率越低。通常情况10～27 ℃时被认为是较为舒适的环境温度,这一因素会降低死亡事故和轻伤事故的概率。此外,引起轻伤事故和仅财产损失事故概率增加的因素包括低气压、12～18 km/h的风速、较多的降雨量和较大的湿度,这些因素都是伴随着大雾或者强风降雨天气的典型特征。

5 结 语

本文基于5 956起事故数据构建考虑均值异质性影响的随机参数Logit模型,通过参数估计和边际效应分析得出了时空环境因素对城市道路无信号交叉口昼夜时段事故严重程度的异质性影响,研究主要结论如下。

1)“夏季”变量的估计参数在昼夜模型中均为随机参数,并对昼夜事故严重程度均有异质性影响。“恶劣天气条件”变量仅对夜间事故严重程度存在异质性影响。同时“恶劣天气条件”变量会增加夏季白昼事故严重程度为重伤的概率,而在夏季夜间发生于交叉口附近的事故造成轻伤可能性会降低。

2)人行横道、交通稳静化设施对轻伤、重伤事故的边际效应均为负值,说明这2种设施有助于减少人员在事故中受伤的概率,大型交通枢纽以及特殊状态下的路段附近容易出现人员重伤甚至死亡的事故。

3)中低气压、高风速、高降雨量有加重事故严重程度的倾向,各类恶劣天气条件中,伴随强风或者大雾的降雨天气仍是加剧事故严重程度的主要原因。

4)时间因素上,事故严重程度在春、夏季节受不同因素影响的变化性较大,春、夏季节的影响因素交互作用更为复杂,道路使用者的出行特征变化也更具动态。

此外,本文还存在一定的局限性,例如未对不良天气条件进行明确定义,而且受样本量限制,无法探究结果在空间层面上的可转移性。因此,仍需使用更多的事故样本,进一步探索在中国独特的政策环境和交通环境下,无信号交叉口是否具备类似的特性,从而更好地优化交通安全环境。同时,未来有必要针对春、夏季节的事故严重程度影响因素作进一步分析挖掘。考虑到事故数据往往有较长的时间跨度,因此还需要针对不同年份之间事故严重程度影响因素的时变性特征进行分析,这对于改善道路交通安全具有重要意义。