基于模型剪枝动态调整压缩率的CSI反馈方法

邵 凯, 杜自群, 王光宇,3

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 教育部移动通信工程研究中心, 重庆 400065;3. 移动通信技术重庆市重点实验室, 重庆 400065)

0 引 言

在大规模多输入多输出(multiple input multiple output, MIMO)系统中,信道状态信息(channel state information, CSI)的准确性直接影响系统的整体性能,在预编码、波束赋形、信道估计和信号解调等方面发挥着极其重要的作用。在时分双工(time division duplex, TDD)制式下,下行链路的CSI可以利用信道互易性通过上行链路推测而得到[1]。而在频分双工(frequency division duplex, FDD)制式下,上下行链路呈现弱互易性,下行链路的CSI不能通过上行链路推测获得,需要在用户端获得并通过上行链路反馈给基站。由于大规模MIMO系统天线数量激增,CSI反馈机制会带来巨大的反馈开销,占用了大量上行链路时频资源,严重影响了系统性能。

为了解决大规模MIMO系统CSI反馈开销大的问题,业界对CSI反馈方法开展了广泛的研究,例如基于码本[2-4]、基于信道特性[5-8]、基于压缩感知(compressed sensing,CS)[9-11]、基于深度学习(deep learning,DL)[12-14]等的反馈方法。在基于码本的反馈中,用户和基站通过预先设定的码本,以编码的“索引”方式交流CSI信息,但码本大小随天线数成比例增加,最优码字搜索算法也会愈加复杂。基于信道特性的反馈利用大规模MIMO的信道统计特性和时域、空域等表现出的相关性进行分组处理,可以大大减少反馈信息,但在现实通信场景中,不易获取大规模MIMO系统的统计特性,限制了其实际应用。

CS方法和DL方法都致力于提取CSI特征,降低反馈信息维度。例如主成分分析(principal components analysis,PCA)方法[9]、分布式压缩感知[10]和卡洛南变换(Karhunen-Loeve transform,KLT)[11]等压缩采样类方法尝试将信道矩阵通过稀疏基变换到稀疏域,通过CS观测矩阵对信号进行压缩降维。而文献[12-14]则通过DL的方式从数据样本中提取CSI高维特征,相较于原始信道矩阵反馈开销大大减少。

在CS的方法和DL方法中,均存在信号恢复的问题。CS中常用的恢复算法有正交匹配追踪(orthogonal matching pursuit,OMP)[15]、近似消息传递(approximate message passing,AMP)[16]、软阈值迭代算法(iterative shrinkage-thresholding algorithm, ISTA)[17]等。但CS方法存在3个固有问题。首先,CS严重依赖于信道稀疏的先验假设,然而在实际情况中,信道并非是完全稀疏的,甚至还可能拥有其他不可解释的结构。再者,CS使用的随机观测矩阵不能完全利用信道内在结构,无法提取除稀疏性的其他信道特性。最后,目前的CS重构算法通常是迭代式算法,重构的速度较慢。DL方法可以通过学习网络提取信道特性,无需受先验知识的约束。文献[12]中,作者首次提出将DL应用于CSI反馈并设计了CsiNet反馈网络,在用户端使用自动编码器对信道特征进行提取,同时在基站端利用神经网络对信号重建恢复。通过扩展文献[12]的方法,文献[13]利用信道时间相关性构建循环神经网络(recurrent neural network,RNN),以解决时变信道反馈问题,同时增加了深度可分离卷积修正网络,利用上下行链路之间的相关性来减少反馈开销。

综上,DL方法在CSI反馈中发挥出日益重要的作用。但是,CS方法可以通过调整观测矩阵实现不同压缩率(compression rate,CR)的反馈,但现有的DL方法仅能以固定CR对CSI进行压缩反馈,无法依据通信场景、系统需求和频谱资源对CR进行动态调整,即针对不同的CR,必须训练和存储不同的网络模型,占用了用户设备大量的存储空间,在实际使用中灵活性较差,严重影响了DL方案的实际部署应用。文献[14]指出,高CR的信道矩阵可以由低CR的信道矩阵产生,在文献[12]的基础上通过级联全连接(fully connected, FC)层对信道矩阵进一步压缩,实现高CR反馈,并且提出了级联多(serial multiple, SM)CR反馈模型SM-CsiNet+。但级联FC层增加了模型深度,使得模型过于冗余,极易在训练过程中产生过拟合现象,且只能从低CR到高CR逐级压缩,实际使用的可操作性较差。因此,本文基于2范数模型结构化剪枝技术,提出了一种可在DL中动态调整CR的CSI反馈方案。本文主要工作如下:① 根据通信CSI信息特征,设计了残差信道特性注意(residual channel characteristic attention,RCCA)机制,并搭建了CSI反馈网络RCCA-Net。该网络由Encoder和Decoder两部分组成:Encoder在用户端提取信道矩阵内在特征并将其转换为压缩码字,Decoder在基站对压缩后的信道矩阵进行恢复重建。针对通信CSI复数特征,所设计的RCCA机制在Decoder端分两支路处理信道压缩矩阵:上支路卷积层提取相邻元素间关系,下支路利用全局平均池化(global average pooling,GAP)提取复信道矩阵所形成的两通道间的依赖关系。将RCCA级联组成多层残差(multi-layer residual, MLR)网络加大网络深度,以增强重建效果;② 在RCCA-Net基础上,本文提出了动态调整CR方案RCCA-Prune。针对不同的CR,使用2范数评估RCCA-Net Encoder端权重矩阵中各神经元的重要性,通过删除冗余神经元来动态调整CR。

1 系统模型

(1)

(2)

Hc=fen(H,θ1)

(3)

式中:fen(·)表示压缩过程;θ1表示压缩模块(编码器)的参数。

编码器将信道矩阵转换为M维向量(码字),解码器是码字到原始信道矩阵的逆变换:

(4)

式中:fde(·)表示解压缩过程;θ2表示解压缩模块(解码器)参数。结合式(3)和式(4),以均方误差(mean square error,MSE)作为度量标准,将CSI反馈过程建模为一个优化问题,用公式表示如下:

(5)

图1所示为CSI反馈系统的基本模型,由CR选择、特征提取、数据压缩、数据解压缩和特征重建等模块组成。

图1 CSI反馈系统模型Fig.1 CSI feedback system model

在用户端,首先对信道矩阵进行特征提取;根据通信场景、系统需求和频谱资源等指标,CR选择模块设置相应的CR,数据压缩模块按CR对信道特征压缩编码,经上行链路反馈至基站,解码器进行解码,重建信道矩阵。

2 解码器至基站

图2 RCCA-Net模型框架Fig.2 RCCA-Net model architecture

(6)

图3 下支路通道特征校准Fig.3 Lower branch channel characteristic calibration

首先,通过GAP计算实部虚部两通道的特征响应,得到一个C×1×1的通道维度的全局特征描述[18]。接着,通过一个1×1的下采样卷积层和ReLU(rectified linear unit)激活函数将特征描述映射为权重集合;之后,通过上采样对权重重新加权分配,卷积核大小同样是1×1,激活函数选择Sigmoid,下采样和上采样实际上是对通道特征的重新校准;最后,上下支路逐元素相乘进行信息融合,得到完整的信道特性。

(7)

3 RCCA-Prune

在神经网络模型中,通常包含有卷积层、池化层、FC层、非线性层等基本结构,通过这些基本结构堆叠,最终形成常用的深度神经网络。根据DL理论[23],神经网络中存在大量冗余的参数和神经元,参与主要计算并对最终结果产生影响的只占总数的5%～10%。模型剪枝是一种压缩模型大小和参数的方法,主要分为结构化剪枝和非结构化剪枝。非结构化剪枝方法剪掉不重要的神经元连接,会破坏原有模型结构,影响现有硬件架构对其计算过程的加速。而结构化剪枝以神经元或整个网络层为基本单位进行剪枝,剪枝后其前后特征图会发生相应的变化,但不会破坏模型结构,可以通过GPU或其他硬件来加速。经过剪枝处理的模型通常很稀疏,模型结构复杂度和参数量均会下降,可避免过拟合现象的发生,提高模型的泛化性。

剪枝过程通过定义重要性指标来剪除相对不重要的参数,如图4所示。剪枝的指标往往是启发式的,根据评估指标时所利用的信息,模型剪枝评估准则可分为数据驱动和参数驱动两类。基于数据驱动的评估准则需要利用输入数据,通常从特征层面、梯度层面和网络输出结果等方面进行分析。但由于输入数据的参与,模型剪枝过程较为复杂,计算资源和评估时间增加,导致实际使用受限。基于参数驱动的评估准则在网络结构重要性评估过程中无需依赖输入数据,常使用1范数、2范数、几何中位数[24]、批归一化层中的γ参数和谱聚类[25]等方式来评估各神经元重要性,通过预先设定的参数阈值来决定要修剪的网络结构。由于其评估过程不需要输入数据,只依赖模型本身的参数,对计算资源要求较少,非常适合成本和内存受限的用户设备部署使用。

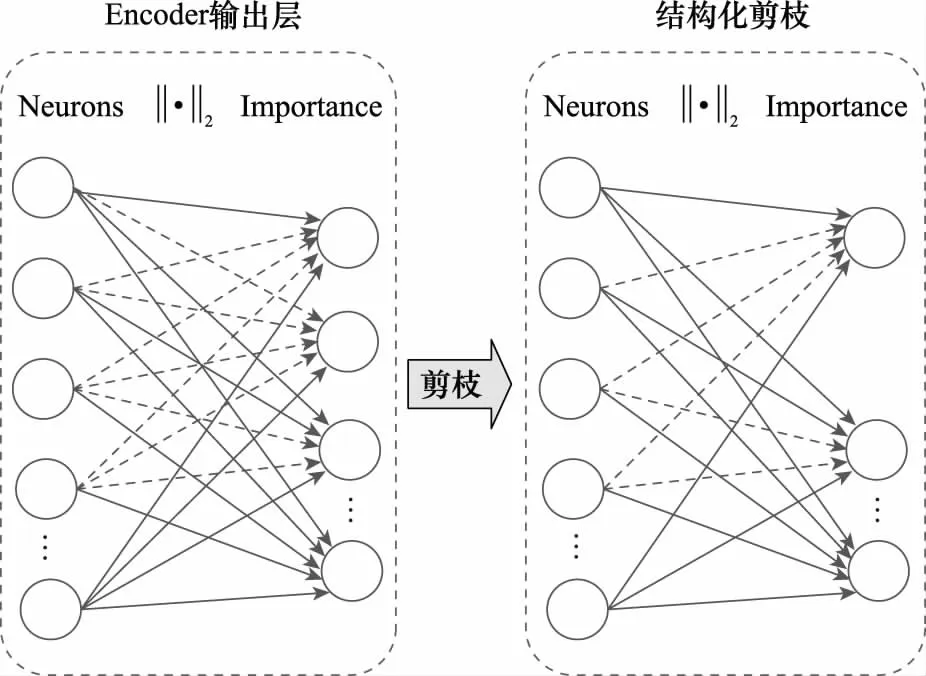
图4 模型剪枝示意图Fig.4 Model pruning framework skematic diagram

CS方法可以通过调整观测矩阵实现不同CR, RCCA-Prune的设计目的是采用剪枝方案从RCCA-Net中裁剪掉不重要的神经元以完成CR的调整,实现DL方案中对CSI信息的动态反馈。需要强调的是,模型剪枝的典型应用是减少模型参数量和计算复杂度,但在本文的研究问题中,剪枝是为了对数据进行进一步压缩,从而实现CR的动态调整。针对不同的问题,会有不同的重要性度量指标决定哪些神经元应该被裁剪,几何中位数是对欧式空间点中心的估计,一般用于卷积层的模型剪枝。本文动态调整CR主要依靠FC层的剪枝操作,故不适合采用几何中位数的评估准则。批归一化层中的γ参数是在模型训练过程中经过逐步优化获得的,训练数据集分布情况、训练轮数等都会影响γ参数,在实际情况中较难确定。谱聚类严重依赖相似矩阵和切图方式的选择,不同的参数对聚类结果会有较大影响;且聚类过程涉及大量矩阵求逆操作,计算复杂度很高。1和2范数都可作为神经元剪枝的评估准则,但1范数趋向产生少量特征,其他特征都为0,可能会使模型损失较多的有效特征,影响模型的特征表达。2范数会选择更多的特征,这些特征都接近0,实现了对模型空间的限制,通过剪枝可让模型推理更加稳定快速,避免过拟合现象的发生,提高模型的泛化能力。

图4是剪枝前后模型结构变化示意图。对于Encoder输出层中的第t个神经元,假设共有Nt条连接。每条连接以wi定义权值。

图4中以不同线型表示权值大小,线条越细,代表wi越小,虚线则表示对应的wi非常小。定义St表示第t个神经元所有连接的2范数之和,依St值对神经元按重要性进行排序。根据CR计算剪枝阈值k,将低于阈值k的神经元通过进行剪枝删除。剪枝后的模型更加稀疏,Encoder输出层的维度也会进一步降低,即实现了CR的动态调整。由于剪枝后的模型精度会有微小损失,其误差变化计算方式如下:

(8)

式中:N′代表所裁剪神经元的数量。

算法 1 基于ℓ2范数的模型结构化剪枝1:训练RCCA-Net深度神经网络模型;2:对于FC层中第t个神经元,计算其所有权重的ℓ2范数之和St=∑Nti=1w2i式中:Nt表示第t个神经元的连接数;3:对以上计算的所有St进行排序;4:根据CR和剪枝比例确定阈值k=CR-CR'CR式中:CR表示当前CR;CR'表示预期CR;5:依据排序结果剪去低于阈值k的神经元,并剪去神经元所对应的连接。

4 系统仿真

4.1 实验数据及设置

本文分别在Saleh-Valenzuela[26]和DeepMIMO[27]信道场景下进行仿真验证。Saleh-Valenzuela是一个超带宽室内多径信号模型,描述了信道在时域、频域和空域的随机衰落特性;而DeepMIMO是一个针对大规模MIMO系统的公共数据集。系统仿真参数设置如表1所示。

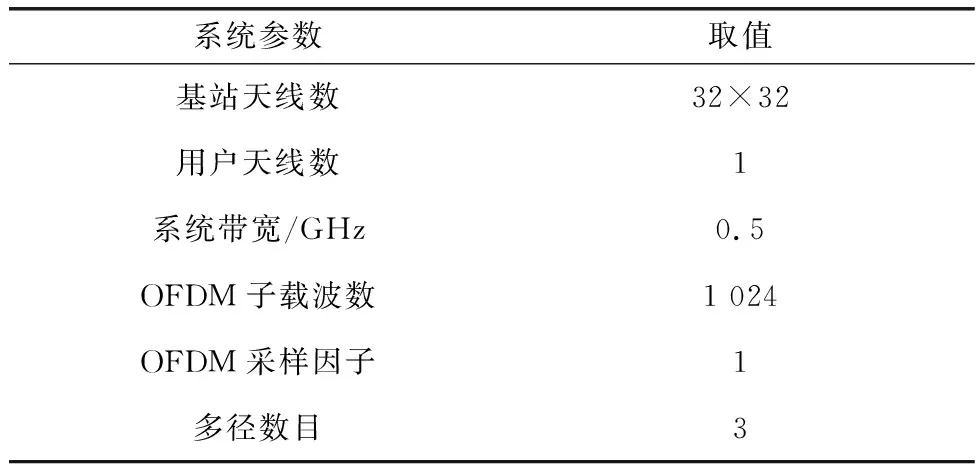
表1 系统参数设置

在模型训练过程中,训练集、验证集和测试集的样本数分别是100 000、30 000和20 000,所有样本值作归一化处理。为了使模型每一层输出方差尽可能相等,使用Xavier初始化器对模型参数进行初始化,使用Adam在训练集上迭代更新模型参数。训练轮数、初始学习率和批次大小分别是1 000、0.001和256。为了避免震荡,使模型能更好地收敛到最优解,设置学习率每经过200轮衰减为原来的50%。使用归一化MSE(normalized MSE,NMSE)描述模型在不同信道场景下的反馈精度,其定义如下:

(9)

4.2 复杂度计算

RCCA-Net编码器主要是由卷积层和FC层组成,定义[Cin,Cout,K]表示输入通道数为Cin、输出通道数为Cout、卷积核大小为K的卷积层;[Nin,Nout]表示输入神经元数为Nin、输出神经元数为Nout的全FC层。NConv、NBN和NFC分别表示卷积层、批归一化层和FC层的浮点运算量(floating-point operations,FLOPs)。这里,将一次乘加(multiply and accumulate)算作两个浮点运算,NConv、NBN和NFC的计算方式如下:

NConv=K2CinCout+Cout

(10)

NBN=4Cout

(11)

NFC=NinNout+Nout

(12)

假定Encoder端双层FC网络的第1层神经元数量为N,第2层(Encoder输出层)神经元数量为M,这个双层全连接网络的计算量为NM+M。对Encoder输出层进行剪枝,将输出层神经元数量由M减少到M′,其计算量也将变为NM′+M′。当M′减小到M的1/2时,Encoder端的参数量和计算量都将减小为原来的1/2。

4.3 RCCA-Net反馈模型分析

本节以CsiNet+信道反馈模型[14]为对比方案,并以基于CS的OMP和AMP重构算法作为基准实验。图5和图6是4种方法分别在Saleh-Valenzuela和DeepMIMO场景下反馈精度的对比情况。由图5和图6可知,基于DL的RCCA-Net和CsiNet+明显优于OMP和AMP算法,而RCCA-Net恢复精度相较于CsiNet+也有所提升。结合图5和图6分析可发现,RCCA-Net在两种场景下对信道矩阵的恢复性能基本稳定,而CsiNet+波动较大,表明本文提出的残差信道特性注意机制有效学习了信道矩阵的内部特性,模型在不同数据集上具有良好的泛化性,能适应实际通信系统中复杂多变的信道条件。

图5 Saleh-Valenzuela信道下NMSE性能Fig.5 NMSE performance under Saleh-Valenzuela

图6 DeepMIMO信道下NMSE性能Fig.6 NMSE performance under DeepMIMO

4.4 动态调整CR性能分析

本节以RCCA-Net在Saleh-Valenzuela和DeepMIMO数据集上得到的模型为基准进行剪枝,以实现CR的动态调整,同时对不同CR下模型的参数量变化、存储空间和反馈精度进行了比较分析。

结合RCCA-Net模型分析可知,当CR=1/4时,FC层的参数量为1 927 748,占模型参数总量2 103 086的90%以上,占用了大部分的内存空间,因此动态调整CR的关键就是通过模型剪枝减少FC层的参数量。表2是剪枝后不同CR下模型参数量变化及在不同场景下的性能比较,RCCA-Net的参数量为2 103 086个,模型大小为8.96 M,在Saleh-Valenzuela和DeepMIMO信道下的反馈误差分别为-17.21 dB和-12.92 dB。当CR调整到1/8,模型的参数量减少了49.87%,而在Saleh-Valenzuela和DeepMIMO上反馈精度只有0.75 dB和2.05 dB的损失,可以看出在剪枝调整CR后,模型依然保持了较佳的反馈性能。即使CR调整到1/32,模型在两数据集上也仅有1.24 dB和3.37 dB的性能损失,而模型大小减少了78.24%,极大地节省了用户设备的存储空间,为模型的实际部署应用提供了可能性。上述分析说明了本文提出的基于2范数模型结构化剪枝动态调整CR方案的可行性及有效性,在满足不同用户端设备及信道条件的场景下保证了CSI反馈的准确性。

表2 剪枝后模型大小和参数变化情况

为了进一步直观说明剪枝前后的恢复效果,将不同CR下恢复的信道矩阵以灰度图像的方式进行可视化展示,如图7所示。选取了不同CR下的5个样本构成5张灰度图像,由于大规模MIMO信道在角度-时延域表现出的稀疏性,大部分元素值接近0,仅包含少量的信息,所以图像大部分区域表现为白色。当CR=1/4时,RCCA-Net的恢复结果几乎不含任何噪声,和原始数据十分接近,这表明RCCA-Net能有效对反馈的信道矩阵进行恢复。随着CR的增大,反馈的信道信息中包含的有效信息逐步减少,更易受噪声干扰,使得重构精度有所下降,但信道矩阵的基本特征仍然可重建恢复,可在频谱资源极度稀缺的场景下使用高CR进行CSI反馈。

图7 不同CR下重建效果可视化Fig.7 Reconstruction performance visualization under different CR

表3是本文提出的RCCA-Prune与SM-CsiNet+[14]在压缩率调整过程中模型大小和参数量的变化。

表3 RCCA-Prune与SM-CsiNet+调整CR方案比较

在CR=1/4时,RCCA-Prune和SM-CsiNet+的参数量和模型大小几乎相同,以CR=1/4作为CR调整基准。随着CR增大,SM-CsiNet+由于级联FC层使得模型复杂度大幅增长,而剪枝后的RCCA-Prune裁剪掉了冗余的参数和神经元,模型大小逐步减少,在高CR下模型更加稀疏。在CR=1/32时,RCCA-Prune模型的大小相较于SM-CsiNet+减少了18.97%,更适合部署在用户设备中;而参数量仅为SM-CsiNet+的10.93%,大幅缩减了模型计算推理时间,可满足不同系统实时反馈的需求,RCCA-Prune在模型大小和参数量方面的优势也为模型的实际部署应用提供了可能性。

图8和图9展示了在不同CR下两种方案重构性能的比较。

图8 Saleh-Valenzuela信道下重建性能Fig.8 Reconstruction performance under Saleh-Valenzuela channel

图9 DeepMIMO信道下重建性能Fig.9 Reconstruction performance under DeepMIMO channel

从图8和图9中可以看出,与级联压缩方案SM-CsiNet+相比,RCCA-Prune在CR调整过程中重构误差更低。当CR=1/4时,在Saleh-Valenzuela 信道和DeepMIMO场景下,两种方案的重构性能相当;但随着CR的增大,RCCA-Prune性能基本保持稳定,在CR=1/32时只有大约2 dB的性能损失,说明本文提出的RCCA机制充分学习了信道统计特征,剪除了冗余的神经元,使模型更加稀疏,而信道特征信息的少量损失可以忽略不计,仍然可以保证通过Decoder对信道信息恢复重建。而SM-CsiNet+的级联压缩方式在高CR下重建性能急剧下降,在CR=1/32时已无法对DeepMIMO信道场景下的CSI进行恢复,这是因为SM-CsiNet+级联FC层破坏了模型结构,导致在高CR下特征信息提取缺失,Decoder可利用的有效信息减少,无法对信道矩阵精准重构。综上,本文所提出的RCCA-Prune可以在保证反馈精度的基础上依据系统需求动态调整CR,参数量和模型大小远远小于SM-CsiNet+,且重构精度更高,是一种高效的CR动态调整方案。

5 结 论

本文提出了一种大规模MIMO FDD系统下基于RCCA机制的CSI反馈模型RCCA-Net和基于2范数模型结构化剪枝动态调整CR的方法RCCA-Prune;RCCA-Net可充分挖掘复信道矩阵实部虚部所形成的两通道间的依赖关系,显著提高CSI重建质量,在保证较高反馈精度的基础上减少了CSI反馈开销。RCCA-Prune是一种灵活高效的动态调整CR方案,以2范数评估各神经元对最终结果的贡献度,依据CR设置、通过模型结构化剪枝删除对应数量的神经元,不需要对模型进行重复训练,弥补了当前基于DL的CSI反馈模型只能以固定压缩率进行反馈的缺点。从仿真结果可知,RCCA-Prune在不同CR下均能保持较佳的反馈性能,在不同信道场景下的测试也显示RCCA-Prune具有良好的泛化性;且剪枝后的模型大小和参数量都更少,非常适合在成本和性能受限的用户设备中部署使用。本文提出的剪枝动态调整CR方案十分灵活,可以推广到其他基于DL的CSI反馈模型中,在CSI反馈量一定的情况下,通过选择合适的CR,使系统性能在实际场景中达到最优。