基于自适应MEDLL的伪卫星室内多径估计算法

夏文清, 王 庆, 张 波, 阳 媛

(东南大学仪器科学与工程学院, 江苏 南京 210096)

0 引 言

在伪卫星室内定位系统中,由于室内独有的复杂环境和大量墙体,多径效应会比室外环境更加严重[1]。又由于阴影效应和远近效应的影响,接收机有时会处于低信噪比环境下。在这种环境下,多径效应不仅仅会导致定位精度下降[2],更有可能导致信号直接失锁,严重影响定位效果。因此,低信噪比环境下的抗多径算法研究对于伪卫星室内定位而言是不可或缺的。

目前已经有大量学者针对全球卫星导航系统进行了用各种方法抗多径的相关研究[3-6]。由于伪卫星系统与全球卫星导航系统信号体制十分相似,因此针对室外卫星定位的抗多径算法也可以用于伪卫星系统中。但是由于室内环境与室外环境区别较大,因此在选用算法时需要针对室内环境进行选择与改进。

1992年,Nee[7]提出了经典的多径估计延迟锁定环路(multipath estimating delay lock loop, MEDLL)算法,该算法基于极大似然估计原理估计多径信号参数,再利用估计值重构多径信号相关函数,并将其从实际相关结果中消除,从而实现直射信号相关结果的复原。文献[8-11]证明,该算法对噪声不敏感,对伪码多径和载波多径都有着很好的抑制作用,很适合应用于伪卫星室内抗多径。但该算法的缺点在于计算量大,要求匹配多个相关器,且需要事先知道多径条数。随着芯片技术的发展,计算量大和多相关器的问题已经逐步得到解决,但该算法对多径条数的要求仍不能完全解决。

目前有一部分MEDLL改进算法对多径条数进行了计算或估计。刘亚欢等[12]采用网格化估计的方法,先假设多条多径信号的时延,再根据求得的幅值来判定多径信号是否存在。虽然在其基础上,唐斌等[13]添加有色噪声卡尔曼滤波器,减小了噪声的影响,但总体而言,这种网格化估计的方法相比基础MEDLL方法增加了对噪声的敏感性,同时时延估计的分辨率也不高;魏国庆等[14]和Hui等[15]将Teager-Kaiser(TK)算子[16]与MEDLL结合,利用TK算子获取多径条数与其粗略时延,再利用MEDLL实现具体参数估计,实测数据[17]证明该算法在室外是有效的。但是,由于TK算子本身对噪声敏感,因此在低信噪比环境下,由于TK算子可能监测出错误的多径条数与时延,该算法表现不是很好。

事实上,目前绝大多数的多径估计算法,如卡尔曼滤波及其改进算法[18-20]、粒子滤波算法[21-23]等,都没有涉及到多径条数的估计。在多径条数的确定方法上,有的文章直接假定多径信号只有一条[24-25],有的文章只在模型中设定了多径条数,但没有求解[26-28]。这些方式在室外也许可行[29],但是在室内环境中,由于环境复杂且墙体众多,所以多径条数很可能不止一条。在这种情况下,就必须进行多径条数的估计,而现有的多径条数估计方法都对噪声比较敏感,在室内低信噪比环境下表现不好。因此,要想将MEDLL算法应用于伪卫星室内定位,就需要提出一种新的在低信噪比条件下表现良好的多径条数估计方法。

针对这一问题,本文提出一种基于自适应MEDLL的多径估计算法。相比传统MEDLL算法,该算法增加了一个参考相关器,用参考相关器相关值的标准差作为衡量标准,与其他相关器经过MEDLL算法消除所有信号后的噪声相关值的标准差进行比较,进而得到多径条数。该算法能在信噪比较低的状态下正确估计多径信号条数,更适合应用于伪卫星室内定位系统抗多径。

1 多径信号模型

伪卫星系统在进行定位时,其接收机接收到的中频信号通常可以表示为

(1)

式中:si(t)表示第i路信号;αi,τi,φi表示第i路信号的幅度、相对本地C/A码的时延、相对本地载波的相位;c(t)表示C/A码(忽略导航电文);n(t)代表环境噪声;i=0代表直射信号;M代表多径信号条数;ωIF代表中频频率。

中频信号首先与本地载波进行相乘混频,经低通滤波器滤除高频成分,然后与本地C/A码进行相关运算。设相关器的延迟为τ,则相关函数为

(2)

式中:R(τ)代表C/A码自相关函数;n′(τ)为环境噪声经过混频滤波后与本地信号进行互相关得到的结果。

自适应MEDLL算法基于极大似然估计的原理,用相关结果Rx(τ)估计出各多径信号的多径参数αi、τi、φi,进而对其进行消除。

2 自适应MEDLL算法

2.1 自适应MEDLL算法流程

为了对多径信号条数进行估计,本算法的信号处理模块相比MEDLL算法增加了一对参考相关器(Iref,Qref)。用多径条数估计策略将其输出Rref(t)与多径参数估计结果进行对比,从而得到多径条数的估计。该算法的具体结构如图1所示。

图1 自适应MEDLL算法结构(相关器部分)Fig.1 Algorithm structure of adaptive MEDLL (correlator part)

2.2 多径参数估计

2.2.1 参数估计流程

自适应MEDLL与传统MEDLL算法的多径参数估计方法类似,其流程如图2所示。

图2 MEDLL多径参数估计流程Fig.2 MEDLL multipath parameter estimate flowchart

在多径条数M已知的情况下,自适应MEDLL算法与传统MEDLL算法都采用从第一路信号开始、信号条数不断增加、依次循环优化的方法进行多径参数估计[30]。这种方法虽然比较消耗算力,但估计精度高且性能稳定。

假定多径条数为M,在多径估计时,该方法首先估计直射信号参数,然后针对两路信号进行循环优化,之后是三路信号的循环优化,以此类推,直至完成M+1路信号(M路多径信号和一路直射信号)的循环优化。其具体计算流程如算法1所示。

算法 1 MEDLL多径参数估计流程1 获取实测相关结果Rx(τ)2 将实测相关结果Rx(τ)作为直射信号s0(t)的相关函数的估计R^0(τ)=Rx(τ)3 根据R^0(τ)估计出s0(t)的参数φ^0、τ^0、α^04 生成s0(t)的重建相关函数R'0(τ)5 For 信号条数m={2,3,…,M+1}6 While 参数估计结果有变化7 For 当前信号j={m,0,1,2,…,m-1}8 计算当前信号sj(t)的相关函数估计9 R^j(τ)=Rx(τ)-∑mi=0,i≠jR'i(τ)10 根据R^j(τ)估计sj(t)的参数φ^j、τ^j、α^j11 生成sj(t)的重建相关函数R'j(τ)12 End for13 End while14 End for15 估计完成

2.2.2 参数估计方法

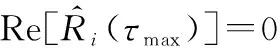
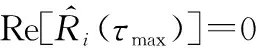
进行时延估计采用的是鉴相函数法,即选取某个采样点作为即时码相关点,选定码间距后进行鉴相,根据鉴相结果得到实际时延与即时码相关点之差,进而得到实际时延。

早晚码相干鉴相器容易受到噪声干扰,是因为它只使用了两路相关结果,而MEDLL算法本身就是一种多相关器算法,所以采用多相关鉴相器(如strobe鉴相器)不仅不会带来额外的算力需求,还能得到更准确、稳定的鉴相结果[31]。因此,本文提出用strobe相关器进行时延估计,具体步骤如下:

步骤 1在开始信号处理前,事先计算好strobe鉴相器的鉴相函数e=D(ε)及其反函数ε=D-1(e)。

步骤 2选取采样点τx。为减少噪声和多径影响,并且尽量保证鉴相实际函数单调,该点应当选取功率最大点τmax。

(4) 相关函数重建

2.2.3 多径条数估计策略

图3 多径条数估计策略流程Fig.3 Strategy flowchart of multipath number estimation

步骤 2取一段时间内的参考相关器值Rref(t),对其同样求标准差,得到参考值σref。

步骤 3比较σM-1、σM与σref,若σM-1<σref,或σM>σref,则使对应的计数器增加,其他计数器减少。

步骤 4若σM-1对应的计数器大于门限值(手动设定),则多径条数估计值变为M-1。同理,若σM对应的计数器大于门限值,则多径条数估计值变为M+1。

在多径条数为2时,σref与σM-1、σM随时间变化的结果如图4所示。

图4 多径条数估计过程Fig.4 Process of multipath number estimation

从图4可以看出,随着时间推移,多径条数估计值M从初始值0增加为2,并且稳定下来,这说明多径条数估计策略是有效的。

3 实验结果与分析

3.1 多径估计性能测试

为测试自适应MEDLL算法在各种噪声环境与多径条件下的多径估计效果,本文采用Matlab仿真平台进行了多项实验。实验采用GPS L1 PRN1信号。设定普通相关器时延从-1码片到1码片,间隔0.05码片,共41个普通相关器。参考相关器时延为2码片。设定直射信号时延为0码片,幅值为1 mV;设定多径条数为1,其幅值为0.5 mV,时延为0.5码片。

保持多径信号幅值维持在0.5 mV不变,改变其时延,时延估计结果的误差均方根随时延实际值的变化在不同噪声环境下的结果如图5所示。

图5 时延估计误差随时延实际值的变化Fig.5 Delay estimation error varies with delay actual value

由图5可以看出,自适应MEDLL算法在对时延较小(小于0.1码片)的多径信号进行估计时效果较差。在信噪比较高的环境下,这一趋势虽然不明显,但在低信噪比环境下估计误差会突增,这是由于算法误将短时延多径信号与直射信号识别为同一信号的缘故。在时延估计误差急剧增大(即信噪比为-25 dB)、时延为0.1码片的情况下,截取35 ms的多径参数估计结果如图6所示。

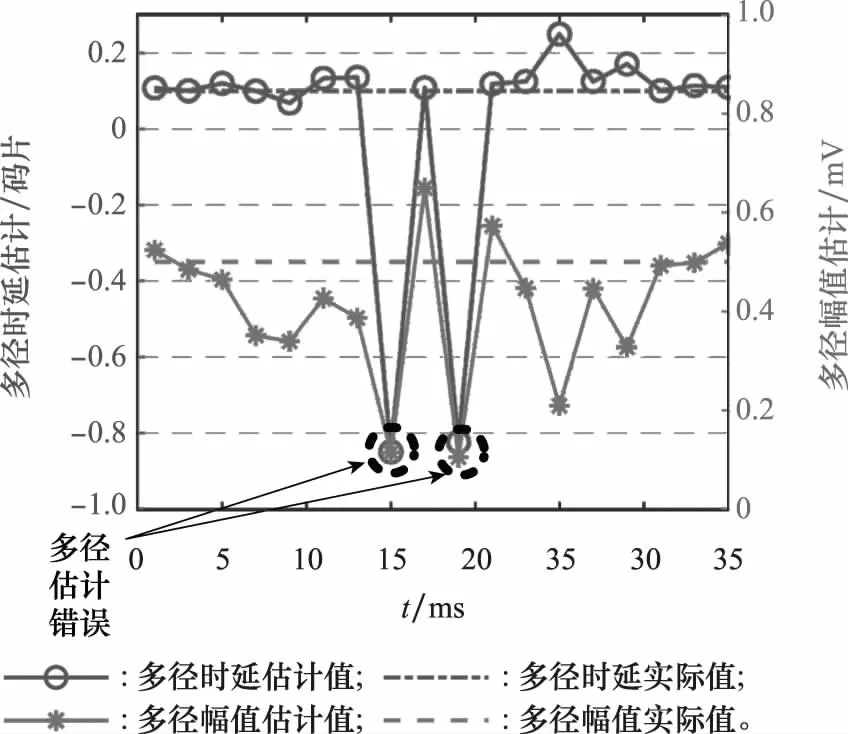
图6 短时延多径信号估计误差Fig.6 Short-delay multipath signal estimation error

由图6可以看到,估计结果大部分时间是正确的,但在15 ms、19 ms、24 ms时,时延估计极度偏离实际值,且幅值估计接近于0 mV,这一结果证明此时算法将短时延多径信号与直射信号混淆,并将噪声识别为多径信号。这一错误发生频率不高,可以通过其他方法(如滤波或检测)解决。

通过突变检测的方法将估计错误的数据剔除后,重新计算时延估计结果的误差均方根随时延实际值的变化在不同噪声环境下的结果如图7所示。

图7 修正后时延估计误差随时延实际值的变化情况Fig.7 Delay estimation error after correction varies with delay actual value

从图7可以看出,在不发生错误的情况下,自适应MEDLL算法的时延估计误差在同一信噪比下比较稳定。

类似地,保持多径信号时延维持在0.5码片不变,改变其幅值,幅值估计结果的误差均方根随幅值实际值的变化在不同噪声环境下的结果如图8所示。

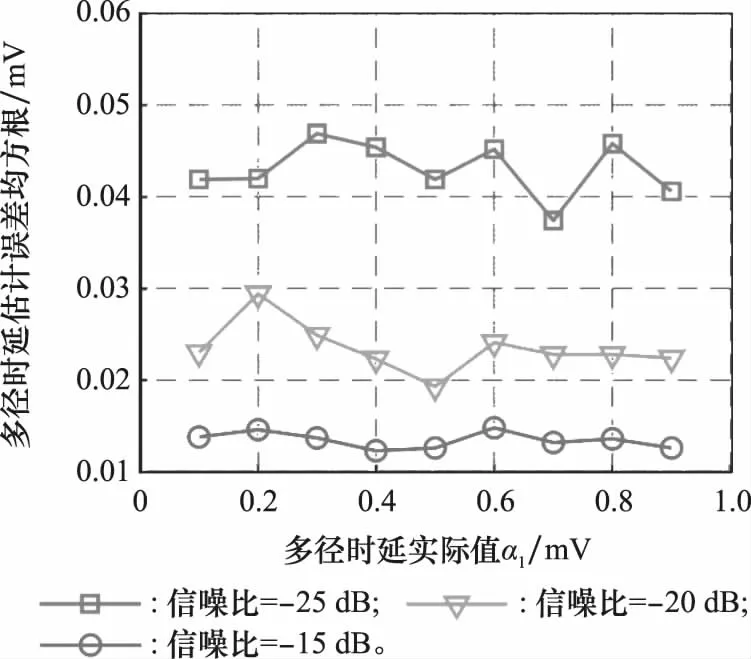
图8 幅值估计误差随幅值实际值的变化情况Fig.8 Amplitude estimation error varies with amplitude actual value

由实验结果可以看出,自适应MEDLL算法对不同幅值多径的适应性较好。即使在低信噪比环境下,对不同幅值多径的估计效果也没有太大变化。

3.2 定位性能测试

为测试自适应MEDLL算法的实际定位效果,本文采用Matlab仿真平台进行了仿真定位实验。实验采用GPS L1 PRN1信号。设定普通相关器时延从-1码片到1码片,间隔0.05码片,共41个普通相关器。参考相关器时延为2码片。实验假定的室内环境多径情况复杂且多变,因此设定多径信号的条数在1～3之间变化,且多径时延、相位和幅值在一定范围内随机取值。

实验结果中,采用和未采用自适应MEDLL算法的即时码相关结果如图9所示。

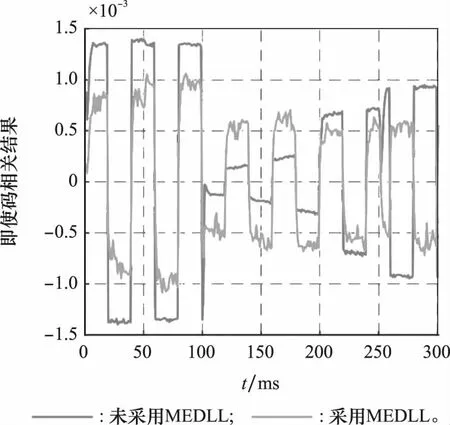
图9 即时码相关结果对比Fig.9 Comparison of prompt code correlation result

从图9可以看到,由于多径信号的影响,未采用自适应MEDLL算法时,即时码的相关结果绝对值变化幅度较大,尤其是当相关结果的绝对值较小时,很可能会产生导航电文误码,这对实际定位非常不利。而在采用自适应MEDLL算法后,多径信号对即时码相关结果的影响明显减小,证明自适应MEDLL算法在接收机定位时有抗多径效果。

3.3 对比实验

为了对比在低信噪比下自适应MEDLL算法与其他MEDLL改进算法的性能,本实验将采用本算法得到的多径估计结果与TK-MEDLL算法和网格化MEDLL算法得到的多径估计结果进行分析。实验在Matlab仿真平台上进行。为了确保试验的严谨性,算法参数保持一致:实验采用GPS L1 PRN1信号。设定普通相关器时延从-1码片到1码片,间隔0.05码片,共41个普通相关器。参考相关器时延为2码片,网格化MEDLL算法估计范围从0到1码片,间隔0.05码片。各路信号参数为时延τ=[0,0.2,0.5]码片,幅值α=[1,0.5,0.5]mV。

实验结果中,3种算法的多径条数估计结果如图10所示。

图10 多径条数估计结果对比Fig.10 Comparison of multipath number estimation result

由图10可以看出,TK-MEDLL算法和网格化MEDLL算法的多径条数估计结果错误较多。对于TK-MEDLL算法而言,这是由于TK算子容易受噪声影响,因此多径条数估计值波动较大,频繁发生错误;对于网格化MEDLL算法而言,这是因为该算法用多径幅值估计的结果作为多径条数估计的依据,而多径幅值估计结果受噪声影响误差较大,所以导致多径条数估计不准。相比之下,自适应MEDLL算法在过渡期结束后的多径条数估计结果一直保持稳定,为后续进行准确的多径参数估计提供了保障。

实验结果中,3种算法的直射信号幅值估计结果如图11所示。

图11 直射信号幅值估计结果对比Fig.11 Direct signal amplitude estimation result comparison

从图11可以看出,相比于网格化MEDLL算法和TK-MEDLL算法,自适应MEDLL算法的直射信号幅值估计结果波动更小,其误差均方根为0.055 mV。作为对比,TK-MEDLL算法的直射信号幅值估计误差均方根为0.097 mV,网格化MEDLL算法的直射信号幅值估计误差均方根为0.135 mV。这证明在低信噪比条件下,自适应MEDLL算法的多径估计结果更加准确。

改变信噪比,进行多次重复实验,3种算法的直射信号幅值估计误差均方根随信噪比的变化情况如图12所示。

图12 直射信号幅值估计误差均方根对比Fig.12 Comparison of direct signal amplitude estimation error root mean square

由图12可以看出,在信噪比高时,3种算法的性能并没有明显区别,而随着信噪比降低,自适应MEDLL算法的多径估计误差提升更慢。相比网格化MEDLL算法,自适应MEDLL算法的直射信号幅值估计误差均方根最高可以降低59%,相比TK-MEDLL算法最高可以降低43%,这说明这一算法对噪声更不敏感,在低信噪比条件下有着更好的性能。

4 结 论

针对室内环境下伪卫星定位系统受多径效应影响严重的问题,本文提出了一种基于自适应MEDLL的伪卫星室内多径估计算法。该算法在MEDLL的基础上增加了一个参考相关器,以该相关器输出值为衡量基准,对其余相关器经过MEDLL消除所有信号影响后的噪声相关值进行比较,从而得到多径条数的准确估计。性能测试实验表明:① 自适应MEDLL算法对不同时延、不同幅值多径的适应性都较好,虽然在低信噪比环境下对低时延多径信号会存在误判,但用简单的检测或滤波就可以进行修复;② 在低信噪比环境下,网格化MEDLL算法和TK-MEDLL算法均不能正确估计多径条数,而自适应MEDLL算法仍能进行正确的估计,进而保障多径参数估计的准确度;③ 随着信噪比降低,自适应MEDLL算法的多径估计误差提升更慢。相比网格化MEDLL算法,自适应MEDLL算法的直射信号幅值估计误差均方根最高可以降低59%,相比TK-MEDLL算法最高可以降低43%,这说明这一算法对噪声更不敏感,在低信噪比条件下有着更好的性能,更加适用于伪卫星室内定位系统抗多径。

此外,虽然本文提出的多径条数估计策略与MEDLL算法配合得更为紧密,但此多径条数估计策略并不仅仅适用于MEDLL算法。在卡尔曼滤波等其他抗多径算法中,也可以将其添加进去,除了会增加一些算力消耗,并不会引起冲突。可以预见,该多径条数估计策略可以在各种多径估计算法中发挥自身的作用。