序列ISAR像复杂结构航天器在轨姿态估计

寇 鹏, 刘永祥, 张 弛, 李玮杰, 张双辉, 霍 凯

(1. 国防科技大学电子科学学院, 湖南 长沙 410073; 2. 西安卫星测控中心, 陕西 西安 710600)

0 引 言

航天器姿态是描述其在轨状态的主要参数,更是判断其动作意图以及故障抢救的重要依据。航天器姿态通常定义为轨道坐标系下的偏航角、俯仰角和滚动角。一般而言,大部分正常工作的航天器为三轴或自旋稳定姿态,而失效的航天器多为重力梯度稳定或自由翻滚等姿态[1-3]。逆合成孔径雷达(inverse synthetic aperture radar, ISAR)具有全天时、全天候工作的优点,是航天器姿态估计的重要手段[4-6]。

航天器ISAR像可以看作是其三维结构在成像平面上的投影。ISAR成像不同于光学成像,其成像平面与雷达视线(line of sight, LOS)和目标位置紧密相关。文献[7-8]认为成像平面为相干积累时间(coherent processing interval, CPI)内LOS扫过的平面,这种假设忽略了LOS通常为非共面矢量,因而其仅适用于雷达站在航天器轨道面内或CPI非常短的特殊情况。通常而言,姿态稳定航天器为了提高方位向的分辨率,往往需要较长CPI,LOS的非共面性一般不能忽略。目前,航天器姿态估计的方法主要有两种。第一种是基于三维重建的方法[9-12],这种方法通过散射点相关性的因子分解方法重构目标的几何结构,从而估计目标的姿态。这种方法本质是获得不同姿态下散射中心的投影矩阵关联,缺点是对视角变化较为敏感,容易受“角闪烁”和噪声等影响。第二种是典型结构模板匹配法[13-15],这种方法通常需要提取特定的几何结构(如矩形、线性结构等)进行匹配,在观测积累数据样本充分的情况下,这种方法具有较高的估计精度[16-17]。但现有方法对几何结构的提取常需要人工介入[18-19],且对复杂结构航天器姿态估计的最优几何结构选取问题,目前尚未见到相关文献报道。

本文提出了对成像CPI内LOS矢量进行奇异值分解(singular value decomposition, SVD)[20],从而得到最优ISAR成像平面的方法。在此基础上,提出了利用Unet3+深度网络[21]分割出航天器典型部件,进而自动提取典型部件的线性结构的方法。针对实测ISAR像存在散焦、腔体散射和噪声等造成部件尺寸提取误差较大的问题,提出了使用不同部件结构建立优化函数,通过求解不同结构的优化函数从而得到复杂结构航天器在轨姿态角的方法。

1 在轨姿态稳定航天器ISAR成像平面分析

1.1 在轨航天器坐标系与姿态角定义

如图1所示,建立J2000.0惯性坐标系O-XeYeZe,坐标原点为地球质心O,Xe轴在基本平面内由地球质心指向J2000.0惯性坐标系的平春分点,Ze指向北极方向,Ye轴与Xe轴、Ze轴构成右手坐标系。建立轨道坐标系Ot-XoYoZo,坐标原点为航天器质心Ot,Xo轴指向航天器运动方向,Yo轴指向轨道面的负法向,Zo轴指向地心。建立本体坐标系Ot-XsYsZs,坐标原点为航天器质心Ot,Xs轴指向航天器主体最长轴方向;Ys轴指向航天器帆板方向,Zo轴与Xs轴、Ys轴构成右手系。

图1 在轨航天器坐标系Fig.1 In orbit spacecraft coordinate system

如图2所示,航天器在轨姿态定义为本体坐标系与轨道坐标系的夹角,即偏航角α、俯仰角β和滚动角γ。姿态角可以理解为轨道坐标系按Z-Y-X顺序旋转α、β和γ到本体坐标系。一般而言,姿态稳定航天器的α、β和γ保持不变。

图2 在轨航天器姿态角定义Fig.2 Definition of attitude angle of spacecraft in orbit

1.2 姿态稳定航天器ISAR等效成像平面

如图3所示,当雷达站不在航天器轨道面内时,在一个CPI内,各时刻雷达LOS不在同一平面内,通常不能简单地认为雷达LOS扫过的即为成像平面,因此这里提出通过SVD分解寻找最优等效成像平面的方法。

图3 姿态稳定航天器ISAR等效成像平面Fig.3 ISAR equivalent imaging plane of attitude stabilized spacecraft

若ti(i=0,1,…,N)时刻,雷达在J2000.0惯性坐标系下位置矢量为ORti,航天器在J2000.0惯性坐标系下位置矢量为OTti,则雷达LOS矢量RTti为

RTti=ORti-OTti

(1)

定义CPI内LOS矢量矩阵LOST为

LOST=[RTt0,RTt1,…,RTtN][RTt0,RTt1,…,RTtN]T

(2)

利用SVD分解将LOST进行分解:

LOST=UΔVT

(3)

式中:Δ∈R3×3为对角矩阵,其对角元素为LOST的奇异值;U∈R3×3、V∈R3×3均为列正交矩阵。记Δ最小奇异值对应的行号为minl,U的第minl行向量为umin l,则等效成像平面的距离向矢量aR可以表示为

(4)

等效成像平面的距离向矢量aC可表示为

aC=aR×umin l

(5)

等效成像平面的法向量aL可以表示为

aL=aC×aR

(6)

2 航天器部件分割与线性结构提取

2.1 基于Unet3+神经网络的航天器部件分割

Unet3+中的每一个解码器都结合了全部编码器的特征,这些不同尺度的特征能够获取细粒度的细节和粗粒度的语义,能有效弥补Unet[22]和Unet++[23-24]不能精确分割图像中部件位置和边界的缺点,因此本文采用Unet3+网络进行部件分割,网络结构如图4所示[21]。网络损失函数采用Focal LOSS[25]与IOU(intersection over union)LOSS[26]的加权求和,其中Focal LOSS主要是为了解决目标检测中正负样本比例严重失衡的问题。IOU损失表示预测框A和真实框B之间交并比的差值,反映预测框的检测效果。

图4 Unet3+网络模型Fig.4 Unet3+network model

2.2 部件线性结构提取

3 在轨航天器ISAR成像投影关系与姿态求解

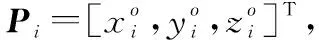
(7)

(8)

若航天器等效线性结构矢量为

M=Pi-Pj(i≠k)

则M的ISAR像TM为

(9)

可见TM中不包含图像中心[u0,v0]T,即消除了序列ISAR图像中心偏移对姿态估计的偏差。利用三维姿态在成像平面的投影误差建立优化函数,通过经典粒子群优化(particle swarm optimization, PSO)算法[28]等优化方法可以最终实现在轨姿态的优化求解估计。若航天器第j个部件的线性结构矢量为Μj=[m1j,m2j,m3j],Mj在tj时刻的成像平面投影可以写为

(10)

若总观测时长tN时间内共得到N幅ISAR像,姿态估计问题可以转化为求解代价函数f(α,β,γ)的最小值:

(11)

利用PSO即可求解该优化函数。事实上,图5为德国TIRA雷达公布的实测航天器ISAR像[29]。由于存在散焦、腔体散射和噪声等因素的影响,航天器ISAR像边界轮廓往往确定困难,进而提取的部件尺寸LRj和LCj往往误差较大,而部件在ISAR图像中的矢量方向φj不受图像边界轮廓影响,因此实测序列ISAR图像可采用部件线性结构矢量或仅使用矢量方向来估计姿态。

图5 德国TIRA雷达实测航天器ISAR像Fig.5 ISAR images of spacecraft measured by Germany TIRA radar

4 本文算法流程

本文算法流程如图6所示。首先根据雷达回波数据,采用传统RD算法进行ISAR序列成像;然后对得到的ISAR图像序列进行部件分割和线性结构提取,获取其在RD成像平面内的长度、方向等观测信息;接着通过航天器轨道及雷达站位置信息计算各帧图像对应的成像平面,利用成像投影几何关系进行图像线性结构的提取匹配估计姿态角。

图6 本文算法流程图Fig.6 Flowchart of the proposed algorithm

5 仿真实验

在仿真实验中,设置雷达站址为北纬107.616°,东经33.126°,高程为10 m。雷达中心频率为10 GHz,带宽为1 GHz,脉冲重复频率为100 Hz,脉宽为5 μs。第5.1节验证了本文所提等效成像平面的准确性;第5.2节分析了不同轨道航天器ISAR成像CPI时间内LOS非共面性;第5.3节分析了不同线性结构对航天器在轨姿态估计误差的影响。

5.1 航天器ISAR等效成像平面准确性验证

图7为利用42个点模型模拟包含圆柱主体和太阳能帆板的航天器。航天器轨道高度为375 km,倾角为43.012°,绕地周期为92.193 min,仿真时长为500 s。首先,根据雷达站对点模型回波进行仿真,利用距离多普勒(range Doppler, RD)算法得到序列ISAR图像,典型结果如图8(a)和图8(d)所示。图8(a)中CPI内LOS在轨道坐标系内的变化曲线如图9所示,可见一般情况下LOS为非共面矢量。图8(b)和图8(e)使用Otsu算法[30-31]提取序列ISAR图像的散射点位置。根据推导的等效成像平面在J2000.0惯性坐标系中的位置,将目标的三维坐标投影到成像平面上,得到序列“投影图像”如图8(c)和图8(f)所示。最后,逐点比较序列ISAR图像散射点和三维点模型在不同成像平面“投影图像”的位置误差,验证本文所推导的等效成像平面的准确性。

图7 点模型三维分布Fig.7 Three-dimensional distribution of point model

图8 点模型的ISAR像、散射中心及投影像Fig.8 ISAR image, scattering center and projection image of point model

如图8(c)、图8(f)所示,以CPI起止帧LOS构成的成像平面与图8(b)、图8(e)所示散射中心逐点匹配后,求得平均欧式距离的位置误差分别为26.5 cm和10.4 cm,而本文提出的等效成像平面平均欧式距离的位置误差分别为7.7 cm和3.6 cm,说明本文提出的等效成像平面更加准确、合理。

5.2 ISAR成像CPI时间内LOS非共面性分析

实验首先分析了在相同CPI时间内,LOS非共面性;然后采用点模型验证ISAR等效成像平面的准确性。选取近圆形轨道高度分别为300 km、500 km和700 km,轨道倾角为55°、98°和120°的共9颗航天器进行分析,利用STK(sa-tellite tool kit)仿真软件及SGP4(simplified general perturbation 4)模型计算航天器位置,利用雷达站的经纬度和高度计算LOS序列。成像CPI定义为成像累积时间取方位像分辨率与距离像分辨率相等的时间。在第1.2节图3中,以本文SVD分解法构成成像平面A,以RTt0和RTtN构成平面B,表1给出了246圈次的平面A与平面B法向量夹角的平均值。

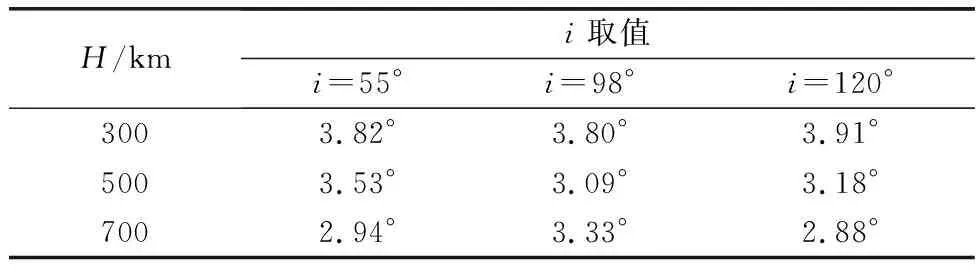
表1 平面A与平面B法向量夹角的平均值

从北京时间2021年5月2日4时0分0秒至2021年5月5日4时0分0秒,雷达对9颗航天器共可见246圈。图10给出了不同轨道参数的平面A与平面B法向量的最大夹角,可见圈次雷达最大俯仰角变化情况,可见CPI时间内LOS是非共面角度,随轨道高度降低而增加,且与雷达最高俯仰角基本是二次抛物线关系。

图10 不同轨道参数平面A与平面B法向量的最大夹角Fig.10 Maximum angle between normal vectors of plane A and B with different orbital parameters

5.3 线性结构选取对“中国空间站”姿态估计精度影响分析

如图11所示,截至2021年6月19日,中国空间站在轨模型为“王”字形结构,模型可以简化成主体、帆板1、帆板2和帆板3四个线性结构。实验首先使用3dmax软件建立中国空间站三维模型,根据中国空间站TLE(two-line element)根数计算航天器在J2000.0惯性坐标系下的位置和速度,然后用物理光学方法计算模型雷达散射截面(radar cross section, RCS),进而仿真雷达回波数据。根据雷达回波,利用RD算法成像后得到序列ISAR像,典型ISAR像结果如图12(a)、图12(g)和图12(m)所示。实验仿真了5个圈次共163幅ISAR像,选取4个圈次共117幅ISAR像作为训练集,选取一个圈次共46幅ISAR像作为测试集。

(1) 部件分割与线性结构提取实验

部件分割典型结果如图12(b)～图12(e)、图12(h)～图12(k)和图12(n)～图12(q)所示,同时利用Radon变换检测的直线与部件分割结果轮廓最远交点可以计算部件的ISAR图像尺寸,根据径向尺寸与横向尺寸比值可以计算得到ISAR图像的部件方向,计算结果如表2所示。整个测试集部件的径向尺寸、横向尺寸和线性结构方向误差如表3所示,可见部件线性结构的尺寸误差相对较大,而线性结构方向尺寸误差相对较小。这其中的原因主要是ISAR图像边缘轮廓较难确定,且散焦、高旁瓣和斑点噪声等因素造成尺寸估计误差较大,而多数散射点相对位置关系分布则较为稳定,所以部件线性结构的方向误差相对较小。

表2 中国空间站典型ISAR像部件尺寸与方向

表3 测试圈部件线性结构矢量平均误差

(2) 不同线性结构姿态估计误差实验

实验对测试圈次46幅ISAR像,分别选取“天和核心舱”的“十”字型、“天和天舟”组合体的“士”字型和“天和天舟神舟十二”组合体的“王”字型3种线性结构组合,不同线性结构矢量对姿态估计的精度如图13所示。

图13 3种线性结构矢量姿态估计误差曲线Fig.13 Error curves of three kinds of linear structure vector attitude estimation

定义平均姿态角误差φ=(α+β+γ)/3,当ISAR像数量为5幅、25幅和45幅时,φ的取值见表4所示。当ISAR像的数量相同时,“王”字形的φ均值最小,“十”字形的φ均值最大,说明在估计复杂结构航天器姿态角时,应该充分选取尽量多的线性结构以减小估计误差。同时,随着使用ISAR像数量增多,φ减小,当ISAR像为45幅时,3种线性结构矢量的平均姿态角误差φ基本相同,均在1°以内。

表4 3种线性结构矢量的平均姿态角误差φ

实测ISAR像部件线性结构矢量尺寸提取往往存在较大误差,但部件线性结构矢量方向通常误差较小,因此仅使用3种线性结构的方向来估计姿态。当ISAR像数量为5幅、15幅和45幅时,仅使用3种线性结构方向的平均姿态角误差φ如表5所示。如图14所示,当ISAR像的数量多于15幅时,3种结构的姿态估计误差几乎相等。同时,当ISAR像数量增多至45幅时,平均姿态角φ误差同样可以小于2°。实验说明在ISAR像数量较多时,仅使用线性结构矢量的方向估计姿态仍然具有较高的精度。

表5 3种线性结构方向的平均姿态角误差φ

图14 3种线性结构方向姿态估计误差曲线Fig.14 Error curves of orientation and attitude estimation of three linear structures

6 结 论

本文从ISAR成像原理出发,分析航天器轨道参数与ISAR成像平面之间的联系,通过雷达LOS矢量SVD分解得到姿态稳定航天器的等效ISAR成像平面。然后,通过深度神经网络及图像处理方法自动获取复杂结构航天器线性部件线性结构矢量。最后,分析了不同线性结构对姿态估计误差的影响。实验表明,等效线性结构越多,姿态估计误差越小;使用的ISAR图像数量越多,姿态估计误差越小。同时,仅采用部件线性结构的方向可有效弥补实测ISAR像中部件尺寸估计误差较大的缺点,进而提升了方法的鲁棒性。