基于GPU的天线组阵信号时延补偿方法

毛飞龙, 焦义文, 马 宏,*, 韩久江, 高泽夫, 李 超, 李 冬

(1. 航天工程大学电子与光学工程系, 北京 101400; 2. 国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

随着航天技术与深空探测技术的迅猛发展,各国对空间的探测向着更深、更远的范围拓展。探测距离将从目前月球探测的40×104km拓展到火星探测的4×108km,以及木星探测的10×108km,这将带来严重的传输损耗,进而导致单天线接收信噪比(signal to noise ratio, SNR)越来越低。天线组阵[1]信号合成是解决单天线接收SNR低的一种重要方法,是指用多个天线构成天线阵列对同一信源的信号进行接收,之后对不同天线接收到的信号进行相干合成,达到提高接收信噪比的目的。天线组阵合成技术的本质是在消除不同天线信号间时延差和相位差后进行相干相加,由于各天线间的噪声(例如大气衰减、雨衰)是随机不相关的,理论上使用N个天线构成的阵列合成信号的SNR是单天线接收信号的N倍[2]。

每个天线接收到的航天器信号存在由空间几何路径、大气传输介质和设备链路造成的时延差异。由空间几何路径产生的几何时延和由大气传输介质产生的传播时延可以根据先验知识进行标校[3]。设备链路是变频系统,会产生设备时延和相位,需要通过设备链路标校技术进行标校。受大气湍流和设备温漂等因素影响,采用上述方法标校后的残余时延和相位仍然存在较大的波动[4],因此信号合成系统还需要以自适应的方式,通过相关处理来估计并实时修正残余时延和相位。

天线组阵合成系统是一个数据密集且高度并行、逻辑复杂、对实时性要求高的系统。随着大规模天线组阵合成系统的天线数量越来越多、接收信号的带宽越来越大,使用单独的图形处理器(graphic processing unit, GPU)已不能满足运算要求。因此,需要寻求能够进行大规模数据运算以及高效并行的体系架构和硬件平台。

近年来,随着高性能计算的发展,GPU从专用于图像领域的处理器逐渐向通用并行计算平台转变。GPU已发展成为一种高度并行化、多线程、多核的通用计算设备,具有杰出的计算能力和极高的存储器带宽,并被越来越多地应用于图形处理之外的计算领域。GPU的运算核心数远多于CPU,更适合于数据密集型计算的并行加速处理。NVIDIA于2007年推出了计算统一设备架构(compute unified device architecture, CUDA),简化了GPU系统的开发流程,使得GPU通用计算技术在信号处理领域得到了更为广泛的应用。目前,基于GPU的信号处理系统具有强大的并行处理能力,能够在短时间内通过并行处理完成大量数据的运算,在GPU资源得到充分利用时,可以实现对信号的实时处理。

因此,基于GPU的信号处理技术成为众多领域的热点,如射电天文[5-6]、雷达[7-8]、无线通信[9-10]、人工智能[11-12]等。本文主要研究天线组阵信号时延补偿方法在GPU平台下的实现与并行优化。

1 天线组阵信号时延补偿方法研究

1.1 天线组阵技术概括

天线组阵技术经过几十年的发展,逐渐形成了五种合成方案[13]:全频谱合成(full-spectrum combining, FSC)、基带合成(baseband combining, BC)、符号流合成(symbol-stream combining, SSC)、载波组阵合成(carrier arraying combining, CAC)、复符号合成(complex-symbol combining, CSC)。除FSC方法,上述方案都属于基于载波跟踪技术的合成方法,需要在阵元载波锁定后合成,不适用于当前大规模的深空天线组阵信号合成系统。

在天线组阵信号合成系统中,由于天线间下行链路的差异性,不同天线接收到同一信源的信号存在时延差,进而导致合成的信号SNR达不到最低解调门限。为了保证能够正确接收和解调信源的信号,就需要在合成信号之前对时延差进行补偿。根据时延差和系统采样率的关系,时延补偿可分为整数时延补偿和小数时延补偿。天线组阵中最常用的合成方法就是全频谱合成,该方法直接在中频进行合成,通过相位差估计[14]算法进行自适应时延与相位的估计并进行补偿。图1所示为天线组阵信号全频谱合成示意图[15]。

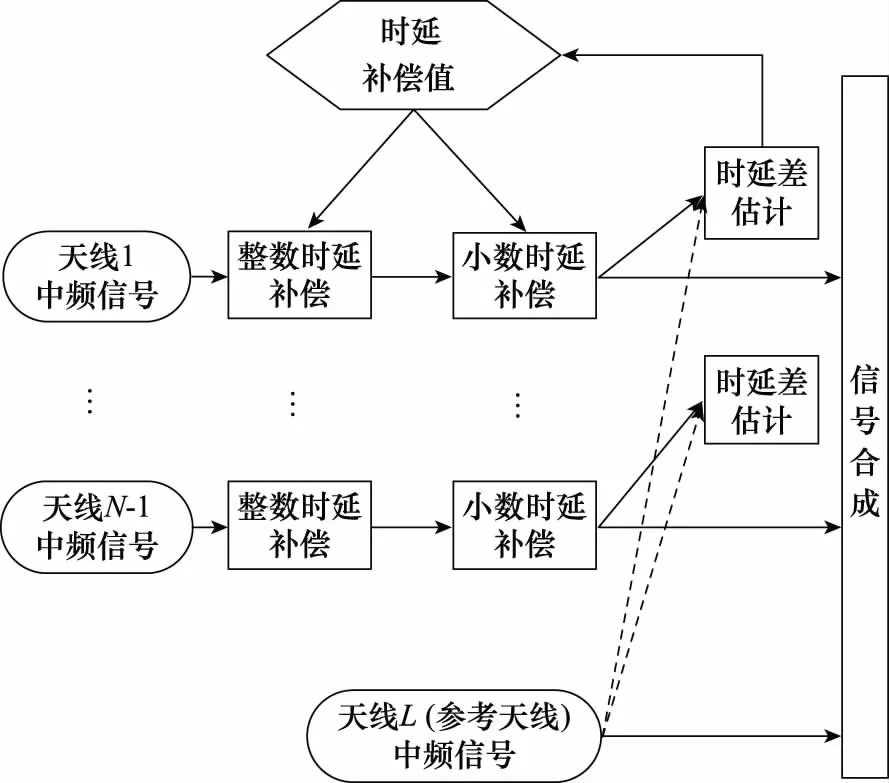
图1 天线组阵信号FSC示意图Fig.1 Schematic diagram of FSC of antenna array signals

为便于分析,假设天线信号为正弦信号。天线1为参考天线,天线2为待修正天线。天线1与天线2接收到的信号为

(1)

(2)

理想情况下,θ21=θ2(t)-θ1(t),即θ21为两天线间的相位差值。之后利用ejθ21对天线2进行补偿:

s2(t)C=Asin[ωct+θ2(t)]·ejθ21

(3)

此时,两天线的相位已对齐,将s1(t)与s2(t)C相干相加可得

s(t)=Asin[ωct+θ1(t)]+Asin[ωct+θ2(t)]·ejθ21

(4)

理论上来说,合成的信号s(t)的SNR为s1(t)的2倍,但实际传输信道中存在着各种噪声干扰,使得合成信号的SNR小于s(t)SNR的50%[15]。

由图1可知,天线组阵信号FSC方法中的两个关键技术分别为时延估计和时延补偿。时延估计算法主要通过对天线信号进行互相关、对互相关谱求反正切等运算实现。典型的时延估计算法有Simple、Sumple[16-17]、Eigen[18]等算法。在准确地估计出时延差和相位差后,就要进行高精度时延补偿,其主要目的是消除两路信号的时延差,将两路信号的时延与相位对齐,进而进行相干相加。因此,在估计性能达标的情况下,合成性能优劣取决于能否将估计所得的时延差和相位差高精度地补偿到各个天线。

1.2 典型时延补偿方法

文献[19-20]借鉴Sumple算法的思路,提出了一种以准合成输出信号作为虚拟参考信号的时延校准方法。该方法将待修正天线以外的其他所有天线的信号作为虚拟参考天线,提高了虚拟参考信号的SNR,从而有效提高了时延估计性能。然而,时域方法将信号以整体形式(全带宽)进行时延估计和补偿,存在两方面缺点:① 相关时,需要循环卷积,运算量大;② 补偿时,采用数字延迟线,只能进行整数时延补偿,补偿精度受采样率限制。美国航空航天局(National Aeronautics and Space Administration, NASA)深空网在其全频谱处理阵(full spectrum processor array, FSPA)设备中,使用了一种基于上下边带的残余时延和相位差联合估计方法[3,14,21]。该方法首先通过信号滤波器提取各天线信号的上边带和下边带,然后利用相位估计算法分别估计待校准天线与参考天线上下边带的相位差,最终两相位点构成的直线的斜率即为残余时延,截距即为载波相位差。该方法的优势在于运算量小,而且将时延估计问题转化为相位估计问题,在低SNR条件下,各边带可以采用高性能相位估计算法来提高估计精度。然而,该方法存在两个问题:① 由于相位估计算法只能提取初相差,当上下边带频率差较大或残余时延较大时,易出现模糊问题[22-23];② 时延补偿精度受采样率限制[24]。

由上述分析可知,时域合成方法均存在补偿精度受采样率限制的问题。即使假设时延估计误差为零,补偿后的小数时延也将导致频带内相位滑动,从而恶化合成性能[3,25-26]。尤其当带宽较大时,上述方法不再适用。因此,引入更合理的小数时延补偿方法是信号合成的重点和难点问题之一。

1.3 整数时延补偿

整数时延通常而言就是信号的采样点超前或滞后,现有的整数时延补偿方法通过移动信号采样点来实现。在现场可编程门阵列(field programmable gate array, FPGA)平台下,整数时延补偿可通过移位寄存器实现。在Matlab读数据处理的方式下,可通过移动读文件的起始地址实现整数时延补偿。

在相位差估计模块,需要在频域进行信号的共轭相乘、累加平均、求反正切等运算。其中,累加平均就是将M组512点(假设快速傅里叶变换(fast Fourier transform, FFT)点数为512)的频域信号进行能量累积(FFT积分),以提高估计的准确性。在FPGA平台下和Matlab仿真中,都能保证每次移动采样点后,有足够多的信号(大于等于积分长度M×512)以进行后续的处理。

考虑到GPU在实时处理时以信号数据块的方式进行传输,下面分析典型的整数时延补偿方法(移动信号采样点),以及以这种方式实现的可行性,及其存在的问题。在GPU平台下,要满足信号合成的实时性,就必须在特定时间内处理完成一定的数据量(例如在1 s之内完成与采样率数值大小一致的数据量),这就需要对数据流进行分块处理。图2所示为GPU数据流分块处理示意图。

图2 GPU数据流分块处理示意图Fig.2 Schematic diagram of GPU data flow block processing

每个数据块的大小固定为M×512,每次迭代通过cudaMemcpy分别将天线1和参考天线的一个数据块传入GPU进行运算。第1次迭代时,时延补偿初始化为0,因此整数时延与小数时延均为0,不需要对天线1和天线2进行采样点偏移。第2次迭代时,利用第1次迭代估计的时延值进行补偿,首先将时延取整得到整数时延。若天线1相比参考天线时延超前D个采样点,则天线1需要向前移动D个采样点以实现整数时延补偿,移动之后天线1只剩下(M×512-D)个有效数据。之后进行时延差估计,需要对天线1和参考天线做FFT运算。此时,参考天线有M×512个有效数据,而天线1只有(M×512-D)个有效数据。若FFT运算时点数不够,则需自动进行补零操作。因此,参与FFT运算的天线1信号并非完整的M×512数据点数,而是末尾补了D个0的数据块。同理,若天线2相比参考天线时延滞后D个采样点,则天线2需要向后移动D个采样点以实现整数时延补偿,移动之后天线2只剩(M×512-D)个有效数据。在FFT运算时同样需要进行补零操作,这就会导致时延差估计时无法利用所有数据点的信息,估计的时延差误差较大,进而无法实现高精度时延补偿。

1.4 小数时延补偿

宽带信号时域合成方法都采用整数时钟移位的时延补偿方法,存在时延补偿精度低的问题。带宽越大,时延补偿精度要求越高。为保证合成损失小于0.1 dB,残余时延引起的整带内的相位差必须小于20°。若带宽为500 MHz,则残余时延必须小于0.11 ns。设采样时钟为1 280 MHz,该补偿方法的补偿精度为0.39 ns(半个时钟周期),已不能满足要求,必须采用更高精度的小数时钟时延补偿方法。

小数时延就是时延数值中的小数部分,而小数时延无法通过移动信号的采样点实现,因此需要寻找其他方法进行小数时延补偿[27]。常见的小数时延补偿主要分为两类,分别是时域补偿和频域补偿。二者的主要区别在于是否在频域进行小数时延补偿。在FPGA平台下,时域补偿法主要通过各种最小误差准则逼近理想系统获得有限冲击响应,主要包括基于最小均方误差(minimum mean square error, MMSE)准则滤波法、拉格朗日插值法和基于Farrow结构的滤波器组方法等[27]。而分数时延数字滤波器大大增加了硬件开销和实现的复杂度。

1.5 小 结

现有时延补偿方法的不足主要体现在以下几个方面。

(1) 在GPU平台下,为了实现实时处理,每次处理的数据块的大小都是固定的。而整数时延补偿通过移动信号的起始采样点来实现,这将导致数据块的有效点数减少,在之后的FFT运算时会自动进行补零操作,从而使得估计时延差时没有充分利用所有的数据,导致时延差估计的精度降低,无法实现高精度时延补偿。

(2) 时域小数时延补偿通常采用分数时延数字滤波器,而这种方法的实现复杂度高且增加了硬件开销,实现信号的实时处理难度较大。

2 基于GPU的天线组阵信号时延补偿方法

2.1 总体方案

本文对基于GPU的时延补偿方法展开研究,图3为基于GPU的天线组阵信号时延补偿方法的总体方案框图。N个天线信号经采集卡输出为N路并行的数字信号,其中某个天线固定为参考天线。首先,进行整数时延补偿,之后对所有天线信号进行子带拆分,此时信号已转为频域,之后进行小数时延补偿和相位补偿。补偿完成后,将信号分别传输至时延差估计模块和子带合成模块。时延差估计模块赋值计算出天线间的时延差和相位差,并将待补偿的值传输至下一次迭代中。子带合成模块负责将天线信号合成并输出至子带重构模块,进而输出合成信号。

图3 基于GPU的天线组阵信号时延补偿方法总体方案框图Fig.3 Block diagram of the overall scheme of time delay compensation method of antenna array signal based on GPU

2.2 整数时延补偿

2.2.1 天线滞后参考天线

在整数时延补偿方面,依旧采用移动信号采样点的方法实现。针对数据块的有效数据点数不足和进行FFT时自动补零的问题,采用数据块重叠保留的思想进行改进。图4为天线滞后参考天线时的整数时延补偿示意图,具体实现步骤如下。

图4 天线滞后参考天线时整数时延补偿示意图Fig.4 Schematic diagram of integer time delay compensation when the antenna lags behind the reference antenna

步骤 1第1次迭代开始,参考天线第1个数据块A1(M×512个数据)和天线X的第1个数据块B1,通过PCIE总线由CPU内存传输到GPU片上内存。在这两个数据块前分别添加1个长度为N、数值为0的数据块,并将后续处理的地址指向数据块的最前端(补0数据块的首地址),然后开始时延补偿。由于初始化时延补偿值为0,因此整数时延与小数时延均为0,此次迭代不需要进行整数时延和小数时延补偿,FFT运算的指针不需要偏移,仍为整个数据块的最前端。FFT需要的数据点数为M×512,因此天线1和参考天线的数据块的末尾N个数据未参与本次计算。之后进行时延估计,假设天线X(B1数据块)滞后参考天线(A1数据块)D1个采样点,则时延估计后的整数时延为D1。将参考天线数据块末尾N个数据组成数据块A1_tail,将天线X数据块末尾(D1+N)个数据组成数据块B1_tail,将A1_tail、B1_tail数据块拷贝至下一个积分区间。

步骤 2第2次迭代开始,参考天线第2个数据块A2(M×512个数据)和天线X的第2个数据块B2通过符合总线和接口标准(peripheral component interface express, PCIE)总线由CPU内存传输到GPU片上内存。将上一个积分区间拷贝而来的A1_tail添加至A2的前端构成A2_new,将B1_tail添加至B2的前端构成B2_new,并将后续处理的地址指向A2_new、B2_new数据块的最前端。A1_tail为A1末尾的N个数据,B1_tail为B1数据块末尾的(D1+N)个数据,此时B2_new(天线X)超前A2_new(参考天线)D1个采样点,实现了天线X的整数时延补偿。同时,保证了数据的连续性,在之后的FFT运算时数据点数大于M×512,不需要进行自动补零。该方法在后续估计时延差时充分利用了所有的数据,提高了估计的精度。假设天线X(B2_new数据块)滞后参考天线(A2_new数据块)D2个采样点,则时延估计后的整数时延为D2。将参考天线数据块(A2_new)末尾的N个数据组成数据块A2_tail,将天线X数据块(B2_new)末尾的(D2+D1+N)个数据组成数据块B2_tail,将A2_tail、B2_tail数据块拷贝至下一个积分区间。

步骤 3第3次迭代,之后每次迭代与第2次迭代的处理过程相同。

2.2.2 天线超前参考天线

天线超前参考天线时的处理方法与滞后参考天线时的处理方法类似。图5为天线超前参考天线时的整数时延补偿示意图。

图5 天线超前参考天线时整数时延补偿示意图Fig.5 Schematic diagram of integer time delay compensation when the antenna is ahead of the reference antenna

步骤 1第1次迭代开始,参考天线第1个数据块A1(M×512个数据)和天线X的第1个数据块B1通过PCIE总线由CPU内存传输到GPU片上内存。在这两个数据块前分别添加1个长度为N、数值为0的数据块,并将后续处理的地址指向数据块的最前端(补0数据块的首地址),然后开始时延补偿。由于初始化时延补偿值为0,因此整数时延与小数时延均为0,此次迭代不需要进行整数时延和小数时延补偿,FFT运算的指针不需要偏移,仍为整个数据块的最前端。FFT需要的数据点数为M×512,因此天线1和参考天线的数据块的末尾N个数据未参与本次计算。之后进行时延估计,假设天线X(B1数据块)超前参考天线(A1数据块)D1个采样点,则时延估计后的整数时延为-D1。将参考天线数据块末尾N个数据组成数据块A1_tail,将天线X数据块末尾(-D1+N)个数据组成数据块B1_tail,将A1_tail、B1_tail数据块拷贝至下一个积分区间。

步骤 2第2次迭代开始,参考天线第2个数据块A2(M×512个数据)和天线X的第2个数据块B2通过PCIE总线由CPU内存传输到GPU片上内存。将上一个积分区间拷贝而来的A1_tail添加至A2的前端构成A2_new,将B1_tail添加至B2的前端构成B2_new,并将后续处理的地址指向A2_new、B2_new数据块的最前端。A1_tail为A1末尾的N个数据,B1_tail为B1数据块末尾的(-D1+N)个数据,此时B2_new(天线X)滞后A2_new(参考天线)D1个采样点,实现了天线X的整数时延补偿。同时保证了数据的连续性,在之后的FFT运算时数据点数大于M×512,不需要进行自动补零。该方法在后续估计时延差时充分利用了所有的数据,提高了估计的精度。假设天线X(B2_new数据块)超前参考天线(A2_new数据块)D2个采样点,则时延估计后的整数时延为-D2。将参考天线数据块的(A2_new)末尾N个数据组成数据块A2_tail,将天线X数据块(B2_new)的末尾(-D2-D1+N)个数据组成数据块B2_tail,将A2_tail、B2_tail数据块拷贝至下一个积分区间。

步骤 3第3次迭代,之后每次迭代与第2次迭代的处理过程相同。

2.3 小数时延与残余相位补偿

小数时延补偿若采用可调分数时延数字滤波器,则会增加硬件开销和实现复杂度,信号实时处理的实现难度较大。而将信号转为频域,通过频域进行补偿[28-30]可以有效解决上述问题。

首先,将宽带信号拆分成多个子带[31-32],子带间隔决定了最大无模糊时延。例如,当采样率为1 280 MHz,子带数为256时,子带间隔为5 MHz,则最大无模糊时延为200 ns,大大减小了系统标校的精度要求。其次,频域合成方法[33-34]残余的小数时延以及相位在频域进行补偿,通过对各子带进行线性相位偏移来实现。这样,由残余小数时延引起的整带内相位滑动被限制在子带范围内,大大减小了小数时延引起的合成损失。仍以上个例子进行说明,残余小数时延最大值为0.39 ns(半个时钟周期),在500 MHz带宽内引起的相位差约为70°,而在5 MHz子带内引起的相位差仅为0.7°,其引起的合成损失基本可以忽略。此外,频域合成方法[35-36]通过对所有子带相位差进行线性最小二乘拟合,可以利用所有子带的相位差信息,因此其残余时延和相位的估计精度也更高。

因此,在小数时延补偿方面,本文采用频域补偿的方法。在频域对子带分别进行补偿主要有以下优势:① 相比在全带宽进行小数时延补偿,通过将各子带中心频率独立进行相位对齐,可将由小数时延引起的整带内相位滑动限制在子带范围内,大大减小了小数时延引起的合成损失;② 相比时域小数时延补偿,具有结构简单、运算量小的优势。在频域进行小数时延补偿,采用线性相位偏移实现,对各个子带独立进行相位偏移,可使用GPU并发进行加速,大大提高了小数时延补偿的实时性。

3 基于GPU的天线组阵信号时延补偿方法

3.1 实现流程

图6为基于GPU的时延补偿方法流程图。初始化时延和相位补偿值为0,每次迭代过程先对信号进行补偿,再对残余时延和残余相位进行估计,最后对时延和相位补偿值进行更新。其中,delay_now和phase_now为当前时刻的残余时延和残余相位的估计值,mu为调整步长。因此,在每次迭代过程中,时延和相位补偿值都由上次迭代过程估计得出,通过闭环反馈支路进行更新。也就是说,前一个数据块估计出的残余时延与残余相位都为下一个数据块的时延和相位的补偿值进行了预报。

图6 基于GPU的天线阻阵时延补偿方法流程图Fig.6 Flowchart of time delay compensation method of antenna array based on GPU

首先利用上一次迭代估计出的残余时延计算出整数时延和小数时延;然后使用基于数据块重叠保留的方法进行整数时延补偿;之后利用小数时延和残余相位,通过多项式求解函数ployval反推出各个子带需要补偿的相位值。然后,通过线性相位偏移进行小数时延和残余相位补偿。

基于GPU的天线组阵时延补偿方法实现流程图如图7所示。

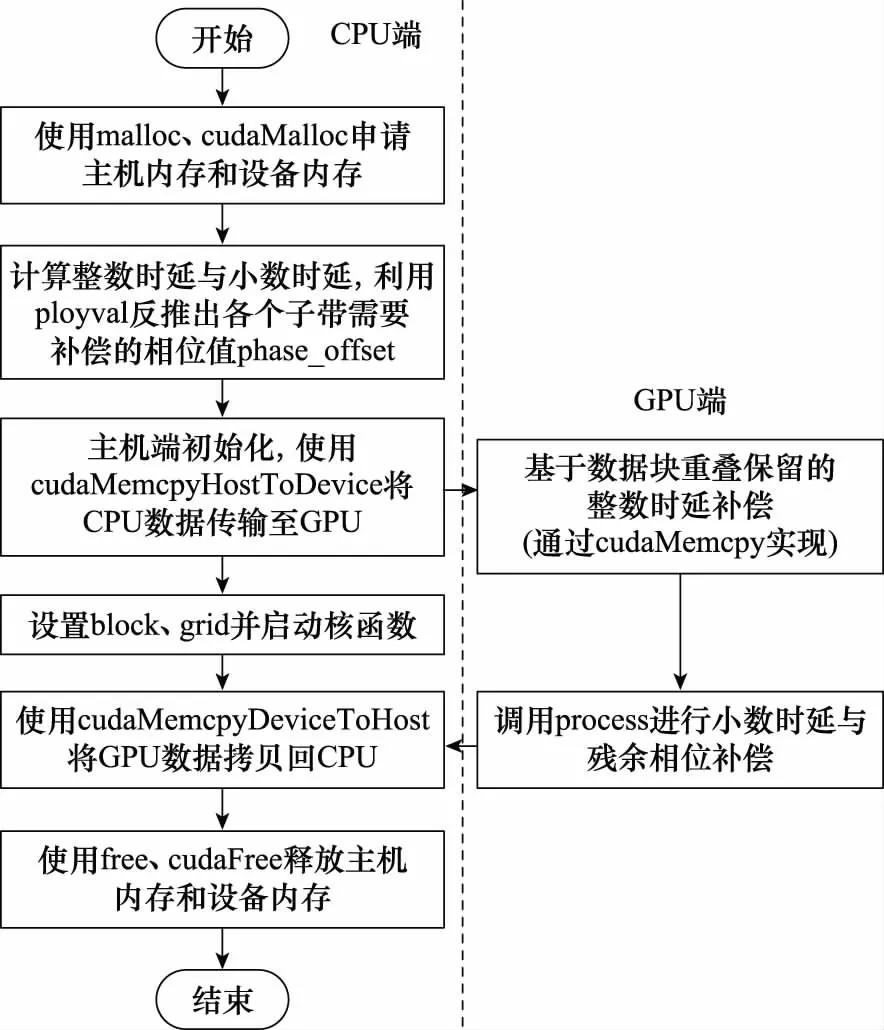
图7 基于GPU的天线组阵时延补偿方法实现流程Fig.7 Implementation process of GPU-based antenna array time delay compensation method

本文设计的基于GPU的天线组阵信号时延补偿方法基于GPU+CPU异构处理平台开发,以CPU为控制器,以GPU为协处理器。由于GPU采用并行处理的架构设计,其在进行大量并行数据处理时计算性能明显优于CPU[37]。

3.2 时延补偿算法GPU实现

根据第2.2节对算法的具体描述,本文设计的整数时延补偿的CUDA代码如算法1所示,主要通过使用CUDA中的数据传输函数cudaMemcpyDeviceToDevice实现。delay为上一次迭代估计出的时延补偿值,step为当前已迭代次数。signal为本次迭代由CPU传至GPU内存中的初始数据块,signal_last为上一次迭代参与运算的数据块,signal_now为本次迭代待参与运算的数据块。N为重叠保留数据块初始化大小,参与运算数据块的大小固定为nsize,其中参考天线数据块命名均以ref结尾。

算法 1 基于数据块重叠保留的整数时延补偿输入: delay、step、signal、signal_last、N、nsize输出: signal_nowInteger_delay=int (round (delay [step-1]));cudaMemcpy(signal_now, signal_last+(nsize-N)-Integer_delay, (N+Integer_delay)×sizeof(float2), cudaMemcpyDeviceToDevice);cudaMemcpy(signal_now_ref, signal_last_ref+(nsize-N), N×sizeof(float2), cudaMemcpyDeviceToDevice);cudaMemcpy(signal_now+(N+Integer_delay), signal, (nsize-(N+Integer_delay))×sizeof(float2), cudaMem-cpyDeviceToDevice);cudaMemcpy(signal_now_ref+N, signal_ref, (nsize-N)×sizeof(float2), cudaMemcpyDeviceToDevice)

步骤 1使用取整函数计算整数时延;

步骤 2将上一次迭代参与运算的数据块(signal_last)末尾的(N+Integer_delay)个数据拷贝至signal_now的首地址处;

步骤 3将signal拷贝至signal_now的(N+Integer_delay)地址处。

线性相位偏移函数如算法2所示,rec为待处理数据,dst为已处理数据。phase为相位偏移值,处理数据长度为length。

算法 2 线性相位偏移函数输入: rec、phase、length 输出: dst__global__ void process(float2×rec, float×phase, float2×dst, int length){int tid=threadIdx.x+blockIdx.x×blockDim.x;if (tid>=length)return;float Phase=phase[tid% NFFT];dst[tid].x=rec[tid].x×cos(Phase)+rec[tid].y×sin(Phase);dst[tid].y=-rec[tid].x×sin(Phase)+rec[tid].y×cos(Phase);}

小数时延与残余相位补偿如算法3所示。delay、phase分别为上一次迭代估计出的时延补偿值、相位补偿值,采样率为Fre_sample,当前已迭代次数为step,子带频率范围为f_span,FFT点数为NFFT,参与运算数据块大小固定为nsize。signal_FFT为待补偿的频域信号,补偿完成的频域信号为signal_process。

步骤 1计算小数时延fraction_delay;

步骤 2以fraction_delay和phase为输入,利用ployval反推出各个子带需要补偿的相位值phase_offset;

步骤 3调用process函数对转至频域的信号signal_FFT进行线性相位偏移,即小数时延与残余相位补偿。

4 实验验证与分析

4.1 系统及核心参数设计

利用相位校正(phase calibration, PCAL)信号进行性能分析,PCAL信号的频率特性具有梳状频谱特性和线性相位特性。通过在接收机链路输出端提取PCAL信号的自相位谱,可以得到PCAL信号经过整个传输链路的附加时延、相位以及非线性相位失真。

选用表1和表2所示的GPU和CPU仿真平台和具体仿真环境参数,仿真参数设置如表3所示。

表1 GPU参数

表2 CPU参数

表3 仿真实验参数

本文中所有幅度均为仿真信号的归一化幅度。图8所示为时延补偿结果对比图。图8(a)为天线1与参考天线初始信号的时域波形细节图(为方便比较,选取其中一段数据)。从图8(a)可以看出,天线1与参考天线的时延为2个采样点,信号未对齐。图8(b)为现有方法(即FFT时点数不够的自动补零方法)迭代30次时的补偿细节图,图8(c)为本文提出的基于数据块重叠保留的整数时延补偿迭代30次时的补偿细节图。从图8(b)和图8(c)可以看出,两种方法的天线1与参考天线都实现了对齐,且合成信号的幅度约为参考天线的2倍。从时域波形无法看出二者之间的区别。

图8 时延补偿结果对比图Fig.8 Comparison diagram of time delay compensation results

图9为时延补偿误差对比图,即迭代第30次时两种方法的补偿误差(天线1补偿后信号幅度与参考天线之差)对比图,现有方法的补偿误差在10-1量级,而本文方法的补偿误差在10-7量级。

图9 时延补偿误差对比图Fig.9 Time delay compensation error comparison chart

图10为两种方法的时延补偿值随迭代次数变化的曲线。delayi=delayi-1+mu×delaynow,其中delaynow为本次迭代计算出的时延,delayi-1为上一次迭代时的时延补偿值,delayi为本次更新后的时延补偿值。在时延真值为2个采样点的情况下,20次迭代后,两种方法的时延补偿值都收敛于某一值。本文方法的时延补偿值收敛于真值2.000,现有方法的时延补偿值收敛于2.003。这是由于FFT自动补零导致参与运算的有效数据点数减少,导致时延差估计的精度降低,无法实现高精度时延估计与补偿。

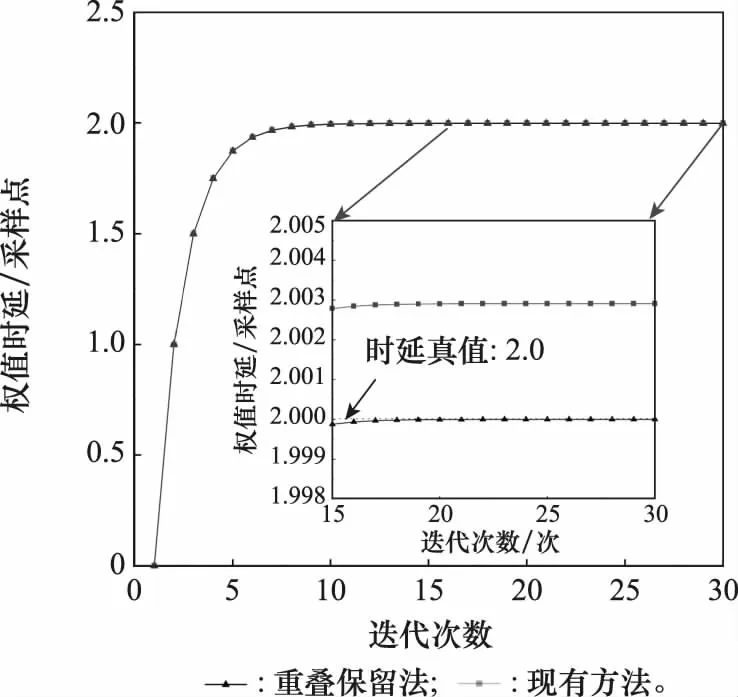
图10 时延补偿值对比图Fig.10 Time delay compensation value comparison

在得到所有子带的相位差后,需要利用线性最小二乘拟合方法来估计宽带信号的残余时延和相位。拟合直线的斜率即为残余时延,截距即为零频处的残余相位。因此,拟合的精度直接影响估计的残余时延和相位的精度,进而影响补偿对齐的精度。下面分析、对比两种方法在最小二乘拟合时的残差。

图11为第1次迭代拟合残差对比图,图11 (a)为现有方法的第1次迭代拟合残差,拟合残差为10-12量级。由于初始时延补偿值为0,因此不需要进行整数时延补偿,在FFT时也不需要进行补零操作,充分利用了所有信号数据,因此其拟合残差很小,拟合性能好。本文提出的方法如图11(b)所示。在第1次迭代时,拟合残差达10-5量级。由于初始化进行了信号补零,导致第一次迭代时没有充分利用所有信号数据,拟合残差较大。

图11 第1次迭代拟合残差对比图Fig.11 Comparison of the first iteration fitting residual

图12为第30次迭代(收敛时)的拟合残差对比图。现有方法除第1次迭代,拟合残差均达到了10-5量级。由于未进行数据的重叠保留处理,在FFT时需要进行补零操作,因此其拟合残差较大,拟合质量差。而本文提出的方法在第1次迭代之后,拟合残差为10-10量级。由于拟合前的数据连续且充分,拟合残差小,拟合质量高。

图12 第30次迭代拟合残差对比图Fig.12 Comparison of the 30th iteration fitting residual

4.2 加速效果验证与分析

利用NVIDIA提供的分析工具NVIDIA Nsight Systems软件[37]详细分析了算法运行过程中各模块的耗时情况,算法运行时序图如图13所示。

图13 算法运行时序图Fig.13 Algorithm runtime diagram

之后对1 000次迭代的耗时进行记录,并取平均值,得到算法在GPU端运算与CPU端运算两部分的具体耗时,如表4所示。其中,GPU端运算占55%,CPU端运算占45%,GPU端耗时略多于CPU端。之后对GPU端总耗时中数据传输与核函数实际执行时间的占比进行分析,数据传输包括三个方向:CPU到GPU;GPU到CPU;GPU到GPU。也即MemcpyHtoD、MemcpyDtoH、MemcpyDtoD,分析结果如表5和图14所示。

表4 算法耗时对比表

表5 GPU端耗时对比表

图14 GPU端耗时对比饼图Fig.14 Time consumed comparison pie chart of GPU

由表5可以看出,在GPU端总耗时中,核函数实际执行时间占总耗时的45.13%,数据传输时间占总耗时的54.87%。可见,数据传输时间占比稍多于核函数实际执行时间占比,因此算法还可通过GPU异步流并发的方式进行进一步优化,隐藏部分数据传输耗时,使核函数实际执行的时间占比进一步提高。

为了进一步研究时延补偿模块及整个系统的耗时情况,针对1 s的数据进行加速比分析和实时性分析。图15为时延补偿加速对比图,其中,本文设计的基于GPU的时延补偿方法模块处理完成1 s的数据量共耗时约为6.2 ms。

图15 时延补偿加速对比图Fig.15 Comparison chart of time delay compensation acceleration

CPU串行时延补偿与并行算法的区别主要有两点:其一在于整数时延补偿的方式,串行方法采用memcpy函数在CPU端进行,并行算法采用cudaMemcpyDtoD函数进行传输;其二在于串行方法的小数时延与相位补偿没有进行并行优化,需要从头至尾遍历每一个值并乘以补偿的相位。在处理相同数据量时耗时114 ms,加速比约为18。

图16为信号合成实时性对比图。在信号合成系统中,分别采用基于GPU的时延补偿方法和CPU串行时延补偿方法。除时延补偿,其余模块的处理方式相同。对比两种方法在合成1 s数据的耗时可以看出,采用GPU的时延补偿方法耗时约783 ms,采用CPU串行时延补偿方法耗时约9 105 ms。实时性的要求是,处理1 s的数据耗时少于1 s (1 000 ms)。因此,本文基于GPU的时延补偿方法在被应用于合成系统中时达到了实时处理的能力,而在被应用于现有的CPU串行时延补偿方法的合成系统时远未达到实时性,只能应用先采集数据、之后进行非实时处理的方式。

图16 信号合成实时性对比图Fig.16 Comparison chart of signal synthesis real-time property

最后,对访存带宽需求进行了分析,利用NVIDIA-smi命令监视算法对GPU访存的需求。从图17可以看出,GPU的内存总共约为80 GB,在文中表1的各项参数下,GPU已占用约为1.2 GB,该数值对相关的仿真实验有一定的参考价值。

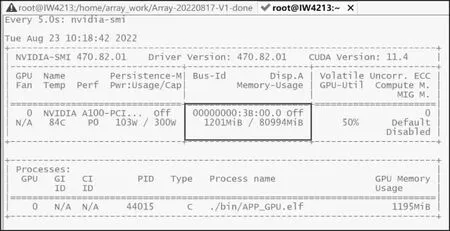
图17 NVIDIA-smi命令监视窗口Fig.17 NVIDIA-smi command watching window

5 结 论

针对大规模天线组阵合成系统天线数量越来越多、接收信号的带宽越来越大,单独使用CPU已不能满足运算需求这一问题,本文研究了基于GPU的天线组阵信号时延补偿方法,分析了算法并行的可行性,并设计了基于GPU的天线组阵信号时延补偿方法,通过仿真对比实验验证了本文提出的并行算法的优越性。本文所做主要工作如下。

(1) 针对GPU平台以数据块为单位进行处理的方式,本文首先分析了典型的整数时延补偿方法在GPU平台实现的可行性,发现将现有方法直接应用于GPU无法保证正确性。在此基础上,设计了基于数据块重叠保留的整数时延补偿方法。

(2) 分析了传统小数时延方法的优劣,并设计了适合于GPU并行优化的频域小数时延补偿方法。

(3) 通过实测数据对基于GPU的天线组阵信号时延补偿方法进行了实验验证。首先验证了算法的正确性,证实了本文方法的补偿误差远低于现有的补偿方法,在无噪声的情况下达到10-7量级,证明了本文方法在GPU平台上实现的正确性。之后,对基于GPU的天线组阵信号时延补偿方法和CPU串行时延补偿方法的实时处理性能进行了对比。实验表明,本文方法相比CPU串行方法有约18倍的加速比,利用本文方法可以实时地进行信号合成。

本文的并行算法可以运用到未来的大规模天线组阵信号合成系统中,实现高速、准确、实时的信号合成,有力支持未来的一系列深空探测任务。